氣死!又被數據騙了!
最近發現,公司有的新人喜歡在做數據分析報告的時候做一些小手腳,有時候差點連我都被唬住了,今天就來和大家聊聊數據分析里的那些騙人把戲。
做數據分析的人做的久了,就會自然而然產生一種想法,認為數據展示出來的東西一定是正確的。畢竟如果連我們自己都質疑數據分析的權威性和說服力,那我們數據分析人的工作不就成了白費功夫了嘛。
一開始,我也認為這是一條不可撼動的“鐵律”,但是漸漸我開始發現,數據分析很難做到一絲不茍地嚴謹,也很難做到完全正確,有時候甚至會誤導我們的判斷。
因為數據不僅能夠揭露事實,它也可以用來隱藏真相!
比如下面這三種騙局,就是利用了數據的欺瞞性,變成了很容易讓人上當的鬼把戲!
坐標軸里做手腳
可視化圖表本來是為了能夠讓人更加直觀、方便、快捷地了解數據情況,包括數據的異常情況和發展趨勢,所以公司的老板和領導都喜歡看圖表,覺得圖表總不會騙人吧?但是可視化圖表有一個很大的局限性,就是必須保證指標的統一性。而很多人恰恰利用了指標的不一致性,或是增加某些東西,或是隱藏某些東西,就可以讓圖表說謊。
1、橫坐標作弊:讓數據更“平穩”
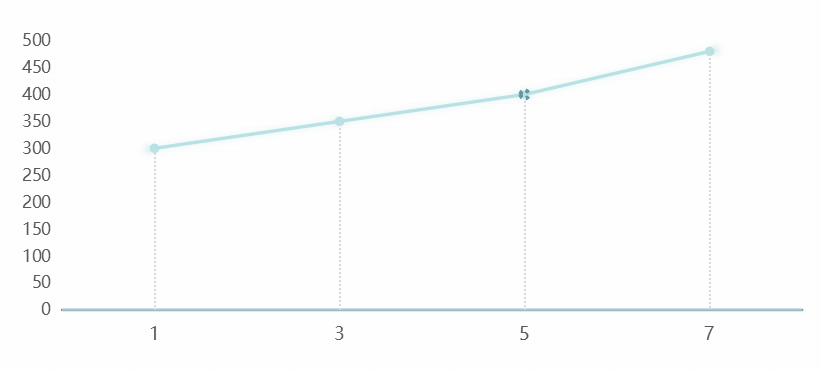
如果你是一位投資人,看到了上圖這樣一份公司近幾年的財務報告,展示了公司每年凈利潤的走勢,你就會覺得:哇,這家公司經營的不錯啊,每年都在增長,看起來很有投資價值!
但是如果你是一個比較善于觀察的人,你就會發現一個問題:橫坐標軸只有奇數列!
這就是很多人都會玩的一種把戲,故意刪減掉一些影響整體趨勢的值,為了讓整個數據更加平滑、平穩,就會直接將坐標軸列刪除,美名其曰“數據太多、分組展示。”
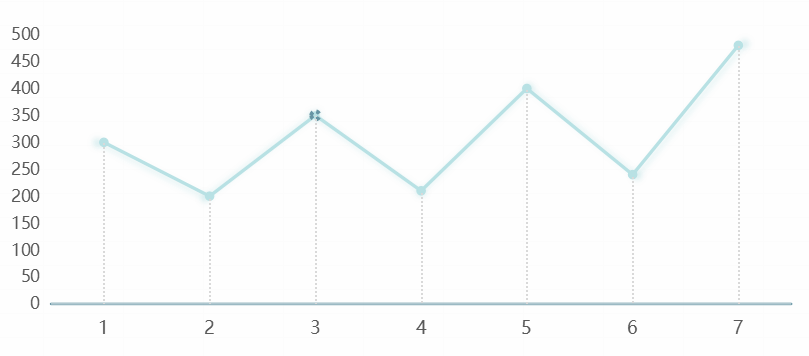
而實際上,我們將橫坐標軸進行還原,這家公司的財務報告就可能變成下圖這個樣子:
財務數據波動如此劇烈,估計每個投資人都不敢給這家公司一分錢了吧!
2、縱坐標作弊:讓數據更“懸殊”
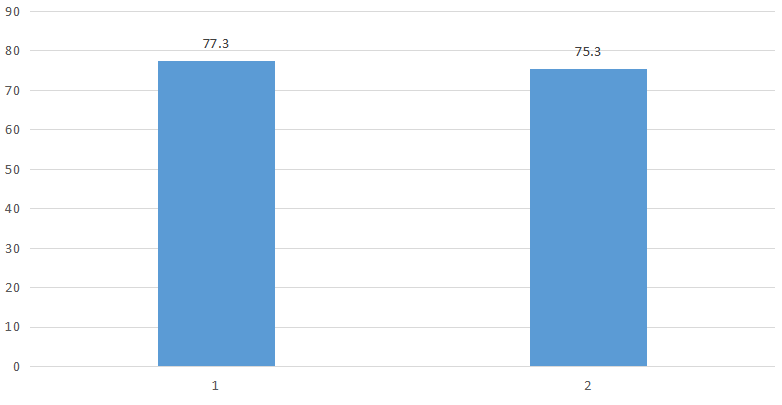
我們經常可以在電視中看到這樣的統計分析圖,用來展示某個屬性或者指標的對比情況。
比如這位棒球選手的速度,直觀上給人的感覺好像是下降了非常多,但是我們如果看到柱狀圖上的數據之后,就會發現根本就是從77.3下降到了75.3而已。
其實跟上一種把戲一樣,這個騙局就是將縱坐標軸“處理”了一下,縱坐標軸不再是從0開始,而是從某個值開始,這樣就會將兩者之間的差異進行放大,會讓我們覺得數據十分的懸殊。
而實際上,我們將縱坐標的起點還原為0之后就會發現,其實二者的差距非常小。
當然這種把戲玩得最好的,還要說是美國的媒體,用這種方式去抨擊領導人或者是贊揚領導人可以說是屢試不爽!
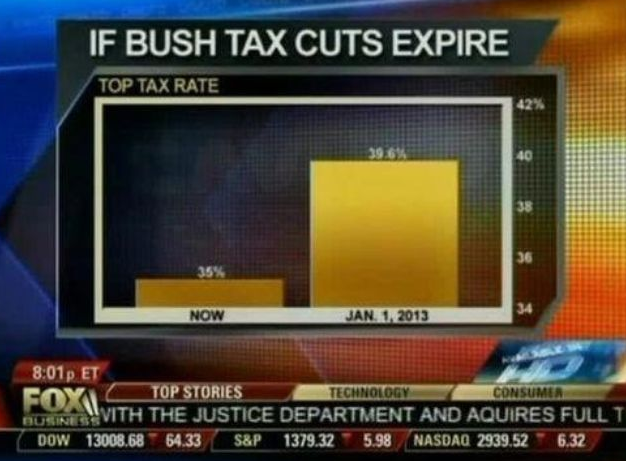
3、整體比例作弊:讓數據更“突出”
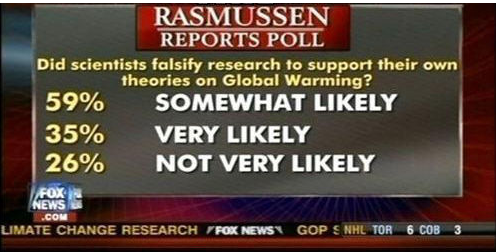
如果大家覺得不用坐標圖,不就可以避免橫縱坐標軸的作弊行為了嗎?那你可就想的太簡單了,因為這一招更加高明!當然這招還是美國媒體玩的最好,比如下面這份統計數據,最高與最低差了33%的比例,可以說非常懸殊。
但是其實我們很容易發現,這三個數值加起來的比例根本不是100%,而是120%!也就是說統計者人為地將整體數據設置為了120%,因為展示的是比例關系,因此這種比例就會擴大,實際上兩者之間的差距僅僅只有28%!
偽相關
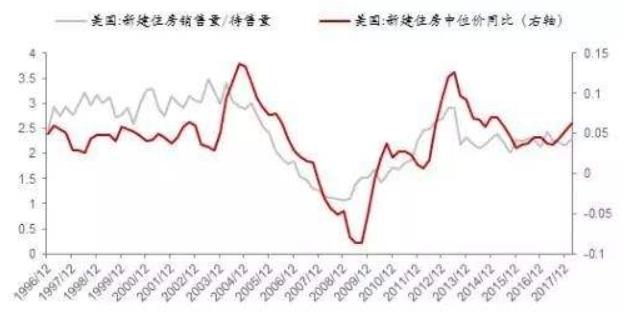
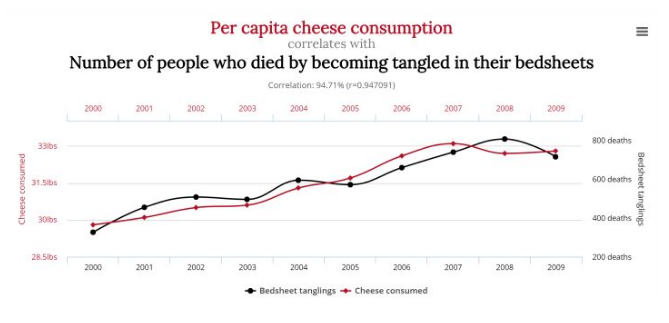
比起第一種把戲,這種把戲沒有在可視化圖表上動手腳,而是利用了大家對于相關性的誤解,認為相同即是相關。比如說下面這兩張圖,第一張圖是美國新建住房的銷售量與新建住房價格之間的關系走勢圖,第二張圖是美國每年的芝士消費量與每年被床單纏住窒息而死的人數之間的關系走勢圖。
我們能夠看出來兩張圖都呈現出了高度的擬合性,那么我們能說兩種圖里的因素都具有很高的相關性嗎?
首先,第一張我們應該都沒有什么質疑,因為房價與銷售量之間存在很強的因果關系,所以兩者的變化趨勢基本都是一致的;
但是第二張中雖然兩個因素的變化趨勢也是一致的,但是我們很難相信,一個國家的芝士消費量,會與每年被被單纏住窒息的死亡人數有關系,因為這兩者之間很難產生因果關系,這就叫做“偽相關”。
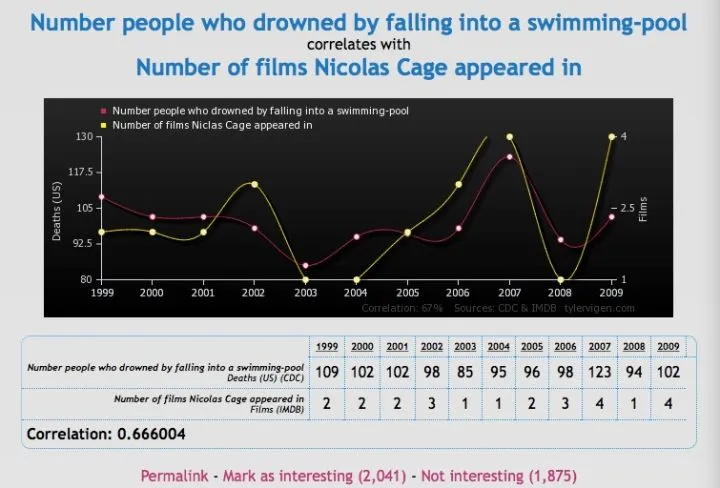
類似的例子還有很多,比如尼古拉斯凱奇在電影中的出鏡次數和淹死在游泳池里的人數:
邏輯誤導
邏輯誤導經常出現在我們在進行演繹推理的時候,比如最常見的邏輯誤導就是以偏概全,通過根據群體中一小部分人的經歷得出有關整個群體的結論。
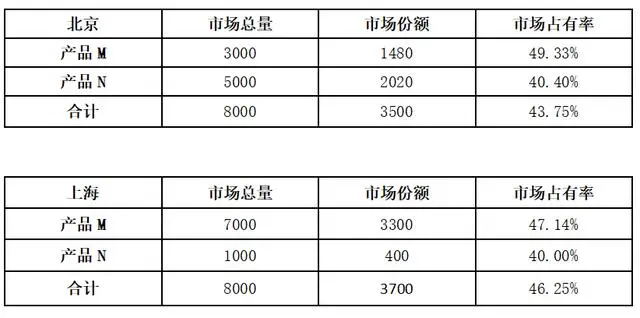
比如,你是一家集團公司的總裁,在北京和上海均有業務,你要根據市場占有率情況進行重大的戰略調整。兩地的市場占有率如下表。
所以,你會判斷上海市場的業務要優于北京市場的,對么?
此時,只考慮了地區的差異,把所有的數據看成了整體,看似確實是上海市場的業務優于北京市場。
但如果考慮多因素分析,根據各項業務實際占有率,你會驚奇地發現:產品M的市場占有率,北京(49.33%)高于上海(47.13%),產品N的市場占有率,北京(40.4%)也同樣高于上海(40%)。
北京的每一項業務都比上海要好!
所以,面對數據,我們一定要秉持著絕對客觀、嚴謹的態度去看待,做數據分析,是為了推動業務的發展,挖掘更多價值,而不是為了迎合業務想要的結果。
諸位共勉!