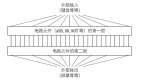
動物與人類的關鍵學習期,深度神經網絡也有
0 引言
我們這篇文章討論的問題是根據 ICLR 2019 中的一篇文章而來:《CRITICAL LEARNING PERIODS IN DEEP NETWORKS》[1]。在這篇文章中,作者提出了這樣一個概念:對于深度神經網絡來說,與動物和人類的學習過程類似,其對于技能的學習過程也存在一個“關鍵學習期”。從生物學角度來看,關鍵期(critical periods)是指出生后早期發育的時間窗口,在這期間,感知缺陷可能導致永久性的技能損傷。生物學領域的研究人員已經發現并記錄了影響一系列物種和系統的關鍵期,包括小貓的視力、鳥類的歌曲學習等等。對于人類來說,在視覺發育的關鍵時期,未被矯正的眼睛缺陷(如斜視、白內障)會導致 1/50 的成人弱視。
生物學領域的研究人員已經確定,人類或動物存在關鍵期的原因是對神經元可塑性窗口的生物化學調控(the biochemical modulation of windows of neuronal plasticity)[2]。神經網絡最早起源就是期望模擬人腦神經元的工作模式,Achille 等在文獻 [1] 中證明了深度神經網絡對感覺缺陷的反應方式與在人類和動物模型中觀察到的類似。在動物模型中最終造成的損害的程度取決于缺陷窗口的開始(onset)和長度(length),而在神經網絡中則取決于神經網絡的大小。不過,在神經網絡中,缺陷并不會影響低層次的統計特征,如圖像的垂直翻轉,同時對性能并沒有持久的影響,以及最終可以通過進一步的訓練來克服。這一研究發現引發了作者的思考,他認為,深度神經網絡學習中存在的 “關鍵期” 可能來自于信息處理,而不是生化現象[1]。這一發現最終引發了本文所討論的問題,即 DNNs 中的關鍵學習期現象。
與此類似,我們也看到了其它一些討論相關問題的文章。當然,這些文章并沒有從 “關鍵期” 的角度來討論這個問題,只不過其所揭示的規律與 [1] 中關于 DNNs 中的關鍵期現象的規律非常相似,主要探討的是深度神經網絡訓練早期階段的問題,即在深度神經網絡的訓練過程中,早期階段與其它階段具有不同的“特點”。由于這些研究能夠從另外的角度證實 DNNs 中存在“關鍵學習期”,所以我們也將它們納入到本文的討論中。
例如,來自紐約大學等多家大學和研究機構的研究人員的工作《The Break-Even Point on Optimization Trajectories of Deep Neural Networks》[5],提出了一種模擬 DNNs 早期訓練軌跡的簡化模型。作者表示,損失面的局部曲率(Hessian 的頻譜范數)沿 DNNs 優化軌跡單調地增加或減少。梯度下降在 DNNs 訓練早期階段會最終達到一個點,在這個點上梯度下降會沿著損失面的最彎曲方向振動,這一點稱為損益平衡點(break-even point)。此外,來自 Princeton 大學和 Google 大腦團隊的研究人員發表的《The Surprising Simplicity of the Early-Time Learning Dynamics of Neural Networks》[4]指出,可以通過訓練一個簡單模型來模仿雙層全連接神經網絡早期學習階段的梯度下降動態變化。當只訓練第一層時,這個簡單的模型是輸入特征的線性函數;當訓練第二層或兩層時,它是特征和其 L2-norm 的線性函數。這一結果意味著,神經網絡直到訓練后期才會完全發揮其非線性能力。最后一篇文章發表在 PLOS COMPUTATIONAL BIOLOGY 中,提出了一個模仿人類視覺系統行為的前饋卷積網絡,作者具體分析了分析了不同層次的網絡表征("virtual fMRI"),并研究了網絡容量(即單元數量)對內部表征的影響。
1 深度網絡中的關鍵學習期 [1]

1.1 問題闡述
一個非常著名的影響人類的關鍵期缺陷的示例是人類在嬰兒期或兒童期白內障引起的弱視(一只眼睛的視力下降)[6]。即使在手術矯正白內障后,患者恢復患眼正常視力的能力也取決于視力缺陷的持續時間和發病年齡,早期和長期的視力缺陷會造成更嚴重的影響。本文的的目標是研究 DNN 中類似缺陷的影響。為此,作者訓練了一個標準的 All-CNN 架構,對 CIFAR-10 數據庫中的 32x32 大小圖像中的物體進行分類。實驗中使用 SGD 進行訓練。為了模擬白內障的影響,在最初的 t_0 個 epoch 中,數據庫中的圖像被下采樣為 8x8 大小,然后使用雙線性插值上采樣為 32x32 大小以得到模糊處理的圖像,破壞了小尺度圖像細節。之后,繼續訓練 160 個 epoch 以確保網絡收斂,并確保它能夠得到與對照組(t_0=0)實驗中相同數量的未損壞的圖像。
圖 1 給出了受缺陷影響的網絡的最終性能,具體的,將該性能展示為糾正缺陷 epoch t_0 的函數。我們可以很容易地從圖 1 中觀察到一個關鍵時期的存在。如果在最初的 40-60 個 epoch 中沒有去除模糊,那么與基線方法相比,最終的性能會嚴重下降(誤差最多會增加三倍)。這種性能的下降遵循在動物身上普遍觀察到的趨勢,例如早期研究中證實的在小貓出生后被剝奪單眼的情況下觀察到的視覺敏銳度的損失與缺陷的長度有關[7]。
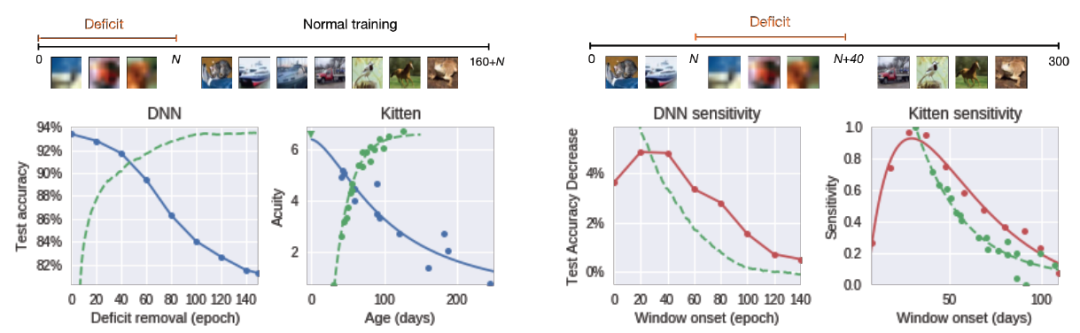
圖 1. DNN 中顯示出的關鍵期
由上述實驗給出的結果人們很自然地會提問:是否輸入數據分布的任何變化都會有一個相應的學習關鍵期?作者表示,對于神經元網絡來說,情況并非如此,它們有足夠的可塑性來適應感覺處理(sensory processing)的 high-level 變化。例如,成年人類能夠迅速適應某些劇烈的變化,如視野的倒置。在圖 2 中,我們觀察到 DNN 也基本上不受 high-level 缺陷的影響—比如圖像的垂直翻轉或輸出標簽的隨機排列。在缺陷修正之后,網絡很快就恢復了它的基線性能。這暗示了數據分布的結構和優化算法之間存在更精細的相互作用,進而導致存在一個關鍵期。
接下來,作者對網絡施加了一個更激烈的缺陷攻擊,令每個圖像都被白噪聲取代。圖 2 顯示,這種極端的缺陷所表現出的效果明顯比只模糊圖像所得到的效果要輕。用白噪聲訓練網絡并不會提供任何關于自然圖像的信息,因此,與其它缺陷(例如,圖像模糊)相比,白噪聲的效果更溫和。不過,白噪聲中包含了一些信息,從而導致網絡(錯誤地)學習圖像中并沒有存在的精細結構。
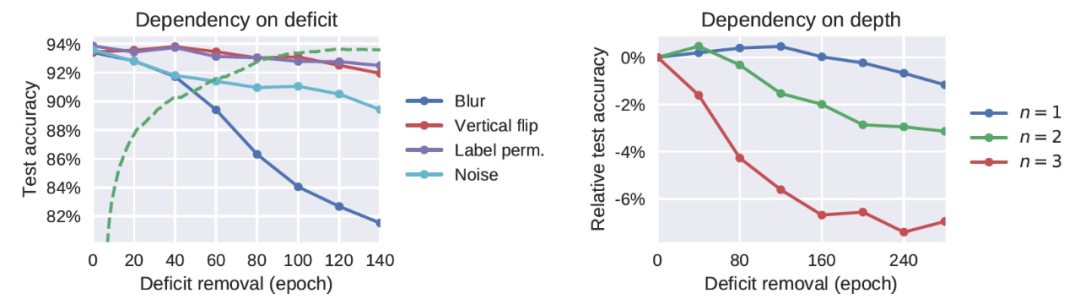
圖 2.(左)High-level 的擾動并不會導致關鍵期。當缺陷只影響 high-level 特征(圖像的垂直翻轉)或 CNN 的最后一層(標簽互換)時,網絡不會表現出關鍵期(測試準確度基本保持平穩)。另一方面,類似于感知剝奪的缺陷(圖像被隨機噪聲取代)確實會導致缺陷,但其影響沒有圖像模糊的情況那么嚴重。(右)關鍵期曲線對網絡深度的依賴情況。添加更多的卷積層會增大關鍵期缺陷的影響。
圖 3 顯示,在 MNIST 庫上訓練的全連接網絡也存在圖像模糊缺陷的關鍵期。因此,作者認為(對于重現模型訓練的關鍵期)卷積結構不是必需的,使用自然圖像也不是必需的。同樣,在 CIFAR-10 上訓練的 ResNet-18 也有一個關鍵期,它也比標準卷積網絡中的關鍵期明顯更清晰(圖 1)。作者分析,ResNets 允許梯度更容易地反向傳播到低層,其關鍵期的存在可以表明關鍵期不是由梯度消失引起的。圖 2(右)顯示,關鍵期的存在確實關鍵地取決于網絡的深度。在圖 3 中,作者確認,即使在網絡以恒定的學習速率訓練時,也存在一個關鍵期。圖 3(右下角)顯示,當使用 Adam 作為優化器時,使用其前兩個時刻的運行平均值對梯度進行重歸一化,我們仍然觀察到一個與標準 SGD 類似的關鍵期。改變優化的超參數可以改變關鍵期的形狀:圖 3(左下角)顯示,增加權重衰減(weight decay)使關鍵期更長,更不尖銳。這可以解釋為它既減慢了網絡的收斂速度,又限制了 high-level 為克服缺陷而改變的能力,從而鼓勵 low-level 也學習新特征。
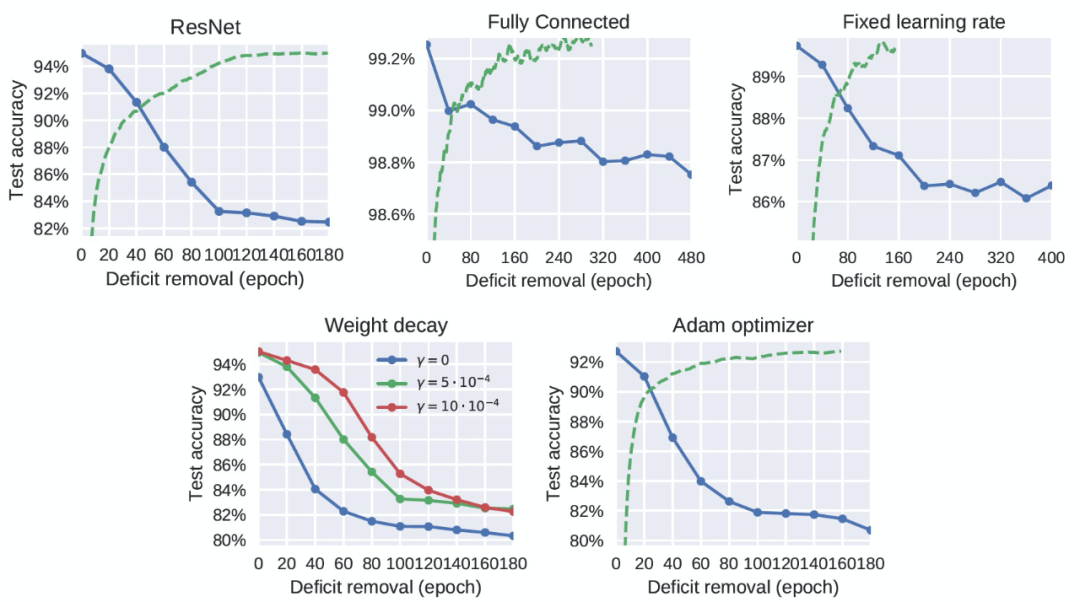
圖 3. 不同 DNN 架構和優化方案中的關鍵期
1.2 Fisher 信息分析
作者根據經驗確定,在動物和 DNN 中,訓練的早期階段對訓練過程的結果至關重要。在動物中,這與缺陷有關的區域的大腦結構變化密切相關。這在人工網絡中不可避免地有所不同,因為它們的連接性在訓練期間一直都是固定的。然而,并不是所有的連接對網絡都同樣有用。考慮一個編碼近似后驗分布 p_ω(y|x)的網絡,其中,ω表示權重參數。來自特定連接的最終輸出的依賴性可以通過擾動相應的權重和觀察最終分布的變化幅度來估計。給定權重擾動ω'=ω+δω,p_ω(y|x)和由擾動生成的 p_ω'(y|x)之間的偏差可以由 K-L 散度度量,即:
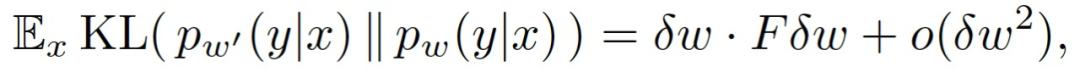
其中的 F 為 Fisher 信息矩陣(Fisher Information Matrix,FIM):
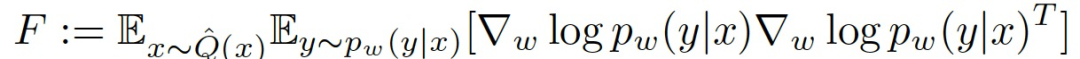
FIM 可以被認為是一個局部指標,用于衡量一個單一權重(或一個權重組合)的擾動對網絡輸出的影響程度。特別是,具有低 Fisher 信息的權重可以被改變或 "修剪",對網絡的性能影響不大。這表明,Fisher 信息可以作為 DNN 有效連接的衡量指標,或者,更廣泛地說,作為連接的 "突觸強度(synaptic strength)" 的衡量標準。最后,FIM 也是損失函數 Hessian 的半定逼近,因此也是訓練過程中某一點ω的損失情況的曲率,在 FIM 和優化程序之間提供了一種關聯性。
不幸的是,完整的 FIM 太大,無法計算。因此,本文作者使用它的軌跡來測量全局或逐層的連接強度。作者提出使用以下方法計算 FIM:
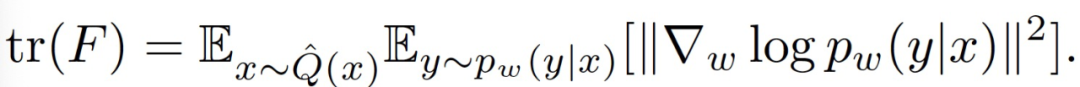
為了捕捉非對角線項的行為,作者還嘗試使用 Kronecker-Factorized 近似計算全矩陣的對數行列式。作者觀察到了與 trace 相同的定性趨勢。由于 FIM 是一個局部測量,它對損失情況的不規則性非常敏感。因此,作者在文中主要使用 ResNets,ResNets 具備相對平滑的損失情況。對于其他架構,作者則使用一個基于在權重中注入噪聲的更穩健的 FIM 估計器。
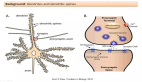
FIM 可以被確定為對模型中包含的訓練數據信息量的一種衡量。在此基礎上,人們會期望隨著從經驗中獲得信息,連接(connection)的總體強度會單調地增加。然而,情況并非如此。雖然在早期階段網絡就獲得了有關數據的信息,從而使得連接強度的大幅增加,但一旦任務的表現開始趨于平穩,網絡就開始降低其連接的整體強度。然而,這并不對應于性能的降低,相反,性能一直在緩慢提高。這可以被看作是一個 "遺忘" 或 "壓縮" 階段,在這個階段,多余的連接被消除,數據中不相關的變化被拋棄。在學習和大腦發育過程中,消除("修剪")不必要的突觸是一個基本的過程,這一點已經得到了前期研究的證實(圖 4,中心)[8]。在圖 4(左)中,類似的現象在 DNN 中得到了清晰和定量的顯示。
連接強度的這些變化與對關鍵期誘發的缺陷(如圖像模糊)的敏感性密切相關,如圖 1 中使用 "滑動窗口" 方法計算。在圖 4 中,我們看到敏感性與 FIM 的趨勢密切相關。FIM 是在沒有缺陷的情況下在網絡訓練過程中的一個點上計算的局部數量,而關鍵期的敏感性是在有缺陷的網絡訓練結束后,使用測試數據計算的。圖 4(右)進一步強調了缺陷對 FIM 的影響:在存在缺陷的情況下,FIM 會增長,甚至在缺陷消除后仍然大幅增長。作者分析,這可能是由于當數據被破壞到無法分類時,網絡被迫記憶標簽,因此增加了執行相同任務所需的信息量。
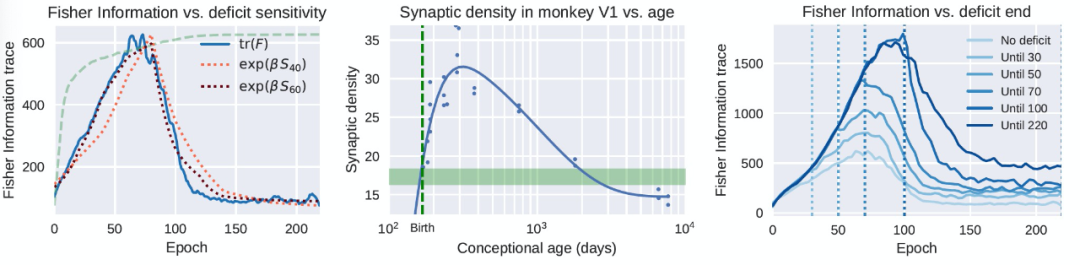
圖 4. DNN 的關鍵期可追溯到 Fisher 信息的變化
對 FIM 的逐層分析進一步揭示了缺陷對網絡的影響。在沒有缺陷的情況下訓練網絡時(在這種情況下是 All-CNN,它比 ResNet 有更清晰的層次劃分),最重要的連接是在中間層(圖 5,左),它可以在最有信息量的中間尺度上處理輸入的 CIFAR-10 圖像。然而,如果網絡最初是在模糊的數據上訓練的(圖 5,右上方),連接的強度是由頂層(第 6 層)主導的。作者分析,這是因為圖像的低層和中層結構被破壞了。然而,如果在訓練的早期消除缺陷(圖 5,頂部中心),網絡會設法 "重組",以減少最后一層所包含的信息,同時增加中間層的信息。作者把這些現象稱為 "信息可塑性" 的變化。然而,如果數據變化發生在鞏固階段(consolidation phase)之后,網絡就無法改變其有效連接。每層的連接強度基本上保持不變。此時,網絡失去了它的信息可塑性,錯過了它的關鍵期。
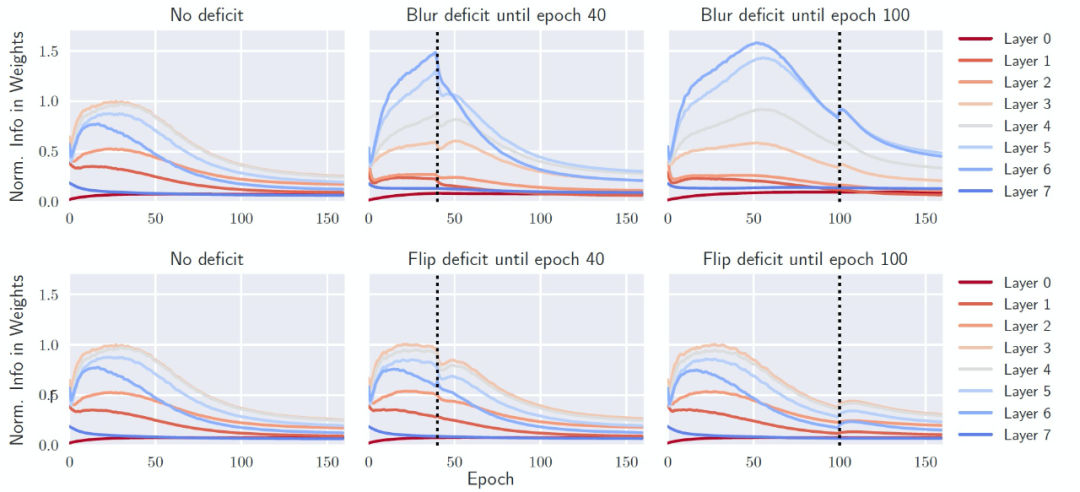
圖 5. 各層權重所含信息的歸一化數量與訓練 epoch 的關系。(左上)在沒有缺陷的情況下,網絡主要依靠中間層(3-4-5)來解決任務。(右上)在存在圖像模糊缺陷的情況下,直到第 100 個 epoch,更多的資源被分配到高層(6-7),而不是中間層。(頂部中心)當缺陷在較早的 epoch 被消除時,各層可以部分地重新配置 (例如,第 6 層中信息的快速損失)。(最下面一行) 同樣的圖,但引入的是翻轉缺陷,并不會誘發關鍵期
最后,對 FIM 的分析也揭示了損失函數的幾何形狀和學習動態。由于 FIM 可以被解釋為殘余分布 (landscape) 的局部曲率,圖 4 顯示,學習需要越過瓶頸階段。在初始階段,網絡進入高曲率的區域(高 Fisher 信息),一旦開始進入鞏固階段,曲率就會下降,使其能夠跨越瓶頸以進入后續階段。收斂的早期階段是引導網絡走向 "正確的" 收斂結果的關鍵。關鍵期的結束是在網絡跨越了所有的瓶頸(從而學會了特征)并進入一個收斂區域(低曲率的權重空間區域,或低 Fisher 信息)之后。
1.3 討論
到目前為止,關鍵期仍被認為是一種專門的生物現象。同時,對 DNN 的分析主要集中在其漸進特性上,而忽略了其初始的瞬態行為。作者表示,本文是第一個探討人工神經網絡臨界期現象的文章,并強調瞬態在決定人工神經網絡的漸進性能中的關鍵作用。受突觸連接在調節關鍵期作用的啟發,作者引入了 Fisher 信息來研究這個階段。文章表明,對缺陷的最初敏感性與 FIM 的變化密切相關,既是全局性的,因為網絡首先迅速增加,然后減少儲存的信息量;也是分層的,因為網絡 "重組" 其有效連接,以最佳方式處理信息。
本文工作與生物學中關于關鍵期的大量文獻相關。盡管人工網絡是神經元網絡的一種極其簡化的近似,但它們表現出的行為與在人類和動物模型中觀察到的關鍵期有本質上的相似。本文給出的信息分析表明,DNN 中最初的快速記憶階段之后是信息可塑性的損失,這反過來又進一步提高了其性能。在文獻 [9] 中,作者觀察到并討論了訓練的兩個不同階段的存在,他們的分析建立在激活的(香農)信息上,而不是權重的(費雪)Fisher 信息。在多層感知器(MLP)上,文獻 [9] 根據經驗將這兩個階段與梯度協方差的突然增加聯系起來。然而,必須注意的是,FIM 的計算是使用與模型預測有關的梯度,而不是與 ground-truth 標簽有關的梯度,這就會導致質量差異。圖 6 顯示梯度的均值和標準偏差在有缺陷和無缺陷的訓練中沒有表現出明顯的趨勢,因此,與 FIM 不同,它與對關鍵期的敏感性沒有關聯。
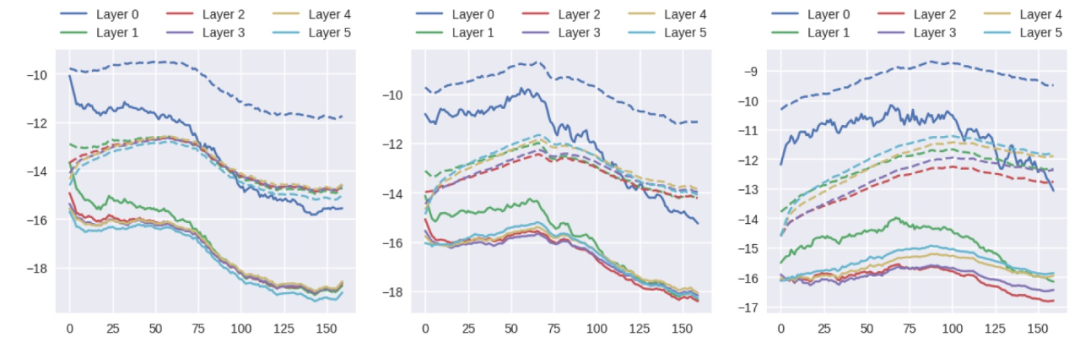
圖 6. 訓練期間梯度均值(實線)和標準偏差(虛線)的對數值。(左)不存在缺陷,(中)第 70 個 epoch 后出現模糊缺陷,(右)最后一個 epoch 出現缺陷。
除了與關鍵期的缺陷敏感性有密切的關系外,Fisher 信息還具有一些技術優勢,包括對角線易估計、對互信息的選擇估計器不敏感,以及能夠輔助探測人工神經網絡中各層有效連接的變化情況。
對激活的完整分析不僅要考慮到信息量(包括與任務有關的和與干擾有關的),還要考慮其可及性,例如,與任務有關的信息能多容易被一個線性分類器提取出來。按照類似的想法,Montavon 等人 [10] 通過對每層表征的徑向基函數(RBF)核嵌入進行主成分分析(PCA),研究了表征的簡單性的逐層或 "空間"(不是時間)的演變。他們表明,在多層感知器上,與任務相關的信息更多地集中在表征嵌入的第一個主成分上,從而使得它們變得更容易被逐層 "訪問"。本文工作專注于權重的時間演變。一個具有較簡單權重的網絡(由 FIM 測量)也需要一個較簡單的平滑表示(如由 RBF 嵌入測量),以抵抗權重的擾動從而正常運行。因此,本文分析與 Montavon 等人的工作是一致的。同時使用這兩個框架來研究網絡的聯合時空演變情況將會非常有趣。
關注權重信息而不是激活或網絡行為的一個好處是:在關鍵期有一個 "有效連接" 的讀數。在人工和神經元網絡中,消除缺陷后的 "行為" 讀數有可能被視覺通路不同層次的缺陷適應性變化所混淆。
Knudsen 對動物模型中的關鍵期給出了一個精辟的解釋:神經元網絡的初始連接是不穩定的,容易修改(高度可塑性),但隨著觀察到更多的 "樣本",它們會發生變化并達到一個更穩定的配置,難以修改[11]。然而,在新創建的連接模式中仍然可以存在學習。這與本文的研究結果基本一致。當連接被重塑時,對關鍵期誘導缺陷的敏感度達到峰值(圖 4,左),并且在有缺陷和無缺陷的網絡中觀察到不同的連接圖譜(圖 5)。對于高級別的缺陷來說,如圖像翻轉和標簽置換,不需要對網絡的連接進行徹底的重組就能糾正缺陷,因此不存在關鍵期。
此外,本文的工作也可以與預訓練進行比較。Erhan 等人研究了某種相關的、但現在很少使用的層間無監督預訓練的做法,并認為可以將它用作一個正則化算子(regularizer)從而將網絡的權重向更接近好的解決方案的損失情況移動,而且早期樣本在引導網絡向特定解決方案移動方面具有更好的效果[12]。
圖 4 表明,SGD 在網絡訓練中經歷了兩個不同的階段。起初,網絡向損失情況的高曲率區域移動;而在第二階段,曲率下降,網絡最終收斂到一個平坦的最小值。作者把這些解釋為網絡在訓練過程中為了學習有用的特征而跨越了瓶頸,最終在學習完成后進入損失面的平坦區域。當把這一假設與缺陷敏感性分析結合起來時,我們可以假設,關鍵期恰恰發生在跨越這一瓶頸時。同樣值得注意的是,有證據表明,在 DNN 中收斂到平坦的最小值(低曲率的最小值)與良好的泛化性能相關。與該解釋一致,圖 4(右)顯示,受缺陷影響較大的網絡最終會收斂到更尖銳的最小值。然而,我們也發現,網絡的性能在早期的 "敏感" 階段已經基本確定。因此,作者也承認,實驗中收斂時的最終銳度可能是一個偶發現象,而不是已經經過良好總結和概括后推導出的原因。
本文的研究目標并不是通過人工網絡來研究人類(或動物)的大腦,而是了解基本的信息處理現象,包括其在生物和人工的實現。此外,作者強調盡管文中的分析和實驗顯示生物大腦或人工網絡都存在關鍵期,但并不是說 DNN 就一定是神經生物學信息處理的有效模型。關于 "人工神經科學" 的工作,其研究部分是為了滿足開發 "可解釋的" 人工智能系統的技術需要,以使得這些系統的行為可以被理解和預測。神經科學家往往采用數學模型來研究生物現象,而我們選擇利用周知的生物現象來幫助理解人工網絡的信息處理。反過來說,探討如何測試生物網絡修剪連接是否是信息可塑性損失的結果,而不是原因,也將是很有趣的。學習和發展過程中網絡重構的機制可能是在基本信息處理現象的推動下獲得的進化結果。
2 深度神經網絡優化軌跡的損益平衡點 [5]

這篇文章與嚴格意義上生物學概念的 “關鍵期” 并無直接關聯,它聚焦的問題是“深度神經網絡的早期訓練階段對其最終性能影響的重要性”。盡管它并沒有與生物學理念相關聯,但其探討的是深度學習中關鍵學習期(早期訓練階段)問題,所以我們也對本文進行解讀。
2.1 問題闡述
近年來,關于深度神經網絡(DNNs)的研究和應用發展迅速,但關于其優化和泛化能力之間的聯系并沒有被完全理解。例如,使用一個大的初始學習率往往能夠提高 DNNs 的泛化能力,但卻是以減少初始訓練損失為代價的。相比之下,使用批歸一化層(batch normalization layers)通常可以提高深度神經網絡的泛化能力和收斂速度。關于深度神經網絡早期訓練階段的研究是解決 DNN 優化和泛化能力之間聯系的有效途徑。例如,在訓練的早期階段引入正則化處理是實現良好泛化能力的必要條件。
本文具體研究了優化軌跡對訓練的早期階段的依賴性。作者引入梯度協方差研究小批量梯度的噪聲,引入 Hessian 研究損失面的局部曲率,梯度協方差矩陣和 Hessian 矩陣能夠有效捕捉 DNN 的優化和泛化性能的重要性和互補能力。此外,作者陳述并提出了關于優化軌跡對訓練早期階段的依賴性的兩個猜想的經驗證據。最后,作者將本文分析應用于具有批歸一化(batch normalization,BN)層的網絡,發現本文的預測在這種情況下也是有效的。
2.2 損益平衡點和關于 SGD 軌跡的兩個猜想
作者的研究動機是為了更好地理解 DNNs 的優化和泛化能力之間的聯系。在本節中,作者具體研究梯度的協方差(K)和 Hessian(H)如何取決于訓練的早期階段。
首先,定義樣本 (x,y) 的損失為 L(x,y; θ),其中θ為 D 維參數向量。訓練損失的 Hessian 矩陣記為 H,梯度協方差矩陣記為:
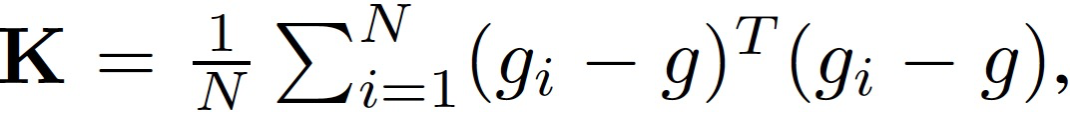
其中,g_i 表示梯度,g 為全批次梯度。
作者引入以下條件來量化給定θ(t)的穩定性。參數θ投射到(e_H)^1 表示為下式((e_H)^1 為 H 的第 1 個特征向量):
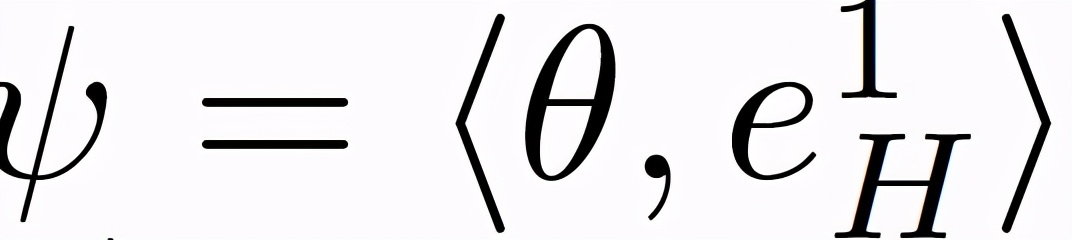
可以令
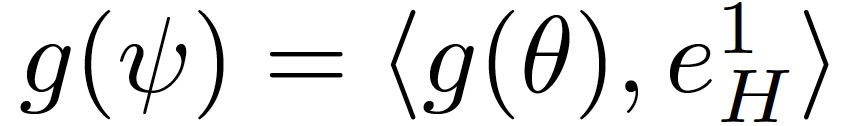
如果下列序列的范數在τ趨向于無窮大時不收斂,則稱 SGD 沿(e_H)^1 是不穩定的:
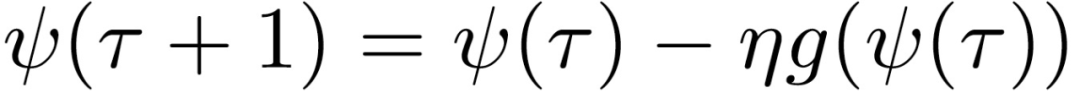
其中,ψ(0)=θ(t)。序列ψ(t)表征每一步驟 t’>t 映射到(e_H)^1 中的優化策略。
假設。根據實證研究的結論,作者做了以下假設:
1. 投影到(e_H)^1 的損失面是一個二次一維函數。
2. 特征向量(e_H)^1 和(e_K)^1 是共線的。
3. 如果沿(e_H)^1 優化在下一步會出現下降,則沿(e_H)^1 方向距離最小值的距離值在下一步會增大。
4. H 的譜范數(λ_H)^1 在訓練階段增大,沿(e_H)^1 方向距離最小值的距離值減小,如果不滿足,則增大(λ_H)^1 會導致進入一個特定區域,該區域中沿(e_H)^1 方向的訓練是不穩定的。
此外,作者還假設 S≥N,即,與訓練樣本的數量相比,批處理的規模較小。
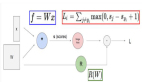
較大的學習率或較小的批處理量會更早達到損益平衡點。僅考慮從θ(0)開始的訓練,且沿 (e_H)^1(0)^2 的 SGD 穩定。本文目標是證明學習率(η) 和批大小 (S) 在本文模型中決定了 H 和 K,并猜想其它神經網絡在經驗上也是如此。
給定η_1 和 η_2 對應的優化軌跡,η_1 > η_2,二者從相同的θ_0 初始化。根據假設 1,沿 (e_H)^1(t) 的損失面為:
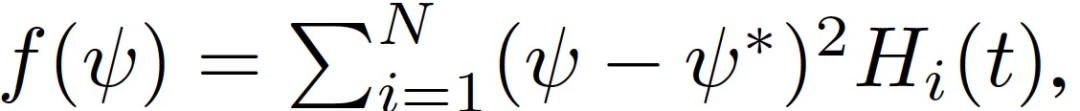
可以證明,在任何迭代 t,SGD 沿 (e_H)^1(t) 穩定的必要和充分條件是
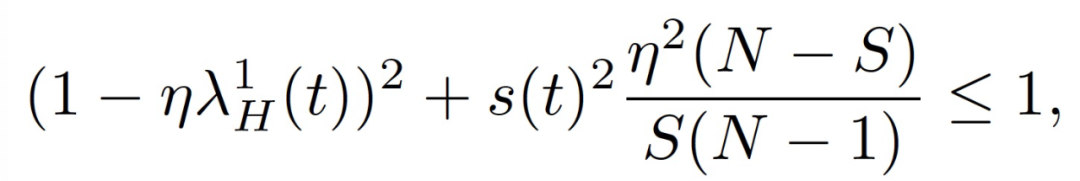
N 為訓練樣本集大小,s(t)^2=Var[H_i(t)]。作者把上式中公式左邊第一次變為 1 時對應的軌跡上的這一點稱為損益平衡點(break-even point)。根據定義,訓練軌跡上只存在一個損益平衡點。
根據假設 3 可知,(λ_H)^1(t)和 (λ_K)^1(t) 隨時間增大。當 S=N,損益平衡點為(λ_H)^1(t)=2/η。由假設 4 可知,在通過訓練軌跡上的損益平衡點后,SGD 不會進入(λ_H)^1 或(λ_K)^1 大于損益平衡點的區域,否則會導致上式左半部分中的一個項增加,從而沿(e_H)^1 失去穩定性。
關于 DNN 的兩個猜想。假設 DNN 達到了損益平衡點,作者對其優化軌跡提出以下兩個猜想。達到損益平衡點的最直接含義是,損益平衡點的(λ_H)^1 和(λ_K)^1 取決于η和 S,將其形式化為:
猜想 1(SGD 的方差減少效應)。沿著 SGD 的軌跡,在較大的學習率或較小的批處理規模下,(λ_H)^1 和(λ_K)^1 的最大值較小。
猜想 2(SGD 的預處理效果)。沿著 SGD 的軌跡,學習率越大或批越小,則有 ((λ_H)^*)/((λ_H)^1) 和((λ_K)^*)/((λ_K)^1)的最大值就越大,其中λ_K * 和λ_H * 分別是 K 和 H 的最小非零特征值。此外,對于較大的學習率或較小的批規模,Tr(K)和 Tr(H)的最大值也較小。
作者在猜想中考慮了非零特征值,因為 K 最多有 N-1 個非零特征值,其中 N 是訓練數據的數量,這一數量在超參數化的 DNN 中可能比 D 小很多。這兩個猜想只對能夠保證訓練收斂的學習率和批大小有效。
2.3 實驗分析
作者首先分析了訓練早期階段的學習情況。接下來,對兩個猜想進行了經驗性研究。在最后一部分,作者將分析擴展到具有批規一化層的神經網絡。作者在實驗中使用的數據庫包括 CIFAR-10、IMDB、ImageNet、MNLI。使用的網絡結構包括 SimpleCNN、ResNet-32、LSTM、DenseNet、BERT。
本文理論模型的關鍵假設是,(λ_H)^1 和(λ_K)^1 是相關的,至少在達到損益平衡點之前是這樣的。作者在圖 7 中證實了這一點。對于較小的η來說,(λ_H)^1 和(λ_K)^1 可得的最大值是較大的。根據假設 3,(λ_H)^1 和(λ_K)^1 的增大會導致穩定性的降低,作者將其形式化為沿(e_H)^1 的穩定性。不過,直接計算沿(λ_H)^1 的穩定性的計算代價非常高。因此,作者轉為測量一個更實用的度量標準:在每一次迭代中,連續兩個步驟之間的訓練損失的差異ΔL。
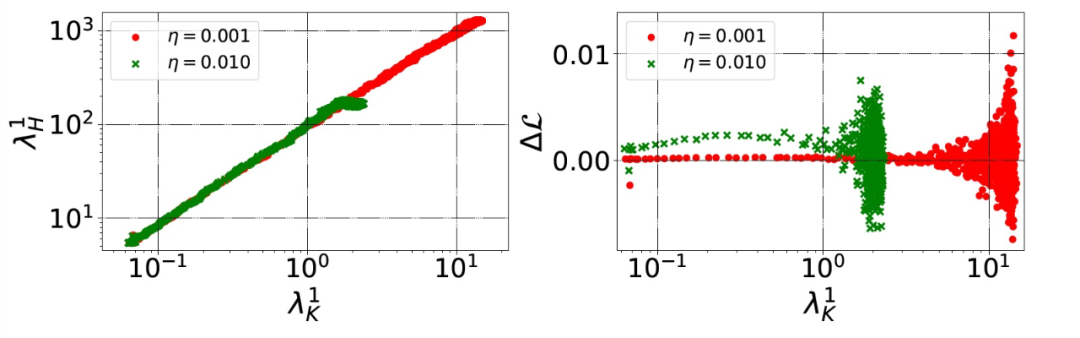
圖 7. 在不同的訓練迭代中,H 的譜范數(左)和ΔL(在兩個連續步驟之間計算的訓練損失的差異,右)與(λ_K)^1 的對比。用 SimpleCNN 在 CIFAR-10 數據庫上進行實驗,有兩種不同的學習率(顏色不同)
接著,作者對猜想 1 和猜想 2 進行了經驗性驗證。對于每個模型,手動選擇合適的學習率和批大小,以確保 K 和 H 的屬性在合理的計算代價下收斂。實驗中主要是研究梯度的協方差(K),當改變訓練的批大小時,使用 128 的批大小來計算 K。當改變學習率時,使用與訓練模型相同的批大小。圖 8 中給出實驗結果。
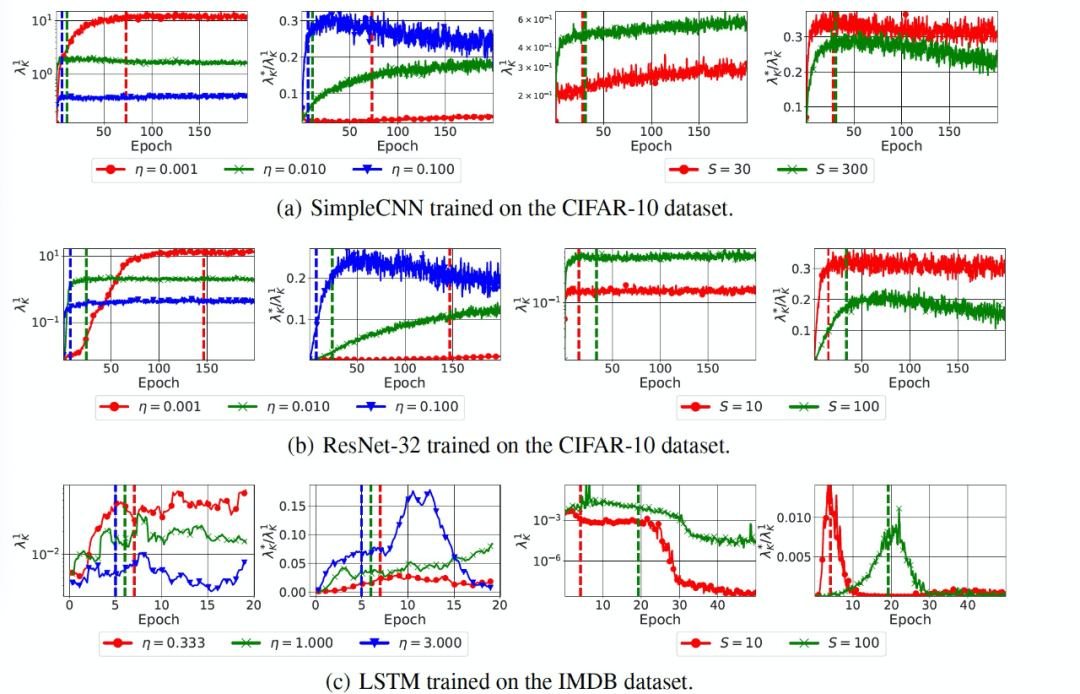
圖 8. SGD 的方差減少和預處理效果。與較大的學習率(η)或較小的批大小(S)相對應的優化軌跡的特點是較低的最大(λ_K)^1(梯度協方差的譜范數)和較大的最大((λ_K)^*)/((λ_K)^1)(梯度協方差的條件數)。垂直線標志著訓練準確度大于(第一次)手動挑選的閾值的 epoch,這說明這些影響不是由訓練速度的差異所解釋的。
然后,作者在兩個更大規模的環境中測試這兩個猜想:BERT 在 MNLI 數據庫上進行微調,DenseNet 在 ImageNet 數據庫上進行訓練。由于內存的限制,作者在實驗中只改變了學習率。圖 9 給出了實驗結果。我們觀察到,這兩個猜想在這兩種情況下都成立。值得注意的是,DenseNet 使用了批歸一化層。
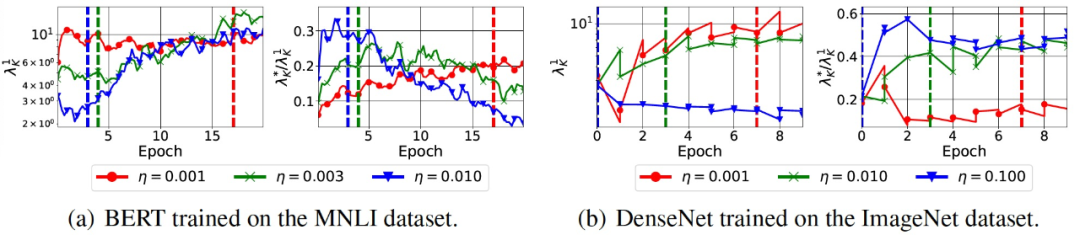
圖 9. Variance 減少和 SGD 的預調效果
最后的實驗是關于在具有批規一化層的網絡中,學習率對調節(conditioning)的重要性。深度神經網絡的損失面是 ill-condition 的。近年來,一些研究人員認為批規一化具有有效性的關鍵原因是能夠改善損失面的 conditioning。為了研究猜想是否在具有批歸一化層的網絡中成立,作者在 CIFAR-10 數據庫上使用具有批歸一化層的 SimpleCNN 模型(SimpleCNN-BN)進行了實驗。結果見圖 10。
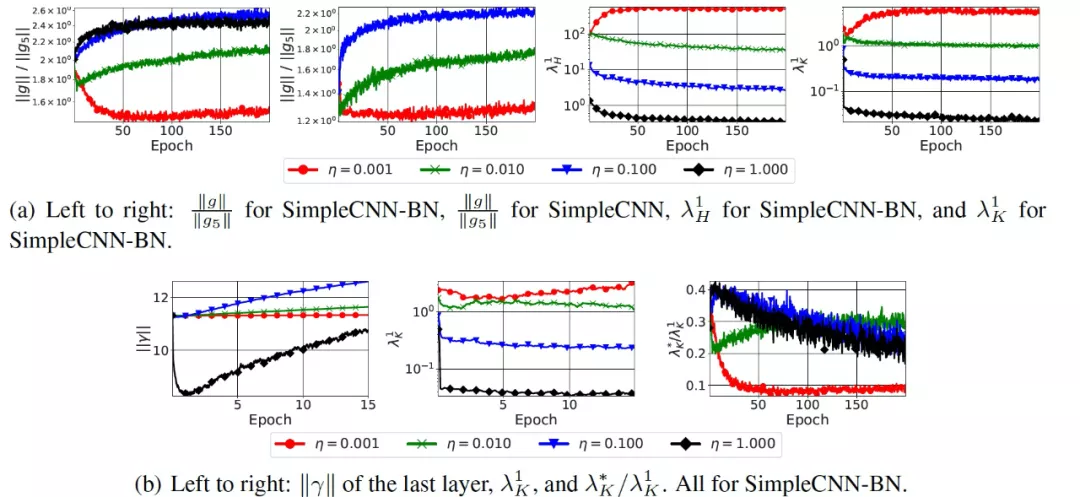
圖 10. 改變學習率對各種指標的影響,SimpleCNN 有和沒有批規一化層(SimpleCNN-BN 和 SimpleCNN)
由圖 10(底部)可知,SimpleCNN-BN 的訓練開始于一個 (λ_K)^1 相對較高的區域。這與之前研究的結論是一致的[13],即帶有批歸一化層的網絡在第一次迭代中會出現梯度爆炸的現象。然后,除了最低的η值之外,所有的(λ_K)^1 值都會衰減。這種行為與本文的理論模型是一致的。作者還跟蹤了圖 10(底部)中網絡最后一層的批歸一化層中的縮放因子的范數 ||γ||。作者比較了兩種設置。SimpleCNN-BN,η=0.001;SimpleCNN,η=0.01。作者得出了三個觀察結果。首先,||g||/||g_5|| 的最大值和最小值分別為 1.90(1.37) 和 2.02(1.09)。第二,(λ_K)^1 的最大值和最小值分別為 12.05 和 3.30。最后,((λ_K)^*)/((λ_K)^1)在第一個設定中達到 0.343,在第二個設定中達到 0.24。將這些差異與 SimpleCNN-BN 中使用最高η=1.0 所引起的差異相比較,作者得出結論:使用較大的學習率會導致損失平滑的效果,而這在以前只會由批規一化處理所導致。
作者證明,猜想 1 和猜想 2 中預測的學習率的影響在有批歸一化層的網絡中是成立的,與沒有批歸一化層的同一網絡中損失面的調節(conditioning)相比,在有批歸一化層的網絡中使用較大的學習率對于改進損失面的調節是有效的。
3 神經網絡早期學習動力學的簡單性 [4]

現代神經網絡通常被認為是復雜的黑箱函數,由于其對數據的非線性依賴和損失情況(loss landscape)的非凸性,其工作過程和輸出結果難以理解。在本文的工作中,作者嘗試分析和證明神經網絡的早期學習階段的情況可能并非如此。作者在文章中證明,對于一類 well-behaved 輸入分布,在早期訓練階段,具有任何共同激活的兩層全連接神經網絡的梯度下降動態變化過程都可以通過訓練一個針對此輸入的簡單模型來模仿。當只訓練第一層時,這個簡單的模型是輸入特征的線性函數;當訓練第二層或兩層時,它是特征和其 L_2 范數的線性函數。這一結果意味著,神經網絡直到訓練的后期階段才會完全發揮其非線性能力。
3.1 兩層神經網絡
考慮一個有 m 個隱藏神經元的兩層全連接神經網絡,定義為:
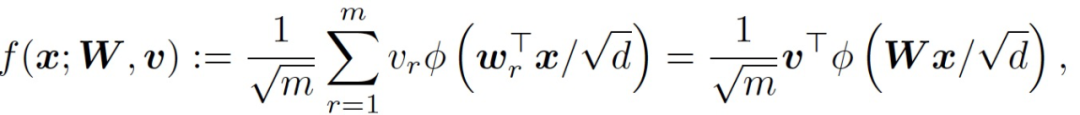
(1)
其中,x 為輸入,W 為第一層的權重矩陣,v 為第二層的權重向量,φ為激活函數。令 {(x_i,y_i)} 表征 n 個訓練樣本,x_i 為輸入,y_i 為對應的輸出。X 為數據矩陣,y 為對應的標簽向量。考慮 L_2 訓練損失如下:
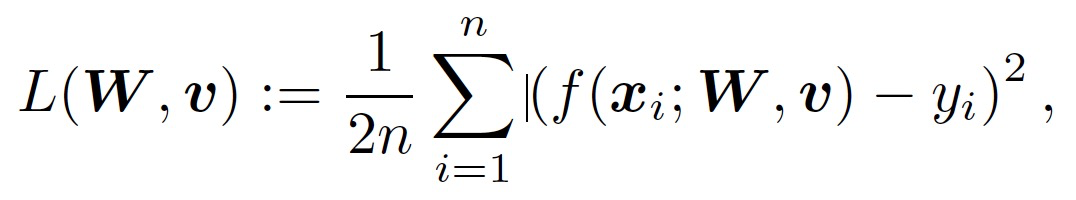
(2)
從隨機初始化開始對目標公式(2)運行梯度下降(Gradient descent, GD)處理。具體來說,對權重(W, v)進行以下對稱初始化處理:
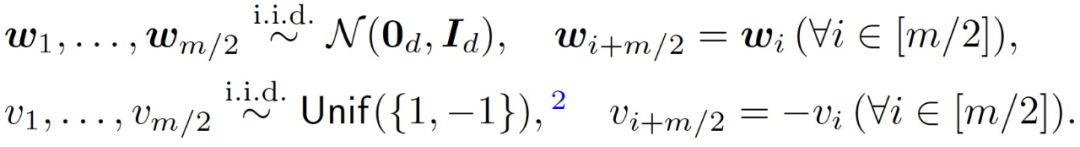
(3)
令 (W(0), v(0)) 表征一組從對稱初始化公式 (3) 中提取的初始權重。然后根據 GD 來更新權重:
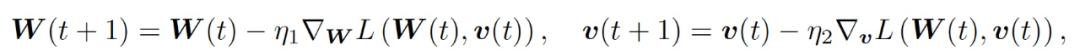
(4)
其中,η_1 和η_2 分別為學習速率。
接下來,作者給出輸入分布假設。
假設 3.1(輸入分布)。數據 x_1,...,x_n 是來自均值為 0、協方差為 0 的分布 D 的獨立同分布(i.i.d.)樣本,使得 Tr[∑]=d 和 ||∑||=O(1)。此外,x~ D 可以寫成 x =∑^(1/2) 1x,其中 x 的輸入是獨立的,都是 O(1)-subgaussian 的。
假設 3.2(激活函數)。激活函數φ滿足以下任一條件:(i)平滑激活:φ具有有界的一階和二階導數:
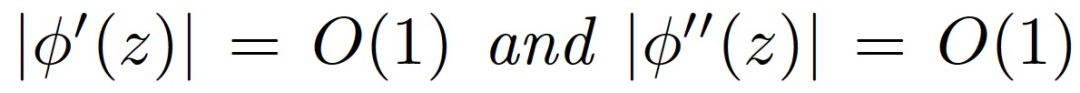
或 (ii) 塊狀線性激活:
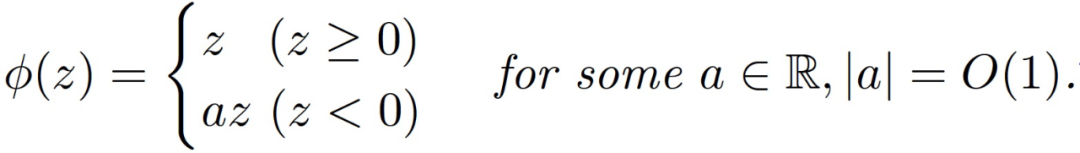
Claim3.1。假設 n 遠大于 d,那么在假設 3.1 下,我們有很大概率能夠得到:
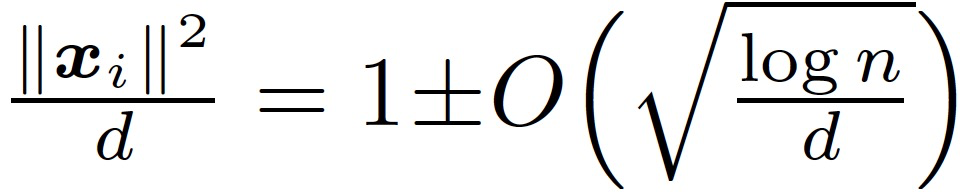
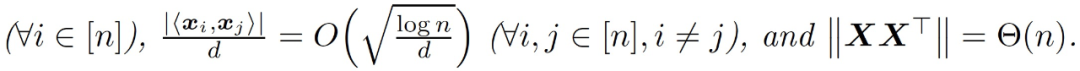
本節的結果是證明由 GD 訓練的神經網絡在訓練的早期階段近似于一個線性函數。由于神經網絡中兩層的貢獻是不同的,作者將后續討論分為只訓練第一層、只訓練第二層和兩層一起訓練。
3.1.1 只訓練第一層
只考慮訓練第一層權重 W,這相當于在公式(4)中設置η_2=0。在訓練的早期階段,引入一個用于模仿神經網絡(f_t)^1 的線性模型:
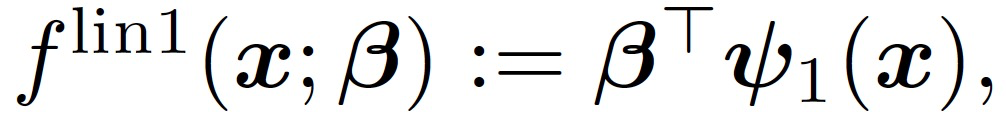
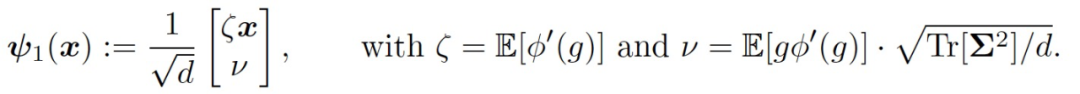
(5)
考慮通過 GD 在 L_2 損失上從零開始訓練這個線性模型:
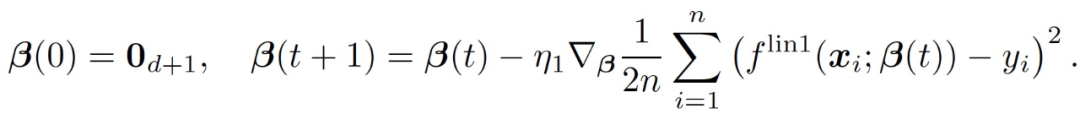
(6)
定理 3.2(訓練第一層的主要定理)。令α∈(0,1/4)為一個固定的常數。假設訓練樣本的數量 n 和網絡寬度 m 滿足
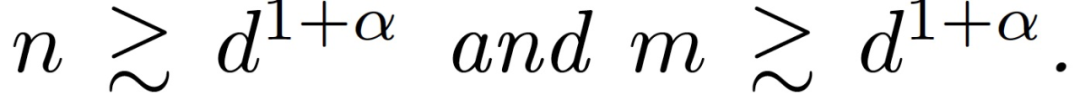
假設η_1 遠小于 d,η_2 = 0,那么存在一個常數 c > 0,在很大的概率下對于所有 t 神經網絡和線性模型在訓練數據上平均接近。
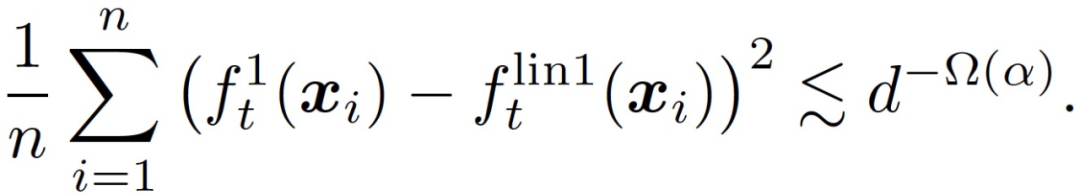
(7)
大概率地,對于所有的 t,我們有
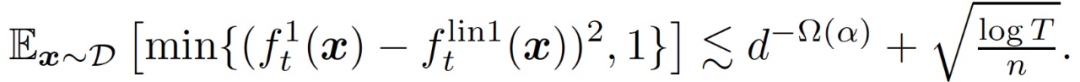
(8)
3.1.2 只訓練第二層
只考慮訓練第二層權重 v,這相當于在公式(4)中設置η_1=0。在訓練的早期階段,用于模仿神經網絡(f_t)^2 的線性模型是
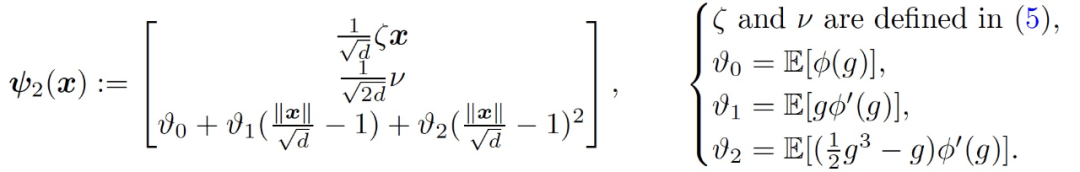
(9)
從零開始,使用 GD 訓練該線性模型:
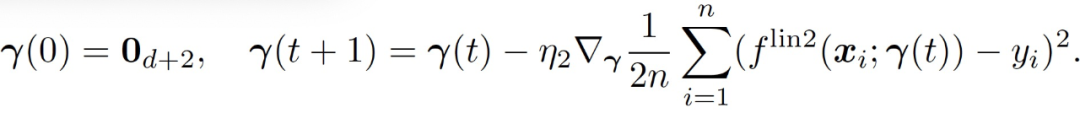
(10)
令(f_t)^lin2 表征第 t 輪循環的結果模型。
嚴格意義上講 f^lin2(x;γ)并不是關于 x 的線性模型,不過在本文分析的數據中,根據 Claim3.1,||x||/sqrt(d)≈1,所以非線性的特征幾乎可以忽略。與第一層的訓練類似,本文用于訓練第二層的主要定理如下:
定理 3.5(訓練第二層的主要定理)。令α為常數,假設:
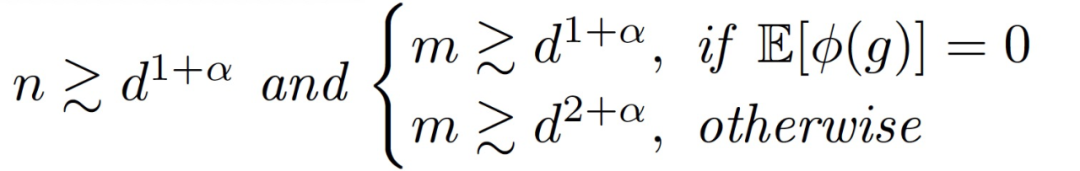
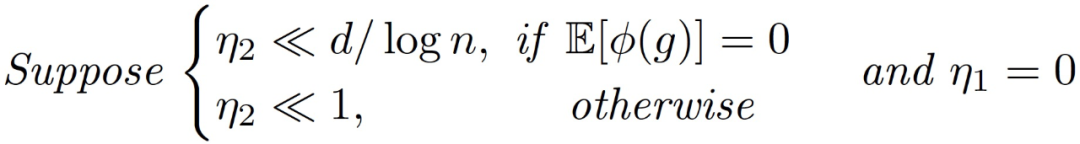
存在一個常數 c>0,在很高的概率下,對所有 t 同時我們有
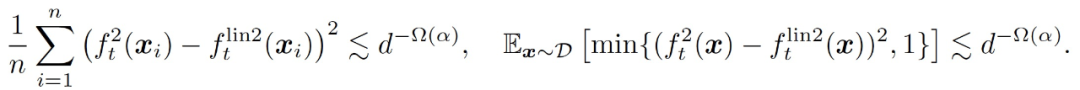
3.1.3 同時訓練兩層
最后,考慮同時訓練兩層的情況,這相當于在公式(4)中設置η_1=η_2=η>0。在訓練的早期階段,用于模仿神經網絡(f_t)^2 的線性模型是
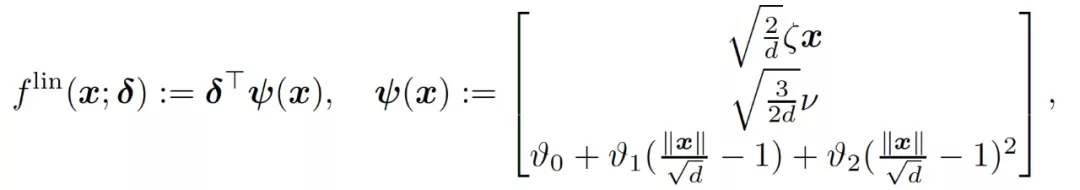
(11)
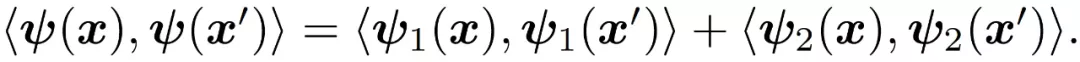
3.2 初步驗證
作者通過在 x~ N(0, I)和 y = sign(f*(x))產生的合成數據上訓練一個具有誤差函數(erf) 激活和寬度為 256 的兩層神經網絡來驗證上文的理論,其中 f* 是一個寬度為 5 的真實兩層誤差函數(erf) 網絡。在圖 11a 中,作者給出了神經網絡的訓練和測試損失(藍色)和其相應的線性模型 f^lin(紅色)。在早期訓練階段(最多 1,000 step),網絡和線性模型的訓練 / 測試損失是很難區分的。之后,達到最佳的線性模型后網絡會持續改進。在圖 11b 中,作者給出了網絡和線性模型在 5 個隨機測試例子上的輸出(logits)的演變過程,我們可以看到,每個單獨的樣本在訓練的早期階段也展現出了很好的一致性。最后,在圖 11c 中,作者改變了輸入維度 d,并為每種情況繪制了網絡輸出和線性模型之間差異的均方誤差(MSE)。我們看到,差異確實隨著 d 的增大而變小,與前文的理論預測相吻合。
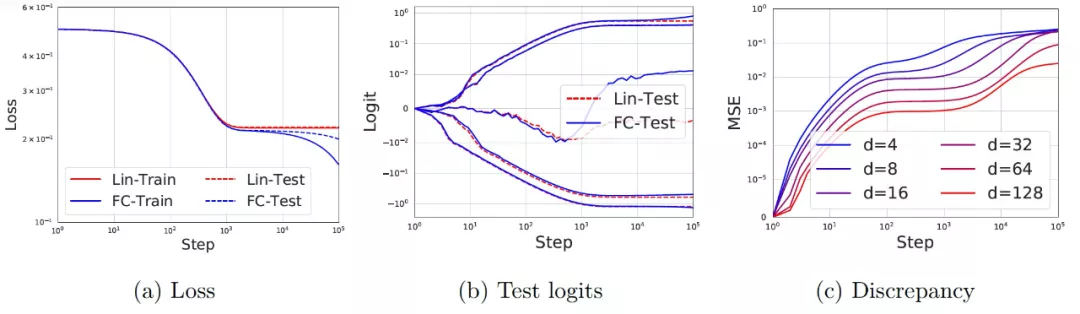
圖 11. 兩層神經網絡在訓練初期學習了一個線性模型。(a) 神經網絡的損失和由公式 (11) 預測的相應線性模型。實線(虛線)代表訓練(測試)損失。d = 50,并使用 20,000 個訓練樣本和 2,000 個測試樣本。神經網絡和線性模型在最初的 1000step 中是很難區分的,之后線性學習結束,網絡繼續改進。(b) 5 個隨機測試例子的 logits(即輸出)演變。我們看到神經網絡的預測和線性模型在早期的預測階段具有很好的一致性。(c)在不同的 d 值下,網絡的輸出和線性模型之間的差異(MSE)。
然后,作者通過一個學習范數相關函數的實驗來說明在公式(11)和公式(9)中引入范數相關特征的必要性。作者使用的數據產生方式為:
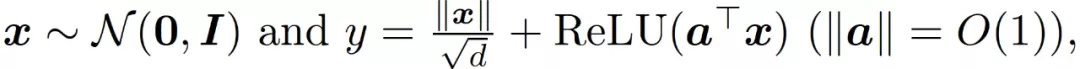
以及使用 ReLU 激活。圖 12 顯示,與簡單線性模型相比,f^lin 確實是一個更好的神經網絡近似。
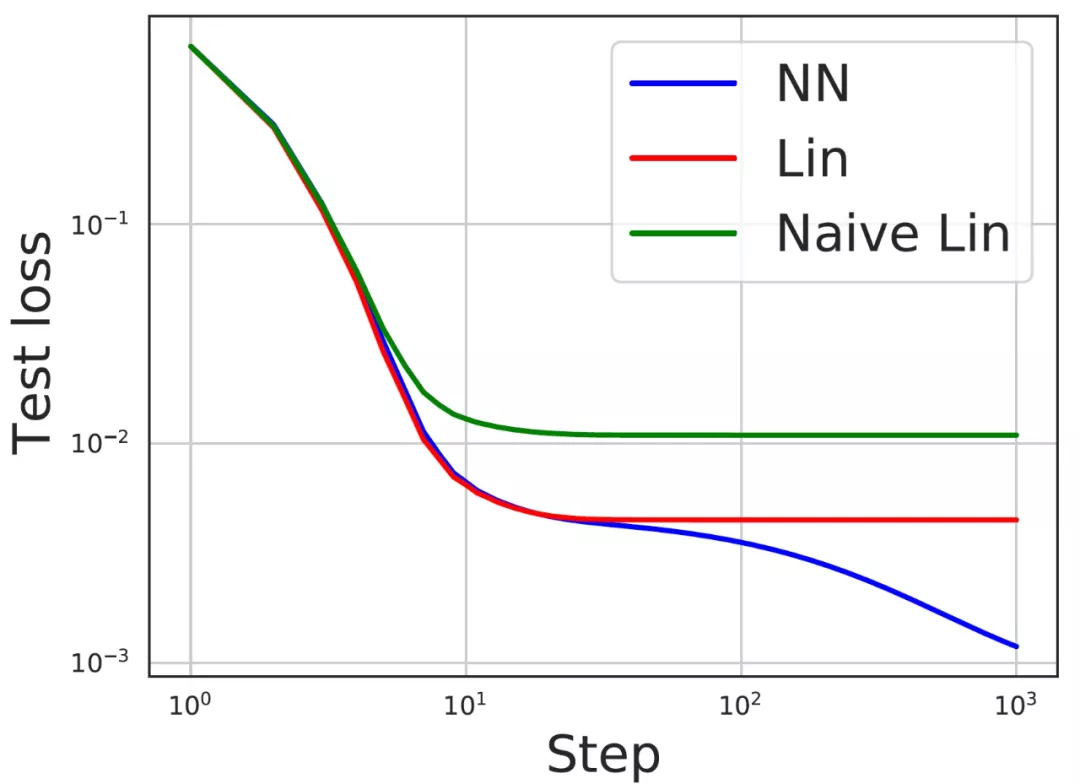
圖 12. 范數依賴性特征是非常必要的。對于學習范數依賴性函數的任務,測試損失顯示了具有 ReLU 激活的神經網絡,其相應的線性模型預測公式(11),以及通過重置公式(11)中ν_1 = ν_2 = 0 的線性模型。本文預測的線性模型是一個更好的神經網絡的近似。
3.3 擴展到多層和卷積神經網絡
最后,作者給出理論和實驗分析以證明神經網絡和線性模型在訓練早期階段的一致性可以擴展到更復雜的網絡架構和數據庫上。具體的,考慮一個簡單的一維 CNN,包含一個卷積層,沒有池化層:
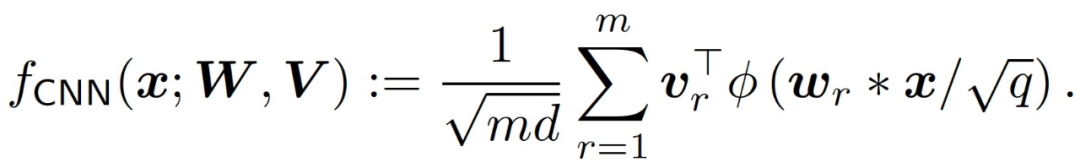
作者使用多層 FC 網絡和 CNN 對 CIFAR-10 的二元分類任務("cats" 與 "horses")進行了實驗。訓練和測試數據的數量分別是 10,000 和 2,000。圖像的原始大小為 32×32×3,使用 4×4 平均池化處理將圖像縮小為 8×8×3。作者將測試數據的預測殘差分解到 V_lin,即輸入所覆蓋的空間,以及它的補充 (V_lin)^⊥(維數為 2000d)。對于這兩個網絡,我們在圖 13 (a) 中觀察到,網絡和線性模型的測試損失在 1,000step 以內幾乎是相同的,之后網絡開始在 (V_lin)^⊥處改進。在圖 13 (b) 中,作者繪制了 3 個隨機測試數據的 logit 演變情況,并再次觀察到在早期訓練階段的良好一致性。圖 13 (c)繪制了網絡和線性模型之間的相對 MSE。我們觀察到,這兩個網絡的 MSE 在最初的 1000step 中是很小的,之后就會增長。
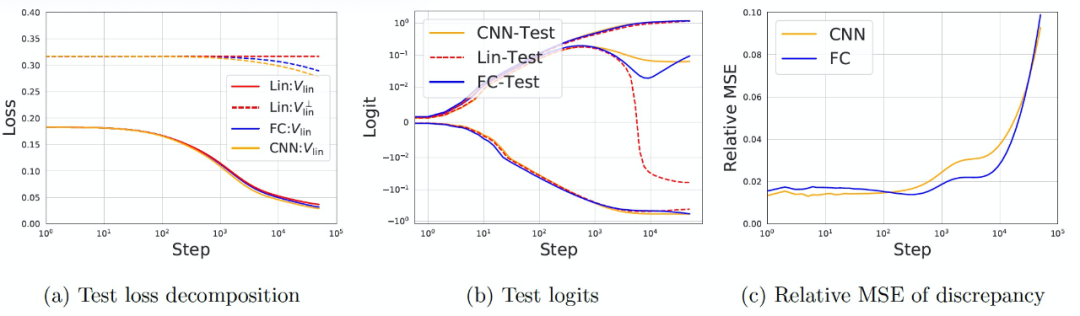
圖 13. 在早期訓練階段,4 個隱藏層的 CNN/FC 網絡與 CIFAR-10 的線性模型之間具有很好的一致性
4 液體的視覺感知:來自深度神經網絡的啟示 [3]

最后這篇文章的切入角度與前三篇不同,它提出了一個模仿人類視覺系統行為的前饋卷積網絡,作者具體分析了不同層次的網絡表征("virtual fMRI"),并研究了網絡容量(即單元數量)對內部表征的影響。
搞清大腦是如何在視覺上計算復雜的自然物質的物理特性的任務是視覺神經科學領域的一個重大挑戰。本文著重研究了液體的感知(the perception of liquids)—由于其極端的可變性和多樣化的行為,液體是一類特別具有挑戰性的材料。具體的,作者提出了一個可通過圖像計算的模型,該模型可以從流體模擬影片中預測人類的平均粘度判斷,也可以預測個體觀察者在各種觀察條件下的粘度判斷。作者訓練了一個人工神經網絡,從 10 萬個 20 幀的模擬中估計粘度,并發現這些模型在經歷相對較少的訓練步驟后(在它們達到最佳性能之前)就能很好地預測人類的感知。也就是說,在本文選擇的這一視覺神經科學的研究問題中,人工神經網絡也展現出了明顯的“早期關鍵學習期”的特征。這表明,雖然人類的粘度感知非常好,但理論上還可能有更好的表現。
此外,作者在文中使用 "虛擬電生理學 (virtual electrophysiology)" 深入分析網絡,揭示了網絡用于估計粘度的許多不同特征。作者發現這些特征受網絡參數空間大小的影響很大,但最終的預測性能幾乎沒有變化。這意味著在神經網絡模型和人類視覺系統之間進行直接推斷時需要非常謹慎。不過,本文介紹的方法還是能夠為比較人類和神經網絡提供一個可參考的系統性的框架。
4.1 問題背景介紹
幾個世紀以來,研究人員一直試圖解開人類視覺系統的工作機制—人類視覺系統能夠在難以想象的廣泛圖像中成功識別復雜、自然的物體和材料。其中,一個特別有趣的視覺能力是人類對液體的感知。液體可以展現出一系列不同的外觀,因為它們的形狀極易變化,既受內部物理參數的影響,如粘度,也受外部力量的影響,如重力。區分不同液體的最重要的物理特性是粘度。迄今為止,仍然沒有一個可通過圖像計算的模型能夠預測液體或其粘度的感知。本文作者嘗試利用深度神經網絡(DNNs)的最新進展來開發這樣一個模型,探測模型的內部運作機制以推斷出關于人類視覺系統如何刺激粘度的新假設。
在目前的機器學習中,大多數關于人工神經網絡的工作都集中在獲得在特定任務中的最佳性能。相比之下,本文的研究并不是開發一個在數學上最適合估計粘度的神經網絡,而是開發一個最接近于模仿人類視覺系統行為的前饋卷積網絡。為了評估模型與人類的相似程度,要求觀察者根據影片對粘度做出判斷,而這些影片也會直接展示給經過訓練的神經網絡以輸出判斷結果。
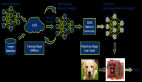
本文使用的神經網絡具有適用于處理影片數據的 "慢速融合(slow-fusion)" 架構(與靜態幀相對)[14]。在一個由計算機生成的流體模擬動畫影片的數據庫上訓練該模型,這些動畫影片長 20 幀,描述了液體在 10 個不同的場景類別中的互動,誘發了各種各樣的行為(傾倒、攪拌、灑落等,如圖 14 所示)。訓練目標是估計模擬中的物理粘度參數。為了測試通用性,作者在訓練期間未使用第十個場景(Scene 10),保留訓練階段中每個場景中 0.8% 的模擬動畫影片用來進行驗證。訓練標簽與模擬的 16 個不同的物理粘度步驟相對應。作為比較,人類觀察者執行了一項粘度評級任務,他們觀看了 800 個這些場景,并對場景分配了對應的感知粘度標簽。神經網絡是基于物理粘度標簽上訓練的,而不是人類的評分。但是,作者使用了貝葉斯優化網絡的超參數(例如,學習率,動量)和層的具體設置(核大小,過濾器的數量)來確定與人類在 800 個感知的粘度標簽上有良好關聯的網絡。訓練時間相對較短,只有 30 個 epochs(整個訓練庫的 30 次重復)。得到這些網絡后,作者分析了它們的內部表征,以確定導致類人行為的特征。

圖 14. 十個不同的 stimuli 場景。場景中模擬了不同的液體相互作用,如傾瀉、下雨、攪拌和浸泡。光學材料特性和照明圖是隨機分配的,白色平面和方形水庫保持不變。
作者的主要分析和發現如下。為了確定我們是否得到了一個足夠接近人類表現的模型,首先我們在逐個 stimuli 的基礎上比較了網絡的預測和人類的感知判斷。作者發現,為估計物理粘度而訓練的網絡確實能夠預測人類的平均粘度判斷,且與人類個體的判斷大致相同。人類就是這樣根據視覺 stimuli 展示來學習執行不同的視覺任務的,所以這樣一個在物理標簽和計算機模擬上訓練的網絡能夠預測人類的表現并不是一件非常簡單的事。作者還發現,經過早期訓練階段,網絡就能夠輸出很好的預測結果。
第二,在確定該網絡能夠模擬人類的表現后,作者試圖通過分析該網絡各個階段的單個單元的反應特性(虛擬電生理學)來深入了解該網絡的內部運作情況。具體做法是:(a)比較他們對一組手工設計的特征和真實場景屬性的反應,(b)確定最強烈或最弱地驅動單元的 stimuli,以及 (c) 通過激活最大化直接將特征可視化。這些分析表明,許多單元被調整為可解釋的時空和顏色特征。然而,作者也發現存在一組獨特的單元,這一組單元具有較復雜反應特性(即其反應很難被我們所考慮的任何特征所解釋),而這些單元對網絡的性能特別重要。作者的分析還表明,手工設計的特征的線性組合本身不足以解釋人類的粘度感知,這也進一步體現了額外單元的重要性。
第三,作者分析了整個層次的網絡表征("虛擬 fMRI"),并研究了網絡容量(即單元數量)對內部表征的影響。作者得出的主要結論有:(1) 沿著網絡的層次結構,從低層次的圖像描述符逐漸過渡到更高層次的特征,以及(2) 內部表征對單元數量的依賴程度與整體性能和預測人類判斷的能力無關。
最后,作者在整個網絡的層面上比較了表征以確認在同一數據庫上訓練的同一架構的 100 個實例是否產生了類似的內部表征(虛擬個體差異)。結果確實顯示出高度的相似性,但隨著網絡層次的加深相似性略有下降(即,低層次的表征在不同的網絡中幾乎是相同的,但是在訓練的后期階段的差異會增大)。作者還將本文模型與其他數據庫上(預)訓練的網絡架構進行了比較,發現在本文使用的特定訓練庫上訓練本文所使用的網絡架構可以產生與人類判斷最接近的判斷結果。
4.2 總體比較
4.2.1 人類的粘度評級
首先,作者嘗試確定在計算機模擬液體的過程中,為估計物理粘度參數而訓練的神經網絡是否能夠預測人類的主觀粘度判斷。為了做到這一點,作者首先測試了人類在粘度評級任務中的表現,以生成可與神經網絡進行比較的感知判斷。16 名觀察者分別對 800 部液體動畫影片的粘度進行評分,10 個場景類別中涵蓋了 16 個粘度等級。在每個場景類別中,用不同的隨機參數(如發射器速度、幾何體大小或不同的照明條件)模擬了五種變化。具體關于模擬的方法本文不再贅述,感興趣的讀者可以閱讀原文進行了解。粘度評分是通過 stimuli 物下方的反應滑塊完成的,允許觀察者報告每種液體的流動或粘稠程度。在訓練期間,觀察者會看到四個示例,其中包括最大和最小的粘度示例,以幫助他們確定他們的評級。
圖 15 給出了人類觀察員的結果(藍線)。在整個過程中,給出的報告數值是每個場景的五個變化中的平均值。一些場景(例如,場景 1)的表現明顯好于其他場景(例如,場景 4 和場景 6)。總的來說,物理粘度解釋了人類評分中 68% 的變異(R^2 = 0.68,F(1,158) = 337,p < .001)。
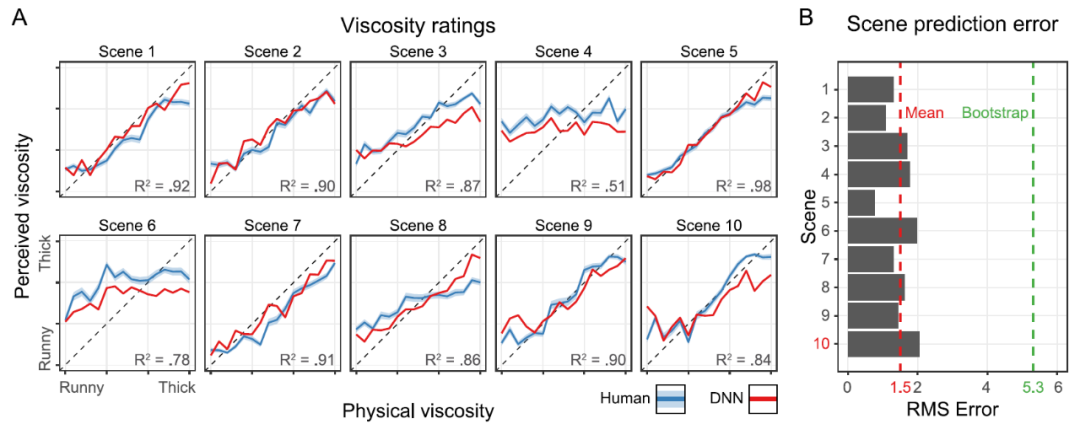
圖 15. (A) 10 個不同場景的粘度等級。X 軸顯示的是物理粘度等級(1-16)。y 軸顯示的是五個變化中的平均感知 / 預測的粘度。誤差帶顯示的是平均值的標準誤差(SEM)。藍線是人類的粘度評級,紅線是 DNN 的粘度預測。對角線上的虛線表示真實情況。DNN 沒有在這里預測的任何 stimuli 上進行訓練,場景 10(紅色)被完全排除在訓練庫之外,以測試對其他場景的通用性;(B) X 軸顯示了 Y 軸上 10 個場景中每個場景的均方根誤差。這是人類觀察和網絡預測之間的誤差。紅色虛線顯示的是各場景的平均誤差,綠色虛線顯示的是 1000 個隨機抽取的觀察結果的誤差。
4.2.2 網絡預測結果
在確定了人類在一系列條件下的表現后,我們接下來訓練神經網絡,目標是測試這種訓練是否能夠生成模仿人類判斷的成功和失敗模式的內部表征。具體網絡結構見圖 16。圖 15A 給出了一個神經網絡的預測結果(紅線)。總的來說,該模型在解釋物理粘度方面的表現與人類觀察者大致相同(R^2=0.73,F(1,158)=437,P<0.001)。重要的是,該網絡能很好地預測不同場景下粘度感知的差異。例如,像人類一樣,該網絡在場景 5 中表現良好,而在場景 4 中則表現不佳。因此,該模型正確地預測了人類感知的成功和失敗。事實上,網絡的預測和人類的平均判斷之間的 RMSE 只有 1.50 個粘度單位(圖 15B)。
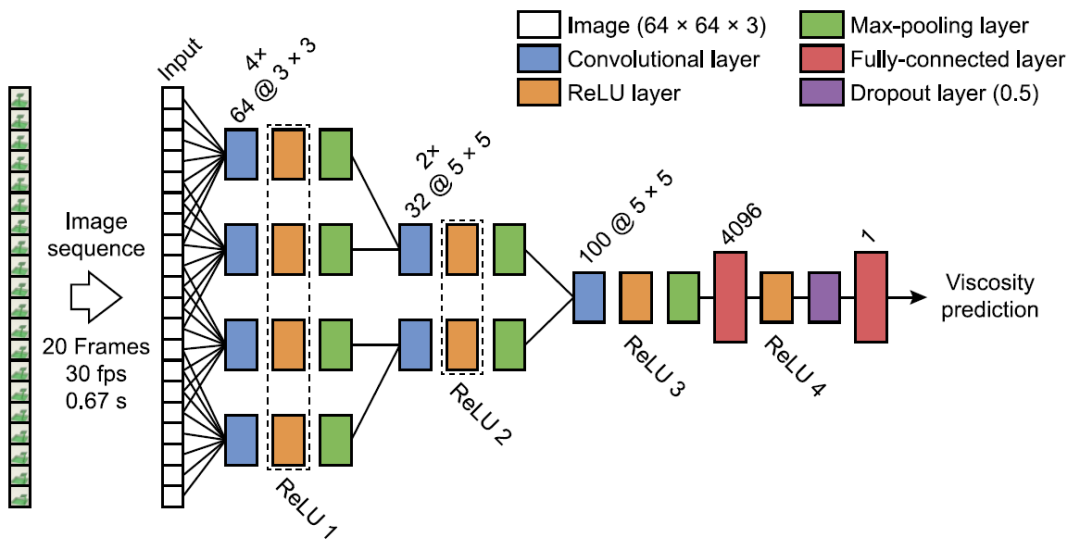
圖 16. 慢速融合網絡結構。輸入包括一個 20 幀的 64×64×3 圖像的動畫。包括三個連續的卷積階段,所有神經激活都是在 ReLU 層測量的,其中的響應被合并到 parallel layers。dropout 層在訓練期間以 50% 的概率將輸入元素隨機設置為零。
為了更好地了解網絡之間的可變性,作者訓練了 100 個相同的網絡實例,其中只有隨機初始化和訓練 stimuli 的隨機順序是不同的。作者表示,本文中使用的神經網絡是在誤差方面能最好地預測感知粘度的網絡。從圖 17 中的實驗結果可以看出,該網絡的不同實例具有非常相似的性能。
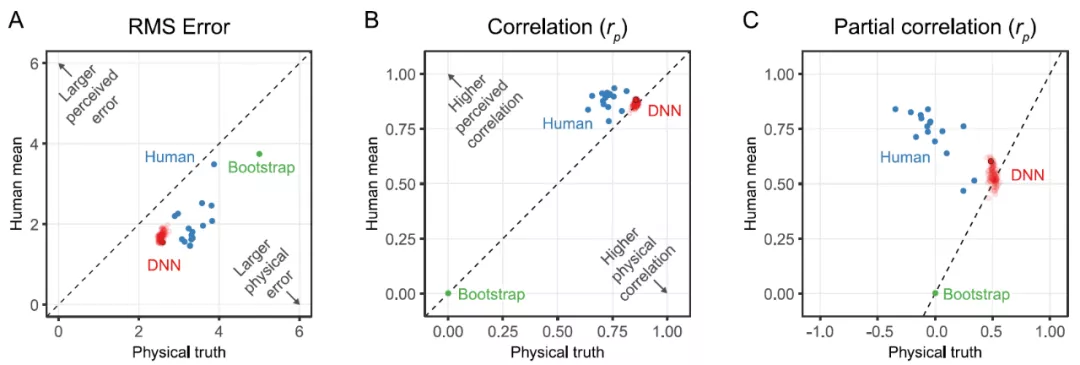
圖 17.(A)單個觀察者的均方根誤差(藍色),單獨訓練的 DNN 網絡中最終的網絡有一個黑色的輪廓(紅色),綠點顯示了基于 1000 次隨機抽樣的隨機性能的引導估計。如果數據點在圖的下半部分,則真值的誤差要大于人類的平均值或感知的粘度。(B)相同類型的圖表顯示了皮爾遜相關性(Pearson correlation)而不是 RMSE。在真值是控制變量的情況下,與人類平均值進行部分相關。如果數據點在圖的下半部分,則與真值的相關性大于人類平均值或感知粘度的相關性。(C)與 B 相同的圖,只有部分相關,其中對于物理真值,人類的平均值是一個顯示獨立相關性的控制變量。
粘度估計任務是非常具有挑戰性的,盡管如此,神經網絡仍然能夠捕獲人類判斷的一些核心特征的空間和時間圖像信息。有趣的是,進一步的訓練實際上降低了網絡預測人類感知粘度的能力(圖 18)。在早期訓練階段的 epoch 30 左右是一個關鍵時刻,之后過擬合開始增加(即藍色曲線與綠色曲線分離)。
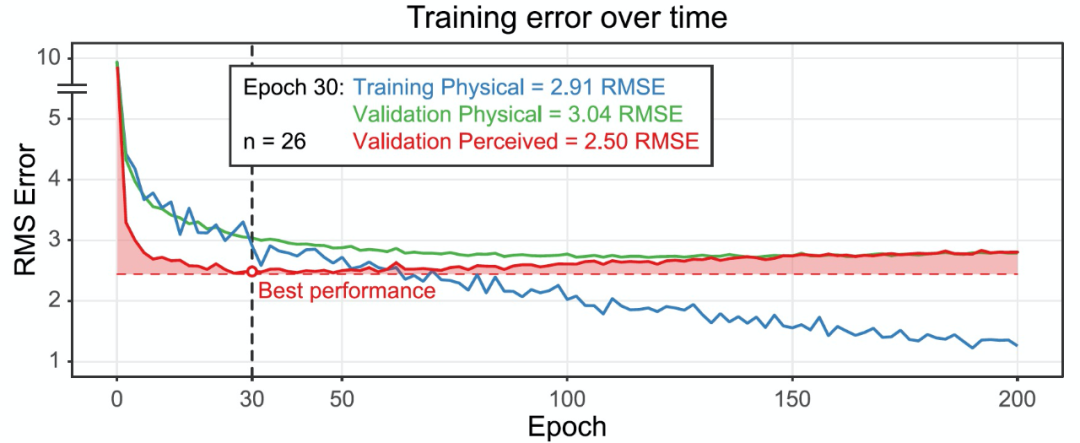
圖 18. 在 26 個單獨訓練的網絡中,隨著訓練時間的增加(X 軸),展示平均訓練和驗證誤差的變化(Y 軸)。本研究中使用的 100 個網絡只訓練了 30 個 epochs,因為隨著訓練的繼續,感知的粘度預測誤差會增加。
由上述分析,作者表示本文開發了一個圖像可計算模型,實現了在一個具有挑戰性的材料感知任務中預測人類的感知。特別是,開發這種模型的一種方法是用數萬部影片訓練神經網絡來估計 ground-truth 物理粘度,同時通過貝葉斯優化來優化網絡的超參數,使預測 800 個實驗 stimuli 物的感知粘度的誤差最小。此外,作者發現,通過相對較短的 30 個 epochs 的訓練即可獲得很好的訓練結果,此后進一步的訓練則會降低性能。作者表示,這一發現可以幫助克服 “只有擁有足夠的標記數據才能訓練模型” 的挑戰,并允許我們測試特定的學習目標和訓練庫在人類表現中的作用。
4.3 神經活動
在確定這些網絡能夠為人類的感知判斷提供了一個很好的模型之后,作者接下來研究它們的內部運作方式。具體來說,為了更好地了解網絡所進行的計算,作者對單元級(unit-level)和層級(layer-level)的激活進行了表征相似性分析(Representational
Similarity Analysis,RSA),并進行了網絡間激活的比較(Centred Kernel Alignment,CKA)。
為了得到與網絡反應的詳細情況相關的信息(類似于單細胞電生理學)作者在單個單元的水平上進行了 RSA,映射出網絡中的每個單元如何代表所有 800 個實驗 stimuli 之間的關系,并將這些與基于圖像和高級預測器進行比較(圖 19A)。具體來說,對于 800 個 stimuli 中的每一個 stimuli,作者從網絡中收集單個單元的神經激活模式;從每個影片中計算出的圖像特征值;以及與每個 stimuli 相關的高級特征(例如,感知的粘度、場景標簽,圖 19B)。計算 800 個 stimuli 中的每一個與所有其它 stimuli 之間的差異,并存儲在一個表征差異矩陣(Representational Dissimilarity Matrix,RDM;圖 19C)中。然后,我們衡量每個圖像特征的 RDM 與來自網絡中特定單元的 RDM 之間的關聯程度。對于卷積層中的每個單元,在 18 維的預測器空間中都有一個對應的位置。圖 19D 顯示了四個示例單元的 18 個預測器的一個子集,以及預測器的 RDM 和一個單元的激活 RDM 之間的相關性。為了更清楚地了解單元的具體功能,我們將最小和最大限度地激活單元的 stimuli 可視化展示(如圖 19E)。
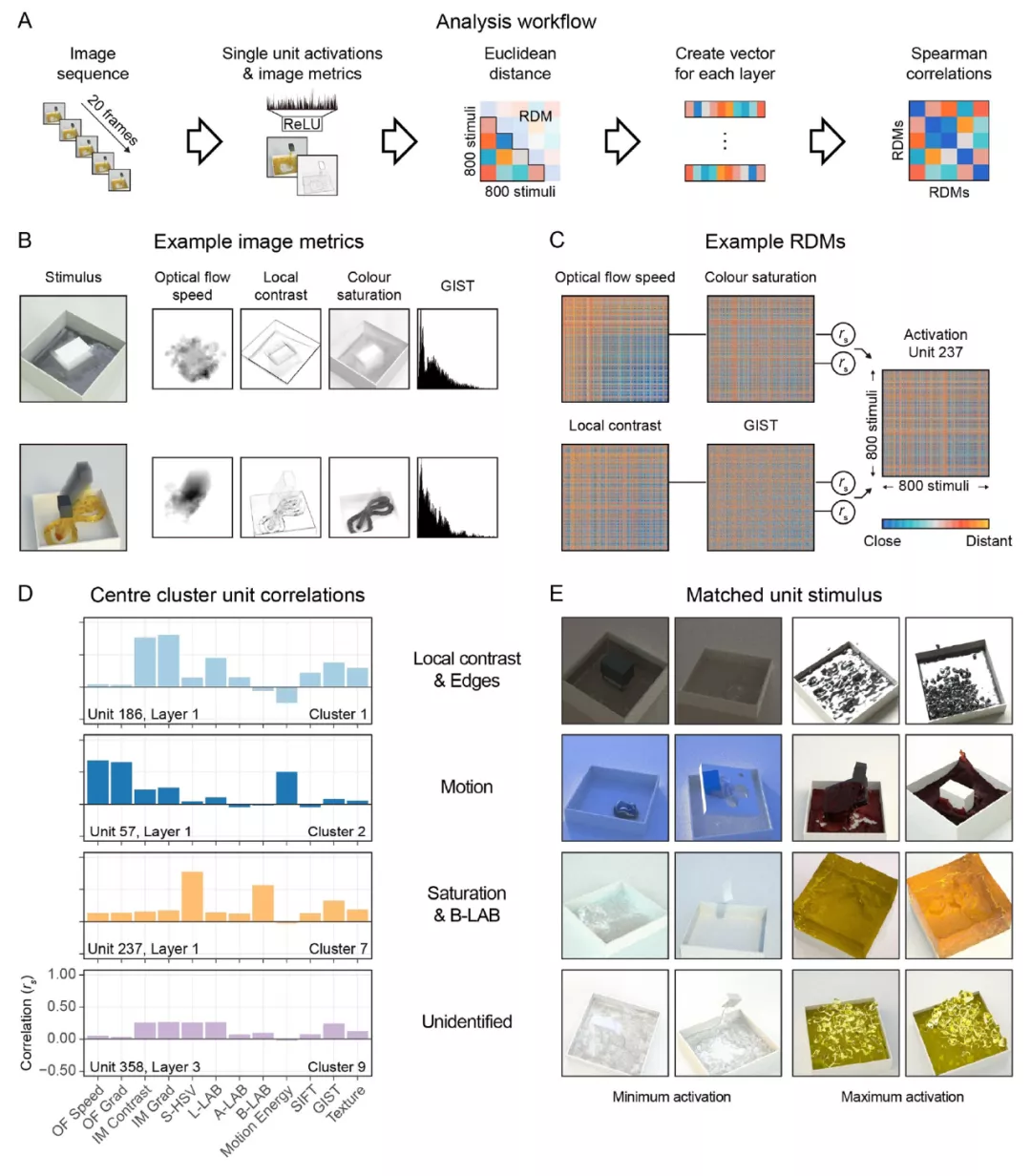
圖 19.(A) 單元級分析的 RSA 工作流程。(B) 兩個 stimuli 與所產生的圖像度量輸出的示例。重影效應(the ghosting effect)顯示了隨時間變化的運動。多特征指標,如運動能量和 GIST,失去了空間結構。(C)與 B 相同的圖像指標的 RDM 實例。每行 / 列代表一個 stimuli,顏色表示每對 stimuli 之間在相應圖像指標方面的距離。每個 RDM 都與單個單元的激活 RDM 相關,在本例中是 Unit237。(D) 最接近四個群組中心的單元的 RSA 相關性的選擇。整個數據庫中的兩個 stimuli 為 D 的單元創造了最小和最大的激活反應。
為進一步了解驅動單個單元活動的因素,作者應用激活最大化來可視化每個單元的響應函數(圖 20)。慢速融合結構的平行通路(parallel pathways)允許每條通路捕獲特定時間的特征。這種關于時間和空間信息的自由的編碼方式,加上較小的內核,產生的可視化結果往往是抽象的和難以解釋的。第 1 層和第 2 層有不同的時間長度,可部分訪問完整的圖像序列(即 L1=8 幀,L2=12 幀,L3 和 L4=20 幀的完整序列)。根據視覺檢查,我們發現第一層主要包含不同時間頻率和方向的簡單運動相關特征。顏色起了一些作用,不同程度的亮度也被編碼。第二層的特征編碼了一系列具有時間和顏色變化的紋理,包括具有不同方向的脈動和流動的空間 - 時間紋理。在第 3 層,特征包括不同空間和時間位置的強烈對比的紋理。然而,反應變得越來越抽象,很難想象這樣的單元是真正預測粘度的,這也表明了表征是高度分布的(即依賴許多單元的群體活動,而不是特定粘度或流動模式的 "祖母細胞(grandmother cells)")。全連接的第 4 層的視覺效果主要描述了具有時間上重復出現的顏色模式的噪聲斑塊,這些顏色模式在各單元之間是同步的。這種同步性也發生在不同的種子圖像上,表明這些顏色的敏感性在第 4 層的各個單元中都有類似的編碼。針對這一現象,作者提出了一個問題:時間上的顏色序列是否可能是網絡功能的一個重要線索?我們都知道,對于人類來說粘度感知在很大程度上與顏色無關。不過,繼續實驗我們發現,當我們使用灰度 stimuli 時,網絡的預測誤差只增加了 7%。這表明顏色只為粘度估計提供了有限的信息。因此,作者表示,第 4 層各單元的顏色敏感性的同步時間波動仍然難以解釋。

圖 20. 每個層的激活最大化結果的靜態快照。全連接層 4(FC4)有 4096 個單元,隨機挑選了 100 個單元用于此圖。
最后,聚焦到我們這篇文章討論的深度學習中的關鍵學習期問題,本文網絡只訓練了 30 個 epochs,這是一個相對較短的時間。作者發現,在第 30 個 epoch 之后,感知到的粘度預測結果越來越差,網絡開始過擬合。在第 30 個 epoch 后,帶有物理粘度標簽的訓練誤差和帶有物理粘度標簽的驗證誤差之間的差異越來越大。
作者討論了這一發現的原因和意義。作者首先猜測,人類的表現與訓練的關系是呈 U 型近似的。不過,作者說這可能只是本文所用的訓練庫上展示出來的一個假象。這里考慮的模型完全是在計算機模擬的液體中訓練的,雖然在本文給出的模擬環境中成功的模擬了人類的學習能力,但是在更多的、更大的或自然的訓練數據中,可能會隨著訓練的持續反而提高對人類性能的近似能力(即不會觀察到對人類性能的 U 形近似),也即與本文提出的關鍵學習期并不吻合。
作者也提出了另一種可能性,即我們這篇文章討論的 “關鍵學習期” 的存在。人類觀察者使用的線索是那些網絡也傾向于首先學習的線索。有可能這些線索是數據庫中最容易辨別或最穩健的線索。隨著訓練的繼續,網絡在物理粘度估計目標方面繼續改進,可能是通過學習數據庫中特有的更微妙的線索來實現,而人類視覺系統根本無法辨別或對這些線索不太敏感。神經網絡學習的早期階段的其它研究也發現,關鍵的學習期與生物網絡相似[1],有證據表明,在訓練早期階段,神經連接大致上處于記憶形成階段,此后神經可塑性下降,只有通過重組或遺忘較少的預測性權重而發生小得多的變化。這使得早期階段(<10 epoch)成為一個特別關鍵的時期,這一時期完成對數據庫中最主要的信息的編碼。在本文的案例中,這一時期的定義是感知到的粘度誤差下降特別大。這與我們的猜測一致,即在早期訓練中編碼的最明顯的線索與人類使用的感知粘度線索一致。
5 小結
本文討論了深度學習中的關鍵學習期問題,即在深度神經網絡的訓練過程中,早期階段與其它階段具有不同的 “特點”。第 2-4 篇文章從不同的角度證實了 DNNs 中可能確實存在“關鍵學習期”,當然這種“關鍵學習期” 可能僅僅展示為線性 / 非線性性能的不同,也可能展示為模型學習能力的不同。
在我們參考引用的文章中,給出了大量的、角度不同的實驗結果展示深度神經網絡中 “關鍵學習期” 的存在。不過,幾位作者在文中都表示了,確實沒有確切的、可推廣的理論分析以支撐普遍的關鍵學習期存在且發揮作用的說法。甚至如第四篇文章作者猜測,模型的性能有可能最終展示為 U 型,即,在大量的、自然的、高質量的數據存在的情況下,是否有可能在不斷訓練的后期性能反而提升?而目前看到的 “關鍵學習期” 可能還是訓練數據本身的質量受限所造成的?
深度學習中的關鍵學習期問題還是一個開放性的問題,我們也會在以后的文章中關注這一領域的研究進展,希望能夠在實現模型性能提升的同時,慢慢地發現和了解模型的內在的特性。
本文參考引用的文獻
[1] Alessandro Achille, Matteo Rovere, Stefano Soatto, CRITICAL LEARNING PERIODS IN DEEP NETWORKS, ICLR 2019., https://arxiv.org/abs/1711.08856
[2] Takao K Hensch. Critical period regulation. Annual review of neuroscience, 27:549–579, 2004.
[3] van Assen JJR, Nishida S, Fleming RW (2020) Visual perception of liquids: Insights from deep neural networks. PLoS Comput Biol 16(8): e1008018. https://doi.org/10.1371/journal.pcbi.1008018
[4] Hu W , Xiao L , Adlam B , et al. The Surprising Simplicity of the Early-Time Learning Dynamics of Neural Networks. arXiv e-prints, 2020. https://arxiv.org/abs/2006.14599
[5] Jastrzebski S , Szymczak M , Fort S , et al. The Break-Even Point on Optimization Trajectories of Deep Neural Networks. ICLR 2020.https://arxiv.org/abs/2002.09572
[6] David Taylor et al. Critical period for deprivation amblyopia in children. Transactions of the ophthalmological societies of the United Kingdom, 99(3):432–439, 1979.
[7] Donald E Mitchell. The extent of visual recovery from early monocular or binocular visual deprivation in kittens. The Journal of physiology, 395(1):639–660, 1988.
[8] Pasko Rakic, Jean-Pierre Bourgeois, Maryellen F Eckenhoff, Nada Zecevic, and Patricia S Goldman-Rakic. Concurrent overproduction of synapses in diverse regions of the primate cerebral cortex. Science, 232(4747):232–235, 1986.
[9] Ravid Shwartz-Ziv and Naftali Tishby. Opening the black box of deep neural networks via information. arXiv preprint arXiv:1703.00810, 2017.
[10] Gr´egoire Montavon, Mikio L Braun, and Klaus-Robert M¨uller. Kernel analysis of deep networks. Journal of Machine Learning Research, 12(Sep):2563–2581, 2011.
[11] Eric I Knudsen. Sensitive periods in the development of the brain and behavior. Journal of cognitive neuroscience, 16(8):1412–1425, 2004.
[12] Dumitru Erhan, Yoshua Bengio, Aaron Courville, Pierre-Antoine Manzagol, Pascal Vincent, and Samy Bengio. Why does unsupervised pre-training help deep learning? Journal of Machine Learning Research, 11(Feb):625–660, 2010.
[13] Greg Yang, Jeffrey Pennington, Vinay Rao, Jascha Sohl-Dickstein, and Samuel S. Schoenholz. A mean field theory of batch normalization. CoRR, abs/1902.08129, 2019.
[14] Karpathy A, Toderici G, Shetty S, Leung T, Sukthankar R, Fei-Fei L. Large-scale video classification with convolutional neural networks. In: Proceedings of the IEEE conference on Computer Vision and Pattern Recognition. 2014. p. 1725–1732.