革新Transformer!清華大學提出全新骨干網絡長時序預測達到SOTA
盡可能延長預測時效是時序預測的核心難題,對于能源、交通、經濟的長期規劃,氣象災害、疾病的早期預警等具有重要意義。
清華大學軟件學院機器學習實驗室的研究人員近日發表了一篇論文,探究了在信息有限的情況下預測更長期未來的這個難題。
針對上述問題,作者大刀闊斧革新Transformer,提出全新的Autoformer模型,在長時序預測方面達到SOTA,在效率性能上均超過Transformer及其變體。

論文鏈接:
https://arxiv.org/abs/2106.13008
研究背景
雖然近期基于Transformer的模型在時序預測上取得了一系列進展,但是Transformer的固有設計,使得在應對長期序列時仍存在不足:
- 隨著預測時效的延長,直接使用自注意力(self-attention)機制難以從復雜時間模式中找到可靠的時序依賴。
- 由于自注意力的二次復雜度問題,模型不得不使用其稀疏版本,但會限制信息利用效率,影響預測效果。
作者受到時序分析經典方法和隨機過程經典理論的啟發,重新設計模型,打破Transformer原有架構,得到Autoformer模型:
- 深度分解架構:突破將時序分解作為預處理的傳統方法,設計序列分解單元以嵌入深度模型,實現漸進式地(progressively)預測,逐步得到可預測性更強的組分。
- 自相關(Auto-Correlation)機制:基于隨機過程理論,丟棄點向(point-wise)連接的自注意力機制,實現序列級(series-wise)連接的自相關機制,且具有的復雜度,打破信息利用瓶頸。
- 應對長期預測問題,Autoformer在能源、交通、經濟、氣象、疾病五大領域取得了38%的大幅效果提升。
方法介紹
作者提出了Autoformer模型,其中包括內部的序列分解單元、自相關機制以及對應的編碼器、解碼器。
(1)深度分解架構
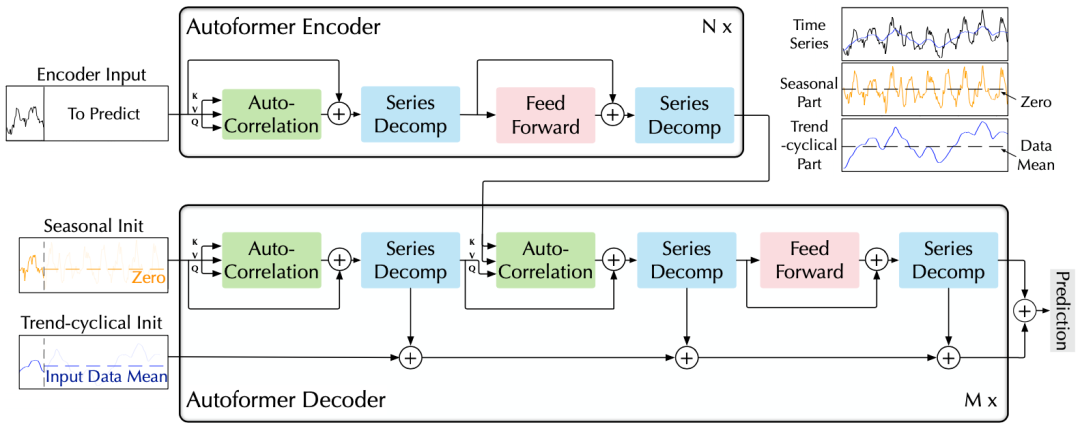
Autoformer架構
時間序列分解是時序分析的經典方法,可以將時間序列分解為幾類潛在的時間模式,如周期項,趨勢項等。
在預測任務中,由于未來的不可知性,通常先對輸入進行分解,再每個組分分別預測。
但這樣使得預測結果受限于分解效果,并且忽視了長期未來中各個組分之間的相互作用。
針對上述問題,作者提出深度分解架構,在預測過程中,逐步從隱變量中分離趨勢項與周期項,實現漸進式(progressive)分解。
并且模型交替進行預測結果優化和序列分解,可以實現兩者的相互促進。
A. 序列分解單元
基于滑動平均思想,平滑時間序列,分離周期項與趨勢項:
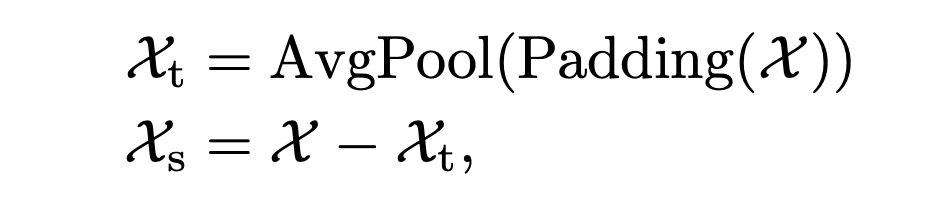
其中,為待分解的隱變量,分別為趨勢項和周期項,將上述公式記為。
B. 編解碼器
編碼器:通過上述分解單元,模型可以分離出周期項,。而基于這種周期性,進一步使用自相關機制(),聚合不同周期的相似子過程:

解碼器:對趨勢項與周期項分別預測。
- 對于周期項,使用自相關機制,基于序列的周期性質來進行依賴挖掘,并聚合具有相似過程的子序列;
- 對于趨勢項,使用累積的方式,逐步從預測的隱變量中提取出趨勢信息。

(2)自相關機制
觀察到,不同周期的相似相位之間通常表現出相似的子過程,利用這種序列固有的周期性來設計自相關機制,實現高效的序列級連接。
自相關機制包含基于周期的依賴發現(Period-based dependencies)和時延信息聚合(Time delay aggregation)。
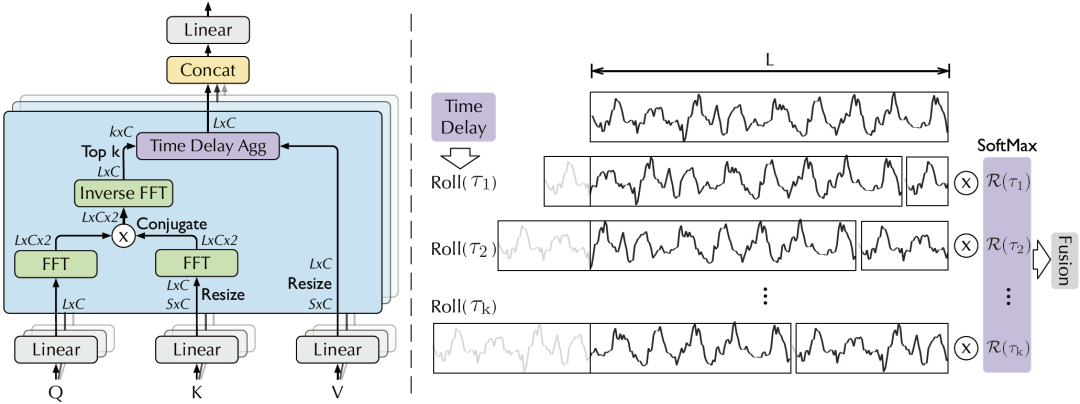
自相關機制,右側為時延信息聚合
A. 基于周期的依賴發現
基于上述觀察,為找到相似子過程,需要估計序列的周期。基于隨機過程理論,對于實離散時間過程,可以如下計算其自相關系數:
其中,自相關系數表示序列與它的延遲之間的相似性。
在自相關機制中,將這種時延相似性看作未歸一化的周期估計的置信度,即周期長度為的置信度為。
實際上,基于Wiener-Khinchin理論,自相關系數可以使用快速傅立葉變換(FFT)得到,其計算過程如下:
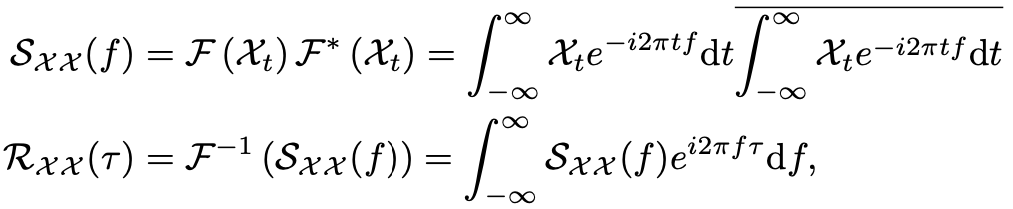
其中,和分別表示FFT和其逆變換。因此,復雜度為。
B. 時延信息聚合
為了實現序列級連接,還需要將相似的子序列信息進行聚合。自相關機制依據估計出的周期長度,首先使用操作進行信息對齊,再進行信息聚合:
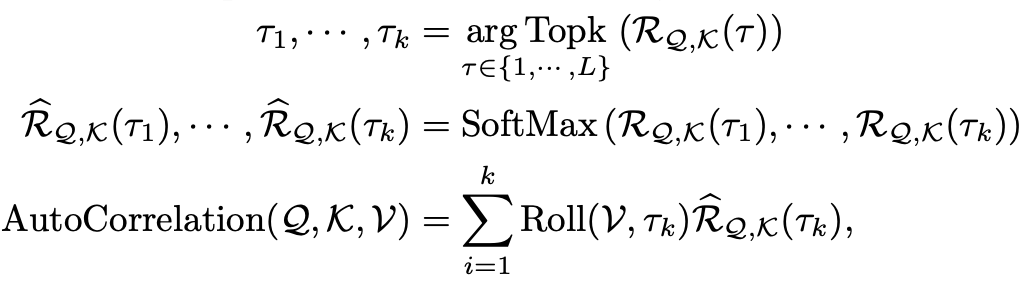
這里,依然使用query、key、value的多頭形式,從而可以無縫替換自注意力機制。
同時,挑選最有可能的個周期長度,用于避免融合無關、甚至相反的相位。整個自相關機制的復雜度仍為。
C. 對比分析
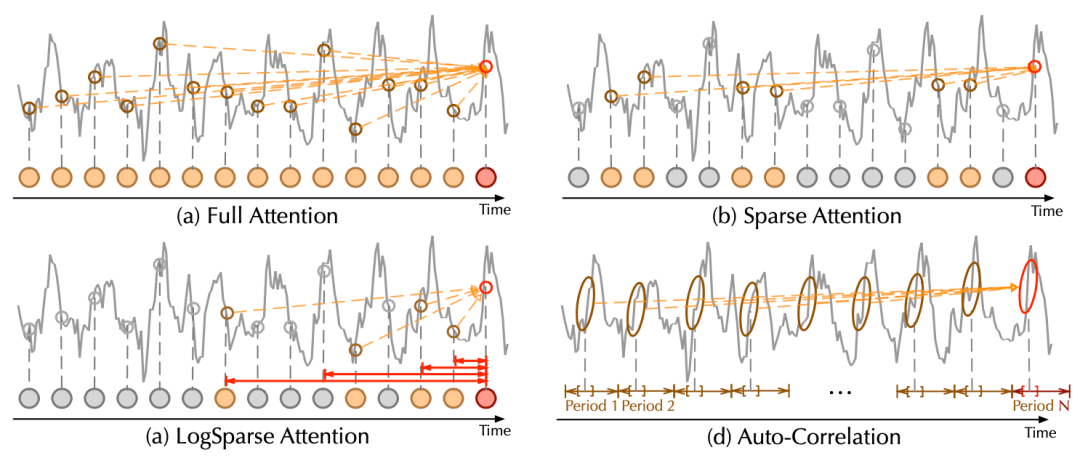
自相關機制與自注意力機制對比
相比于之前的點向連接的注意力機制或者其稀疏變體,自注意力(Auto-Correlation)機制實現了序列級的高效連接,從而可以更好的進行信息聚合,打破了信息利用瓶頸。
實驗
作者在6個數據集上進行了測試,涵蓋能源、交通、經濟、氣象、疾病五大主流領域。
(1) 主要結果
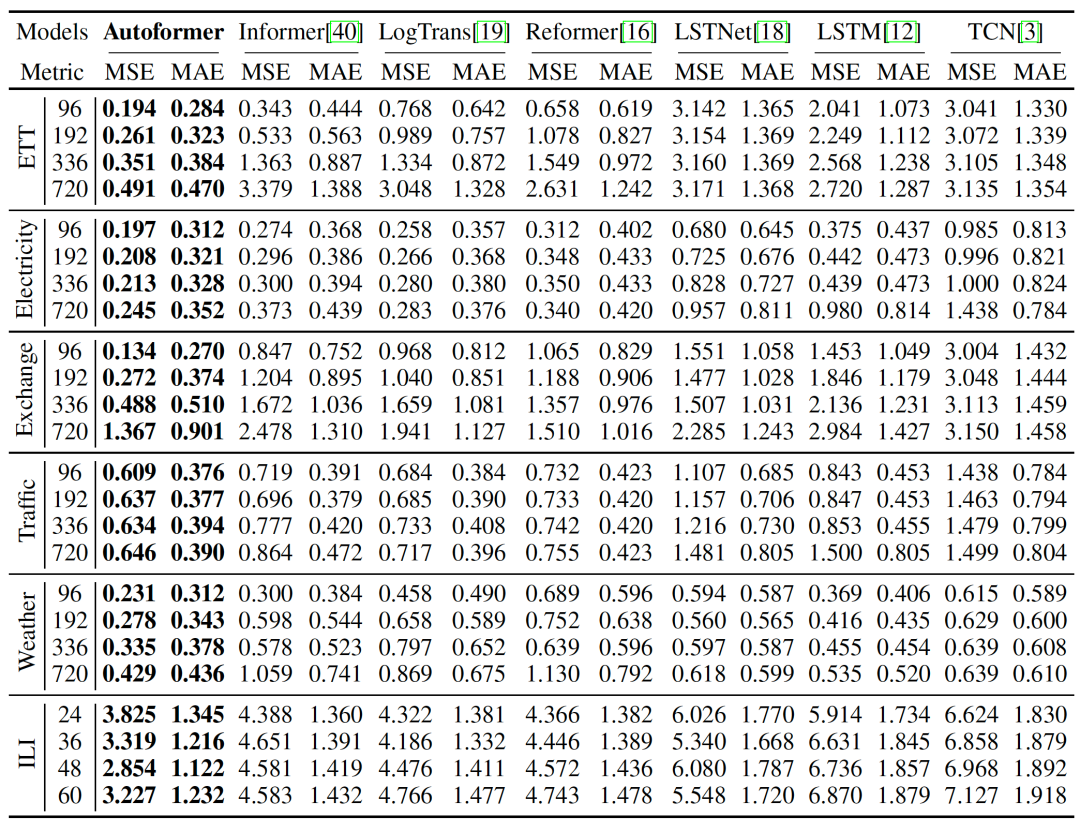
整體實驗結果
Autoformer在多個領域的數據集、各種輸入-輸出長度的設置下,取得了一致的最優(SOTA)結果。
在input-96-predict-336設置下,相比于之前的SOTA結果,Autoformer實現了ETT能源數據集74%的MSE提升,Electricity能源數據集MSE提升24%,Exchange經濟數據集提升64%,Traffic交通數據集提升14%,Weather氣象數據集提升26%,在input-24-predict-60設置下,ILI疾病數據集提升30%。
在上述6個數據集,Autoformer在MSE指標上平均提升38%。
(2) 對比實驗
深度分解架構的通用性:將提出的深度分解架構應用于其他基于Transformer的模型,均可以得到明顯提升,驗證了架構的通用性。
同時隨著預測時效的延長,提升效果更加明顯,這也印證了復雜時間模式是長期預測的核心問題。
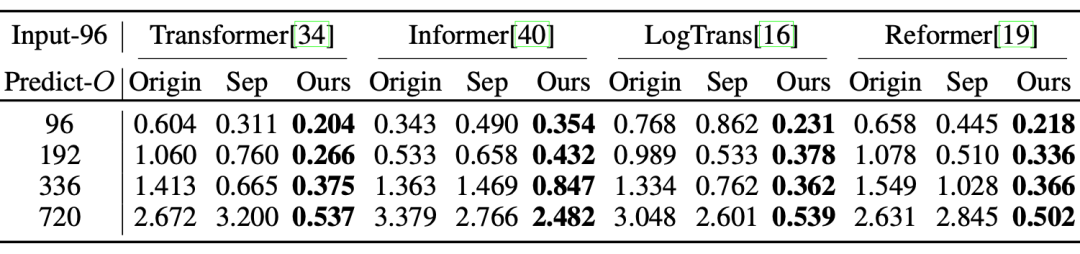
ETT數據集上的MSE指標對比,Origin表示直接預測,Sep表示先分解后預測,Ours表示深度分解架構。
自相關機制 vs. 自注意力機制:同樣基于深度分解架構,在眾多輸入-輸出設置下,自相關機制一致優于自注意力機制及其變體,比如經典Transformer中的Full Attention,Informer中的PropSparse Attention等。
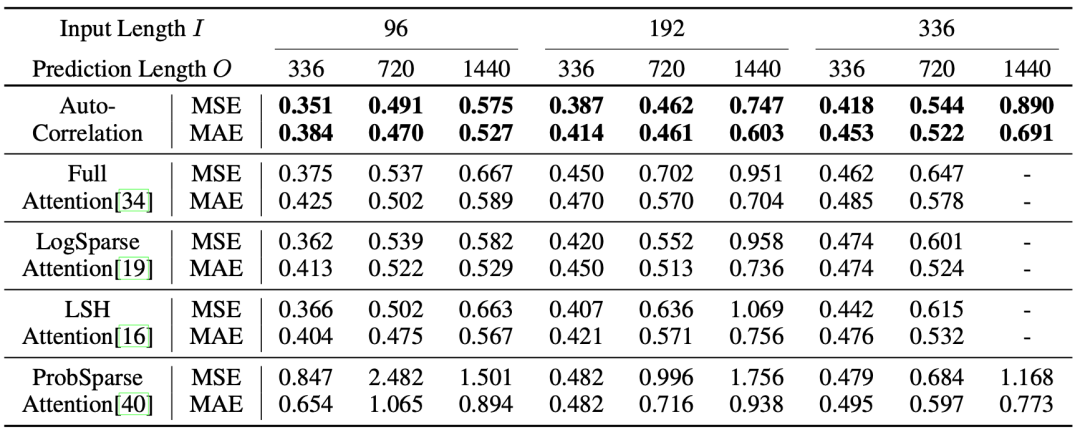
ETT數據集上對比實驗,將Autoformer中的自相關機制替換為其他自注意力機制,得到上述結果。
(3) 模型分析
時序依賴可視化:
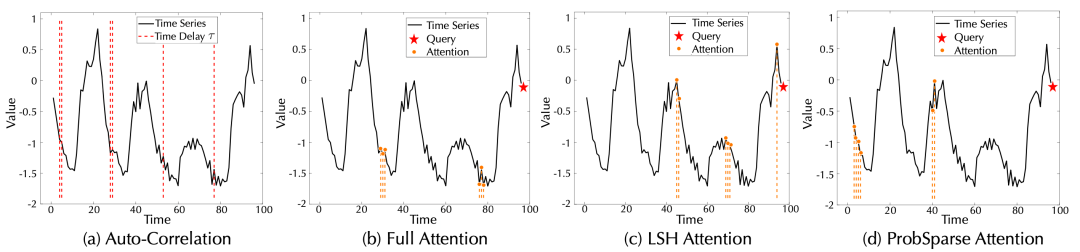
對于序列的最后一個時間點,各模型學到的時序依賴可視化,圖(a)中紅色線表示學習到的過程的位置。
通過上圖可以驗證,Autoformer中自相關機制可以正確發掘出每個周期中的下降過程,并且沒有誤識別和漏識別,而其他注意力機制存在缺漏甚至錯誤的情況。
效率分析:
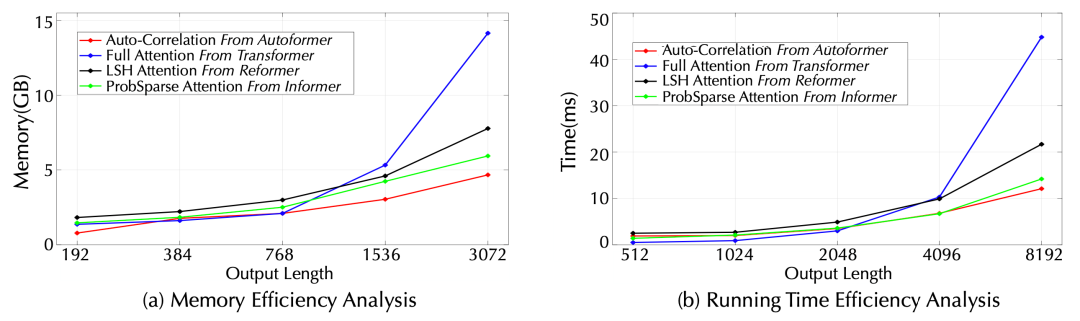
效率對比,紅色線為自相關機制
在顯存占用和運行時間兩個指標上,自相關機制均表現出了優秀的空間、時間效率,兩個層面均超過自注意力機制及其稀疏變體,表現出高效的復雜度。
總結
針對長時序列預測中的問題,作者基于時序分析的經典方法和隨機過程的經典理論,提出了基于深度分解架構和自相關機制的Autoformer模型。
Autoformer通過漸進式分解和序列級連接,應對復雜時間模式以及信息利用瓶頸,大幅提高了長時預測效果。
同時,Autoformer在五大主流領域均表現出了優秀的長時預測結果,模型具有良好的效果魯棒性,具有很強的應用落地價值。