成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

Python實現之初等函數一

作者：一只小小鳥鳥
開發 后端
初等函數是由基本初等函數經過有限次的四則運算和復合運算所得到的函數。基本初等函數和初等函數在其定義區間內均為連續函數。高等數學將基本初等函數歸為五類：冪函數、指數函數、對數函數、三角函數、反三角函數。

[[413349]]

本文轉載自微信公眾號「python與大數據分析」，作者一只小小鳥鳥。轉載本文請聯系python與大數據分析公眾號。

初等函數是由基本初等函數經過有限次的四則運算和復合運算所得到的函數。基本初等函數和初等函數在其定義區間內均為連續函數。高等數學將基本初等函數歸為五類：冪函數、指數函數、對數函數、三角函數、反三角函數。

比較頭疼的是numpy中的冪函數不支持負數定義域，所以找了很多辦法來解決該問題。

主函數代碼如下：

  1. #!/usr/bin/env python 
  2. # -*- coding: UTF-8 -*- 
  3. #                     _ooOoo_ 
  4. #                   o8888888o 
  5. #                    88" . "88 
  6. #                 ( | -  _  - | ) 
  7. #                     O\ = /O 
  8. #                 ____/`---'\____ 
  9. #                  .' \\| |// `. 
  10. #                 / \\|||:|||// \ 
  11. #               / _|||||-:- |||||- \ 
  12. #                | | \\\ - /// | | 
  13. #              | \_| ''\---/'' | _/ | 
  14. #               \ .-\__ `-` ___/-. / 
  15. #            ___`. .' /--.--\ `. . __ 
  16. #         ."" '< `.___\_<|>_/___.' >'"". 
  17. #       | | : `- \`.;`\  _ /`;.`/ - ` : | | 
  18. #          \ \ `-. \_ __\ /__ _/ .-` / / 
  19. #      ==`-.____`-.___\_____/___.-`____.-'== 
  20. #                     `=---=' 
  21. ''' 
  22. @Project ：pythonalgorithms  
  23. @File ：basicfunction.py 
  24. @Author ：不勝人生一場醉 
  25. @Date ：2021/7/19 17:39  
  26. ''' 
  27. import matplotlib.pyplot as plt 
  28. import numpy as np 
  29. import math 
  30. import mpl_toolkits.axisartist as axisartist  # 導入坐標軸加工模塊 
  31.  
  32.  
  33. # -----------------函數------------------ 
  34. # 給定一個數集A，對A施加一個對應的法則/映射f，記做:f(A)，那么可以得到另外一個數集B，也就是可以認為B=f(A)； 
  35. # 那么這個關系就叫做函數關系式，簡稱函數。 
  36. # 三個重要的因素: 定義域A、值域B、對應的映射法則f。 
  37.  
  38.  
  39. if __name__ == "__main__": 
  40.     # 一次函數 
  41.     Linearfunction() 
  42.     # 二次函數 
  43.     Quadraticfunction() 
  44.     # 冪函數 
  45.     powerfunction() 
  46.     # 指數函數 
  47.     exponentialfunction() 
  48.     # 對數函數 
  49.     Logarithmicfunction() 

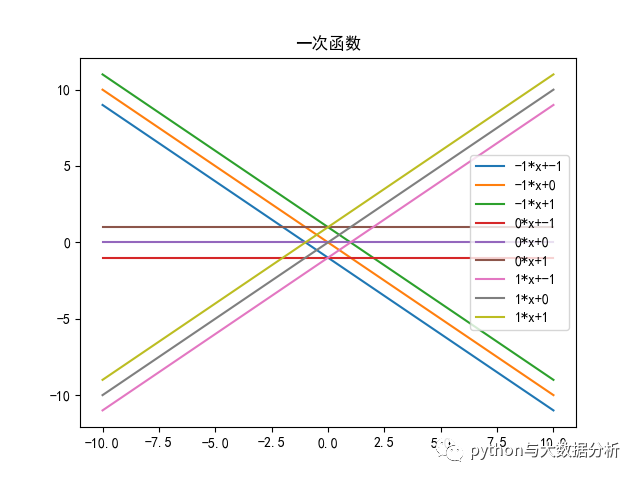
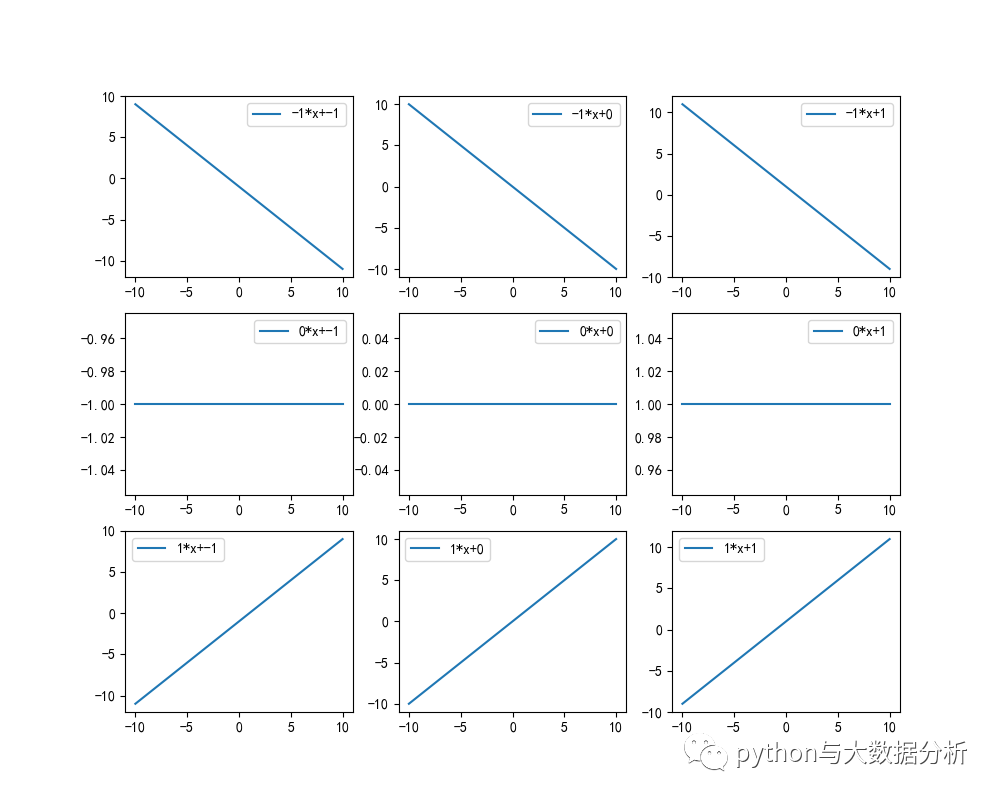
一次函數代碼如下：

  1. # ---------------一次函數------------------ 
  2. # 一次函數是函數中的一種，一般形如y=ax+b（a，b是常數，a≠0），其中x是自變量，y是因變量。 
  3. # 當b=0時，y=kx（k為常數，k≠0），y叫做x的正比例函數 
  4. # 當a=0時，y=b，則為常函數 
  5. def Linearfunction(): 
  6.     fig = plt.figure(figsize=(10, 8)) 
  7.     plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  8.     plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  9.     x = np.linspace(-10, 10, 100) 
  10.     i = 1 
  11.     alist = [-1, 0, 1] 
  12.     blist = [-1, 0, 1] 
  13.     for a in alist: 
  14.         for b in blist: 
  15.             plt.subplot(3, 3, i) 
  16.             y = x * a + b 
  17.             label = '{}*x+{}'.format(a, b) 
  18.             plt.plot(x, y, label=label) 
  19.             plt.legend() 
  20.             i += 1 
  21.     plt.show() 
  22.  
  23.     for a in alist: 
  24.         for b in blist: 
  25.             y = x * a + b 
  26.             label = '{}*x+{}'.format(a, b) 
  27.             plt.plot(x, y, label=label) 
  28.             i += 1 
  29.     plt.title("一次函數") 
  30.     plt.legend() 
  31.     plt.show() 

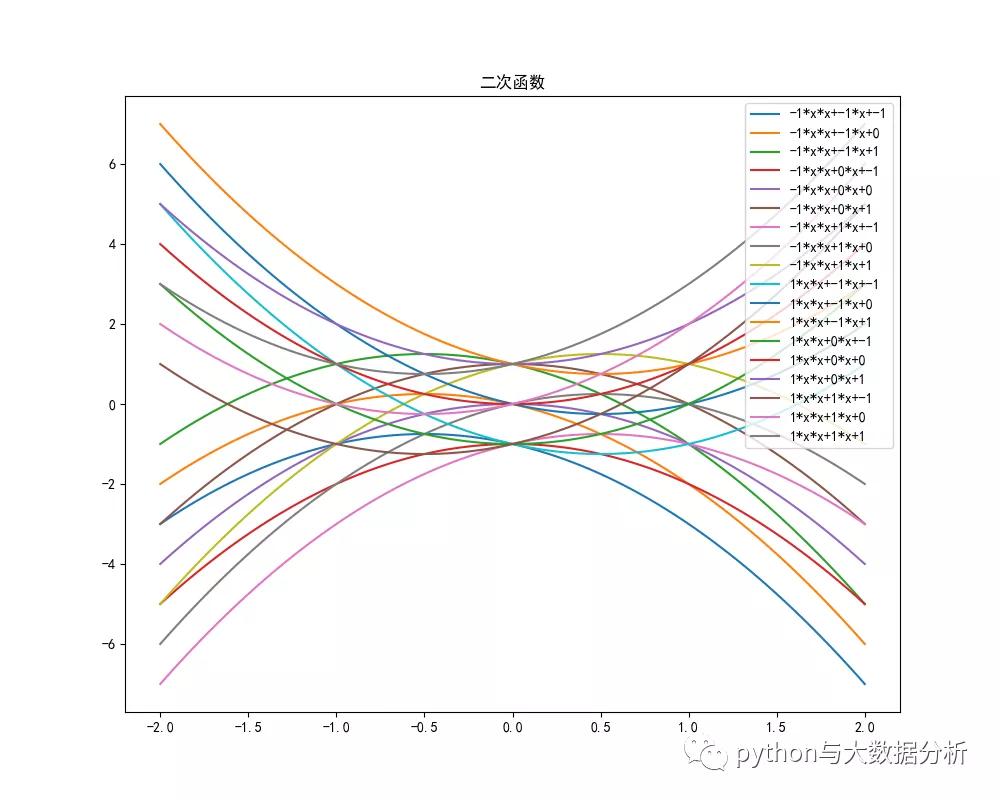
二次函數代碼如下：

  1. # 二次函數（quadratic function）的基本表示形式為y=ax²+bx+c（a≠0）。 
  2. # 二次函數最高次必須為二次， 二次函數的圖像是一條對稱軸與y軸平行或重合于y軸的拋物線。 
  3. # 其中a稱為二次項系數，b為一次項系數，c為常數項。x為自變量，y為因變量。等號右邊自變量的最高次數是2。 
  4. # 如果令y值等于零，則可得一個二次方程。該方程的解稱為方程的根或函數的零點。 
  5. # 頂點坐標 = (-b/2a,(4ac-b²)/4a 
  6. def Quadraticfunction(): 
  7.    fig = plt.figure(figsize=(10, 8)) 
  8.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  9.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  10.    x = np.linspace(-2, 2, 100) 
  11.  
  12.    alist = [-1, 1] 
  13.    blist = [-1, 0, 1] 
  14.    clist = [-1, 0, 1] 
  15.  
  16.    for a in alist: 
  17.       for b in blist: 
  18.          for c in clist: 
  19.             y = a * x * x + b * x + c 
  20.             label = '{}*x*x+{}*x+{}'.format(a, b, c) 
  21.             plt.plot(x, y, label=label) 
  22.    plt.title("二次函數") 
  23.    plt.legend() 
  24.    plt.show() 

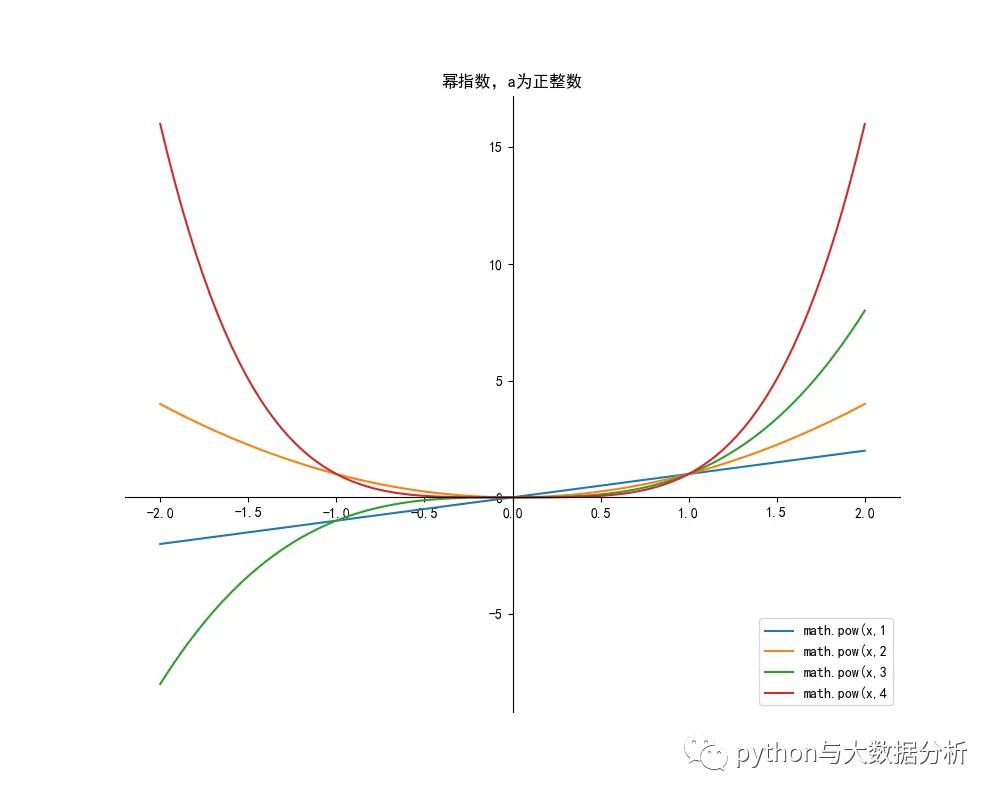
冪函數代碼如下：

  1. # 冪函數是基本初等函數之一。 
  2. # 一般地，y=xα（α為有理數）的函數，即以底數為自變量，冪為因變量，指數為常數的函數稱為冪函數。 
  3. # 例如函數y=x0 、y=x、y=x²、y=x³。 
  4. # a = 正數 
  5. # a 為>0 的自然數  x定義域(-∞,∞) 
  6. # a 為<0 的整數     X定義域(-∞,0),(0,∞) 
  7. # 
  8. # a >0 的分數 
  9. # a=n/m m為奇數，n為偶數，x定義域(-∞,∞)，y定義域[0,+∞） 
  10. # a=n/m m為奇數，n為奇數，x定義域(-∞,∞)，y定義域(-∞,∞) 
  11. # a=n/m m為偶數，n不限，x定義域[0,∞)，y定義域[0,+∞） 
  12. # 
  13. # a <0 的分數 
  14. # a=n/m m為奇數，n為偶數，x定義域(-∞,0),(0,∞)，y定義域(0,+∞） 
  15. # a=n/m m為奇數，n為奇數，x定義域(-∞,0),(0,∞)，y定義域(-∞,0),(0,∞) 
  16. # a=n/m m為偶數，n不限，x定義域(0,∞)，y定義域(0,+∞） 
  17. def powerfunction(): 
  18.    plt.figure(figsize=(10, 8)) 
  19.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  20.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  21.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  22.    x = np.linspace(-2, 2, 100) 
  23.    alist = [1, 2, 3, 4] 
  24.    for a in alist: 
  25.       y = np.power(x, a) 
  26.       label = 'math.pow(x,{}'.format(a) 
  27.       plt.plot(x, y, label=label) 
  28.  
  29.    # 設置圖片的右邊框和上邊框為不顯示 
  30.    ax.spines['right'].set_color('none') 
  31.    ax.spines['top'].set_color('none') 
  32.  
  33.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  34.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  35.    ax.spines['bottom'].set_position(('data', 0)) 
  36.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  37.    # ax.spines['left'].set_position(('axes', 0.5)) 
  38.    ax.spines['left'].set_position(('data', 0)) 
  39.    plt.title("冪指數，a為正整數") 
  40.    plt.legend() 
  41.    plt.show() 
  42.  
  43.    plt.figure(figsize=(10, 8)) 
  44.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  45.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  46.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  47.    x = np.append(np.linspace(-1, -0.01, 100), np.linspace(0.01, 1, 100)) 
  48.    alist = [-1, -2, -3] 
  49.    for a in alist: 
  50.       y = np.power(x, a) 
  51.       label = 'math.pow(x,{}'.format(a) 
  52.       plt.plot(x, y, label=label) 
  53.  
  54.    # 設置圖片的右邊框和上邊框為不顯示 
  55.    ax.spines['right'].set_color('none') 
  56.    ax.spines['top'].set_color('none') 
  57.  
  58.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  59.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  60.    ax.spines['bottom'].set_position(('data', 0)) 
  61.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  62.    # ax.spines['left'].set_position(('axes', 0.5)) 
  63.    ax.spines['left'].set_position(('data', 0)) 
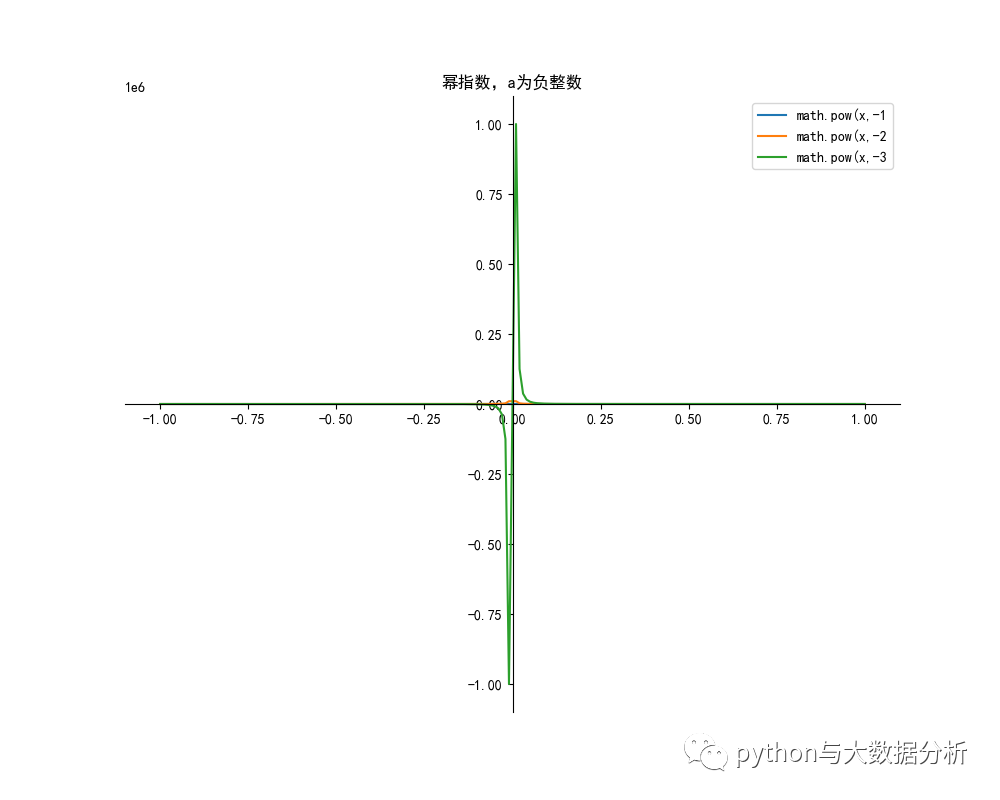
  64.    plt.title("冪指數，a為負整數") 
  65.    plt.legend() 
  66.    plt.show() 
  67.  
  68.    # a >0 的分數 
  69.    # a=n/m m為奇數，n為奇數，x定義域(-∞,∞)，y定義域(-∞,∞) 4/3 
  70.    # a=n/m m為奇數，n為偶數，x定義域[0,+∞)，y定義域[0,+∞）4/3 
  71.    # a=n/m m為偶數，n不限，x定義域(-∞,∞)，y定義域[0,+∞） 1/2,3/2 
  72.    plt.figure(figsize=(10, 8)) 
  73.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  74.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  75.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  76.    x = np.linspace(-2, 2, 100) 
  77.    alist = [1 / 3, 5 / 3, 7 / 3] 
  78.    for a in alist: 
  79.       # y = np.power(x, a) 
  80.       # RuntimeWarning: invalid value encountered in power 
  81.       y = np.float_power(abs(x), a) * np.sign(x) 
  82.       label = 'math.pow(x,{}'.format(a) 
  83.       plt.plot(x, y, label=label) 
  84.  
  85.    # 設置圖片的右邊框和上邊框為不顯示 
  86.    ax.spines['right'].set_color('none') 
  87.    ax.spines['top'].set_color('none') 
  88.  
  89.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  90.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  91.    ax.spines['bottom'].set_position(('data', 0)) 
  92.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  93.    # ax.spines['left'].set_position(('axes', 0.5)) 
  94.    ax.spines['left'].set_position(('data', 0)) 
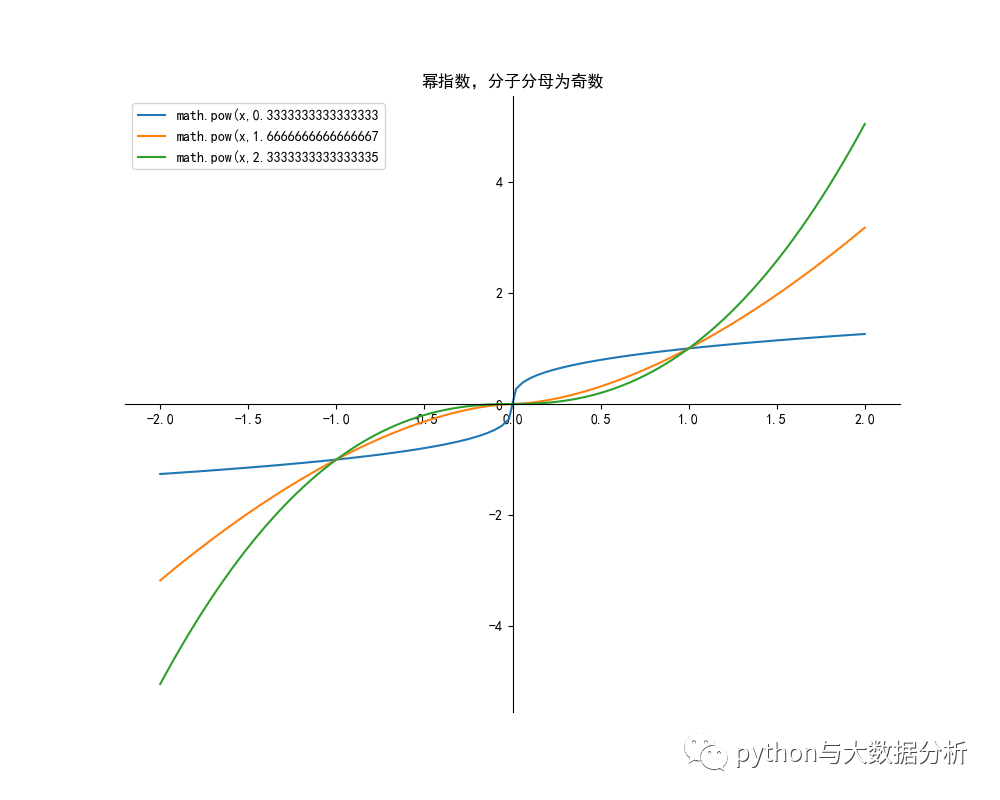
  95.    plt.title("冪指數，分子分母為奇數") 
  96.    plt.legend() 
  97.    plt.show() 
  98.  
  99.    plt.figure(figsize=(10, 8)) 
  100.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  101.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  102.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  103.    x = np.linspace(0, 2, 100) 
  104.    alist = [1 / 8, 1 / 4, 1 / 2] 
  105.    for a in alist: 
  106.       y = np.power(x, a) 
  107.       # y = np.float_power(abs(x), a) * np.sign(x) 
  108.       label = 'math.pow(x,{}'.format(a) 
  109.       plt.plot(x, y, label=label) 
  110.  
  111.    # 設置圖片的右邊框和上邊框為不顯示 
  112.    ax.spines['right'].set_color('none') 
  113.    ax.spines['top'].set_color('none') 
  114.  
  115.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  116.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  117.    ax.spines['bottom'].set_position(('data', 0)) 
  118.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  119.    # ax.spines['left'].set_position(('axes', 0.5)) 
  120.    ax.spines['left'].set_position(('data', 0)) 
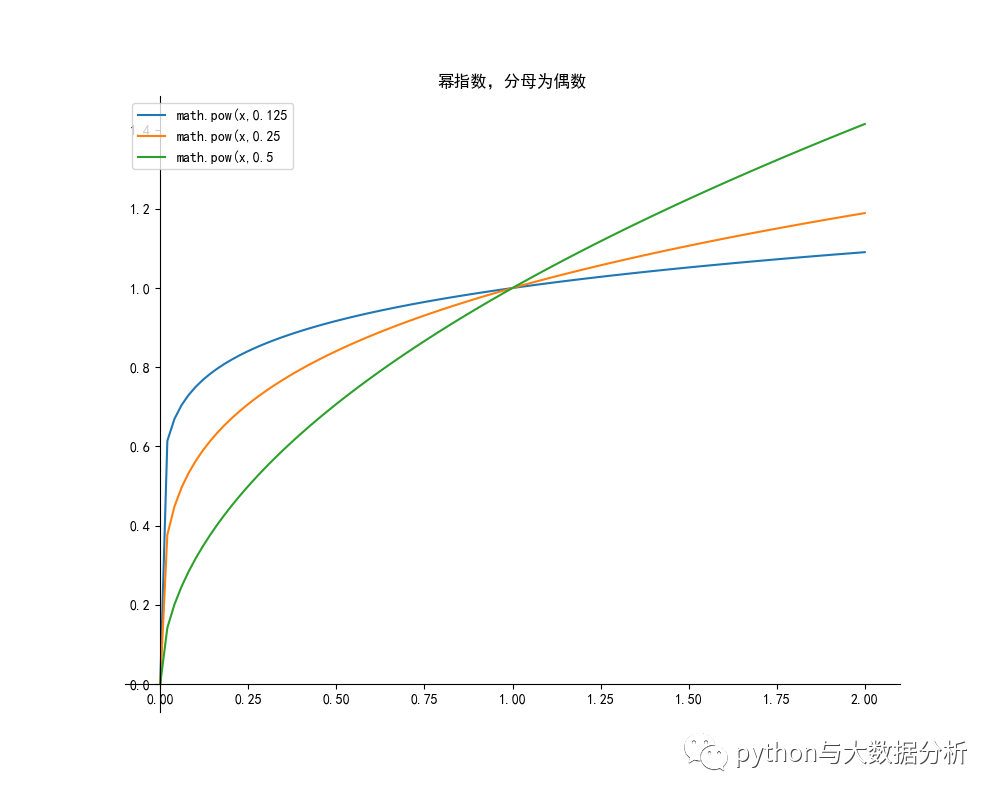
  121.    plt.title("冪指數，分母為偶數") 
  122.    plt.legend() 
  123.    plt.show() 
  124.  
  125.    plt.figure(figsize=(10, 8)) 
  126.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  127.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  128.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  129.    x = np.linspace(-2, 2, 100) 
  130.    alist = [2 / 3, 4 / 5, 6 / 7, 4 / 3, 8 / 5] 
  131.    for a in alist: 
  132.       y = np.power(abs(x), a) 
  133.       label = 'math.pow(x,{}'.format(a) 
  134.       plt.plot(x, y, label=label) 
  135.  
  136.    # 設置圖片的右邊框和上邊框為不顯示 
  137.    ax.spines['right'].set_color('none') 
  138.    ax.spines['top'].set_color('none') 
  139.  
  140.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  141.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  142.    ax.spines['bottom'].set_position(('data', 0)) 
  143.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  144.    # ax.spines['left'].set_position(('axes', 0.5)) 
  145.    ax.spines['left'].set_position(('data', 0)) 
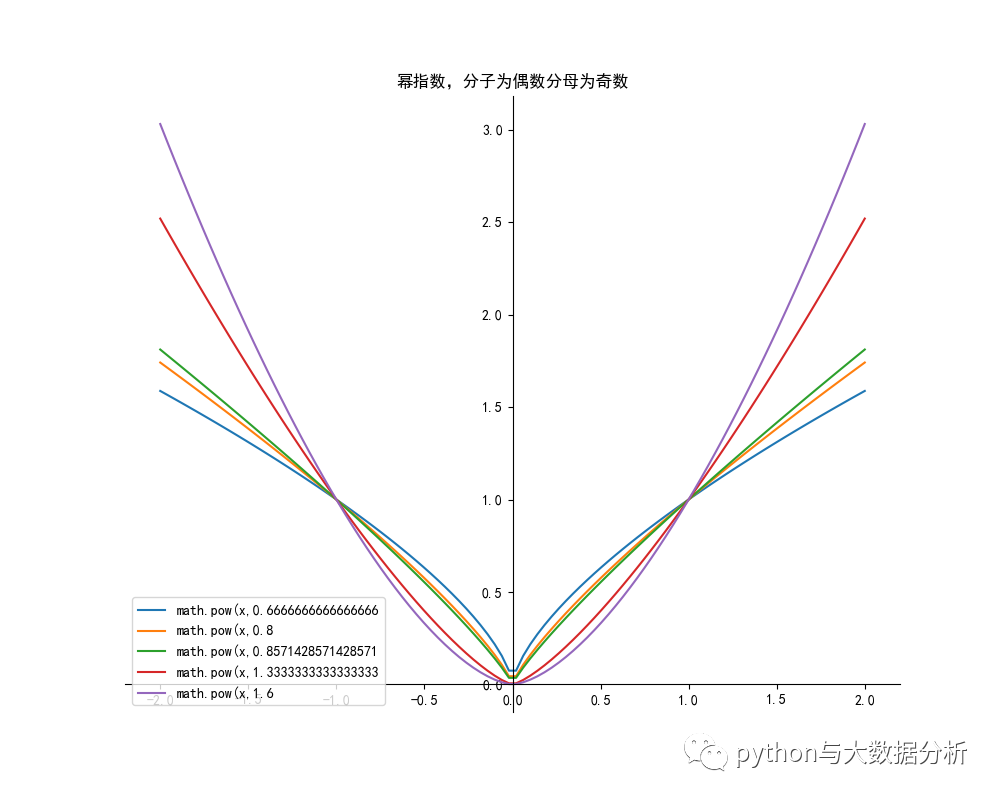
  146.    plt.title("冪指數，分子為偶數分母為奇數") 
  147.    plt.legend() 
  148.    plt.show() 
  149.  
  150.  
  151. # 關于負數就不再重復敘述了 
  152. # a <0 的分數 
  153. # a=n/m m為奇數，x定義域(-∞,0),(0,∞)，y定義域(0,+∞） 
  154. # a=n/m m為偶數，x定義域(-∞,0),(0,∞)，y定義域(-∞,0),(0,∞) 
  155. # a=n/m m為偶數，n為不限，x定義域(0,∞)，y定義域(0,+∞） 

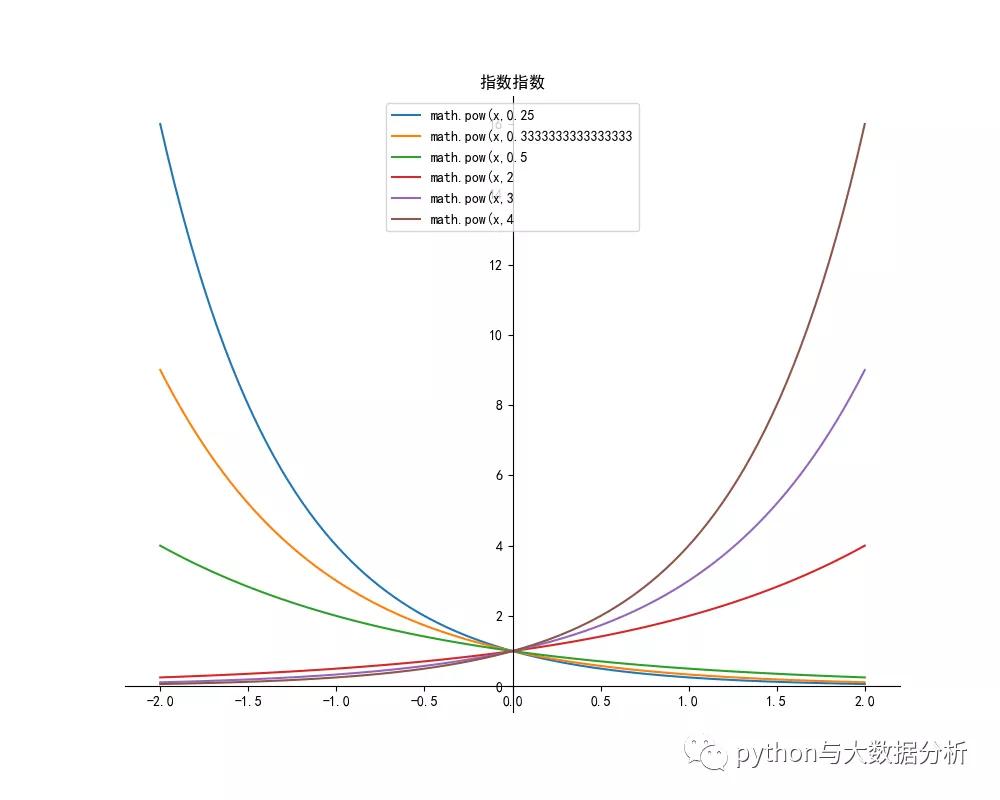
指數函數代碼如下：

  1. # 指數函數是重要的基本初等函數之一。 
  2.  
  3. # 一般地，y=ax函數(a為常數且以a>0，a≠1)叫做指數函數，函數的定義域是 R 。 [1] 
  4. # 注意，在指數函數的定義表達式中，在ax前的系數必須是數1，自變量x必須在指數的位置上，且不能是x的其他表達式， 
  5. # 否則，就不是指數函數 
  6. def exponentialfunction(): 
  7.    plt.figure(figsize=(10, 8)) 
  8.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  9.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  10.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  11.    # a>0 a!=1 
  12.    # 定義域為((-∞,∞)，值域為(0, +∞)，都通過(0, 1)點 
  13.    x = np.linspace(-2, 2, 100) 
  14.    alist = [1 / 4, 1 / 3, 1 / 2, 2, 3, 4] 
  15.    for a in alist: 
  16.       y = np.power(a, x) 
  17.       label = 'math.pow(x,{}'.format(a) 
  18.       plt.plot(x, y, label=label) 
  19.  
  20.    # 設置圖片的右邊框和上邊框為不顯示 
  21.    ax.spines['right'].set_color('none') 
  22.    ax.spines['top'].set_color('none') 
  23.  
  24.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  25.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  26.    ax.spines['bottom'].set_position(('data', 0)) 
  27.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  28.    # ax.spines['left'].set_position(('axes', 0.5)) 
  29.    ax.spines['left'].set_position(('data', 0)) 
  30.    plt.title("指數指數") 
  31.    plt.legend() 
  32.    plt.show() 

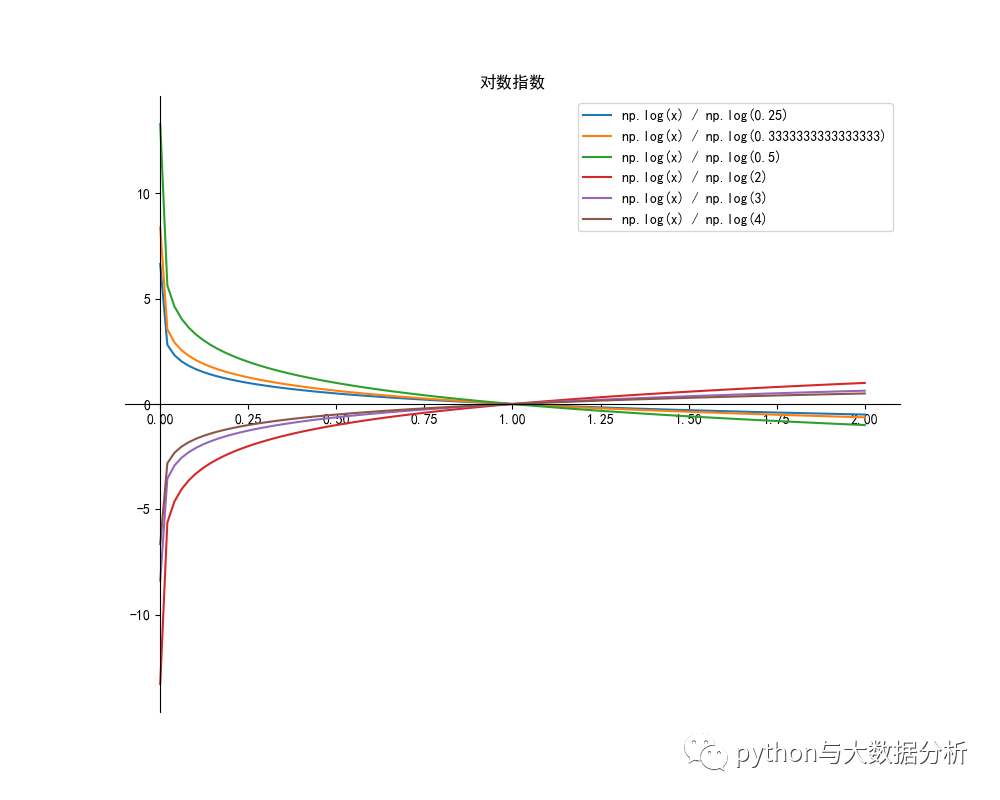
對數函數代碼如下：

  1. # 一般地，對數函數是以冪（真數）為自變量，指數為因變量，底數為常量的函數。 
  2. # 對數函數是6類基本初等函數之一。其中對數的定義： 
  3. # 如果ax =N（a>0，且a≠1），那么數x叫做以a為底N的對數，記作x=logaN，讀作以a為底N的對數，其中a叫做對數的底數，N叫做真數。 
  4. # 一般地，函數y=logaX（a>0，且a≠1）叫做對數函數，也就是說以冪（真數）為自變量，指數為因變量，底數為常量的函數，叫對數函數。 
  5. # 其中x是自變量，函數的定義域是（0，+∞），即x>0。它實際上就是指數函數的反函數，可表示為x=ay。因此指數函數里對于a的規定，同樣適用于對數函數。 
  6. def Logarithmicfunction(): 
  7.    plt.figure(figsize=(10, 8)) 
  8.    ax = plt.gca()  # 通過gca:get current axis得到當前軸 
  9.    plt.rcParams['font.sans-serif'] = ['SimHei']  # 繪圖中文 
  10.    plt.rcParams['axes.unicode_minus'] = False  # 繪圖負號 
  11.    # a>0 a!=1 
  12.    # 定義域為((-∞,∞)，值域為(0, +∞)，都通過(0, 1)點 
  13.    # 當a>1時，單調遞增 
  14.    # 當0<a<1時，單調遞減 
  15.    x = np.linspace(0.0001, 2, 100) 
  16.    alist = [1 / 4, 1 / 3, 1 / 2, 2, 3, 4] 
  17.    for a in alist: 
  18.       y = np.log(x) / np.log(a) 
  19.       label = 'np.log(x) / np.log({})'.format(a) 
  20.       plt.plot(x, y, label=label) 
  21.  
  22.    # 設置圖片的右邊框和上邊框為不顯示 
  23.    ax.spines['right'].set_color('none') 
  24.    ax.spines['top'].set_color('none') 
  25.  
  26.    # 挪動x，y軸的位置，也就是圖片下邊框和左邊框的位置 
  27.    # data表示通過值來設置x軸的位置，將x軸綁定在y=0的位置 
  28.    ax.spines['bottom'].set_position(('data', 0)) 
  29.    # axes表示以百分比的形式設置軸的位置，即將y軸綁定在x軸50%的位置 
  30.    # ax.spines['left'].set_position(('axes', 0.5)) 
  31.    ax.spines['left'].set_position(('data', 0)) 
  32.    plt.title("對數指數") 
  33.    plt.legend() 
  34.    plt.show() 

 

責任編輯：武曉燕 來源： python與大數據分析
python初等函數
相關推薦

2021-07-30 05:00:04

Python初等函數

2021-07-30 06:58:27

python實現三角函數

2021-08-11 07:02:04

Python激活函數

2016-11-14 15:16:42

Android

2020-06-05 14:29:07

PythonPandas數據分析

2021-08-31 20:21:11

VitessMySQL分庫

2021-03-31 07:39:18

pythonHIVEUDF函數

2011-07-18 14:54:55

HTML 5

2018-04-08 07:49:05

應用集成EAI應用系統

2016-10-20 21:02:12

微信小程序javascript

2023-02-28 08:24:49

2011-12-26 16:39:43

局部函數

2013-03-04 09:47:08

Python函數式編程

2023-09-11 06:12:31

盒子模型CSS

2024-04-29 14:58:48

Python內置函數

2012-01-12 09:32:17

響應式Web設計

2014-11-12 13:26:55

創業

2021-08-30 08:23:34

Go語言進程

2021-10-08 08:58:35

MySQL函數脫敏

2023-11-23 19:30:35

Python編程語言
點贊
收藏

51CTO技術棧公眾號

主站蜘蛛池模板： 久久国产精品久久久久久久久久 | 国产乱码精品1区2区3区 | www.日韩在线 | 国产免费a视频 | 亚洲一区二区电影网 | 色综合美女 | 精品真实国产乱文在线 | a中文在线视频 | a级在线免费观看 | 久久成人在线视频 | 91极品欧美视频 | 久久久免费精品 | 五月综合激情网 | 亚洲一区二区在线播放 | 欧美精品一区二区三区四区五区 | 91视频久久 | 国产精品美女久久久 | 亚洲视频在线免费观看 | av一区二区三区四区 | 中文字幕三区 | 91文字幕巨乱亚洲香蕉 | 成人免费精品视频 | 成人在线免费观看视频 | 久久久久国产一区二区三区四区 | 天久久| 日本精品视频 | 日韩精品一区二区三区在线播放 | 成人免费大片黄在线播放 | 欧美一区二区在线观看 | 欧美在线免费 | 免费a国产 | 日韩另类 | 国产精品成人一区二区三区 | 黄色一级特级片 | 99re热这里只有精品视频 | 亚洲成av人片在线观看 | 成人影院在线观看 | 国产一区二区三区免费视频 | 黄色一级大片视频 | 午夜免费视频 | 国产精品一区二区福利视频 |