現(xiàn)代 AI 系統(tǒng)可以像勤奮的學(xué)生準(zhǔn)備考試一樣，去處理諸如識別圖像中的對象以及預(yù)測蛋白質(zhì) 3D 結(jié)構(gòu)之類的任務(wù)。通過大量示例問題訓(xùn)練，這類系統(tǒng)可以逐漸降低錯誤，直至取得成功。

但這是一項需要獨自完成的工作，并且只是已知的學(xué)習(xí)形式之一。學(xué)習(xí)也需要與他人互動和交流。一個單獨的個體很難自行解決極其復(fù)雜的問題。通過讓問題解決方案具有類游戲的特質(zhì)，DeepMind 之前在研究中已經(jīng)訓(xùn)練了 AI 智能體 (Agent) 來玩奪旗賽并在《星際爭霸》中達(dá)到大師級水平。因此，我們希望了解基于，以博弈論為模型的視角能否幫助解決其他基本的機(jī)器學(xué)習(xí)問題。

[[419288]]

最近，在 2021 年 ICLR 上，我們發(fā)表了論文 “EigenGame：將 PCA 作為納什均衡 (EigenGame: PCA as a Nash Equilibrium)”，并獲得杰出論文獎。我們的研究探索了一種解決舊問題的新方法：我們將主成分分析 (PCA)(一種特征值問題)重新表述為競爭性的多智能體博弈游戲，即 EigenGame。PCA 通常表現(xiàn)為優(yōu)化問題(或單智能體問題);但是，我們發(fā)現(xiàn)多智能體視角可使我們利用最新的計算資源生成新的數(shù)據(jù)分析和算法。這使得我們能夠?qū)⒅鞒煞址治鰯U(kuò)展到以往計算密集型的大規(guī)模數(shù)據(jù)集，并為未來的研究探索提供一種替代方法。

將 PCA 作為納什均衡

PCA (Principal component analysis) 最早于 20 世紀(jì)初期提出，之后便成為了分析高維數(shù)據(jù)結(jié)構(gòu)長期使用的一項技術(shù)。現(xiàn)在，這種方法已普遍用作數(shù)據(jù)處理流水線中的第一步，簡化了集群和可視化數(shù)據(jù)。同時，它也是學(xué)習(xí)低維表示以進(jìn)行回歸和分類的實用工具。自 PCA 提出后的一個多世紀(jì)，我們?nèi)匀挥谐浞值睦碛蓪ζ溥M(jìn)行學(xué)習(xí)和研究。

首先，數(shù)據(jù)最初是由人工用紙筆記錄，而現(xiàn)在則存儲在像倉庫一樣大的數(shù)據(jù)中心。結(jié)果，這種熟悉的分析方式成為了計算瓶頸。研究人員已經(jīng)探索了隨機(jī)算法和其他方向來改善 PCA 的擴(kuò)展方式，但是我們發(fā)現(xiàn)，這些方法難以擴(kuò)展到大規(guī)模數(shù)據(jù)集，因為它們無法完全利用計算領(lǐng)域以深度學(xué)習(xí)為中心的最新進(jìn)展：即訪問多個并行 GPU 或 TPU。

其次，PCA 與許多重要的機(jī)器學(xué)習(xí)和工程問題都需要使用共同的解決方案，即奇異值分解 (SVD)。通過以正確的方式解決 PCA 問題，我們的數(shù)據(jù)分析和算法將更廣泛地應(yīng)用于機(jī)器學(xué)習(xí)樹的各個分支。 

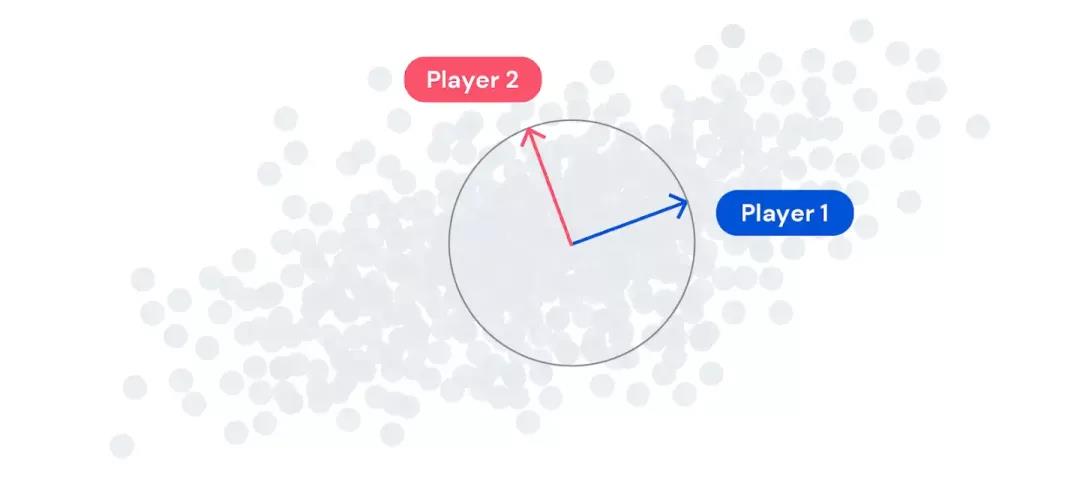
與任何棋盤游戲一樣，為了將 PCA 重新設(shè)計為游戲，我們需要制定一套規(guī)則和目標(biāo)讓玩家遵循。設(shè)計此類游戲的方式有很多種;但是，重要的設(shè)計理念源自 PCA 本身：最佳解決方案由特征向量組成，而特征向量捕獲數(shù)據(jù)中的重要方差并且彼此正交。 

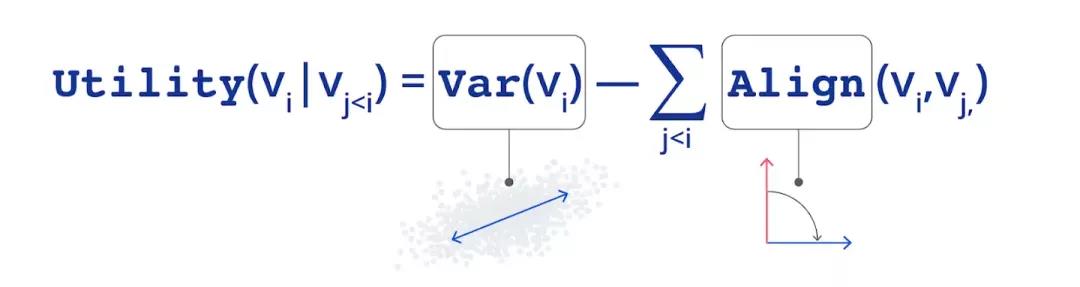
在 EigenGame 中，每個玩家都控制一個特征向量。玩家通過解釋數(shù)據(jù)中的方差來提高得分，但如果他們與其他玩家過于相似，則會受到懲罰。我們還建立了一個層次結(jié)構(gòu)：玩家 1 只關(guān)注最大化方差，而其他玩家則還必須關(guān)注如何最小化與層級結(jié)構(gòu)中高于自己的玩家的相似度。這種獎勵和懲罰的組合決定了每個玩家的效用。 

通過經(jīng)適當(dāng)設(shè)計的方差 Var 和對齊 Align 項，我們證明了：

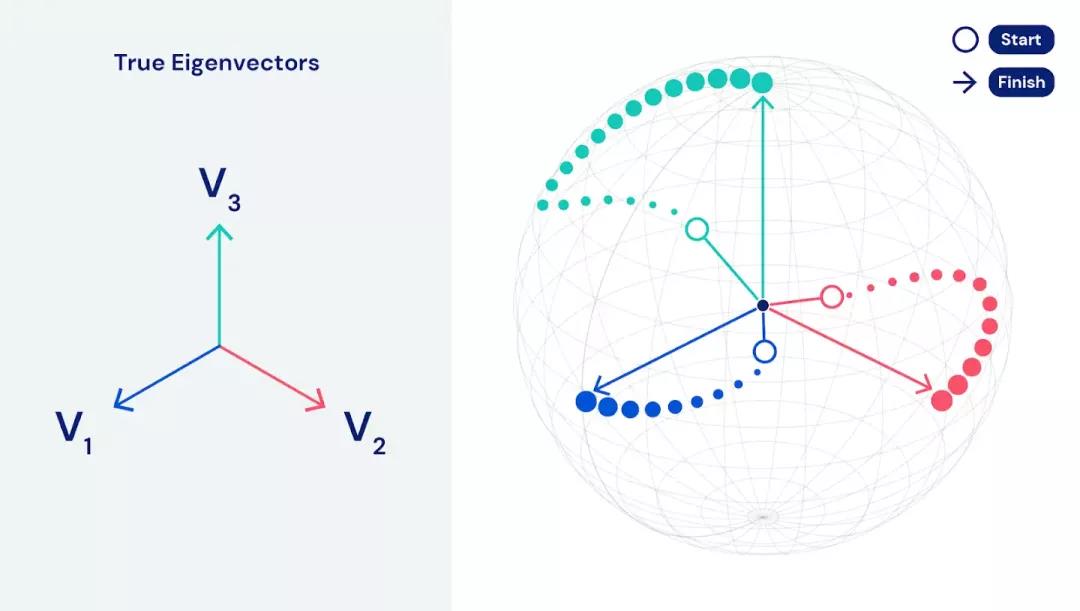
• 如果所有的玩家都表現(xiàn)最優(yōu)，他們則一起實現(xiàn)了游戲的納什均衡點，而這就是 PCA 算法的解決方案。
• 如果每個玩家單獨且同步使用梯度上升法來最大化其效用，則可實現(xiàn)該目標(biāo)。

這種同步上升的獨立性特別重要，因為它允許將計算分布在數(shù)十個 Google Cloud TPU 上，從而實現(xiàn)數(shù)據(jù)和模型并行。這使我們的算法適應(yīng)真正的大規(guī)模數(shù)據(jù)成為了可能。EigenGame 可以在數(shù)小時內(nèi)找到包含數(shù)百萬個特征或數(shù)十億行的上百兆字節(jié)數(shù)據(jù)集的主要成分。 

效用、更新及兩者之間的一切

通過從多智能體角度審視 PCA，我們能夠提出可擴(kuò)展的算法和新穎的分析方法。我們還發(fā)現(xiàn)了與赫布學(xué)習(xí) (Hebbian Learning) 存在的驚人聯(lián)系，或者也可以說神經(jīng)元在學(xué)習(xí)時如何調(diào)整適應(yīng)。在 EigenGame 中，每個最大化效用的玩家都會產(chǎn)生更新方程，該方程類似于從關(guān)于大腦中突觸可塑性的赫布模型中衍生的更新規(guī)則。我們已知赫布更新可以收斂到 PCA 解決方案，但不能作為任何效用函數(shù)的梯度導(dǎo)出。博弈論為我們提供了一個新的視角來研究赫布學(xué)習(xí)，也為機(jī)器學(xué)習(xí)問題提供了一系列的解決方法。

機(jī)器學(xué)習(xí)連續(xù)曲線的一端是提出可優(yōu)化的目標(biāo)函數(shù)的完善路徑：使用凸優(yōu)化和非凸優(yōu)化理論，研究人員可以對解決方案的整體性質(zhì)進(jìn)行推理。而在另一端上，則直接指定了受神經(jīng)科學(xué)啟發(fā)的純聯(lián)結(jié)主義方法和更新規(guī)則，但是這可能增加了對整個系統(tǒng)的分析難度，常常需要研究復(fù)雜的動力系統(tǒng)。

像 EigenGame 這樣的游戲理論方法則介于兩者之間。玩家更新將不受限于函數(shù)的梯度，而只是對其他玩家當(dāng)前策略的最佳響應(yīng)。我們可以自由設(shè)計具有必要屬性的效用函數(shù)程序和更新，例如，指定無偏或加速的更新，同時確保納什屬性仍然允許我們對整個系統(tǒng)進(jìn)行分析。 

EigenGame 形象地展示了如何將機(jī)器學(xué)習(xí)問題的解決方案設(shè)計為大型多智能體系統(tǒng)的輸出。一般而言，將機(jī)器學(xué)習(xí)問題設(shè)計為多智能體游戲是頗具挑戰(zhàn)性的機(jī)制設(shè)計問題;但是，研究人員已經(jīng)使用兩個玩家間的這類零和博弈來解決機(jī)器學(xué)習(xí)問題。最值得注意的是，生成對抗網(wǎng)絡(luò) (GAN) 這一生成建模方法的成功吸引了人們對博弈論與機(jī)器學(xué)習(xí)之間關(guān)系的興趣。

EigenGame 超越了這一點，進(jìn)入了更為復(fù)雜的多玩家非零和博弈設(shè)置。這優(yōu)化了并行性，從而能夠支持更大的規(guī)模和速度。它還為機(jī)器學(xué)習(xí)的相關(guān)社區(qū)提供了可量化的基準(zhǔn)，以測試新穎的多智能體算法以及更豐富的領(lǐng)域，例如外交風(fēng)云和足球。

我們希望我們的效用和更新設(shè)計藍(lán)圖能夠鼓勵其他人探索設(shè)計算法、智能體和系統(tǒng)的新方向。我們期待未來能看到其他問題也可表述為游戲，以及我們收集的數(shù)據(jù)分析是否會進(jìn)一步增進(jìn)我們對多智能體的智能本質(zhì)的理解。