GNN入門必看!Google Research教你從毛坯開始搭建sota 圖神經網絡
近幾年,神經網絡在自然語言、圖像、語音等數據上都取得了顯著的突破,將模型性能帶到了一個前所未有的高度,但如何在圖數據上訓練仍然是一個可研究的點。
傳統神經網絡輸入的數據通常每個sample之間都不存在關系,而圖數據更加復雜,每個節點之間存在聯系,也更符合真實世界中的數據存儲方式。真實世界的物體通常根據它們與其他事物的聯系來定義的,一組對象以及它們之間的聯系可以很自然地表示為一個圖(graph),基于圖數據的神經網絡也稱為Graph Neural Network(GNN)。
圖神經網絡的發展逐漸受到更多關注,在推理、常識等方面也取得很多成就,來自Google的研究員們最近發表了一篇博客,介紹了圖神經網絡的發展歷程,還對現代圖神經網絡進行了探討和解釋。
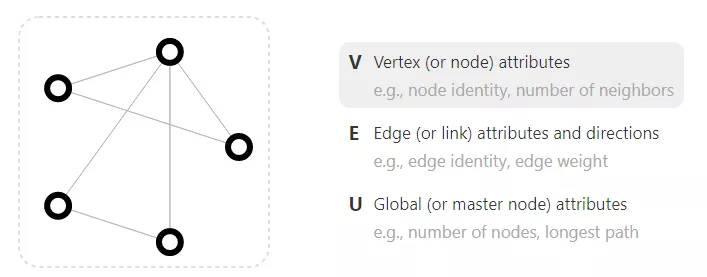
一個圖由頂點和邊組成,在人的腦海中,可以很自然地把社交網絡等數據表示為圖,那如何把圖像和文本表示為圖你想過嗎?
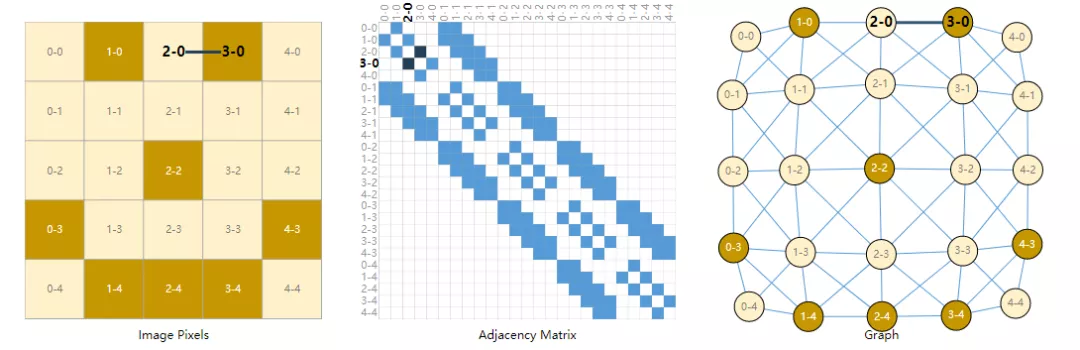
通常認為圖像是帶有通道(channels)的矩形網格,將它們表示為例如244x244x3的三維矩陣。
另一種看待圖像的方式是有規則結構的圖像,其中每個像素代表一個節點,并通過邊緣連接到相鄰的像素。每個非邊界像素恰好有8個相鄰節點,并且存儲在每個節點上的信息是表示像素 RGB 值的三維向量。
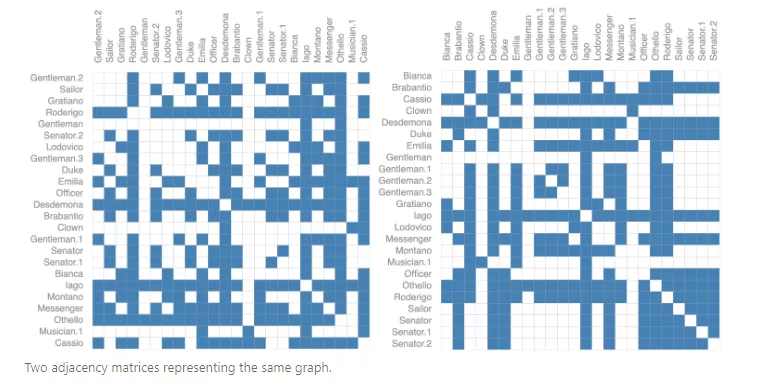
可視化圖的連通性的一種方法是鄰接矩陣。對這些節點進行排序,在一個5x5的圖像中有25個像素,構造一個矩陣,如果兩個節點之間存在一條邊那么在鄰接矩陣中就存在一個入口。
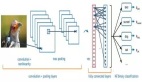
對于文本來說,可以將索引與每個字符、單詞或標記相關聯,并將文表示為一個有向圖,其中每個字符或索引都是一個節點,并通過一條邊連接到后面的節點。
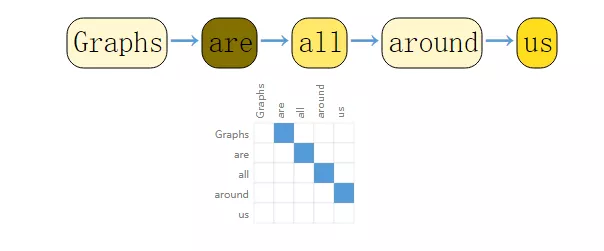
但文本和圖像在實際使用上通常不采用這種編碼方式,用圖來表示是比較多余的一步操作,因為所有圖像和文本都具有非常規則的結構。例如,圖像的鄰接矩陣中通常有一條帶狀結構,因為所有的節點或像素都連接包含在在一個網格結構中。文本的鄰接矩陣只包括一條對角線,因為每個單詞只連接到前一個單詞和下一個單詞。
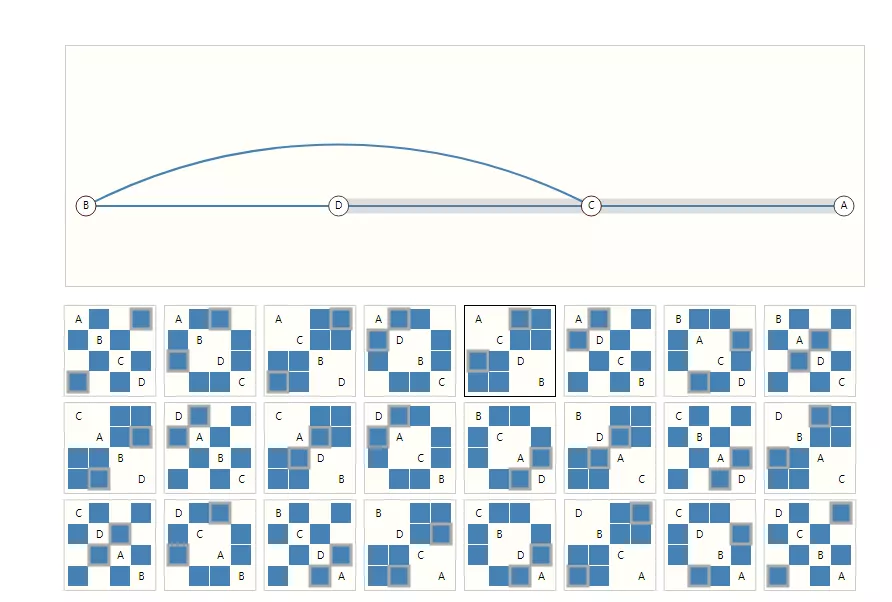
在使用神經網絡表示圖任務時,一個最重要的表示就是它的連通性,一個比較好的選擇就是鄰接矩陣,但如前文所說,鄰接矩陣過于稀疏,空間利用率不高;另一個問題就是同一個圖的鄰接矩陣有多種表示方法,神經網絡無法保證這些鄰接矩陣的輸出結果都相同,也就是說不存在置換不變性(permutation invariant)。
并且不同形狀的圖可能也包含相同的鄰接矩陣。
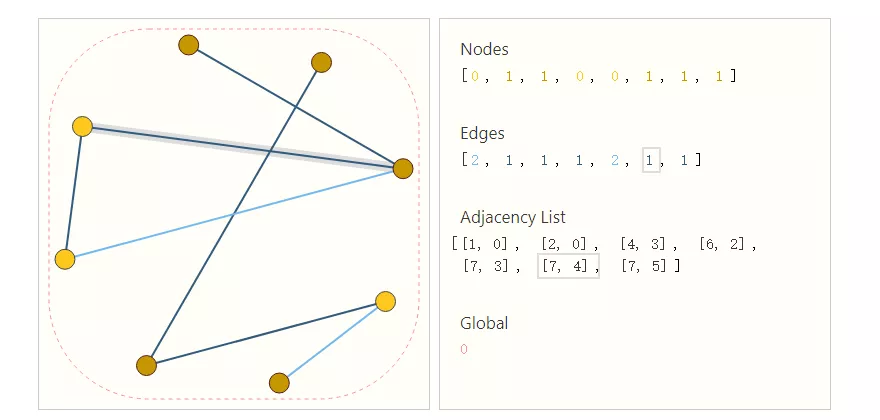
一種優雅且高效來表示稀疏矩陣的方法是鄰接列表。它們將節點之間的邊的連通性描述為鄰接列表第k個條目中的元組(i,j)。由于邊的數量遠低于鄰接矩陣的條目數量,因此可以避免了在圖的斷開部分(不含邊)進行計算和存儲。
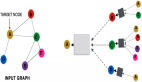
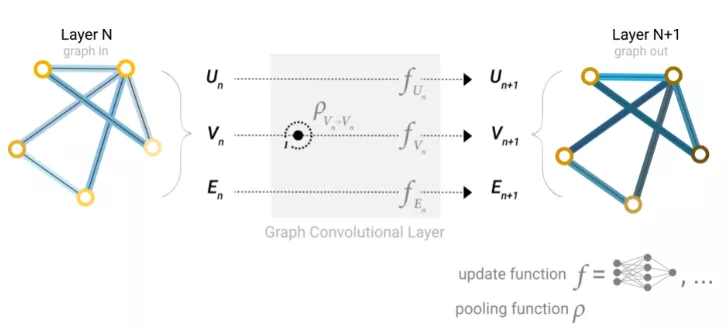
既然圖的描述是以排列不變的矩陣格式,那圖神經網絡(GNNs)就可以用來解決圖預測任務。GNN是對圖的所有屬性(節點、邊、全局上下文)的可優化變換,它可以保持圖的對稱性(置換不變性)。GNN采用“圖形輸入,圖形輸出”架構,這意味著這些模型類型接受圖作為輸入,將信息加載到其節點、邊和全局上下文,并逐步轉換這些embedding,而不更改輸入圖形的連通性。
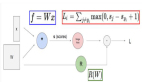
最簡單的GNN模型架構還沒有使用圖形的連通性,在圖的每個組件上使用一個單獨的多層感知器(MLP)(其他可微模型都可以)就可以稱之為GNN層。
對于每個節點向量,使用MLP并返回一個可學習的節點向量。對每一條邊也做同樣的事情,學習每一條邊的embedding,也對全局上下文向量做同樣的事情,學習整個圖的單個embedding。
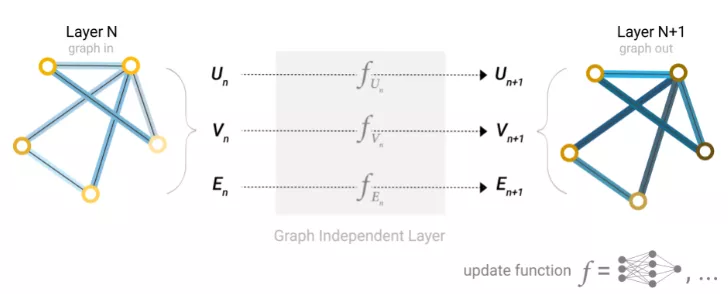
與神經網絡模塊或層一樣,我們可以將這些GNN層堆疊在一起。
由于GNN不會更新輸入圖的連通性,因此可以使用與輸入圖相同的鄰接列表和相同數量的特征向量來描述GNN的輸出圖。
構建了一個簡單的GNN后,下一步就是考慮如何在上面描述的任務中進行預測。
首先考慮二分類的情況,這個框架也可以很容易地擴展到多分類或回歸情況。如果任務是在圖節點上進行二分類預測,并且圖已經包含節點信息,那么對于每個節點embedding應用線性分類器即可。
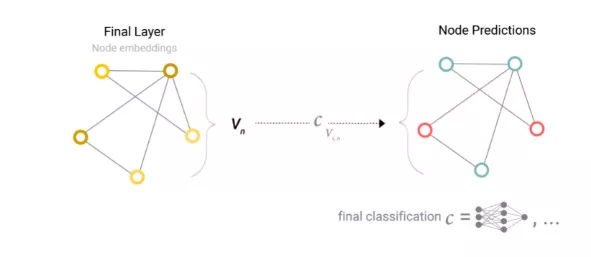
實際情況可能更復雜,例如圖形中的信息可能存儲在邊中,而且節點中沒有信息,但仍然需要對節點進行預測。所以就需要一種從邊收集信息并將其提供給節點進行預測的方法。
可以通過Pooling來實現這一點。Pooling分兩步進行:對于要池化的每個item,收集它們的每個embedding并將它們連接到一個矩陣中,通常通過求和操作聚合收集的embedding。
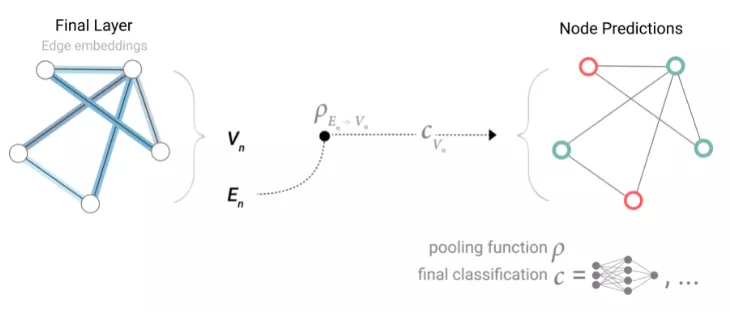
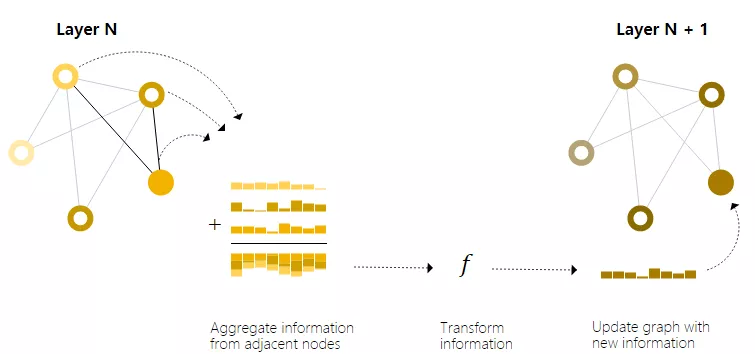
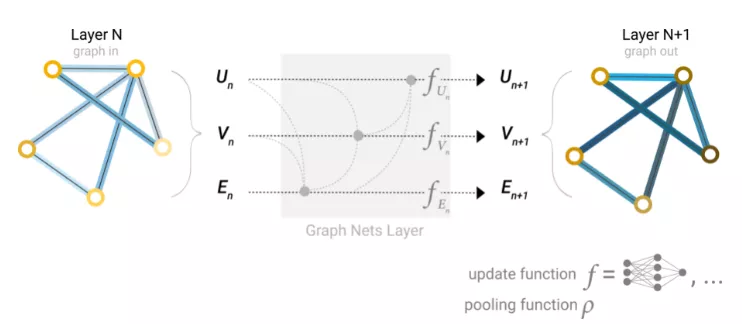
更復雜地,可以通過在 GNN 層內使用池化來進行更復雜的預測,以使學習到的embedding更了解圖的連通性。可以使用消息傳遞(Message Passing)來做到這一點,其中相鄰節點或邊緣交換信息并影響彼此更新的embedding。
消息傳遞包含三個步驟:
1、對于圖中的每個節點,收集所有相鄰節點embedding(或消息)。
2、通過聚合函數(如sum)聚合所有消息。
3、所有匯集的消息都通過一個更新函數傳遞,通常是一個學習的神經網絡。
這些步驟是利用圖的連接性的關鍵,還可以在GNN層中構建更復雜的消息傳遞變體,以產生更高表達能力的GNN模型。
本質上,消息傳遞和卷積是聚合和處理元素的鄰居信息以更新元素值的操作。在圖中,元素是節點,在圖像中,元素是像素。然而,圖中相鄰節點的數量可以是可變的,這與圖像中每個像素都有一定數量的相鄰元素不同。通過將傳遞給GNN層的消息堆疊在一起,節點最終可以合并整個圖形中的信息。
節點學習完embedding后的下一步就是邊。在真實場景中,數據集并不總是包含所有類型的信息(節點、邊緣和全局上下文),當用戶想要對節點進行預測,但提供的數據集只有邊信息時,在上面展示了如何使用池將信息從邊路由到節點,但也僅局限在模型的最后一步預測中。除此之外,還可以使用消息傳遞在GNN層內的節點和邊之間共享信息。
可以采用與之前使用相鄰節點信息相同的方式合并來自相鄰邊緣的信息,首先合并邊緣信息,使用更新函數對其進行轉換并存儲。
但存儲在圖中的節點和邊信息不一定具有相同的大小或形狀,因此目前還沒有一種明確有效的方法來組合他們,一種比較好的方法是學習從邊空間到節點空間的線性映射,反之亦然。或者,可以在update函數之前將它們concatenate在一起。
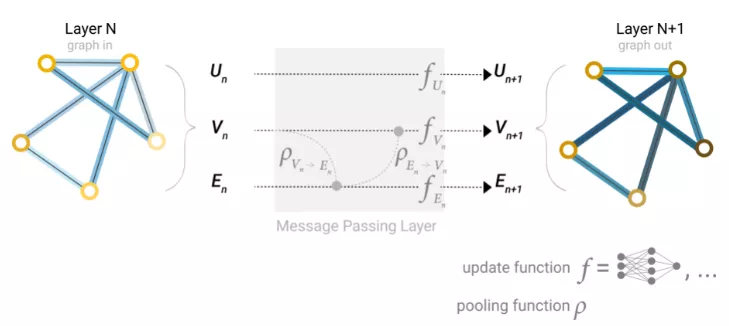
最后一步就是獲取全局的節點、邊表示。
之前所描述的網絡存在一個缺陷:即使多次應用消息傳遞,在圖中彼此不直接連接的節點可能永遠無法有效地將信息傳遞給彼此。對于一個節點,如果有k層網絡,那么信息最多傳播k步。
對于預測任務依賴于相距很遠的節點或節點組的情況,這可能是一個問題。一種解決方案是讓所有節點都能夠相互傳遞信息。但不幸的是,對于大型的圖來說,所需要的計算成本相當高,但在小圖形中已經可以有所應用。
這個問題的一個解決方案是使用圖(U)的全局表示,它有時被稱為主節點或上下文向量。該全局上下文向量連接到網絡中的所有其他節點和邊,并可以作為它們之間傳遞信息的橋梁,為整個圖形建立表示。這可以創建一個比其他方法更豐富、更復雜的圖形表示。
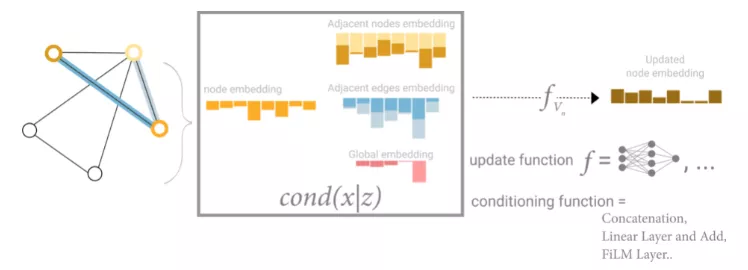
從這方面來看,所有的圖形的屬性都已經學習到了對應的表示,因此可以通過調整感興趣的屬性相對于其余屬性的信息在池中利用它們。例如對于一個節點,可以考慮來自相鄰節點、連接邊和全局信息的信息。為了將新節點嵌入到所有這些可能的信息源上,還可以簡單地將它們連接起來。此外,還可以通過線性映射將它們映射到同一空間,并應用特征調節層(feature-wise modulation layer)。
通過上述流程,相信大家已經對簡單的GNN如何發展為sota模型有了了解。在獲取圖的節點、邊表示后,就可以為之后的任務再單獨設計網絡,GNN為神經網絡提供了一種處理圖數據的方式。
在原文博客中,還包括一些GNN的真實案例和數據集,并了解GNN在其中的具體作用,想了解更多內容可以訪問參考鏈接進行閱讀。