集成多關(guān)系圖神經(jīng)網(wǎng)絡(luò)

作者：王玉玲 2023-05-04 07:39:14

本次分享是基于Datafun 圖學(xué)習(xí)峰會(huì)活動(dòng)整理，作者為北京郵電大學(xué)在讀博士王玉玲，相關(guān)成果為在美團(tuán)NLP中心大模型應(yīng)用組實(shí)習(xí)期間產(chǎn)出。

一、統(tǒng)一視角的 GNN

1、現(xiàn)有 GNN 傳播范式

空域的 GNN 是如何傳播的？如下圖所示，以節(jié)點(diǎn) A 為例:

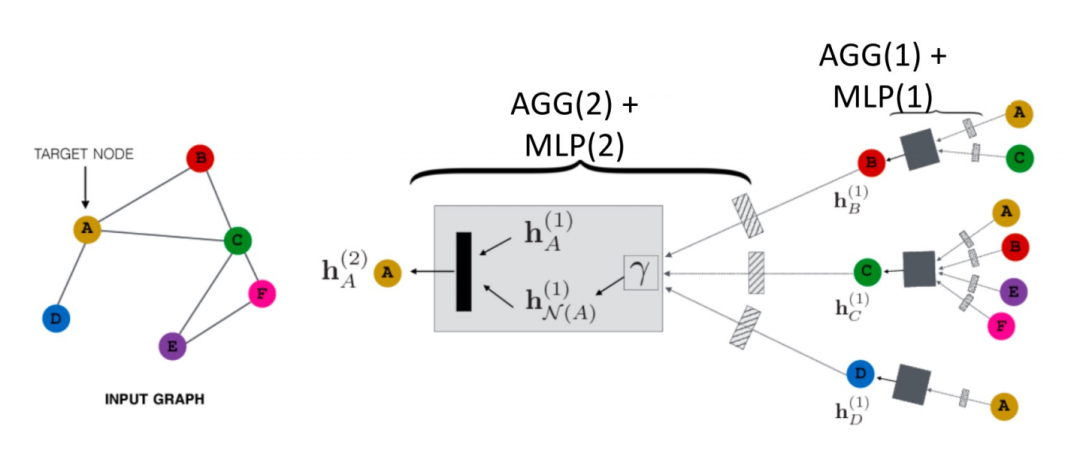
首先其會(huì)將其鄰居節(jié)點(diǎn) N (A) 的信息聚合成一個(gè) h_N(A)⁽¹⁾，再和 A 其上一層的表示 h_N(A)⁽¹⁾進(jìn)行組合，然后經(jīng)過(guò)一個(gè) transformation 函數(shù)（即公式中的Trans(·)），就得到了 A 的下一層表示 h_N(A)⁽²⁾。這個(gè)就是一個(gè)最基本的 GCN 的傳播范式。

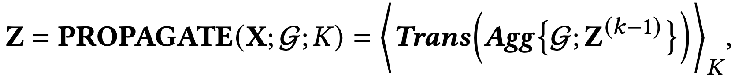
另外，還有一種解耦的傳播范式（decoupled propagation process）：

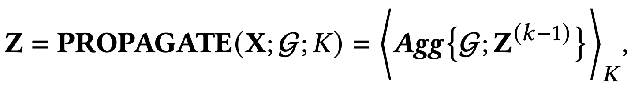
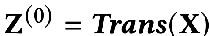
這兩種方式有什么區(qū)別呢？解耦的傳播范式中會(huì)先用一個(gè)特征提取器，也就是transformation 函數(shù)對(duì)初始的特征進(jìn)行提取，然后將提取后的特征再放入聚合函數(shù)中進(jìn)行聚合，可以看到這種方式將特征的提取與聚合分開(kāi)了，即做到了解耦。這樣做的好處在于：

可以自由的去設(shè)計(jì)前面的這個(gè) transformation 函數(shù)，可以用任何的模型。
在聚合時(shí)可以增加很多層，來(lái)獲得更遠(yuǎn)距離的連接信息，但是我們不會(huì)面臨過(guò)度參數(shù)化的風(fēng)險(xiǎn)，因?yàn)榫酆虾瘮?shù)中沒(méi)有需要優(yōu)化的參數(shù)。

上面就是兩種主要的范式，而節(jié)點(diǎn)的 embedding 輸出可以使用網(wǎng)絡(luò)的最后一層，也可以使用中間層的殘差。

通過(guò)上面的回顧我們可以看到 GNN 中有兩個(gè)基本的信息源：

網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)：一般可以捕捉圖結(jié)構(gòu)的同配信息屬性。
節(jié)點(diǎn)的特征：一般都會(huì)包含節(jié)點(diǎn)的低頻、高頻信號(hào)。

2、一個(gè)統(tǒng)一的優(yōu)化框架

基于 GNN 的傳播機(jī)制，我們可以發(fā)現(xiàn)，現(xiàn)有的 GNN 有兩個(gè)共同的目標(biāo)：

從節(jié)點(diǎn)的特征中去編碼有用的信息。
使用拓?fù)浣Y(jié)構(gòu)的平滑能力。

那么能否用數(shù)學(xué)語(yǔ)言去描述這兩個(gè)目標(biāo)呢？有人就提出了下面用公式表示的 GNN 優(yōu)化統(tǒng)一框架：

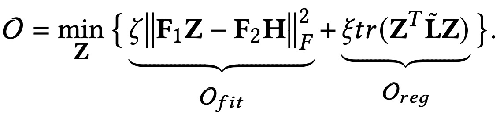
優(yōu)化目標(biāo)中的第一項(xiàng) ：

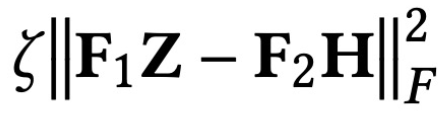
是特征擬合項(xiàng)，它的目標(biāo)是讓學(xué)習(xí)到的節(jié)點(diǎn)表示 Z 盡可能與原始特征 H 接近，而 F₁, F₂是可以自由設(shè)計(jì)的圖卷積核。當(dāng)卷積核為單位矩陣 I 時(shí)，就相當(dāng)于一個(gè)全通濾波器；當(dāng)卷積核為 0 矩陣時(shí)就是低通濾波器，當(dāng)卷積核為拉普拉斯矩陣 L 時(shí)就是高通濾波器。

優(yōu)化目標(biāo)的第二項(xiàng)形式上看是一個(gè)矩陣的跡，其作用是圖上的正則項(xiàng)，跡與正則有什么關(guān)系呢？其實(shí)第二項(xiàng)展開(kāi)后是下面這個(gè)形式：

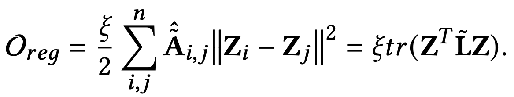
其含義是捕獲圖上任意兩個(gè)相鄰節(jié)點(diǎn)之間特征的差異程度，代表了一個(gè)圖的平滑程度。最小化這個(gè)目標(biāo)就等價(jià)于讓我和我的鄰居更加相似。

3、用統(tǒng)一優(yōu)化框架去理解現(xiàn)有 GNN

GNN 大都是在優(yōu)化這一目標(biāo)，我們可以分不同的情況做下討論：

當(dāng)參數(shù) ：

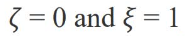
時(shí)優(yōu)化目標(biāo)就變成了：

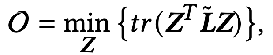
求偏導(dǎo)就得到：

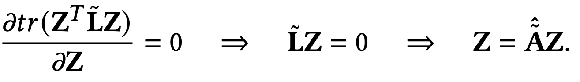
我們?cè)侔焉厦娴玫降慕Y(jié)果做進(jìn)一步的展開(kāi)就能得到：

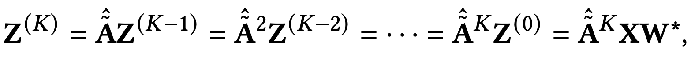
它的意義就表示第 K 層的所有節(jié)點(diǎn)表征等于第 K-1 層的節(jié)點(diǎn)表征在鄰接矩陣上的傳播過(guò)程，一直推導(dǎo)到最后就會(huì)發(fā)現(xiàn)就等于初始的特征 X 做完特征變換 W* 之后在鄰接矩陣上傳播 K 次。其實(shí)這就是去掉了非線性層的 GCN 或者 SGC 的模型。

當(dāng)參數(shù) F₁=F₂=I，ζ=1，ξ=1/α-1，α∈（0,q] ，且選擇全通的濾波器時(shí)優(yōu)化目標(biāo)就變成了：

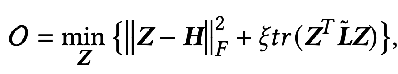
這時(shí)我們同樣對(duì) Z 求偏導(dǎo)，并令偏導(dǎo)等于 0 就可以得到優(yōu)化目標(biāo)的閉式解：

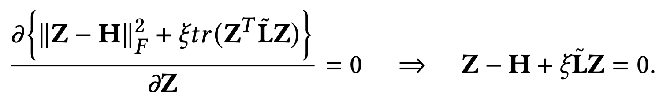
對(duì)結(jié)果稍作轉(zhuǎn)換就可以得到下面的式子：

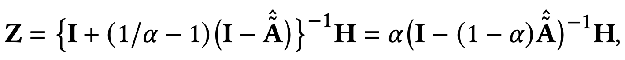
我們可以發(fā)現(xiàn)上面的式子就代表了節(jié)點(diǎn)特征在個(gè)性化 PageRank 上傳播的過(guò)程，也就是 PPNP 模型。

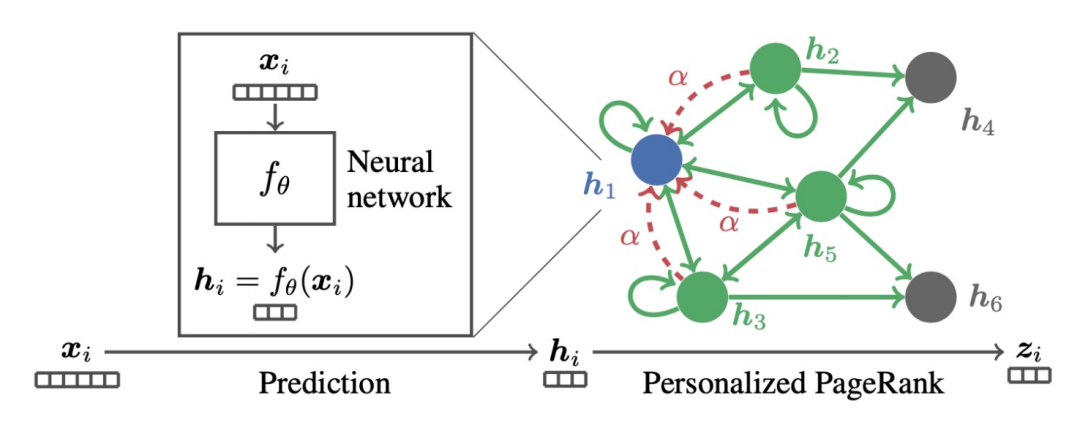
同樣是這樣一個(gè)模型，如果用梯度下降的方式去求，并且設(shè)置步長(zhǎng)為 b，迭代項(xiàng)是 k-1時(shí)刻目標(biāo)函數(shù)對(duì) Z 的偏導(dǎo)值。

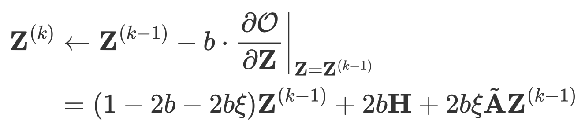
當(dāng)

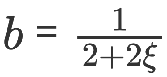
時(shí)可以得到：

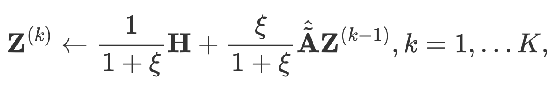
這就是 APPNP 模型。APPNP 模型的出現(xiàn)背景是 PPNP 模型中求矩陣的逆運(yùn)算太過(guò)復(fù)雜，而 APPNP 使用迭代近似的手段去求解。也可以理解 APPNP 能收斂到 PPNP 是因?yàn)閮烧邅?lái)源自同一個(gè)框架。

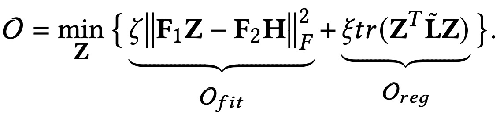
4、新的 GNN 框架

只要我們?cè)O(shè)計(jì)一個(gè)新的擬合項(xiàng) O_fit，并設(shè)計(jì)一個(gè)對(duì)應(yīng)的圖正則項(xiàng) O_reg，再加上一個(gè)新的求解過(guò)程就可以得到一個(gè)新的 GNN 模型。

① 例子1：從全通濾波到低通濾波

前面講到過(guò)，全通濾波器下卷積核 F₁=F₂=I ，當(dāng)卷積核為拉普拉斯矩陣 L 時(shí)就是高通濾波器。如果將這兩種情況加權(quán)得到的 GNN 能 encode 低通的信息：

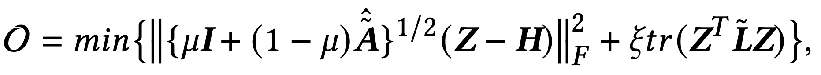
當(dāng)

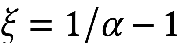
可以得到精確解：

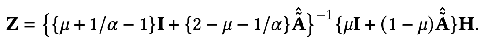
同樣，我們可以迭代求解：

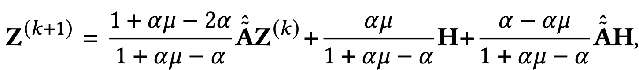
5、Elastic GNN

前面的統(tǒng)一框架中提到的正則項(xiàng)相當(dāng)于 L2 正則，相當(dāng)于計(jì)算圖上任意兩個(gè)點(diǎn)之間的差異信息。有研究者覺(jué)得 L2 正則過(guò)于全局化，會(huì)導(dǎo)致整個(gè)圖上的平滑程度趨于相同，這與實(shí)際并不完全一致。于是就提出加入 L1 正則項(xiàng)，L1 正則項(xiàng)會(huì)對(duì)圖上變化比較大的地方懲罰比較小。

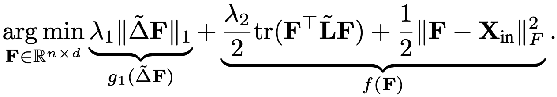
其中的 L1 正則項(xiàng)部分為：

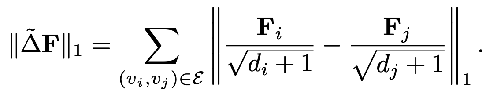
總之，上面的這個(gè)統(tǒng)一框架告訴我們：

我們可以用一個(gè)更宏觀的視角去理解 GNN
我們可以從這個(gè)統(tǒng)一框架出發(fā)去設(shè)計(jì)新的 GNN

但是，這個(gè)統(tǒng)一框架還只能適配于同質(zhì)圖結(jié)構(gòu)，接下來(lái)我們看一下更加普遍的多關(guān)系圖的結(jié)構(gòu)。

二、關(guān)系GNN模型

1、RGCN

所謂的多關(guān)系圖指的就是邊的種類(lèi)大于 1 的圖，如下圖所示。

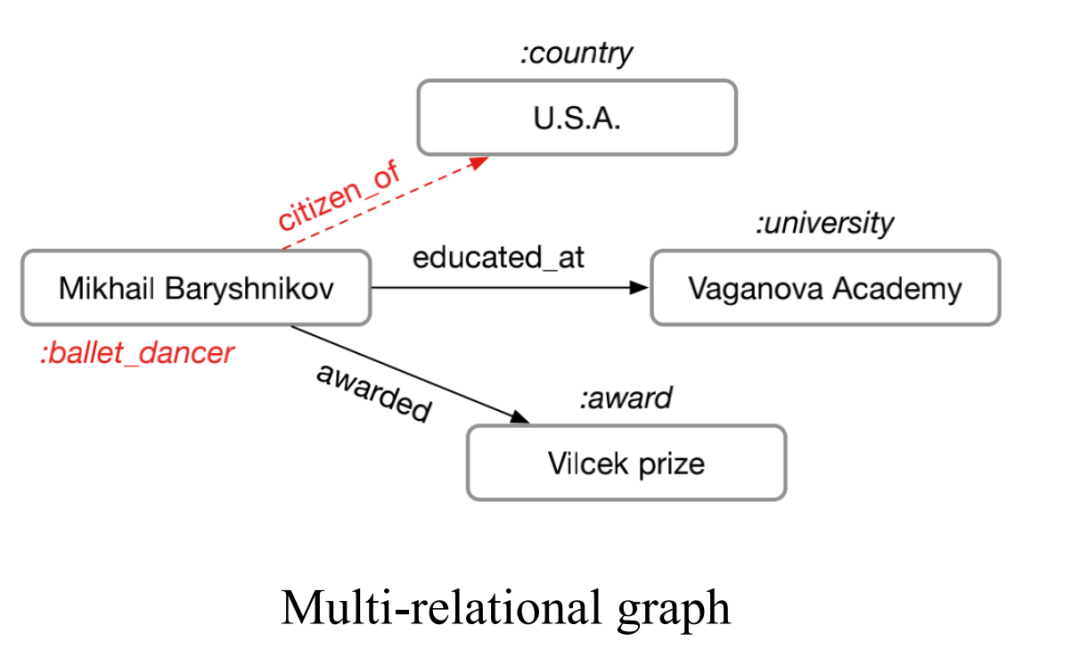
這種多關(guān)系圖在現(xiàn)實(shí)世界中非常廣泛，比如化學(xué)分子中的多類(lèi)型的分子鍵，又如社交關(guān)系圖中人與人的不同關(guān)系。對(duì)于這樣的圖我們可以使用 Relational Graph Neural Networks 來(lái)建模。其主要思想是將具有 N 種關(guān)系的圖單獨(dú)聚合，從而得到 N 個(gè)聚合結(jié)果，再將 N 個(gè)結(jié)果聚合。

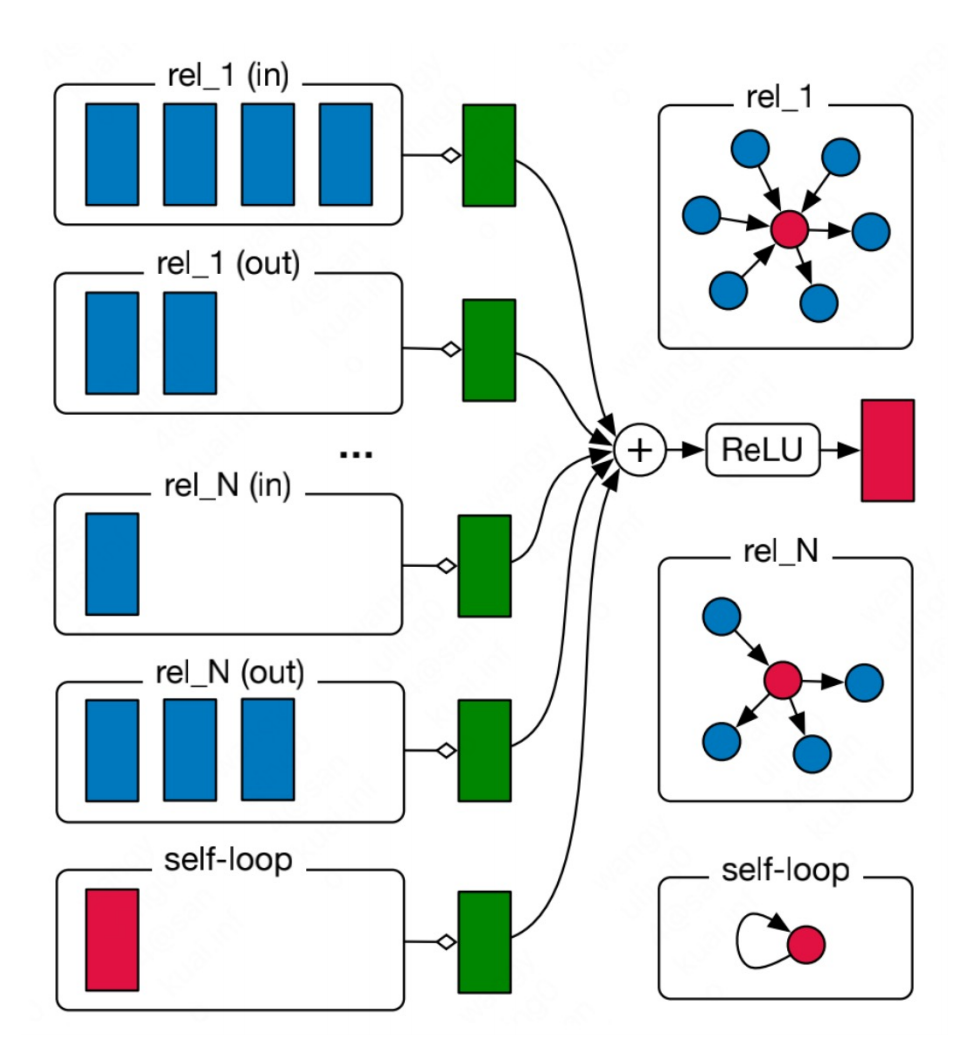
用公式表示就是：

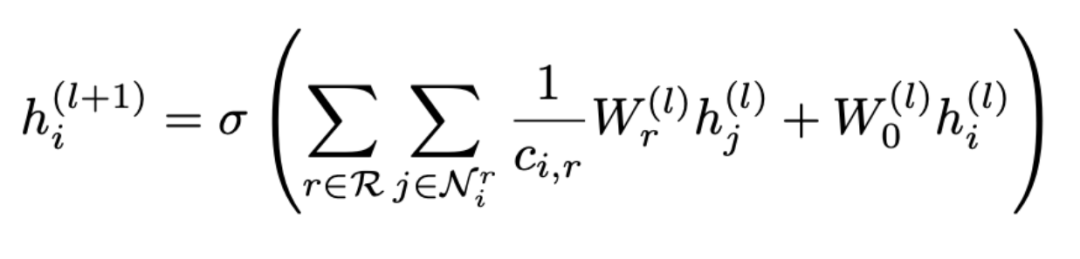
可以看到聚合分兩步進(jìn)行，先從所有的關(guān)系 R 中選擇一種關(guān)系 r，再找到包含這種關(guān)系的所有節(jié)點(diǎn) N^r進(jìn)行聚合，其中 W^r是用來(lái)加權(quán)各種關(guān)系的權(quán)重。因此可以看到隨著圖中關(guān)系數(shù)目的增加，權(quán)重矩陣 W^r也會(huì)跟著增加，這樣就會(huì)導(dǎo)致過(guò)度參數(shù)化的問(wèn)題（Over-parameterization）。另外，將拓?fù)潢P(guān)系圖根據(jù)關(guān)系拆分的做法也會(huì)導(dǎo)致過(guò)平滑（Over-smoothing）。

2、CompGCN

為了解決過(guò)度參數(shù)化的問(wèn)題，CompGCN 用了一個(gè)向量化的關(guān)系編碼器來(lái)代替 N 個(gè)關(guān)系矩陣：

編碼器包含正向、反向、自環(huán)三種方向的關(guān)系：

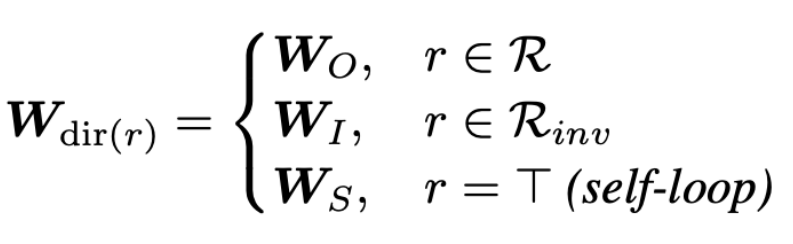
每一次迭代也都會(huì)對(duì) relation 的 embedding 進(jìn)行更新。

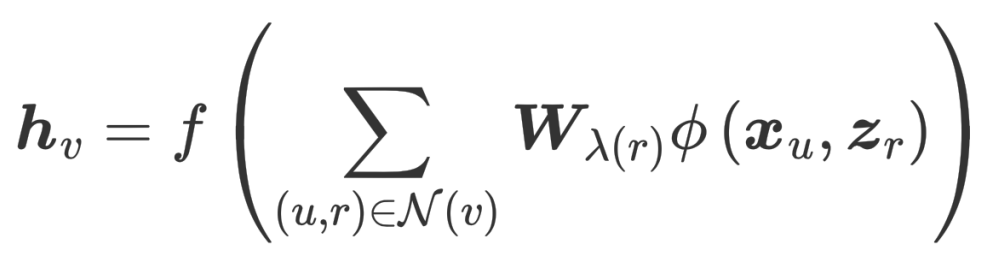
但這種啟發(fā)式的設(shè)計(jì)，以及這樣的參數(shù)化編碼器同樣也會(huì)造成過(guò)度的參數(shù)化。那么，基于上面的考慮就得到了我們工作的出發(fā)點(diǎn)：能否從優(yōu)化目標(biāo)的角度去設(shè)計(jì)一個(gè)更加可靠的 GNN，同時(shí)能夠解決現(xiàn)有 GNN 存在的問(wèn)題。

三、集成多關(guān)系圖神經(jīng)網(wǎng)絡(luò)

我們的 EMR GNN 在今年發(fā)表，接下來(lái)主要從三個(gè)方面展開(kāi)討論我們?nèi)绾卧O(shè)計(jì)一個(gè)適用于多關(guān)系圖的 GCN：

如何設(shè)計(jì)一個(gè)合適的集成優(yōu)化算法
消息的傳遞機(jī)制
GNN 模型是怎么設(shè)計(jì)的

1、集成優(yōu)化算法

這個(gè)優(yōu)化算法需要滿(mǎn)足兩方面要求：

能夠同時(shí)捕捉圖上的多種關(guān)系
能夠建模出圖上不同關(guān)系的重要性

我們?cè)诙嚓P(guān)系圖上提出的集成的多關(guān)系圖正則項(xiàng)如下：

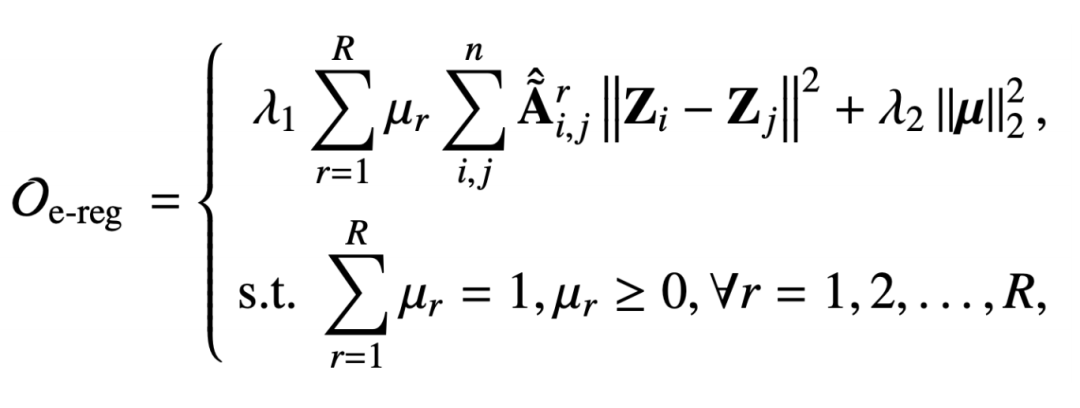
這個(gè)正則項(xiàng)也是要去捕捉圖信號(hào)的平滑能力，只不過(guò)這個(gè)鄰接矩陣是在關(guān)系 r 下去捕獲的，而受歸一化約束的參數(shù) μ_r則是為了建模某種關(guān)系的重要程度。而第二項(xiàng)是系數(shù)向量的二范式正則，是為了讓系數(shù)向量更加均勻。

而為了解決過(guò)平滑的問(wèn)題我們又加了一個(gè)擬合項(xiàng)，來(lái)保證原始的特征信息不被丟失。擬合項(xiàng)與正則項(xiàng)加起來(lái)就是：

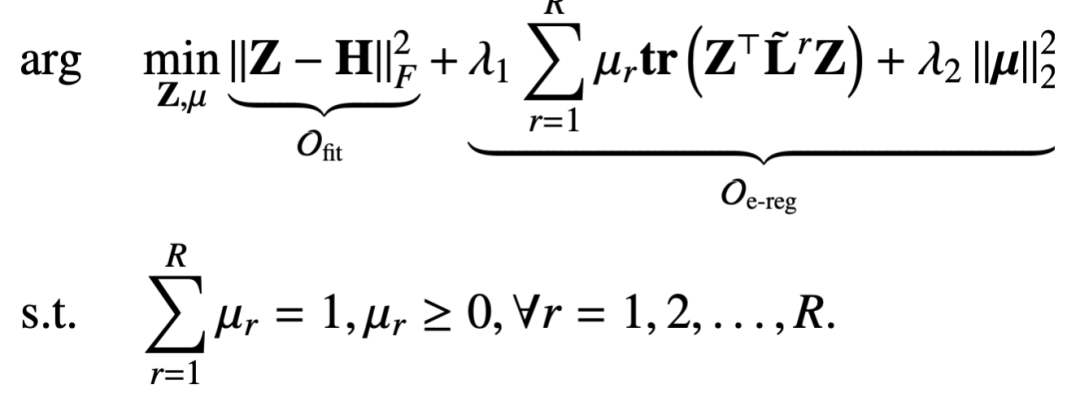
和上一章提到的統(tǒng)一框架相比，我們這里設(shè)計(jì)的目標(biāo)函數(shù)包含節(jié)點(diǎn)矯正 Z 和關(guān)系矩陣參數(shù) μ 兩個(gè)變量。那么基于這樣一個(gè)優(yōu)化目標(biāo)去推導(dǎo)得到一個(gè)消息傳播機(jī)制也是一個(gè)挑戰(zhàn)。

2、推導(dǎo)消息傳遞機(jī)制

在這里我們采用的是一個(gè)迭代優(yōu)化的策略：

先固定節(jié)點(diǎn)表征 Z，再去優(yōu)化參數(shù) μ
根據(jù)上一步迭代的結(jié)果 μ 再去優(yōu)化節(jié)點(diǎn)表征 Z

當(dāng)固定節(jié)點(diǎn)表征 Z 時(shí)，整個(gè)優(yōu)化目標(biāo)就退化成只跟 μ 相關(guān)的一個(gè)目標(biāo)函數(shù)，但是這是一個(gè)帶約束的目標(biāo)函數(shù)：

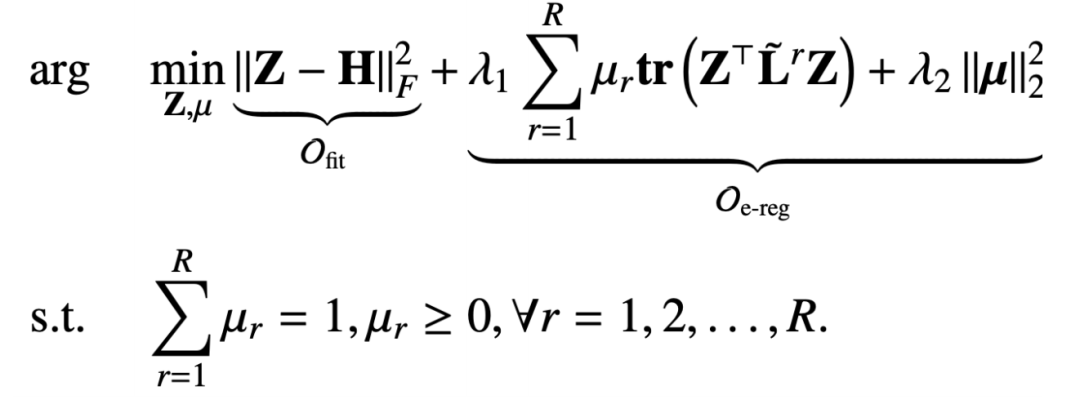
這其實(shí)是一個(gè)單純形約束（constraint in a standard simplex）上的一個(gè) μ 的convex函數(shù)，對(duì)于這類(lèi)問(wèn)題我們可以使用鏡像熵梯度下降算法（Mirror Entropic Descent Algorithm）去解決。我們會(huì)先求出一個(gè)常量，然后對(duì)每一種關(guān)系下的權(quán)重系數(shù)進(jìn)行更新，整個(gè)更新的過(guò)程類(lèi)似于指數(shù)的梯度下降算法。

固定關(guān)系系數(shù) μ 去更新 Z，這時(shí)的優(yōu)化目標(biāo)就退化成下面這種形式：

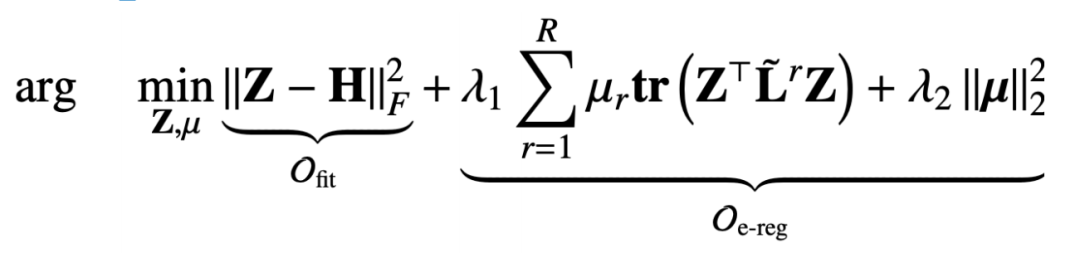
這樣我們求目標(biāo)函數(shù)對(duì) Z 的偏導(dǎo)數(shù)，并令偏導(dǎo)數(shù)等于 0 就可以得到：

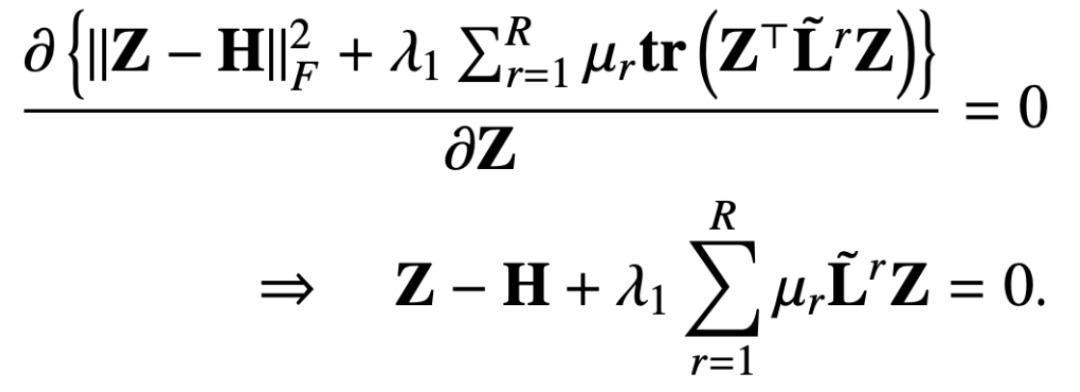
那么 Z 的閉式解就是：

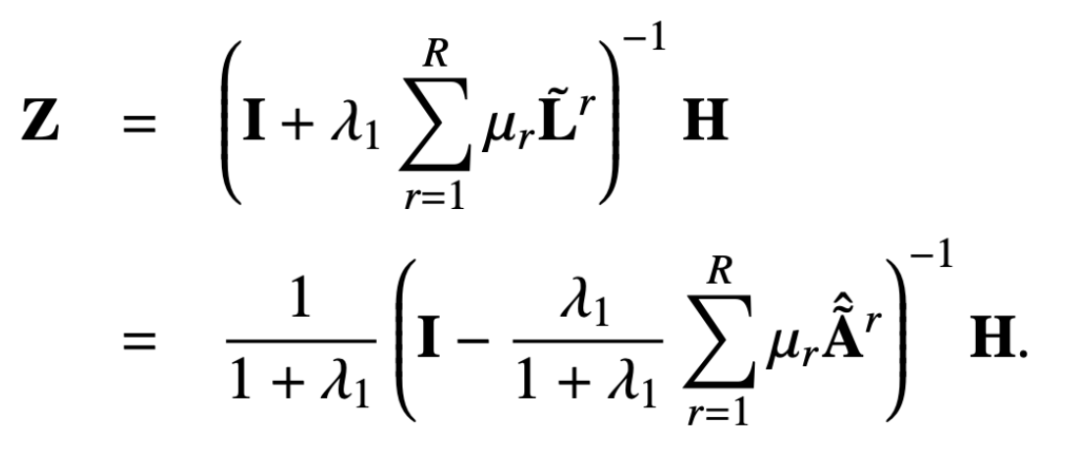
同樣我們可以用迭代的方式去得到近似解，這一過(guò)程可以表示如下：

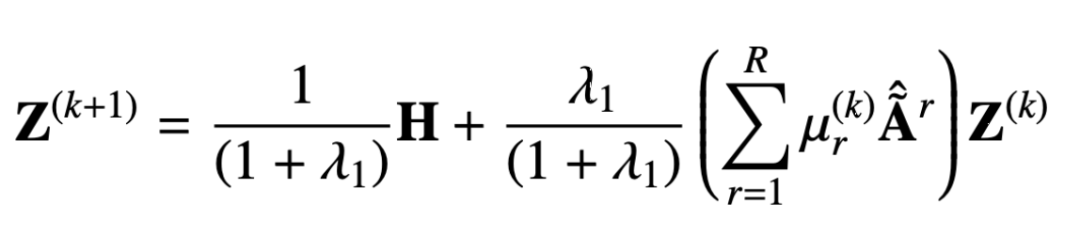
從推導(dǎo)出的消息傳遞機(jī)制中我們可以證明該設(shè)計(jì)可以避免過(guò)度平滑，避免過(guò)度參數(shù)化，下面我們可以看下證明的過(guò)程。

原始的多關(guān)系 PageRank 矩陣是這樣定義的：

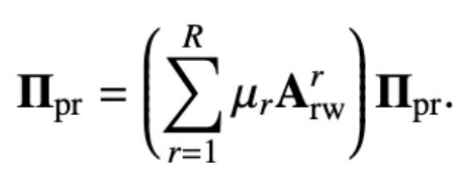
個(gè)性化的多關(guān)系 PageRank 矩陣在此基礎(chǔ)上加了一個(gè)返回自身節(jié)點(diǎn)的概率：

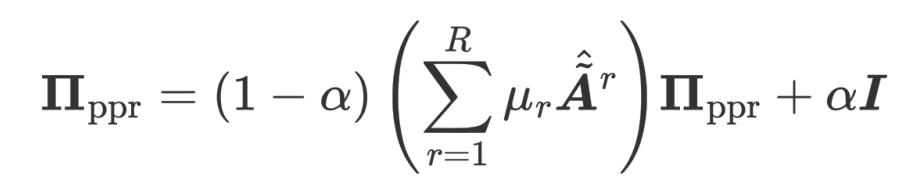
通過(guò)解上面的循環(huán)等式就可以得到多關(guān)系個(gè)性化 PageRank 矩陣：

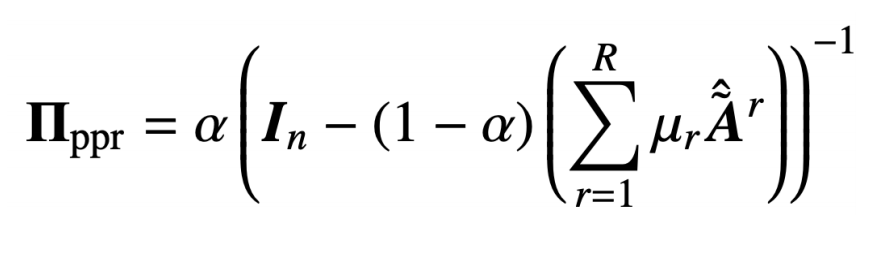
我們讓 :

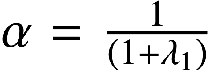
就可以得到：

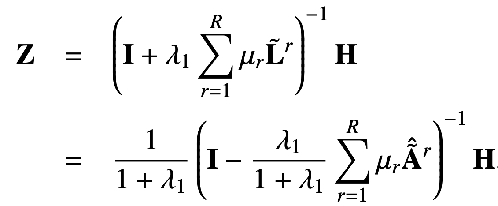
這個(gè)也就是我們提出方案所得到的閉式解。也就是說(shuō)我們的傳播機(jī)制可以等價(jià)于特征 H 在節(jié)點(diǎn)的個(gè)性化 PageRank 矩陣上進(jìn)行傳播。因?yàn)檫@個(gè)傳播機(jī)制中一個(gè)節(jié)點(diǎn)可以有一定的概率返回自身節(jié)點(diǎn)，也就是說(shuō)在信息傳遞過(guò)程中不會(huì)丟失自身信息，從而防止過(guò)度平滑的問(wèn)題。

另外，我們這個(gè)模型也緩解了過(guò)度參數(shù)化這一現(xiàn)象，因?yàn)閺墓街锌梢钥吹剑瑢?duì)于每一種關(guān)系我們的模型只有一個(gè)可學(xué)習(xí)的系數(shù) μ_r，相比于之前的 encoder，或者是權(quán)重矩陣 w_r 的參數(shù)量來(lái)比，我們這種參數(shù)量級(jí)幾乎是可以忽略不計(jì)的。下圖即為我們?cè)O(shè)計(jì)的模型架構(gòu)：

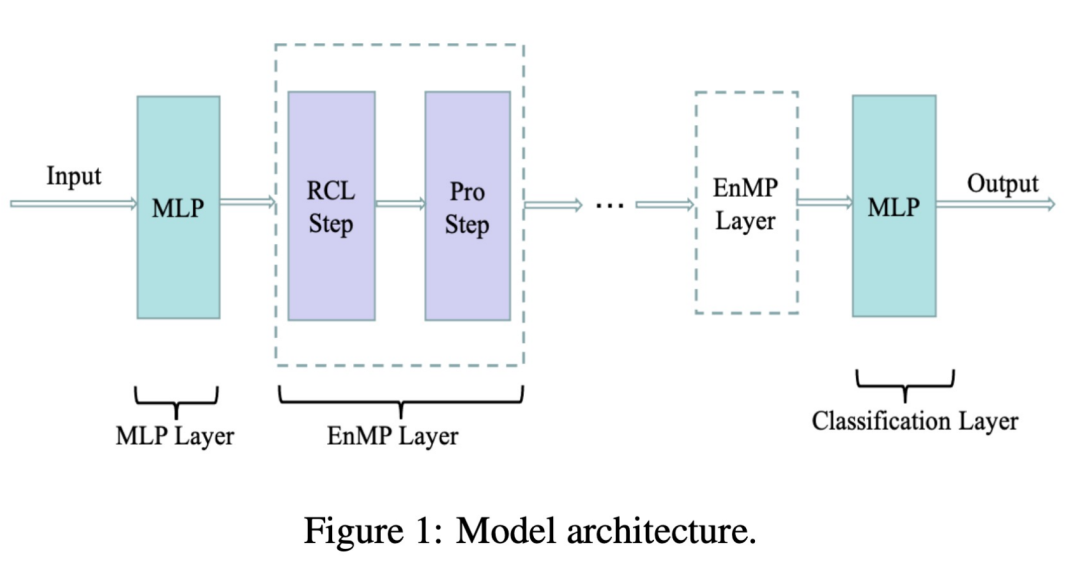
其中 RCL 即為參數(shù)學(xué)習(xí)的步驟，而 Pro 步驟為特征傳播的步驟。這兩個(gè)步驟放在一起就構(gòu)成了我們的消息傳遞層。那么怎樣把我們的消息傳遞層整合到 DNN 中，且不引入額外的更多參數(shù)呢？我們也沿用了解耦的設(shè)計(jì)思路：先用一個(gè) MLP 對(duì)輸入特征進(jìn)行提取，之后經(jīng)過(guò)多層我們所設(shè)計(jì)的的消息傳遞層，疊加多層同樣不會(huì)導(dǎo)致過(guò)平滑。最終的傳遞結(jié)果經(jīng)過(guò) MLP 完成節(jié)點(diǎn)分類(lèi)即可做下游的任務(wù)。用公式將上述過(guò)程表示如下：

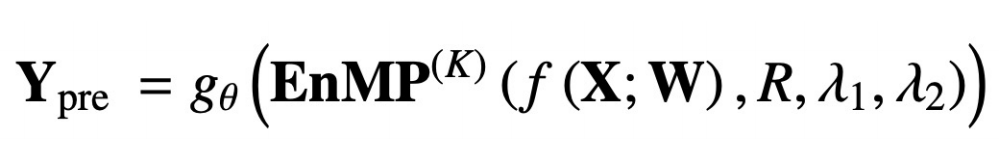
f(X;W) 就表示將輸入特征經(jīng)過(guò) MLP 做特征提取，后面的 EnMP(K) 則表示將提取結(jié)果經(jīng)過(guò) K 層的的消息傳遞，g_θ則表示經(jīng)過(guò)一個(gè)分類(lèi)的 MLP。

反向傳播中我們只用更新兩個(gè) MLP 中的參數(shù)即可，而我們的 EnMP 中的參數(shù)是在前向傳播過(guò)程中學(xué)習(xí)的，后向傳播過(guò)程中不用更新 EnMP 任何的參數(shù)。

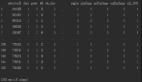
我們可以對(duì)比看下不同機(jī)制的參數(shù)量，可以看到我們的 EMR-GNN 的參數(shù)量主要來(lái)自于前后兩個(gè) MLP，以及 relation 的系數(shù)。當(dāng)層數(shù)大于 3 時(shí)我們就可以知道 EMR-GNN 的參數(shù)量比 GCN 的參數(shù)量還要少，更是比其他異質(zhì)圖還要的少了。

在這么少的參數(shù)量下我們的 EMR-GNN 在如下不同的節(jié)點(diǎn)分類(lèi)任務(wù)下還是可以達(dá)到最好的水平。

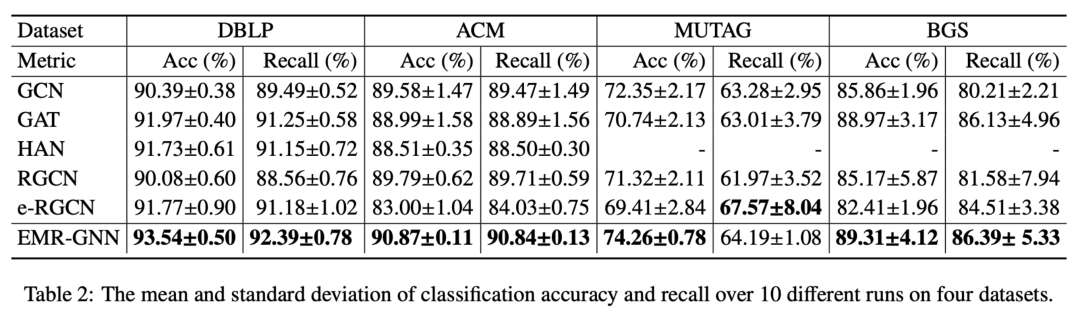
此外，我們還對(duì)比了不同的網(wǎng)絡(luò)結(jié)構(gòu)在層數(shù)增加后分類(lèi)精度的變化，如下圖所示，當(dāng)當(dāng)層數(shù)增加到 64 層后我們的模型依然能夠保持較高的精度，而原始的 RGCN 當(dāng)層數(shù)增加到 16 層以上時(shí)就會(huì)遇到內(nèi)存不夠的情況，想要迭加更多層更是不可能的，這就是由于其參數(shù)過(guò)多導(dǎo)致的。而 GAT 模型則由于過(guò)平滑而表現(xiàn)性能降低。

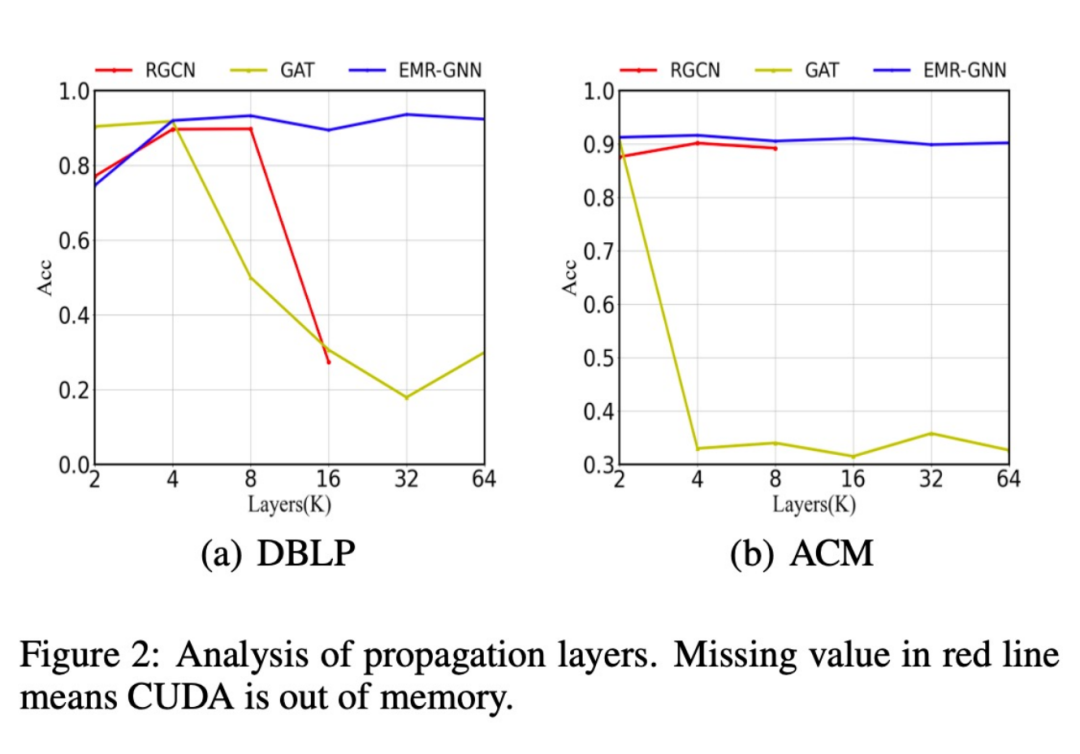
此外我們還發(fā)現(xiàn)，我們的 EMR-GNN 在較小的數(shù)據(jù)規(guī)模下即可達(dá)到全樣本的分類(lèi)精度，而RGCN 則下降很多。

我們還分析了 EMR-GNN 所學(xué)習(xí)到的關(guān)系系數(shù)μr是否真的有意義，那么什么算有意義呢？我們希望關(guān)系系數(shù) μ_r關(guān)系系數(shù)給重要的關(guān)系以更大的權(quán)重，給不重要的關(guān)系以更小的權(quán)重。我們分析的結(jié)果如下圖所示：

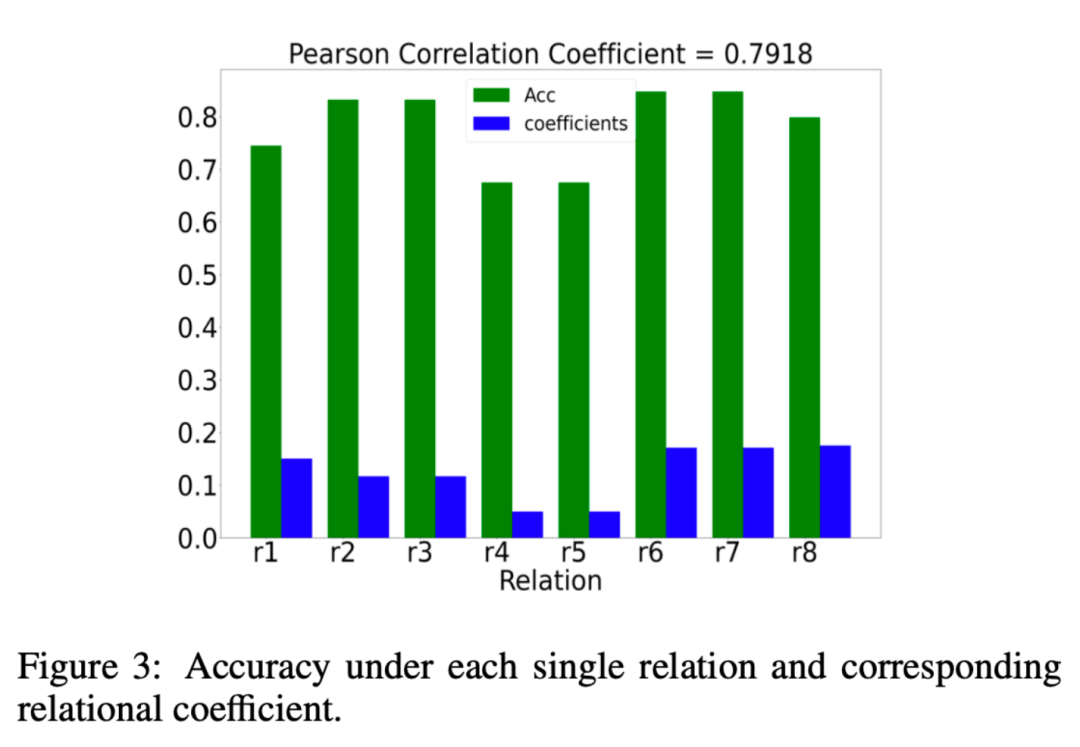
其中綠色的柱狀圖表示在一種關(guān)系下分類(lèi)時(shí)的效果，如果在某種關(guān)系下其分類(lèi)精度更高，我們就可以認(rèn)為該關(guān)系時(shí)重要的。而藍(lán)色柱子則表示我們的 EMR-GNN 所學(xué)習(xí)到的關(guān)系系數(shù)。藍(lán)綠對(duì)比可以看到我們的關(guān)系系數(shù)能夠反映出關(guān)系的重要程度。

最后我們也做了一個(gè)可視化展示如下圖所示：

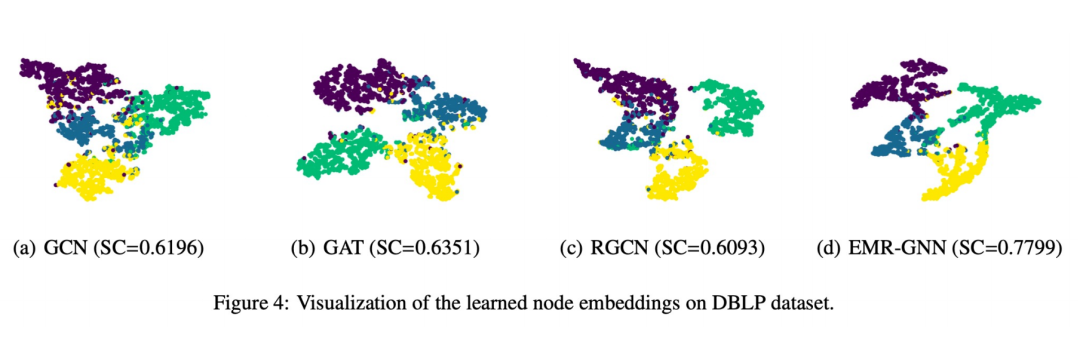
可以看到 EMR-GNN 訓(xùn)練出來(lái)的節(jié)點(diǎn) embedding 能夠帶有節(jié)點(diǎn)的結(jié)構(gòu)化信息，它能夠讓同一類(lèi)的節(jié)點(diǎn)更加內(nèi)聚，不同類(lèi)的盡可能分開(kāi)，分割邊界相對(duì)其他網(wǎng)絡(luò)更清晰。

四、總結(jié)

1. 我們用統(tǒng)一的視角去理解 GNN

① 在這個(gè)視角下我們可以容易看出現(xiàn)有 GNN 有什么問(wèn)題

②這個(gè)統(tǒng)一視角可以給我們一個(gè)重新設(shè)計(jì) GNN 的基礎(chǔ)

2. 我們從目標(biāo)函數(shù)的角度嘗試設(shè)計(jì)一個(gè)新的多關(guān)系的 GNN

① 我們首先設(shè)計(jì)了一個(gè)集成的優(yōu)化框架

② 基于這樣一個(gè)優(yōu)化框架我們推導(dǎo)出來(lái)了一個(gè)消息傳遞機(jī)制

③ 這個(gè)帶有少量參數(shù)的消息傳遞機(jī)制簡(jiǎn)單地與 MLP 結(jié)合即可得到 EMR-GNN

3. EMR-GNN 有什么好處？

① 它依靠一個(gè)可靠的優(yōu)化目標(biāo)，因此得到的結(jié)果可信，從數(shù)學(xué)上也可以解釋其底層的原理

② 它可以解決現(xiàn)有的 Relation GNN 的過(guò)平滑問(wèn)題

③ 解決過(guò)參數(shù)化問(wèn)題

④ 容易訓(xùn)練、在更小的參數(shù)量下可得到較好的效果

五、Q&A環(huán)節(jié)

Q1：關(guān)系系數(shù)的學(xué)習(xí)與 attention 機(jī)制有什么區(qū)別嗎？

A1：這里的關(guān)系系數(shù)學(xué)習(xí)是通過(guò)優(yōu)化框架推導(dǎo)出來(lái)的更新過(guò)程，而 attention 是需要基于反向傳播才能學(xué)習(xí)到的過(guò)程，所以說(shuō)在優(yōu)化上兩者就有本質(zhì)不同。

Q2：在大規(guī)模數(shù)據(jù)集上模型的適用性如何？

A2：我們?cè)诟戒浿蟹治隽四Ｐ偷膹?fù)雜度，從復(fù)雜度上說(shuō)我們和 RGCN 是一個(gè)量級(jí)的，但是參數(shù)量會(huì)比 RGCN 更少，因此我們的模型更是適用于大規(guī)模數(shù)據(jù)集。

Q3：這個(gè)框架能融入邊的信息嗎？

A3：可以在擬合項(xiàng)或者正則項(xiàng)中融入。

Q4：這些數(shù)學(xué)基礎(chǔ)應(yīng)該從哪里學(xué)？

A4：一部分是基于前人的工作，另外一部分優(yōu)化相關(guān)的數(shù)學(xué)理論我們用的也是一些比較經(jīng)典的優(yōu)化方面論文。

Q5：關(guān)系圖和異構(gòu)圖的區(qū)別在什么地方？

A5：關(guān)系圖是一種異構(gòu)圖，只不過(guò)異構(gòu)圖我們都通常認(rèn)為是哪些節(jié)點(diǎn)的類(lèi)型或者邊的類(lèi)型大于 1 的。而關(guān)系圖我們特別關(guān)注的是關(guān)系的類(lèi)別大于 1，可以理解后者包括前者。