Hash表、快排與二分查找:兩數之和
大家好,我是小風哥。
我在這個公眾號寫過很多計算機底層方向的文章,應許多讀者的要求,從這篇文章起我們開始一個新的系列:數據結構與算法,原來的計算機底層方向也會繼續更新。
數據結構與算法系列的前期以LeetCode題解為例來講解,當到達一定量后總結程序員必備的算法思想以及必備的數據結構知識,這個系列的目的是讓你:看得懂、學得會、寫得出。
也歡迎大家在留言區打卡,準備春招的同學可以一起刷起來。
廢話少說,開始今天的題目,這是數據結構與算法之LeetCode刷題系列第1篇。
今天的題目是兩數之和,題目是這樣的:
給定一個整數數組與一個target,在數組中找到兩個數,其和等于target,并返回這兩個數字的下標。
示例:
數組 nums = [2,7,11,15], target = 9,則輸出[0,1],因為nums[0] + nums[1] == 9
題目不難,解決方法也有很多種,我們依次來看一下,任何題目都可以從最簡單的方法開始去想,以下代碼均為C++。
暴力解法
我們首先固定一個數字,比如第一個數字2,然后遍歷后面的元素,判斷是否相加等于9,有就記錄下來,沒有則看下一個數字,也就是7,最終代碼非常簡單,其時間復雜度為O(n^2):
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
for (int i = 0; i < nums.size(); i++) {
for (int j = i + 1; j < nums.size(); j++) {
if (nums[i] + nums[j] == target) {
res.push_back(i);
res.push_back(j);
}
}
}
return res;
}
萬萬沒想到的是這樣的代碼竟然可以AC(AC是刷題的常用術語,也就是Accept,通過代碼的評測標準,包括正確性、耗時、內存的消耗等等)。
從這里的分析我們其實可以知道,這本質上其實是一個搜索問題,假如我知道第一個數字是2,而target是9,那么我們需要回答“這個數組中是否有7這個數字”,因此這本質上是一個搜索問題。
既然是搜索問題,那么hash表顯然是我們最得力的武器。
hash 表
關于hash表后續會有專題詳解。
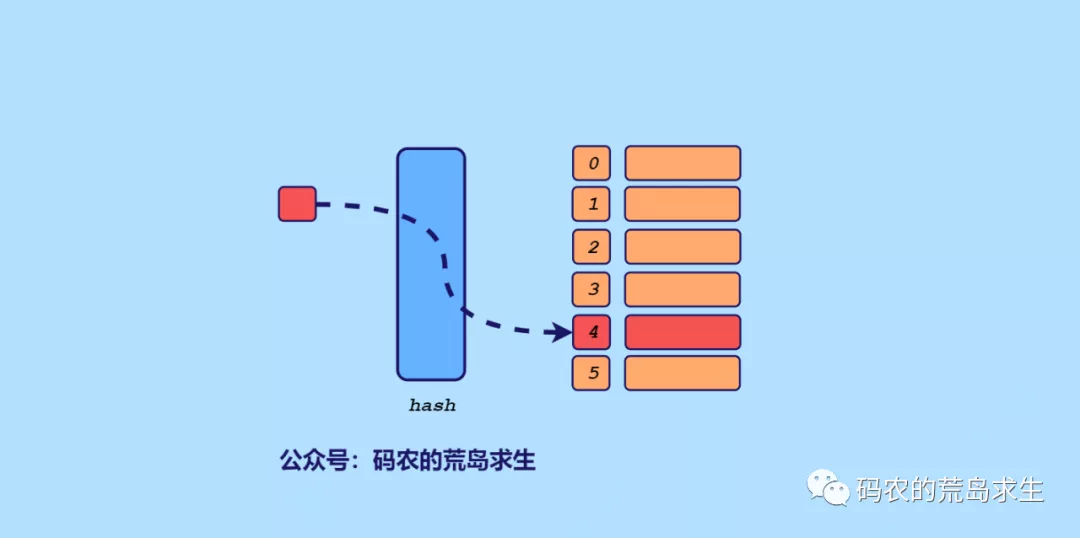
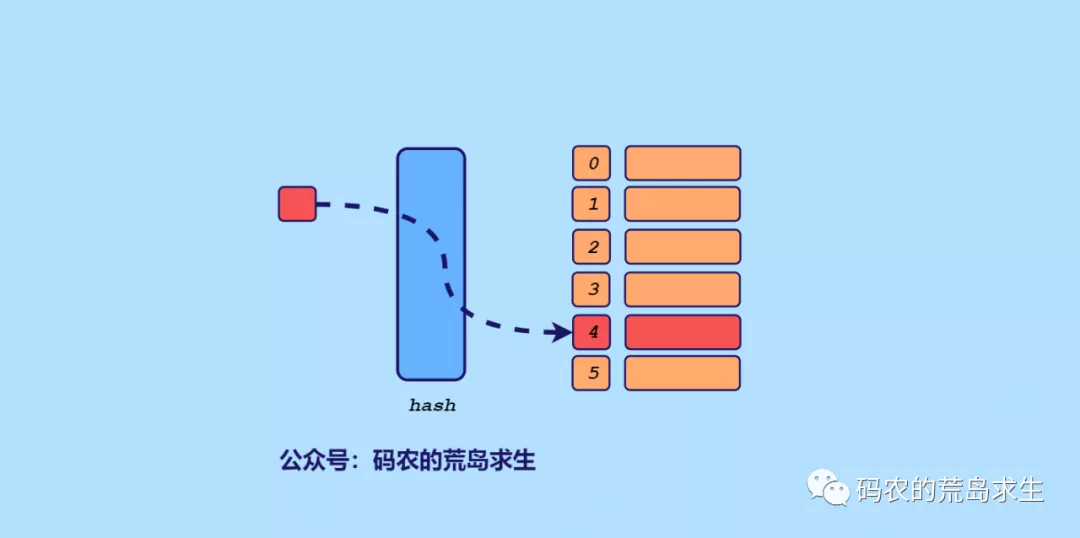
C++中基于hash表這種數據結構的是std::unordered_map,我們的思路也很簡單,把所有的數組元素作為key,數組下標作為值,因為題目要求我們返回下標,因此這里必須把下標也存儲起來,有了這樣的map,剩下的就簡單了。
依次遍歷數組中每個元素N,查找target-N是否存在于map中即可。
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> map;
vector<int> res;
for (int i = 0; i < nums.size(); i++) {
auto iter = map.find(target - nums[i]);
if (iter == map.end()) {
map[nums[i]] = i;
} else {
res.push_back(i);
res.push_back(iter->second);
}
}
return res;
}
顯然,該算法時間復雜度是O(n),因為一般情況下可以認為hash表能常數復雜度下查找到元素。
是不是覺得很簡單,注意,這里使用了map容器,那如果面試官要求你不得借助這種已經寫的庫該怎么辦呢?
我們在文章開頭分析過,這其實本質上是一個搜索問題,既然是搜索問題,那么解決該問題的另一種思路就是排序。
只要排好序剩下的就簡單了,二分查找天然就是有序搜索問題的好幫手。
因此接下來的思路就是排序加二分查找。
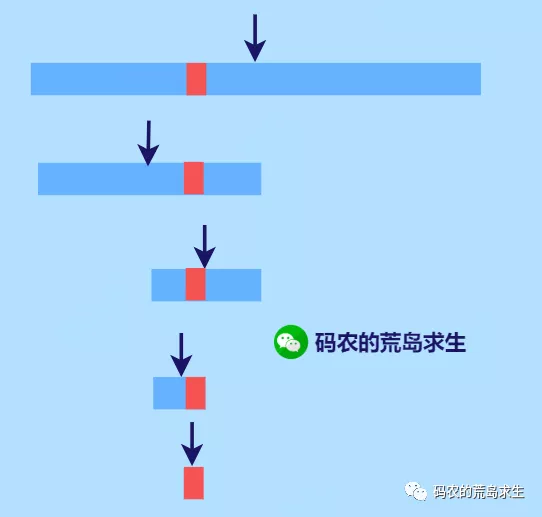
排序加二分查找
思路已經介紹完畢,接下來我們手寫快排,但是我們排誰呢?
注意題目要求返回元素下標,因此排序時需要除了數組元素也需要把下標帶上。
void quick_sort(vector<pair<int,int>>& nums, int b, int e) {
if (b > e) return;
int i = b - 1;
for (int k = b; k < e; k++) {
if (nums[k].second < nums[e].second) {
swap(nums[++i], nums[k]);
}
}
swap(nums[++i], nums[e]);
quick_sort(nums, b, i - 1);
quick_sort(nums, i + 1, e);
}
有的同學可能沒有看懂這里的排序方法,甚至認為快排之類的排序算法只能靠死記硬背,其實不是的,這類經典的排序算法背后都有極其重要的算法思想,比如快排背后的思想其實是divide and conquer,這是另一個龐大的話題,限于篇幅,我們會在后續專題詳解。
現在快排有了,接下來實現二分查找:
int binary_search(vector<pair<int,int>>& nums,
int b, int e, int target) {
while(b <= e) {
int m = (b + e) / 2;
if (nums[m].second == target) {
return nums[m].first;
} else if (nums[m].second < target) {
b = m + 1;
} else {
e = m - 1;
}
}
return -1;
}
二分查找是一個看起來極其容易但寫起來卻極其容易出錯的算法,不信你可以試試看,這里暫時還不打算詳細講解二分,后續還會多次遇到這個算法,當我們積攢了足夠多的示例后將系統介紹這里涉及的快排與二分。
有了這些函數后就可以實現主要邏輯了:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
vector<pair<int, int>> nums_index;
int size = nums.size();
for (int i = 0; i < size; i++) {
nums_index.push_back(pair<int, int>(i, nums[i]));
}
quick_sort(nums_index, 0, size - 1);
for (int i = 0; i < size - 1; i++) {
int r = binary_search(nums_index, i + 1, size - 1,
target - nums_index[i].second);
if (r != -1) {
res.push_back(nums_index[i].first);
res.push_back(r);
}
}
return res;
}
運行一下發現耗時1s左右,雖然也可以AC,但可以看到運行速度其實是很慢的,還是hash表這種解法速度最快。
可以看到,一道題目其實有很多解法,這里涉及到hash、快排與二分查找,后續我們還會多次見到這些方法,而我們在積攢足夠多的示例后會系統性講解這些數據結構與算法。
本文轉載自微信公眾號「碼農的荒島求生」,可以通過以下二維碼關注。轉載本文請聯系碼農的荒島求生公眾號。