計算機科學中最基本的算法之一是二分查找算法。您可以使用兩種方法實現二分查找：迭代方法和遞歸方法。雖然兩種方法具有相同的時間復雜度，但迭代方法在空間復雜度方面要高效得多。

與遞歸方法產生的 O(logn)  相比，迭代方法的空間復雜度為 O(1) 。那么，如何使用 C、C++ 和 Python 中的迭代方法實現二分查找算法呢？

什么是二分查找？

二分查找也稱為折半查找、對數查找或二分法，是一種搜索并返回排序數組中元素位置的算法。將搜索元素與中間元素進行比較。取下限和上限的平均值，您可以找到中間元素。

如果搜索元素大于中間元素，則意味著左側的所有元素都小于搜索元素。因此，控件通過將下限增加到中間元素的下一個位置來移動到數組的右側（如果數組按升序排列）。

同樣，如果搜索元素小于中間元素，則意味著右側的所有元素都大于搜索元素。因此，控件通過將上限更改為中間元素的先前位置來移動到數組的左側。

與線性搜索實現相比，這大大減少了比較的數量，其中比較的數量等于最壞情況下的元素數量。事實證明，此方法對于查找電話簿中的數字或字典中的單詞非常有用。

以下是二分查找算法的示意圖：

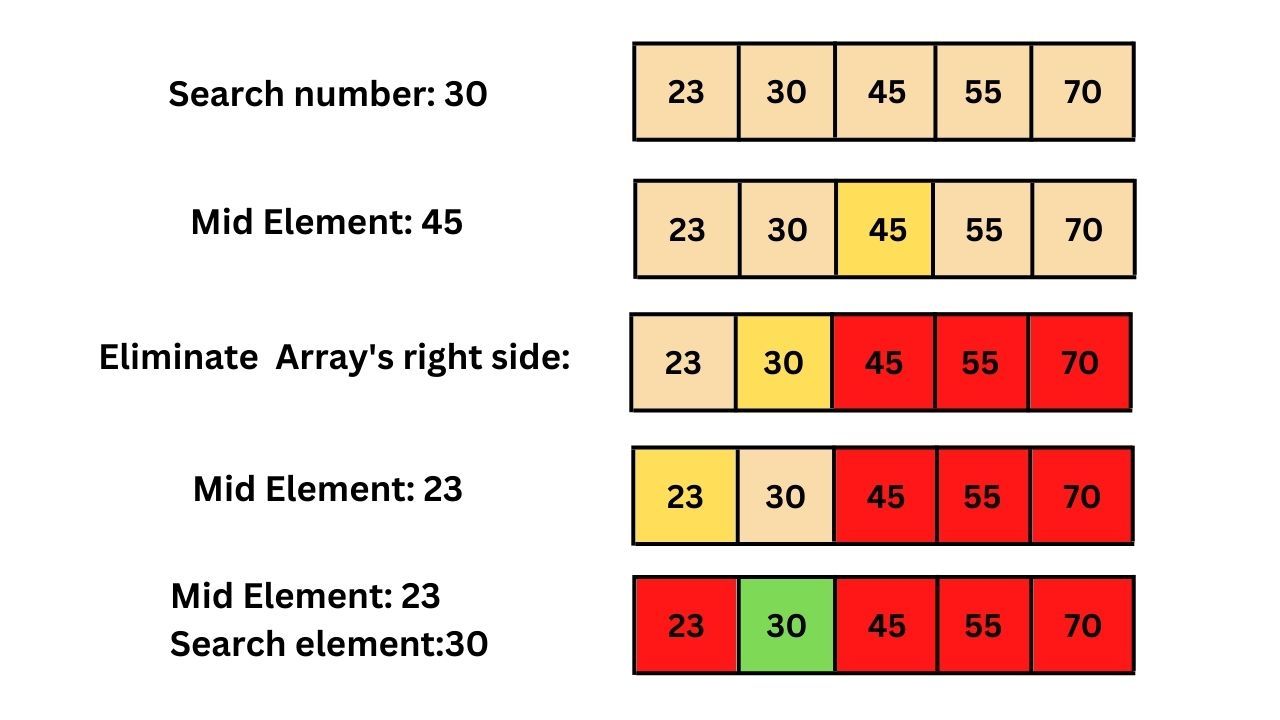
需要 C、C++ 和 Python 實現二分查找的完整源代碼的請加微信：linuxgs。

使用 C 進行二分查找

請按照以下步驟使用 C 實現二分查找：

該程序定義了一個函數 binarySearch()，它返回找到的值的索引或 -1（如果它不存在）：

#include <stdio.h>

int binarySearch(int arr[], int arr_size, int search_number) {
/* ... */
}

該函數通過迭代縮小搜索空間來工作。由于二分查找適用于排序數組，因此您可以計算中間，否則沒有意義。您可以要求用戶提供排序數組，也可以使用排序算法（如氣泡或選擇排序）。

變量 low? 和?high 變量存儲表示當前搜索空間邊界的索引。mid 將索引存儲在中間：

int low = 0, high = arr_size - 1, mid;

主 while() 循環將縮小搜索空間。如果 low?索引的值大于 high 索引，則搜索空間已用盡，因此該值不存在。

while (low <= high) {
/* continues... [1] */
}

return -1;

更新循環開始時的中點后，有三種可能的結果：

• 如果 mid 的值是我們要查找的值，則返回該索引。
• 如果 mid 值大于我們要查找的值，請減小最大值。
• 如果 mid 值較小，則增加low 值。

/* [1] ...continued */
mid = (low + (high - low)) / 2;

if (arr[mid] == search_number)
return mid;
else if (arr[mid] > search_number)
high = mid - 1;
else
low = mid + 1;

使用用戶輸入測試函數。使用 scanf() 從命令行獲取輸入，包括數組大小、內容和要搜索的數字：

int main() {
int arr[100], i, arr_size, search_number;
printf("Enter number of elements: ");
scanf("%d", &arr_size);
printf("Please enter numbers: ");

for (i = 0; i < arr_size; i++) {
scanf("%d", &arr[i]);
}

printf("Enter number to be searched: ");
scanf("%d", &search_number);

i = binarySearch(arr, arr_size, search_number);

if (i==-1)
printf("Number not present");
else
printf("Number is present at position %d", i + 1);

return 0;
}

如果找到該數字，請顯示其位置或索引，否則會顯示一條消息，指出該數字不存在。

使用C++進行二分查找

可以通過導入輸入輸出流將 C 程序轉換為C++程序，并使用命名空間 std 避免在整個程序中多次重復它。

#include <iostream>
using namespace std;

使用 cout 和提取運算符 << 而不是 printf() 和 cin 與插入運算符 >> 而不是 scanf()，你的 C++ 程序就準備好了。

printf("Enter number of elements: ");
cout << "Enter number of elements: ";

scanf("%d", &arr_size);
cin >> arr_size;

使用 Python 進行二分查找

由于 Python 沒有對數組的內置支持，請使用列表。定義一個函數 binarySearch()，它接受三個參數、列表、大小和要搜索的數字：

def binarySearch(arr, arr_size, search_number):
low = 0
high = arr_size - 1
while low <= high:
mid = low + (high-low)//2
if arr[mid] == search_number:
return mid
elif arr[mid] > search_number:
high = mid - 1
else:
low = mid + 1
return -1

初始化兩個變量，low? 和 ?high，作為列表的下限和上限。與 C 實現類似，使用 while 循環來縮小搜索空間。初始化 mid 以存儲列表的中間值。Python 提供了提供最大整數的除法運算符（//）。

進行比較并縮小搜索空間，直到中間值等于搜索編號。如果搜索編號不存在，控件將返回 -1。

arr_size = int(input("Enter number of elements: "))
arr=[]
print("Please enter numbers: ", end=" ")
for i in range(0,arr_size):
arr.append(int(input()))
search_number = int(input("Enter number to be searched: "))
result = binarySearch(arr, arr_size, search_number)

if result == -1:
print("Number not present")
else:
print("Number is present at position ", (result + 1))

使用用戶輸入測試函數。使用 input() 獲取列表大小、其內容和要搜索的數字。使用 int() 將 Python 默認接受的字符串輸入類型轉換為整數。要將數字添加到列表中，請使用 append() 函數。

調用 binarySearch() 并傳遞參數。如果找到該數字，請顯示其位置或索引，否則會顯示一條消息，指出該數字不存在 Number not present。

二分查找算法的輸出

以下是數組中存在元素時二分查找算法的輸出： 

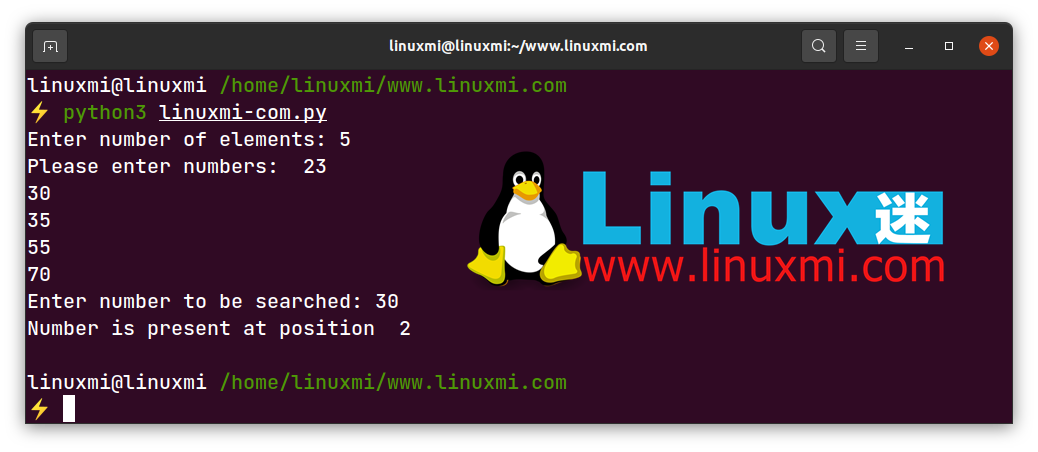
以下是數組中不存在元素時二分查找算法的輸出：

學習基本數據結構和算法

搜索是您學習的第一批算法之一，在編碼競賽、實習和面試中經常被問到。您應該學習的其他一些算法是排序、哈希、動態規劃、字符串匹配和素數測試算法。

此外，了解算法的時間和空間復雜性至關重要。它們是計算機科學中確定任何算法效率的最關鍵概念之一。有了數據結構和算法的知識，你一定會構建最好的程序。