Go 語言算法之美—進階排序
本文轉載自微信公眾號「roseduan寫字的地方」,作者roseduan。轉載本文請聯系roseduan寫字的地方公眾號。
這篇文章再來看看幾種在實踐當中更加常用、也更加復雜一點的排序算法,分別是希爾排序、堆排序、快速排序、歸并排序。
1、希爾排序
希爾排序其實是對插入排序的一種優化,回想一下,插入排序的流程是:將數據分為了已排序區間和未排序區間,依次遍歷未排序區間的值,將其插入到已排序區間合適的位置。
插入排序的一個最大的缺點是:每次只能移動一位,這樣在一些極端的情況下會非常低效;例如數據 2 3 5 7 9 0,如果將 0 移動至元素頭部,需要遍歷整個數組。
希爾排序的優化點就在于此,它的核心思想是將數據中的元素分為了多個組,每一組分別進行插入排序。
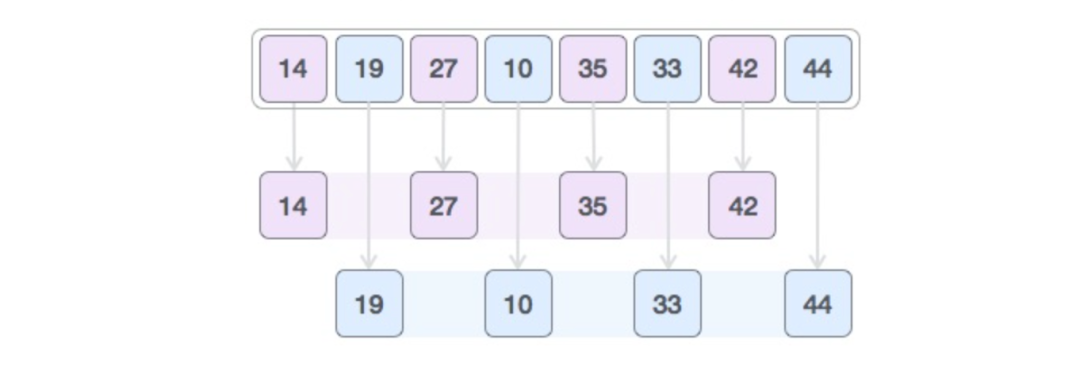
舉一個簡單的例子:有數據 35 33 42 10 14 19 27 44,首先將數據以其長度的 1/2 (也就是 4)為步長,分為了四個組,分別是 {35,14}、{33,19}、{42,27}、{10,44}。
然后對每一組分別進行插入排序,排序后的結果如下:
然后步長縮小一半,變為 2 ,將數組分為了兩個組,分別是 {14,27,35,42}、{19,10,33,44}:
然后再分別對這兩個組進行插入排序,結果就是 14 10 27 19 35 33 42 44。
最后,步長再縮小一半,變為 1,將數組分為了一個組(其實就是數組本身),并再進行插入排序,這樣希爾排序的流程便完成了。
可以看到,希爾排序將數組分為了多個組,其實是為了盡可能的將數據變得局部有序,代碼如下:
- func ShellSort(data []int) {
- length := len(data)
- step := length / 2
- for step >= 1 {
- for i := 0; i < length-step; i++ {
- j, k := i+step, data[i+step]
- for ; j > step-1 && data[j-step] > k; j -= step {
- data[j] = data[j-step]
- }
- data[j] = k
- }
- step /= 2
- }
- }
希爾排序實際應用并不是很多,它的相關復雜度如下:
| Time Complexity | |
| Best | O(nlog n) |
| Worst | O(n2) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | no |
2、堆排序
要理解堆排序,必須得先明白什么是二叉堆。二叉堆(以下簡稱堆)是一種很優雅的數據結構,它是一種特殊的二叉樹,滿足二叉樹的兩個特性便可以叫做堆:
- 是一個完全二叉樹
- 堆中任意一個節點的值都必須大于等于(或者小于等于)其子樹中的所有節點值
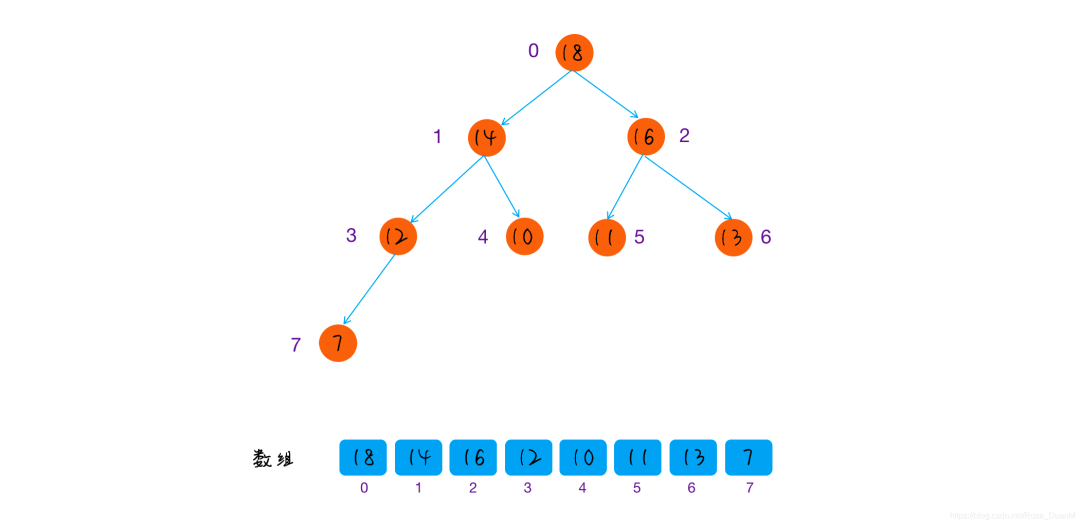
對于節點大于等于子樹中節點值的堆,叫做大頂堆,反之則叫做小頂堆,以下是兩個堆的例子:
從定義和上圖中可以看到,堆的一個特點是,堆頂元素就是堆中最大(或最小)的元素。
堆其實可以使用數組來存儲,堆頂元素就是數組的第一個元素,并且對于任意下標為 i 的節點,其左子節點是 2 * i + 1,右子節點是 2 * i + 2,有了這個對應關系,堆在數組中的存儲就是這樣的:
理解了什么是堆之后,接下來進入正題,看看如何基于堆實現排序。堆排序的步驟一般有兩個,分別是構造堆和排序,下面依次介紹。
構造堆
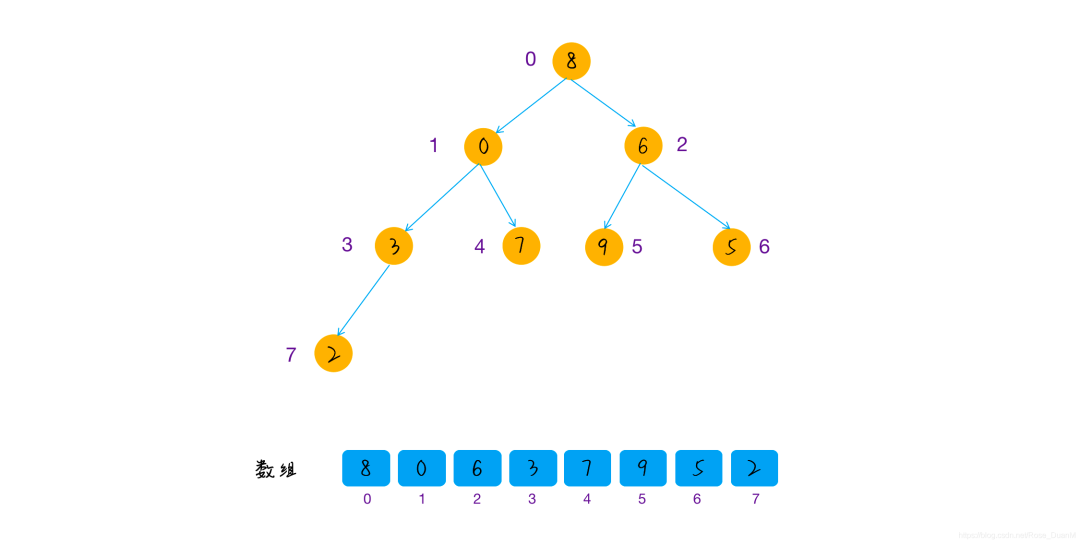
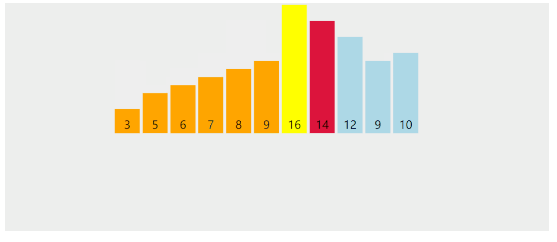
構造堆指的是將無序的數組構造成堆(這里使用大頂堆進行講解),使其符合堆的特征,舉一個例子,對于一個完全無序的數組,其原始狀態和存儲結構如下圖:
要使其變成大頂堆,我們可以這樣做:從第一個非葉子節點開始,依次將其和子節點的值進行比較,如果小于子節點的值,交換節點順序,然后再依次比較下去,直到葉子節點。
這樣就能夠始終滿足堆的特性,任意節點的值總是大于其子樹中所有節點的值。
排序
堆構建完成之后就是排序了,前面提到了堆有一個很重要的特性,那就是堆頂元素就是最大的元素,我們遍歷數組的長度,每次都取堆頂的元素(下標為 0 的元素),將其和數組最后的元素交換位置,然后重新將剩下的數據組織成堆,繼續取堆頂的最大元素,以此類推。
將兩個步驟結合起來,就是堆排序的完整實現了,代碼如下:
- // 堆排序
- func HeapSort(data []int) {
- // 構建堆
- length := len(data)
- for i := (length - 2) / 2; i >= 0; i-- {
- heapify(data, length, i)
- }
- // 排序
- for length > 0 {
- length--
- data[length], data[0] = data[0], data[length]
- heapify(data, length, 0)
- }
- }
- func heapify(data []int, size, i int) {
- for {
- max := i
- if 2*i+1 < size && data[2*i+1] > data[max] {
- max = 2*i + 1
- }
- if 2*i+2 < size && data[2*i+2] > data[max] {
- max = 2*i + 2
- }
- if i == max {
- break
- }
- data[i], data[max] = data[max], data[i]
- i = max
- }
- }
相關復雜度如下:
| Time Complexity | |
|---|---|
| Best | O(nlog n) |
| Worst | O(nlog n) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | No |
歸并排序
歸并排序基于分治思想。
分治,顧名思義就是分而治之,它是一種解決問題的思路,將原始問題分解為多個相同或相似的子問題,然后將子問題解決,并將子問題的求得的解進行合并,這樣原問題就能夠得到解決了。
分治思想是很多復雜算法的基礎,例如歸并排序、快速排序、二分查找等等。
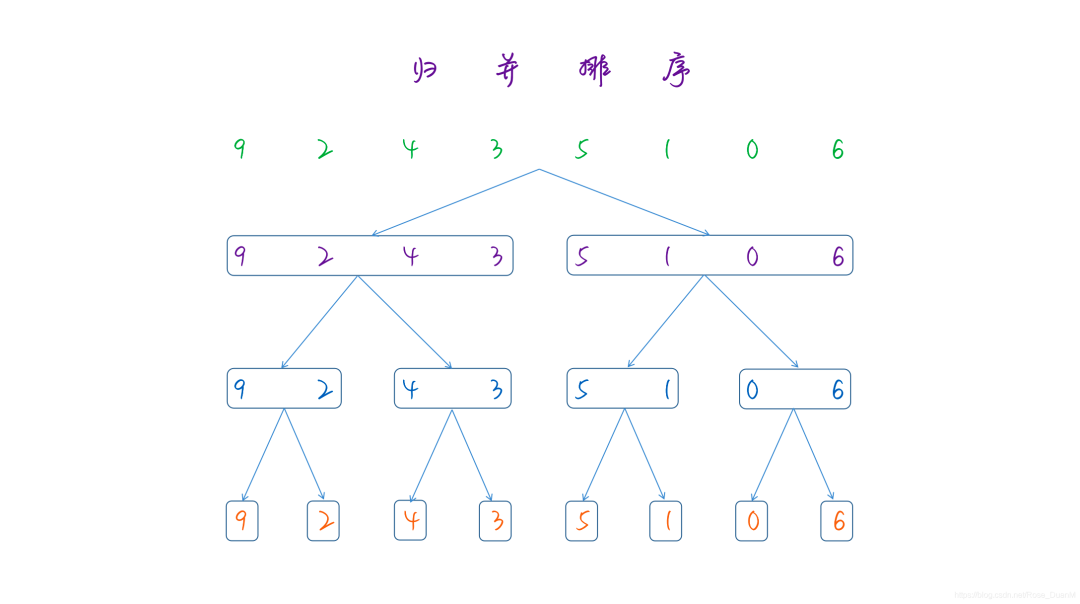
言歸正傳,再來看歸并排序,它的概念理解起來非常簡單,如果我們要對一組數據進行排序,我們可以將這個數組分為兩個子數組,子數組再進行分組,這樣子數組排序之后,將結果合并起來,就能夠得到原始數據排序的結果。
下面這張圖展示了將一個問題分解為多個子問題的過程:
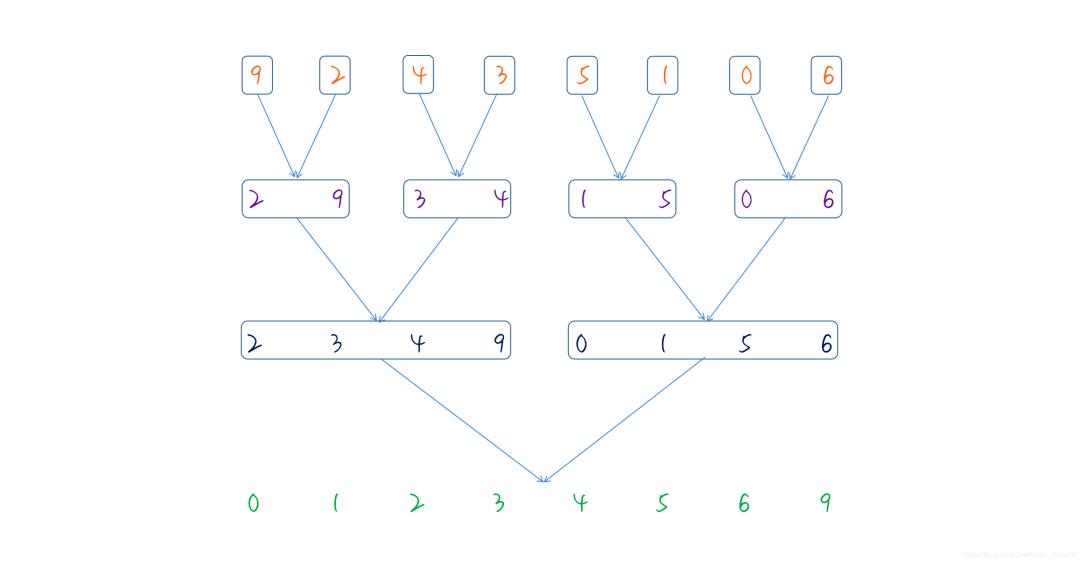
子問題得到解決之后,需要將結果合并,合并的過程如下圖:
代碼實現如下:
- //歸并排序
- func MergeSort(data []int) {
- mergeSortHelper(data, 0, len(data)-1)
- }
- func mergeSortHelper(data []int, lo, hi int) {
- if lo < hi {
- mid := lo + (hi-lo)/2
- mergeSortHelper(data, lo, mid)
- mergeSortHelper(data, mid+1, hi)
- merge(data, lo, mid, hi)
- }
- }
- func merge(data []int, lo, mid, hi int) {
- temp := make([]int, hi-lo+1)
- i, j, k := lo, mid+1, 0
- for i <= mid && j <= hi {
- if data[i] < data[j] {
- temp[k] = data[i]
- i++
- } else {
- temp[k] = data[j]
- j++
- }
- k++
- }
- copy(temp[k:], data[i:mid+1])
- copy(temp[k:], data[j:hi+1])
- copy(data[lo:hi+1], temp[:])
- }
相關復雜度如下:
| Time Complexity | |
|---|---|
| Best | O(n*log n) |
| Worst | O(n*log n) |
| Average | O(n*log n) |
| Space Complexity | O(n) |
| Stability | Yes |
3、快速排序
快速排序通常叫做“快排”,它應該是應用最廣泛的一個排序算法了,很多編程語言內置的排序方法,都或多或少使用到了快速排序,因為快速排序的時間復雜度可以達到 O(nlogn),并且是原地排序,前面介紹的幾種排序算法都無法將這兩個優點結合起來。
快排和歸并排序類似,都采用了分治思想,但是它的解決思路卻和歸并排序不太一樣。
如果要排序一個數組,我們可以從數組中選擇一個數據,做為分區點(pivot),然后將小于分區點的放到分區點的左側,大于分區點的放到其右側,然后對于分區點左右兩邊的數據,繼續采用這種分區的方式,直到數組完全有序。
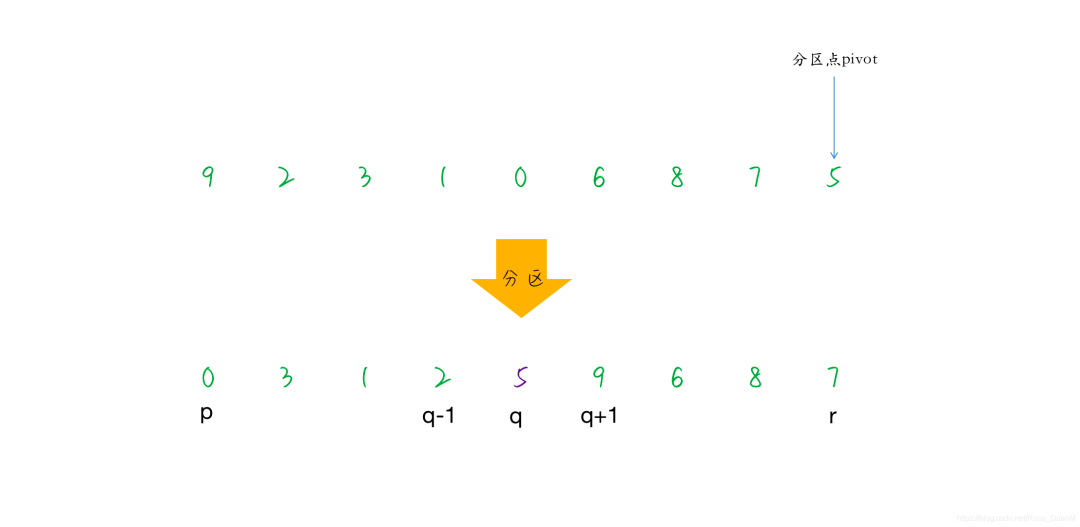
概念讀起來可能有點抽象,這里我畫了一張圖來幫助你理解整個排序的過程:
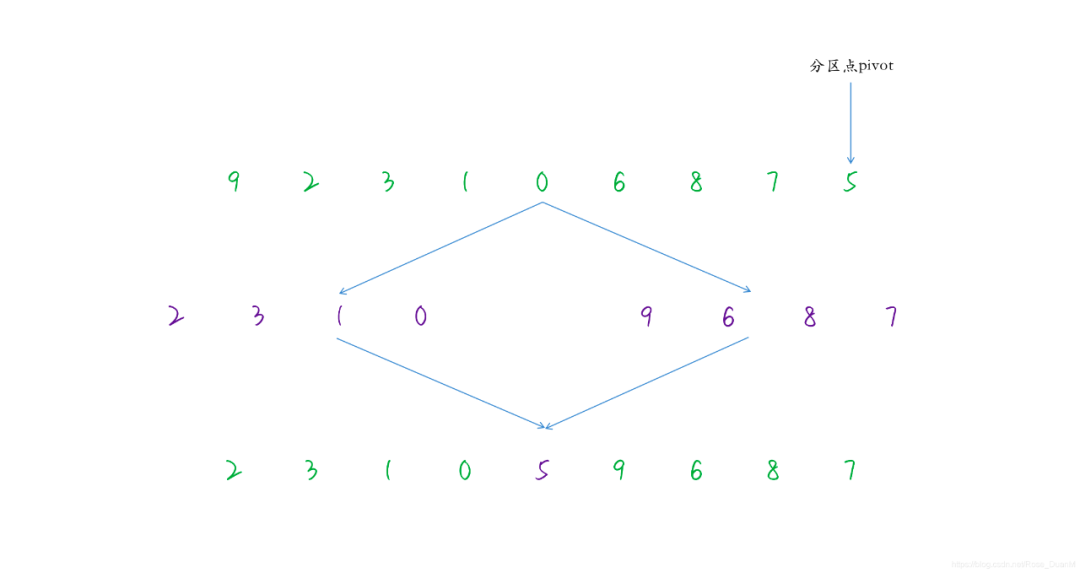
上圖展示了第一次分區的過程,假設要排序的數組的下標是 p ~ r,我們取數組的最后一個元素 5 做為分區點,然后比 5 小的數字 0 3 1 2 移動到 5 的左邊,比 5 大的數字 9 6 8 7 移動到 5 的右邊。
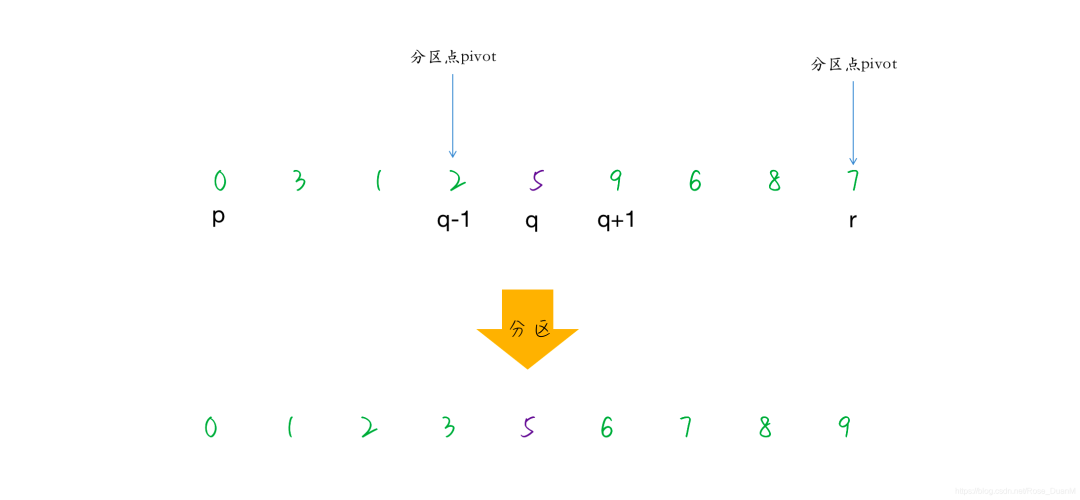
然后以數字 5 為分界點,其左邊的數字(下標為 p ~ q - 1),以及右邊的數字(下標為 q + 1 ~ r),分別再進行同樣的分區操作,一直分下去,直到數組完全有序,如下圖:
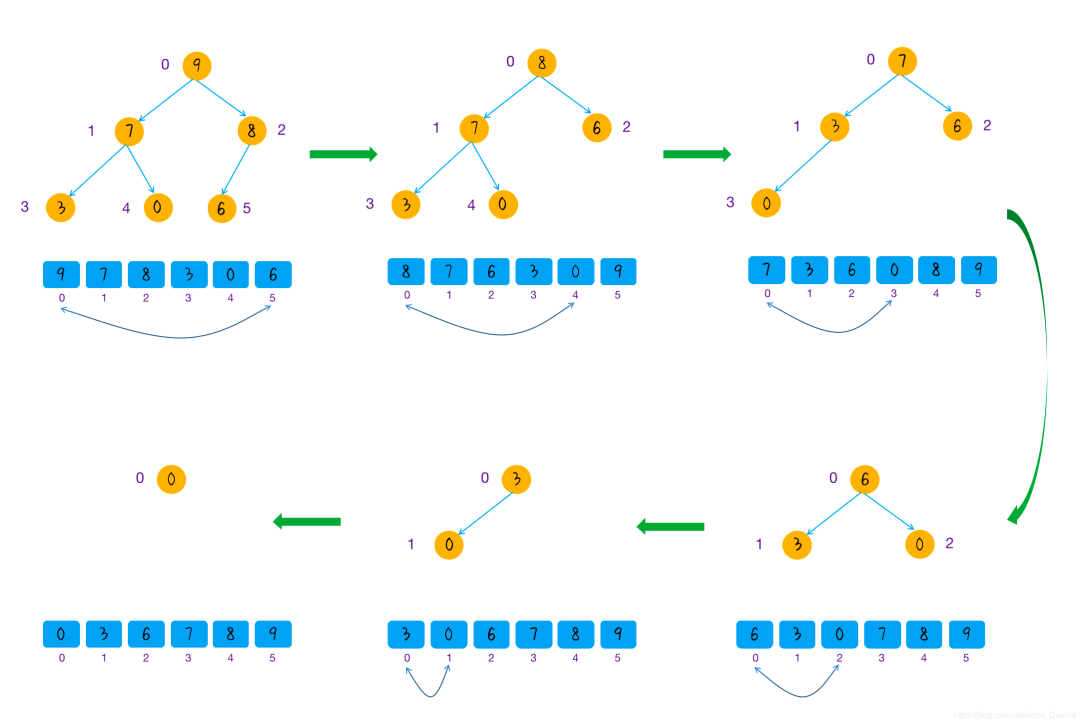
下面的動圖展示了快速排序的完整過程(注意動圖中是選擇第一個元素做為分區點的):
如果使用一個簡單的公式來表示快速排序,可以寫成這樣:
- int q = partition(data, p, r);
- quick_sort(data, p, r) = quick_sort(data, p, q - 1) + quick_sort(data, q + 1, r);
這里有一個 partition 分區函數,它的作用是選擇一個分區點,并且將小于分區點的數據放到其左邊,大于分區點的放到其右邊,然后返回分區點的下標。
其實這個 partition 分區函數是快速排序實現的關鍵,那究竟怎么實現這個函數呢?很容易想到的一種方式是:直接遍歷一次原數組,依次取出小于和大于分區點的數據,將其各自存放到一個臨時數組中,然后再依次拷貝回原數組中,過程如下圖:
這樣做雖然簡單,但是存在一個缺陷,那就是每次分區都會使用額外的存儲空間,這會導致快速排序的空間復雜度為 O(n),那么就不是原地排序了。
所以快速排序使用了另一種方式來實現分區,并且沒有借助額外的存儲空間,它是怎么實現的呢?我還是畫了一張圖來幫助你理解:
聲明了兩個指針 i 和 j,從數組的最開始處向后移動,這里的移動規則有兩個:
- 一是如果 j 所在元素大于分區點,那么 j 向后移動一位,i 不變;
- 二是如果 j 所在元素小于分區點,那么交換 i 和 j 所在元素,然后 i 和 將 j 同時向后移動一位。
終止的條件是 j 移動至數組末尾,然后交換分區點和 i 所在的元素,i 就是分區點的下標。
理解了這個過程之后,再來看快速排序的代碼實現,就會非常的簡單了,下面是一個示例:
- func QuickSort(data []int) {
- quickSortHelper(data, 0, len(data)-1)
- }
- func quickSortHelper(data []int, lo, hi int) {
- if lo < hi {
- mid := partition(data, lo, hi)
- quickSortHelper(data, lo, mid-1)
- quickSortHelper(data, mid+1, hi)
- }
- }
- func partition(data []int, lo, hi int) int {
- pivot, i, j := data[hi], lo, lo
- for j < hi {
- if data[j] < pivot {
- data[j], data[i] = data[i], data[j]
- i++
- }
- j++
- }
- data[i], data[hi] = data[hi], data[i]
- return i
- }
快速排序相關復雜度如下:
| Time Complexity | |
|---|---|
| Best | O(n*log n) |
| Worst | O(n2) |
| Average | O(n*log n) |
| Space Complexity | O(log n) |
| Stability | No |
文中的全部代碼可在我的 Github 上查看:https://github.com/roseduan/Go-Algorithm