重溫三十年前對于 NN 的批判:神經網絡無法實現可解釋 AI
1 可解釋AI (XAI)
隨著深度神經網絡 (DNN) 用于決定貸款批準、工作申請、批準法院保釋等與人們利益息息相關或者一些生死攸關的決定(例如在高速公路上突然停車),去解釋這些決定,而不僅僅是產生一個預測分數,是至關重要的。
可解釋人工智能 (XAI) 的研究最近集中在反事實(counterfactual)例子的概念上。這個想法很簡單:首先制造一些有預期輸出的反事實樣例并輸入到原來的網絡中;然后,讀取隱層單元解釋為什么網絡會產生一些其他輸出。更正式地說:
“返回分數 p 是因為變量 V 具有與其關聯的值 (v1, v2, ...)。如果 V 具有值 (v′1 , v′2 , ...),并且所有其他變量保持不變, 分數 p' 會被返回。”
下面則是更加具體的一個例子:
“你被拒絕貸款是因為你的年收入是 30,000 英鎊。如果你的收入是 45,000 英鎊,你就會獲得貸款。”
然而,一篇由Browne 和 Swift提出的論文[1] (以下簡稱 B&W)最近表明,反事實示例只是稍微更有意義的對抗性示例,這些示例是通過對輸入執行小的且不可觀察的擾動而產生的,從而導致網絡對它們進行錯誤分類具有很高的自信度。
此外,反事實的例子「解釋」了一些特征應該是什么才能得到正確的預測,但「沒有打開黑匣子」;也就是說,沒有解釋算法是如何工作的。文章繼續爭辯說,反事實的例子并沒有為可解釋性提供解決方案,并且「沒有語義就沒有解釋」。
事實上,文章甚至提出了更強有力的建議:
1)我們要么找到一種方法來提取假定存在于網絡隱藏層中的語義,要么
2)承認我們失敗。
而Walid S. Saba本人則對(1)持悲觀態度,換句話說他遺憾地承認我們的失敗,以下是他的理由。
2 Fodor 和 Pylyshyn 的「鬼魂」
雖然大眾完全同意B&W的觀點,即“沒有語義就沒有解釋”,但解釋深度神經網絡中隱藏層表示的語義為深度學習系統產生令人滿意的解釋的希望之所以不能夠實現,作者認為,原因正是出自三十多年前Fodor 和 Pylyshyn [2]中概述的原因。
Walid S. Saba接著論證到:在解釋問題出在哪里之前,我們需要注意到,純粹的外延模型(例如神經網絡)不能對系統性(systematicity)和組合性(compositionality)進行建模,因為它們不承認具有可再衍生的句法和相應語義的符號結構。
因此,神經網絡中的表示并不是真正與任何可解釋的事物相對應的“符號”——而是分布的、相關的和連續的數值,它們本身并不意味著任何可以在概念上解釋的東西。
用更簡單的術語來說,神經網絡中的子符號表示本身并不指代人類在概念上可以理解的任何事物(隱藏單元本身不能代表任何形而上學意義的對象)。相反,它是一組隱藏單元,它們通常共同代表一些顯著特征(例如,貓的胡須)。
但這正是神經網絡無法實現可解釋性的原因,即因為幾個隱藏特征的組合是不可確定的——一旦組合完成(通過一些線性組合函數),單個單元就會丟失(我們將在下面展示)。
3 可解釋性是“反向推理”,DNN無法逆向推理
作者討論過為什么 Fodor 和 Pylyshyn 得出的結論是 NN 不能對系統性(因此是可解釋的)推論進行建模[2]。
在符號系統中,有定義明確的組合語義函數,它們根據成分的意義計算復合詞的意義。但是這種組合是可逆的——
也就是說,人們總是可以得到產生該輸出的(輸入)組件,并且正是因為在符號系統中,人們可以訪問一種“句法結構”,這一結構含有如何組裝組件的地圖。而這在 NN 中都并非如此。一旦向量(張量)在 NN 中組合,它們的分解就無法確定(向量(包括標量)可以分解的方式是無限的!)
為了說明為什么這是問題的核心,讓我們考慮一下 B&W 提出的在 DNN 中提取語義以實現可解釋性的建議。B&W 的建議是遵循以下原則:
輸入圖像被標記為“建筑”,因為通常激活輪轂蓋的隱藏神經元 41435 的激活值為 0.32。如果隱藏神經元 41435 的激活值為 0.87,則輸入圖像將被標記為“汽車”。
要了解為什么這不會導致可解釋性,只需注意要求神經元 41435 的激活為 0.87 是不夠的。為簡單起見,假設神經元 41435 只有兩個輸入,x1 和 x2。我們現在所擁有的如下圖 1 所示:
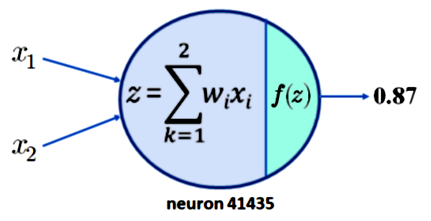
圖注:擁有兩個輸入的單一神經元的輸出為0.87
現在假設我們的激活函數 f 是流行的 ReLU 函數,那么可以產生 z = 0.87 的輸出。這意味著對于下表中顯示的 x1、x2、w1 和 w2 的值,可以得到 0.87 的輸出。
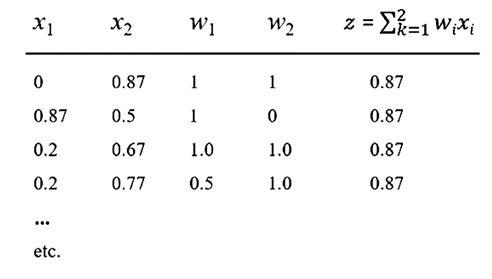
表注:多種輸入方式都可以產生0.87的數值
查看上表,很容易看出 x1、x2、w1 和 w2 的線性組合有無數個,它們會產生輸出 0.87。這里的重點是 NN 中的組合性是不可逆的,因此無法從任何神經元或任何神經元集合中捕獲有意義的語義。
為了與 B&W 的口號“沒有語義就沒有解釋”保持一致,我們聲明永遠無法從 NN 獲得任何解釋。簡而言之,沒有組合性就沒有語義,沒有語義就沒有解釋,DNN 無法對組合性進行建模。這可以形式化如下:
1. 沒有語義就沒有解釋[1] 2. 沒有可逆的組合性就沒有語義[2]
3. DNN 中的組合性是不可逆的[2]
=> DNN 無法解釋(沒有 XAI)
結束。
順便說一句,DNN 中的組合性是不可逆的這一事實除了無法產生可解釋的預測之外還有其他后果,尤其是在需要更高層次推理的領域,如自然語言理解 (NLU)。
特別是,這樣的系統確實無法解釋一個孩子如何僅從 (<human> <likes> <entity>) 之類的模板中學習如何解釋無限數量的句子,因為“約翰”、“鄰居女孩”、 “總是穿著T恤來這里的男孩”等都是<human>的可能實例化,還有“經典搖滾”、“成名”、“瑪麗的奶奶”、“在海灘上跑步”、 等都是 <entity> 的所有可能的實例。
因為這樣的系統沒有“記憶”,而且它們的組成不能顛倒,理論上它們需要無數個例子來學習這個簡單的結構。【編者注:這一點正好是喬姆斯基對于結構主義語言學的質疑,并由此開啟了影響語言學半個多世紀的轉化生成語法。】
最后,作者強調,三十多年前Fodor 和 Pylyshyn [2]提出了對 NN 作為認知架構的批評——他們展示了為什么 NN 不能對系統性、生產力和組合性進行建模,所有這些都是談論任何“語義”所必須的——而這一令人信服的批評從未得到完美的回答。
隨著解決人工智能可解釋性問題的需求變得至關重要,我們必須重新審視那篇經典論文,因為它顯示了將統計模式識別等同于人工智能進步的局限性。