相互作用的電子在不同能量和溫度下表現出多樣的獨特現象，假如我們對其周圍環境進行改變，它們又會出現新的集體行為，例如自旋、配對波動等，然而處理電子之間的這些現象還存在很多困難。很多研究者使用重整化群（Renormalization Group, RG）來解決。

在高維數據背景下，機器學習 (ML) 技術和數據驅動方法的出現在量子物理中引發了研究者巨大的興趣，到目前為止，ML 思想已被用于電子系統的相互作用。

本文中，來自博洛尼亞大學等機構的物理學家利用人工智能，將一個迄今為止需要 10 萬個方程的量子問題，壓縮為一個只需 4 個方程的小任務，而所有這些都在不犧牲準確率的情況下完成，這項研究于近日發表在《物理評論快報》上。

論文地址：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402

該研究的第一作者、博洛尼亞大學助理教授 Domenico Di Sante 表示：我們將這個浩大的工程耦合在一起，之后使用機器學習濃縮成一個手指都能數得過來的任務。

這項研究涉及這一問題，即電子在網格狀晶格上運動時動作是怎樣的。根據已有的經驗，當兩個電子占據同一晶格點陣時，它們就會產生相互作用。這一現象可以稱為 Hubbard 模型，其是有些材料的理想化設置，基于此，科學家能夠了解電子行為如何產生物質相，例如超導性，電子在沒有阻力的情況下流過材料。在將新方法應用于更復雜的量子系統之前，該模型還可以作為新方法的試驗場。

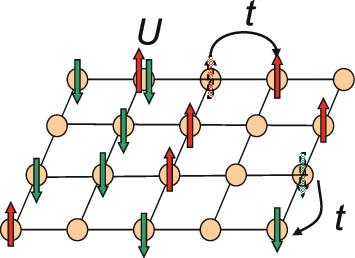
二維 Hubbard 模型示意圖

Hubbard 模型看似簡單，但即使是使用尖端計算方法處理少量的電子，也需要強大的算力。這是因為當電子相互作用時，電子之間就變成了量子力學糾纏問題：即使電子所處晶格的位置相距很遠，也不能單獨處理這兩個電子，所以物理學家必須同時處理所有電子，而不是每次只處理一個電子。電子越多，量子力學糾纏就會越多，計算難度就會成倍增加。

研究量子系統的一個常用方法是重整化群。作為一種數學裝置，物理學家用它來觀察一個系統的行為，比如可以用來觀察 Hubbard 模型。遺憾的是，一個重整化群記錄了電子之間所有可能的耦合，這些耦合可能包含成千上萬、數十萬甚至數百萬個需要求解的獨立方程。最重要的是，方程很復雜：每個方程都代表一對相互作用的電子。

Di Sante 團隊想知道他們是否可以使用一種稱為神經網絡的機器學習工具來使重整化群更易于管理。

就神經網絡而言，首先，研究者使用機器學習程序對全尺寸重整化群建立連接；然后神經網絡調整這些連接的強度，直到它找到一個小的方程集，生成與原始的、超大的重整化群相同的解。最后得出四個方程，即使只有四個，該程序的輸出也捕捉到了 Hubbard 模型的物理性質。

Di Sante 表示：「神經網絡本質上是一臺能夠發現隱藏模式的機器，這一結果超出了我們的預期。」

訓練機器學習程序需要大量的算力，因而他們花費了數周的時間才完成。好消息是，現在他們的程序已經開始投入使用，稍微調整就能解決其他問題，而無需從頭開始。

在談到之后的研究方向時，Di Sante 表示需要驗證新方法在更復雜的量子系統上的效果如何。此外，Di Sante 還表示，在關于重整化群的其他領域中使用該技術也有很大的可能性，例如宇宙學和神經科學。

論文概述

針對描述了正方形晶體上廣泛研究的二維 t-t' Hubbard 模型的功能重整化群（fRG）流特征的尺度相關四頂點函數，研究者執行了數據驅動降維。他們證明在低維潛在空間中基于神經常微分方程（NODE）求解器的一個深度學習架構能夠高效學習描述 Hubbard 模型各種磁性和 d-wave 超導狀態的 fRG 動力學。

研究者進一步提出了動態模式分解分析，它能夠確認少數模式確實足以捕獲 fRG 動力學。研究證明了使用人工智能提取相關電子四頂點函數的緊湊表示的可能性，這是成功實現尖端量子場理論方法并解決多電子問題的最重要目標。

fRG 中的基本對象是頂點函數 V（k_1, k_2, k_3），在原則上需要計算和存儲三個連續動量變量組成的一個函數。通過研究特定的理論模式，二維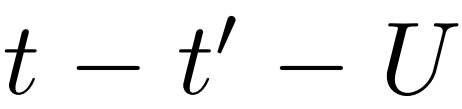  Hubbard 模型認為這與 cuprates 以及廣泛的有機導體相關。研究者表明，較低的維數表示可以捕獲高維頂點函數的 fRG 流。

Hubbard 模型的 fRG 接地狀態。研究者考慮的微觀哈密頓量（Hamiltonian）如下公式（1）所示。

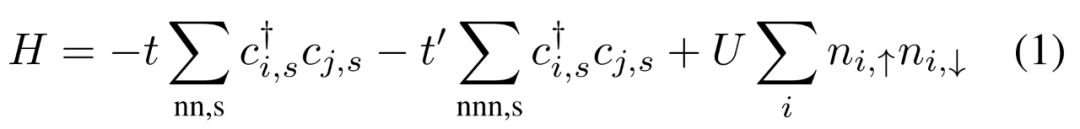
Hubbard 模型的 2 粒子特性通過溫度流的一環（one-loop）fRG 方案進行研究，其中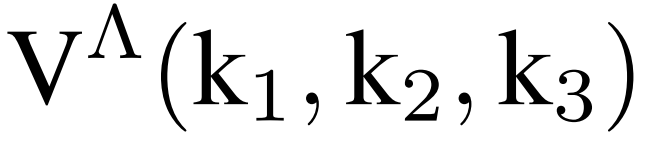的 RG 流如下公式（2）所示。

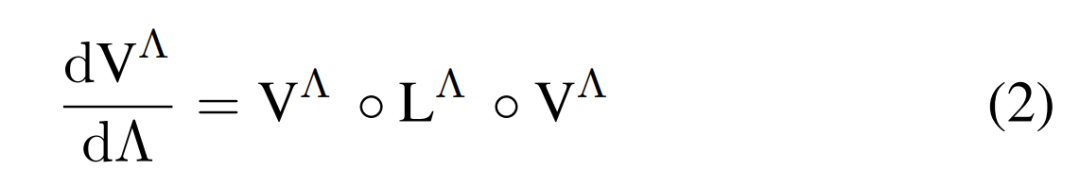
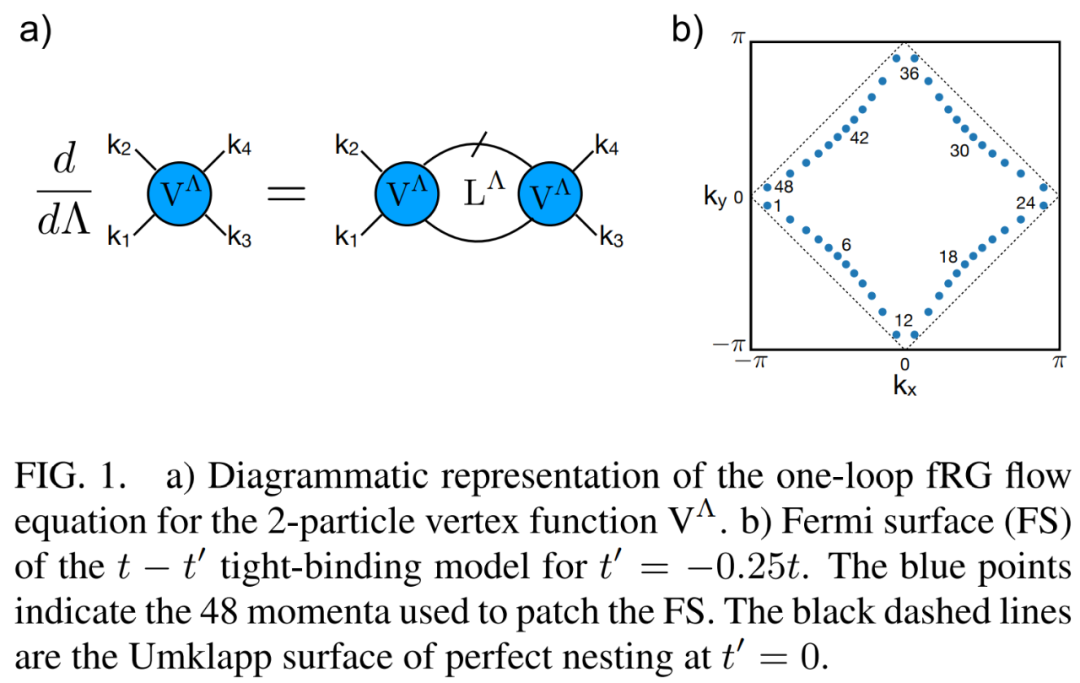
下圖 1 a)為 2 粒子頂點函數 V^Λ的一環 fRG 流方程圖解表示。

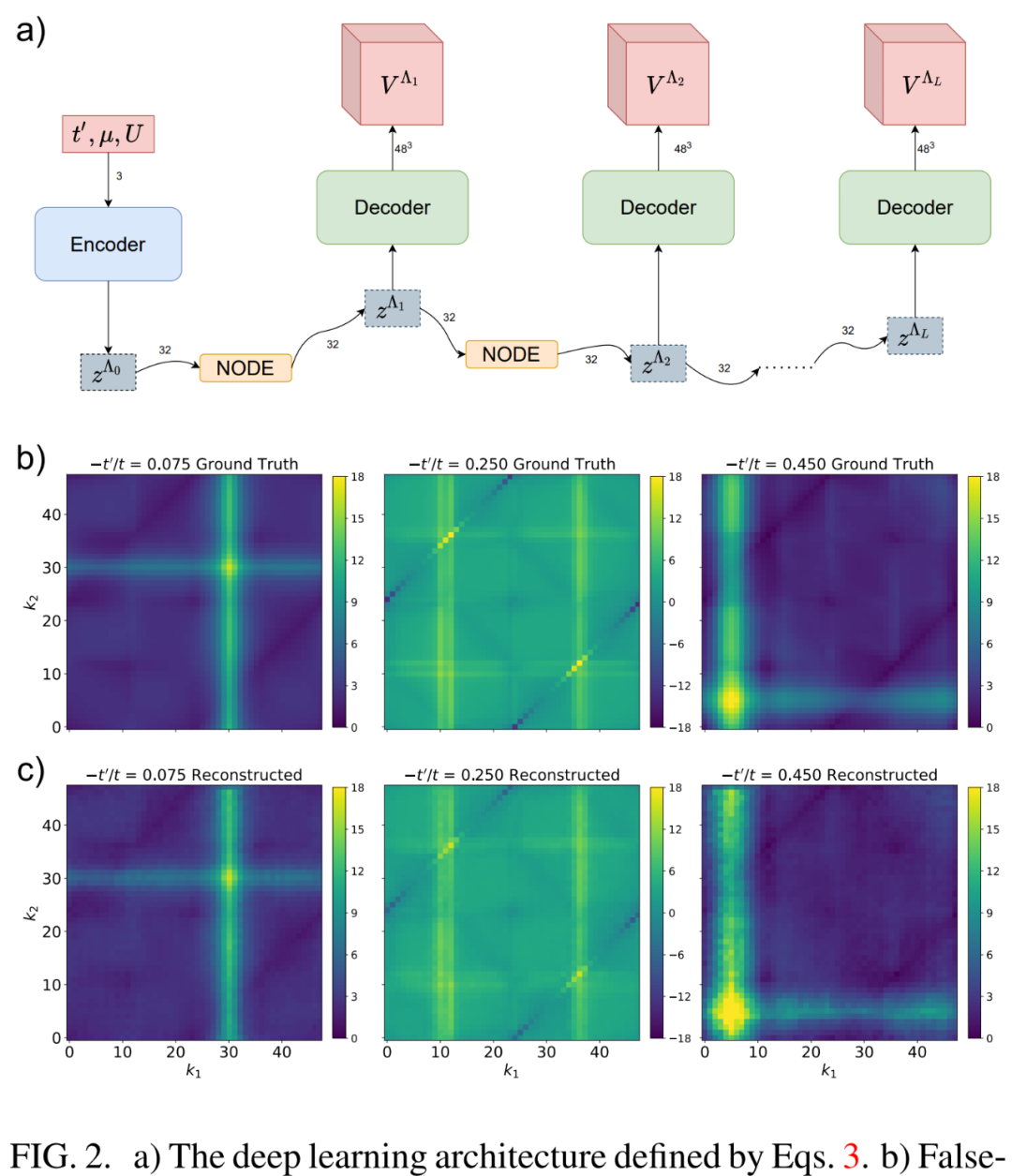
接下來看深度學習 fRG。如下圖 2 b)所示，通過在 fRG 流趨向強耦合以及一環近似分解之前檢查 2 粒子頂點函數的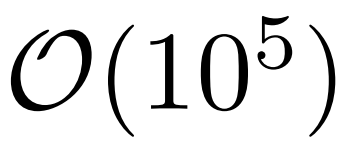耦合， 研究者認識到它們中的很多要么保持邊緣狀態要么在 RG 流下變得不相關。

研究者在基于適合當前高維問題的參數化 NODE 架構實現靈活的降維方案，該方法如下圖 2 a）所示，重點關注深度神經網絡。

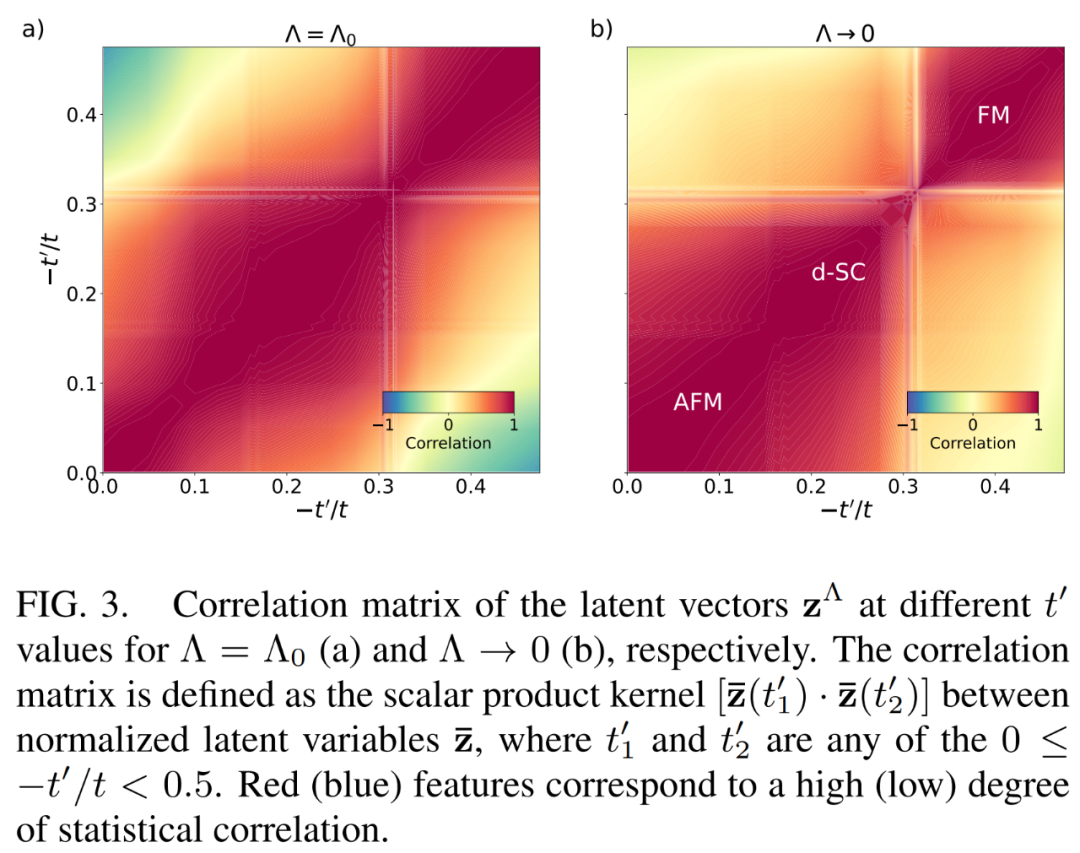
下圖 3 展示了在潛在空間的 fRG 動力學過程中，三個統計上高度相關的潛在空間表示 z 作為 NODE 神經網絡的學得特征。

更多細節內容請參閱原論文。