譯者 | 朱先忠

審校 | 孫淑娟

傳統(tǒng)的球面CNN無法擴展到高分辨率分類任務(wù)。在本文中，我們介紹了球面散射層（spherical scattering layers）——一種新型的球面層，它可以降低輸入數(shù)據(jù)的維數(shù)，同時保留相關(guān)信息，同時還具有旋轉(zhuǎn)等變的特性。

散射網(wǎng)絡(luò)通過使用小波分析中預(yù)定義的卷積濾波器進行工作，而不是從頭開始學(xué)習(xí)卷積濾波器。由于散射層的權(quán)重是專門設(shè)計的而不是通過學(xué)習(xí)得到的，因此散射層可以用作一次性預(yù)處理步驟，從而降低輸入數(shù)據(jù)的分辨率。我們以往的經(jīng)驗表明，配備初始散射層的球面CNN可以擴展到數(shù)千萬像素的分辨率，這一壯舉以前在傳統(tǒng)球面CNN層中是難以實現(xiàn)的。

傳統(tǒng)球面深度學(xué)習(xí)方法需要計算

球面CNN（文獻1，2，3）對于解決機器學(xué)習(xí)中的多種不同類型的問題都非常有用，因為這其中許多問題的數(shù)據(jù)源不能自然地在平面上表示（有關(guān)這方面的入門性介紹，請參閱我們的前一篇文章，地址是：https://towardsdatascience.com/geometric-deep-learning-for-spherical-data-55612742d05f）。

球面CNN的一個關(guān)鍵特性是，它們與球面數(shù)據(jù)的旋轉(zhuǎn)是等變的（在本文中，我們重點討論旋轉(zhuǎn)等變方法）。實際上，這意味著球面CNN具有令人印象深刻的泛化特性，允許它們執(zhí)行諸如分類3D對象網(wǎng)格之類的操作，而不管它們是如何旋轉(zhuǎn)的（以及它們在訓(xùn)練期間是否看到網(wǎng)格的不同旋轉(zhuǎn)）。

我們在最近發(fā)布的文章中描述了Kagenova團隊為提高球面CNN的計算效率而開發(fā)的一系列進展成果（參考地址：https://towardsdatascience.com/efficient-generalized-spherical-cnns-1493426362ca）。我們所采用的方法——高效的廣義球面CNN——既保留了傳統(tǒng)球面CNN的等方差特性，同時又使得計算效率更高（文獻1）。然而，盡管在計算效率方面取得了這些進步，球面CNN仍然局限于相對低分辨率的數(shù)據(jù)。這意味著，球面CNN目前還不能應(yīng)用于通常涉及更高分辨率數(shù)據(jù)的激動人心的應(yīng)用場景中，例如宇宙學(xué)數(shù)據(jù)分析和虛擬現(xiàn)實的360度計算機視覺等領(lǐng)域。在最近發(fā)布的一篇文章中，我們介紹了球面散射層網(wǎng)絡(luò)，以便靈活調(diào)整高效的通用球面CNN來提高分辨率（文獻4），在本文中我們將對該內(nèi)容進行一下回顧。

支持高分辨率輸入數(shù)據(jù)的混合方法

在開發(fā)高效的通用球面CNN（文獻1）時，我們發(fā)現(xiàn)了一種非常有效的構(gòu)建球面CNN架構(gòu)的混合方法。混合球面CNN可以在同一網(wǎng)絡(luò)中使用不同風(fēng)格的球面CNN層，允許開發(fā)人員在不同處理階段獲得不同類型層的好處。

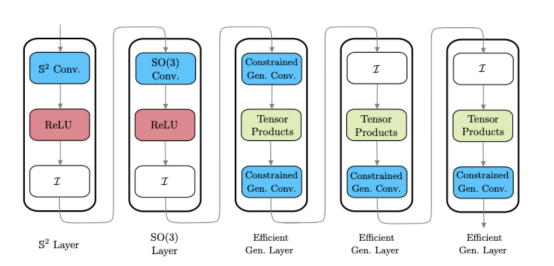
上圖展示了混合球面CNN架構(gòu)示例圖（請注意：這些層不是單一的，而是一些不同風(fēng)格的球面CNN層）。

球面上的散射網(wǎng)絡(luò)繼續(xù)采用這種混合方法，并引入了一種新的球面CNN層，可以插入現(xiàn)有的球面架構(gòu)中。為了將高效的通用球面CNN擴展到更高維度，這一新層需要具備如下特征：

1. 計算支持下的可擴展性
2. 將信息混合到低頻，以允許后續(xù)層以低分辨率運行
3. 旋轉(zhuǎn)等變
4. 提供穩(wěn)定和局部不變的表示（即提供有效的表示空間）

我們確定散射網(wǎng)絡(luò)層具有滿足所有上面列舉的這些特征的潛力。

球面上的散射網(wǎng)絡(luò)

由Mallat（文獻5）在歐幾里德環(huán)境中首次提出的散射網(wǎng)絡(luò)可以被視為具有固定卷積濾波器的CNN，這些濾波器是從小波分析中導(dǎo)出的。散射網(wǎng)絡(luò)已被證明對傳統(tǒng)（歐氏）計算機視覺非常有用，尤其是在數(shù)據(jù)有限的情況下——而在這種情況下學(xué)習(xí)卷積濾波器是比較困難的。接下來，我們簡要討論一下散射網(wǎng)絡(luò)層的內(nèi)部工作原理、它們?nèi)绾螡M足上一節(jié)中定義的要求以及如何開發(fā)它們用于球面數(shù)據(jù)分析。

散射層內(nèi)的數(shù)據(jù)處理由三個基本操作執(zhí)行。第一個構(gòu)建塊是固定小波卷積，它類似于歐氏CNN中使用的正常學(xué)習(xí)卷積。在小波卷積之后，散射網(wǎng)絡(luò)對結(jié)果表示應(yīng)用模數(shù)非線性方法。最后，散射利用了一個縮放函數(shù)，該函數(shù)執(zhí)行了一種局部平均算法，與普通CNN中的池化層有一些相似之處。重復(fù)應(yīng)用這三個構(gòu)建塊就會將輸入數(shù)據(jù)分散到計算樹中，并在不同的處理階段將結(jié)果表示（類似于CNN頻道）從樹中提取出來。這些操作的簡略示意圖如下所示。

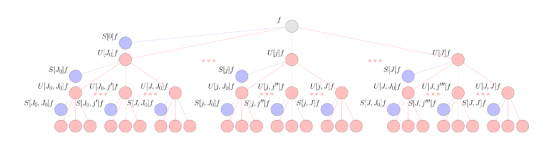
該圖示意了球面信號f的球面散射網(wǎng)絡(luò)。信號通過級聯(lián)球面小波變換傳播，并結(jié)合用紅色節(jié)點表示的絕對值激活函數(shù)。散射網(wǎng)絡(luò)的輸出是通過將這些信號投影到球面小波縮放函數(shù)上得到的，從而得到用藍色節(jié)點表示的散射系數(shù)。

從傳統(tǒng)的深度學(xué)習(xí)觀點來看，分散網(wǎng)絡(luò)的操作似乎有些模糊。然而，所描述的每種計算操作都有一個特定的目的——旨在利用小波分析的可靠的理論結(jié)果。

散射網(wǎng)絡(luò)中的小波卷積是經(jīng)過仔細推導(dǎo)的，以便從輸入數(shù)據(jù)中提取相關(guān)信息。例如，對于自然圖像，小波被定義為專門提取與高頻的邊緣和低頻的物體普通形狀相關(guān)的信息。因此，在平面設(shè)置中，散射網(wǎng)絡(luò)濾波器可能與傳統(tǒng)的CNN濾波器有一些相似之處。這同樣適用于球面設(shè)置，我們使用尺度離散小波（scale-discretised wavelets，詳見文獻4）。

由于小波濾波器是固定的，初始散射層只需要應(yīng)用一次，而不需要在整個訓(xùn)練過程中重復(fù)應(yīng)用（如傳統(tǒng)CNN中的初始層）。這使得散射網(wǎng)絡(luò)在計算上具有可擴展性，滿足上面特征1的要求。此外，散射層降低了其輸入數(shù)據(jù)的維數(shù)，這意味著在訓(xùn)練下游CNN層時，只需要使用有限的存儲空間來緩存散射表示。

小波卷積后面采用的是模數(shù)非線性方法。首先，這給神經(jīng)網(wǎng)絡(luò)層注入了非線性特征。其次，模數(shù)運算將輸入信號中的高頻信息混合到低頻數(shù)據(jù)中，滿足上面的要求2。下圖顯示了模數(shù)非線性計算前后數(shù)據(jù)的小波表示的頻率分布情況。

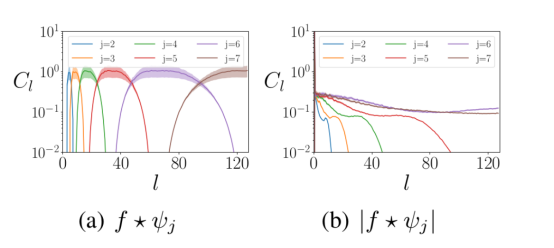
上圖展示了模運算前后不同球面頻率l處小波系數(shù)的分布。輸入信號中的能量從高頻（左側(cè)面板）移動到低頻（右側(cè)面板）。其中，f是輸入信號，Ψ代表縮放j的小波。

應(yīng)用模數(shù)計算后，將得到的信號投影到縮放函數(shù)上。縮放函數(shù)從表示結(jié)果中提取低頻信息，類似于傳統(tǒng)CNN中的池化函數(shù)操作。

我們對球面散射網(wǎng)絡(luò)的理論上的等方差特性進行了經(jīng)驗測試。測試是通過旋轉(zhuǎn)信號并將其通過散射網(wǎng)絡(luò)饋送，然后將得到的結(jié)果表示與輸入數(shù)據(jù)通過散射網(wǎng)絡(luò)后再進行旋轉(zhuǎn)計算的結(jié)果表示進行比較。由下表中的數(shù)據(jù)可以證明給定深度的等方差誤差較低，因此滿足上述要求3（通常在實踐中，一個路徑深度不會超過兩個路徑的深度，因為大多數(shù)信號能量已經(jīng)被捕獲）。

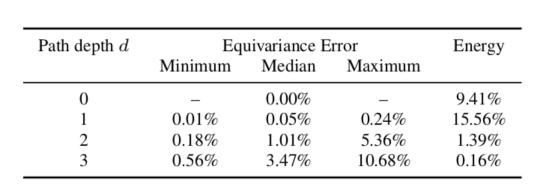
不同深度球面散射網(wǎng)絡(luò)的旋轉(zhuǎn)等方差誤差

最后，從理論上證明了歐氏散射網(wǎng)絡(luò)對小的微分或畸變是穩(wěn)定的（文獻5）。目前，這個結(jié)果已經(jīng)推廣到緊致黎曼流形上的散射網(wǎng)絡(luò)（文獻6），特別是球面環(huán)境（文獻4）。在實踐中，對差異形態(tài)的穩(wěn)定性意味著，如果對輸入進行輕微更改，散射網(wǎng)絡(luò)計算的表示不會有顯著差異（關(guān)于穩(wěn)定性在幾何深度學(xué)習(xí)中的作用的討論，請參閱我們之前的帖子，地址是https://towardsdatascience.com/a-brief-introduction-to-geometric-deep-learning-dae114923ddb）。因此，散射網(wǎng)絡(luò)提供了一個表現(xiàn)良好的表示空間，在該空間上可以有效地進行隨后的學(xué)習(xí)，滿足上述第4項要求。

可縮放和旋轉(zhuǎn)等變的球面CNN

考慮到引入的散射層滿足我們所有想要的特性，接下來我們準備將它們集成到我們的混合球面CNN中。如前所述，散射層可以作為初始預(yù)處理步驟固定到現(xiàn)有架構(gòu)上，以減小后續(xù)球面層處理的表示的大小。

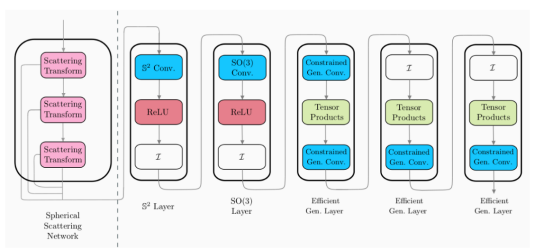
在上圖中，散射層模塊（虛線左側(cè)）是一個設(shè)計層。這意味著，它不需要訓(xùn)練，而其余層（虛線右側(cè)）是可訓(xùn)練的。因此，這意味著散射層可以作為一次性預(yù)處理步驟應(yīng)用，以降低輸入數(shù)據(jù)的維數(shù)。

由于散射網(wǎng)絡(luò)具有給定輸入的固定表示，因此散射網(wǎng)絡(luò)層可以在訓(xùn)練開始時應(yīng)用于整個數(shù)據(jù)集一次，并緩存生成的低維表示以訓(xùn)練后續(xù)層。幸運的是，散射表示具有降低的維度，這意味著存儲它們所需的磁盤空間相對較低。由于存在這個新的球面散射層，所以可以把高效的廣義球面CNN擴展到高分辨率分類問題領(lǐng)域。

宇宙微波背景各向異性的分類

物質(zhì)在整個宇宙中是如何分布的？這是宇宙學(xué)家的一個基本研究問題，對我們宇宙的起源和演化的理論模型具有重大意義。宇宙微波背景輻射（CMB）——來自大爆炸的殘余能量——描繪了宇宙中物質(zhì)的分布。宇宙學(xué)家在天球上觀察CMB，這需要能夠在天球內(nèi)進行宇宙學(xué)分析的計算方法。

宇宙學(xué)家對分析宇宙微波背景的方法非常感興趣，因為這些方法能夠檢測宇宙微波背景在整個空間的分布中的非高斯性，這對早期宇宙理論具有重要意義。這種分析方法還需要能夠擴展到天文分辨率。我們通過將CMB模擬分為高斯或非高斯，分辨率為L=1024，證明了我們的散射網(wǎng)絡(luò)能夠滿足這些要求。散射網(wǎng)絡(luò)成功地將這些模擬分類，準確度為95.3%，比低分辨率傳統(tǒng)球面CNN的53.1%要好得多。

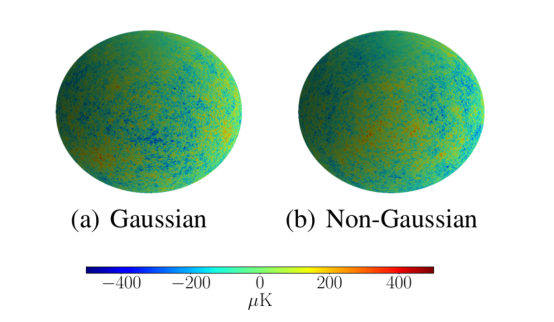
上圖給出高斯和非高斯類CMB的高分辨率模擬示例，用于評估球面散射網(wǎng)絡(luò)擴展到高分辨率的能力。

總結(jié)

在本文中，我們探討了球面散射層能夠壓縮其輸入表示的維度，同時還保留下游任務(wù)的重要信息。我們已經(jīng)證明，這使得散射層對于高分辨率的球面分類任務(wù)非常有用。這為以前難以解決的例如宇宙學(xué)數(shù)據(jù)分析和高分辨率360圖像/視頻分類等潛在應(yīng)用打開了大門。然而，許多例如分割或深度估計這樣的需要密集預(yù)測的計算機視覺問題都需要高維輸出和高維輸入。最后，如何開發(fā)可控制的既可以增加輸出表示維度同時又能夠保持等方差的球面CNN層，這是Kagenova開發(fā)人員當前研究的主題。這些內(nèi)容將在下一篇文章中進行介紹。

參考文獻

［1］Cobb, Wallis, Mavor-Parker, Marignier, Price, d’Avezac, McEwen, Efficient Generalised Spherical CNNs, ICLR (2021), arXiv:2010.11661

［2］ Cohen, Geiger, Koehler, Welling, Spherical CNNs, ICLR (2018), arXiv:1801.10130

［3］ Esteves, Allen-Blanchette, Makadia, Daniilidis, Learning SO(3) Equivariant Representations with Spherical CNNs, ECCV (2018), arXiv:1711.06721

［4］ McEwen, Jason, Wallis, Christopher and Mavor-Parker, Augustine N., Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs, ICLR (2022), arXiv:2102.02828

［5］ Bruna, Joan, and Stéphane Mallat, Invariant scattering convolution networks, IEEE Transaction on Pattern Analysis and Machine Intelligence (2013)

［6］ Perlmutter, Michael, et al., Geometric wavelet scattering networks on compact Riemannian manifolds, Mathematical and Scientific Machine Learning. PMLR (2020), arXiv:1905.10448

譯者介紹

朱先忠，51CTO社區(qū)編輯，51CTO專家博客、講師，濰坊一所高校計算機教師，自由編程界老兵一枚。

原文標題：??Scaling Spherical Deep Learning to High-Resolution Input Data??，作者：Jason McEwen，Augustine Mavor-Parker