本文將比較各種降維技術(shù)在機(jī)器學(xué)習(xí)任務(wù)中對(duì)表格數(shù)據(jù)的有效性。我們將降維方法應(yīng)用于數(shù)據(jù)集，并通過回歸和分類分析評(píng)估其有效性。我們將降維方法應(yīng)用于從與不同領(lǐng)域相關(guān)的 UCI 中獲取的各種數(shù)據(jù)集。總共選擇了 15 個(gè)數(shù)據(jù)集，其中 7 個(gè)將用于回歸，8 個(gè)用于分類。

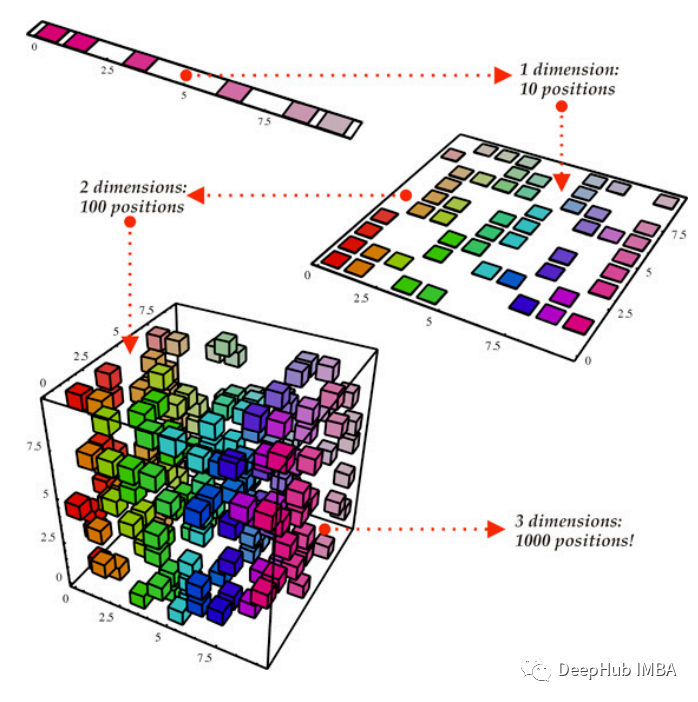
為了使本文易于閱讀和理解，僅顯示了一個(gè)數(shù)據(jù)集的預(yù)處理和分析。實(shí)驗(yàn)從加載數(shù)據(jù)集開始。數(shù)據(jù)集被分成訓(xùn)練集和測(cè)試集，然后在均值為 0 且標(biāo)準(zhǔn)差為 1 的情況下進(jìn)行標(biāo)準(zhǔn)化。

然后會(huì)將降維技術(shù)應(yīng)用于訓(xùn)練數(shù)據(jù)，并使用相同的參數(shù)對(duì)測(cè)試集進(jìn)行變換以進(jìn)行降維。對(duì)于回歸，使用主成分分析（PCA）和奇異值分解（SVD）進(jìn)行降維，另一方面對(duì)于分類，使用線性判別分析（LDA）

降維后就訓(xùn)練多個(gè)機(jī)器學(xué)習(xí)模型進(jìn)行測(cè)試，并比較了不同模型在通過不同降維方法獲得的不同數(shù)據(jù)集上的性能。

讓我們通過加載第一個(gè)數(shù)據(jù)集開始這個(gè)過程，

import pandas as pd ## for data manipulation
df = pd.read_excel(r'Regression\AirQualityUCI.xlsx')
print(df.shape)
df.head()

數(shù)據(jù)集包含15個(gè)列，其中一個(gè)是需要預(yù)測(cè)標(biāo)簽。在繼續(xù)降維之前，日期和時(shí)間列也會(huì)被刪除。

X = df.drop(['CO(GT)', 'Date', 'Time'], axis=1)
y = df['CO(GT)']
X.shape, y.shape

#Output: ((9357, 12), (9357,))

為了訓(xùn)練，我們需要將數(shù)據(jù)集劃分為訓(xùn)練集和測(cè)試集，這樣可以評(píng)估降維方法和在降維特征空間上訓(xùn)練的機(jī)器學(xué)習(xí)模型的有效性。模型將使用訓(xùn)練集進(jìn)行訓(xùn)練，性能將使用測(cè)試集進(jìn)行評(píng)估。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape

#Output: ((7485, 12), (1872, 12), (7485,), (1872,))

在對(duì)數(shù)據(jù)集使用降維技術(shù)之前，可以對(duì)輸入數(shù)據(jù)進(jìn)行縮放，這樣可以保證所有特征處于相同的比例上。這對(duì)于線性模型來說是是至關(guān)重要的，因?yàn)槟承┙稻S方法可以根據(jù)數(shù)據(jù)是否標(biāo)準(zhǔn)化以及對(duì)特征的大小敏感而改變其輸出。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
X_train.shape, X_test.shape

主成分分析(PCA)

線性降維的PCA方法降低了數(shù)據(jù)的維數(shù)，同時(shí)保留了盡可能多的數(shù)據(jù)方差。

這里將使用Python sklearn.decomposition模塊的PCA方法。要保留的組件數(shù)量是通過這個(gè)參數(shù)指定的，這個(gè)數(shù)字會(huì)影響在較小的特征空間中包含多少維度。作為一種替代方法，我們可以設(shè)定要保留的目標(biāo)方差，它根據(jù)捕獲的數(shù)據(jù)中的方差量建立組件的數(shù)量，我們這里設(shè)置為0.95

from sklearn.decomposition import PCA
pca = PCA(n_compnotallow=0.95)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)
X_train_pca

上述特征代表什么?主成分分析(PCA)將數(shù)據(jù)投射到低維空間，試圖盡可能多地保留數(shù)據(jù)中的不同之處。雖然這可能有助于特定的操作，但也可能使數(shù)據(jù)更難以理解。，PCA可以識(shí)別數(shù)據(jù)中的新軸，這些軸是初始特征的線性融合。

奇異值分解(SVD)

SVD是一種線性降維技術(shù)，它將數(shù)據(jù)方差較小的特征投影到低維空間。我們需要設(shè)置降維后要保留的組件數(shù)量。這里我們將把維度降低 2/3。

from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_compnotallow=int(X_train.shape[1]*0.33))
X_train_svd = svd.fit_transform(X_train)
X_test_svd = svd.transform(X_test)
X_train_svd

訓(xùn)練回歸模型

現(xiàn)在，我們將開始使用上述三種數(shù)據(jù)(原始數(shù)據(jù)集、PCA和SVD)對(duì)模型進(jìn)行訓(xùn)練和測(cè)試，并且我們使用多個(gè)模型進(jìn)行對(duì)比。

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVR
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.metrics import r2_score, mean_squared_error
import time

train_test_ML:這個(gè)函數(shù)將完成與模型的訓(xùn)練和測(cè)試相關(guān)的重復(fù)任務(wù)。通過計(jì)算rmse和r2_score來評(píng)估所有模型的性能。并返回包含所有詳細(xì)信息和計(jì)算值的數(shù)據(jù)集，還將記錄每個(gè)模型在各自的數(shù)據(jù)集上訓(xùn)練和測(cè)試所花費(fèi)的時(shí)間。

def train_test_ML(dataset, dataform, X_train, y_train, X_test, y_test):
  temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'R2 Score', 'RMSE', 'Time Taken'])
  for i in [LinearRegression, KNeighborsRegressor, SVR, DecisionTreeRegressor, RandomForestRegressor, GradientBoostingRegressor]:
      start_time = time.time()
      reg = i().fit(X_train, y_train)
      y_pred = reg.predict(X_test)
      r2 = np.round(r2_score(y_test, y_pred), 2)
      rmse = np.round(np.sqrt(mean_squared_error(y_test, y_pred)), 2)
      end_time = time.time()
      time_taken = np.round((end_time - start_time), 2)
      temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], r2, rmse, time_taken]
  return temp_df

原始數(shù)據(jù):

original_df = train_test_ML('AirQualityUCI', 'Original', X_train, y_train, X_test, y_test)
original_df

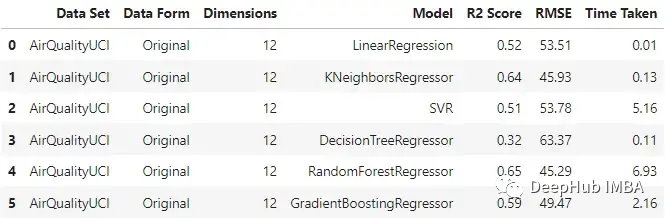
可以看到KNN回歸器和隨機(jī)森林在輸入原始數(shù)據(jù)時(shí)表現(xiàn)相對(duì)較好，隨機(jī)森林的訓(xùn)練時(shí)間是最長(zhǎng)的。

PCA

pca_df = train_test_ML('AirQualityUCI', 'PCA Reduced', X_train_pca, y_train, X_test_pca, y_test)
pca_df

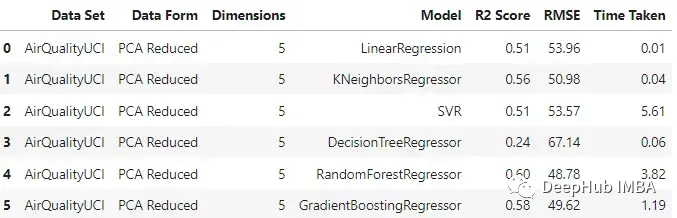
與原始數(shù)據(jù)集相比，不同模型的性能有不同程度的下降。梯度增強(qiáng)回歸和支持向量回歸在兩種情況下保持了一致性。這里一個(gè)主要的差異也是預(yù)期的是模型訓(xùn)練所花費(fèi)的時(shí)間。與其他模型不同的是，SVR在這兩種情況下花費(fèi)的時(shí)間差不多。

SVD

svd_df = train_test_ML('AirQualityUCI', 'SVD Reduced', X_train_svd, y_train, X_test_svd, y_test)
svd_df

與PCA相比，SVD以更大的比例降低了維度，隨機(jī)森林和梯度增強(qiáng)回歸器的表現(xiàn)相對(duì)優(yōu)于其他模型。

回歸模型分析

對(duì)于這個(gè)數(shù)據(jù)集，使用主成分分析時(shí)，數(shù)據(jù)維數(shù)從12維降至5維，使用奇異值分析時(shí)，數(shù)據(jù)降至3維。

• 就機(jī)器學(xué)習(xí)性能而言，數(shù)據(jù)集的原始形式相對(duì)更好。造成這種情況的一個(gè)潛在原因可能是，當(dāng)我們使用這種技術(shù)降低維數(shù)時(shí)，在這個(gè)過程中會(huì)發(fā)生信息損失。
• 但是線性回歸、支持向量回歸和梯度增強(qiáng)回歸在原始和PCA案例中的表現(xiàn)是一致的。
• 在我們通過SVD得到的數(shù)據(jù)上，所有模型的性能都下降了。
• 在降維情況下，由于特征變量的維數(shù)較低，模型所花費(fèi)的時(shí)間減少了。

將類似的過程應(yīng)用于其他六個(gè)數(shù)據(jù)集進(jìn)行測(cè)試，得到以下結(jié)果:

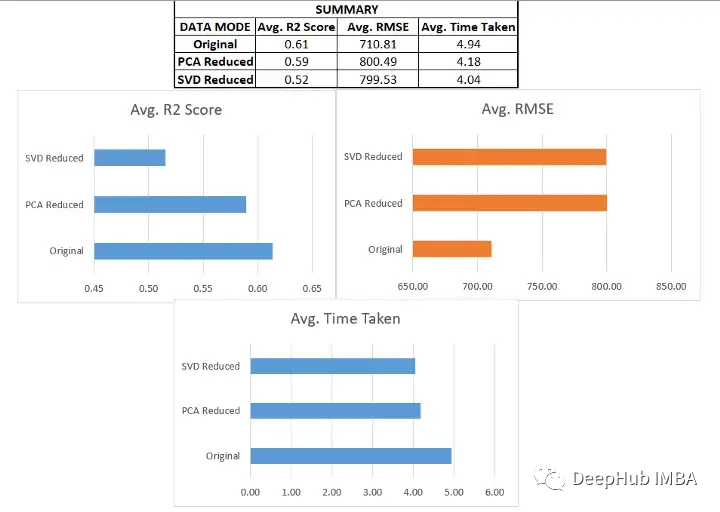
我們?cè)诟鞣N數(shù)據(jù)集上使用了SVD和PCA，并對(duì)比了在原始高維特征空間上訓(xùn)練的回歸模型與在約簡(jiǎn)特征空間上訓(xùn)練的模型的有效性

• 原始數(shù)據(jù)集始終優(yōu)于由降維方法創(chuàng)建的低維數(shù)據(jù)。這說明在降維過程中可能丟失了一些信息。
• 當(dāng)用于更大的數(shù)據(jù)集時(shí)，降維方法有助于顯著減少數(shù)據(jù)集中的特征數(shù)量，從而提高機(jī)器學(xué)習(xí)模型的有效性。對(duì)于較小的數(shù)據(jù)集，改影響并不顯著。
• 模型的性能在original和pca_reduced兩種模式下保持一致。如果一個(gè)模型在原始數(shù)據(jù)集上表現(xiàn)得更好，那么它在PCA模式下也會(huì)表現(xiàn)得更好。同樣，較差的模型也沒有得到改進(jìn)。
• 在SVD的情況下，模型的性能下降比較明顯。這可能是n_components數(shù)量選擇的問題，因?yàn)樘?shù)量肯定會(huì)丟失數(shù)據(jù)。
• 決策樹在SVD數(shù)據(jù)集時(shí)一直是非常差的，因?yàn)樗緛砭褪且粋€(gè)弱學(xué)習(xí)器

訓(xùn)練分類模型

對(duì)于分類我們將使用另一種降維方法：LDA。機(jī)器學(xué)習(xí)和模式識(shí)別任務(wù)經(jīng)常使用被稱為線性判別分析(LDA)的降維方法。這種監(jiān)督學(xué)習(xí)技術(shù)旨在最大化幾個(gè)類或類別之間的距離，同時(shí)將數(shù)據(jù)投影到低維空間。由于它的作用是最大化類之間的差異，因此只能用于分類任務(wù)。

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score, f1_score, recall_score, precision_score

繼續(xù)我們的訓(xùn)練方法

def train_test_ML2(dataset, dataform, X_train, y_train, X_test, y_test):
  temp_df = pd.DataFrame(columns=['Data Set', 'Data Form', 'Dimensions', 'Model', 'Accuracy', 'F1 Score', 'Recall', 'Precision', 'Time Taken'])
  for i in [LogisticRegression, KNeighborsClassifier, SVC, DecisionTreeClassifier, RandomForestClassifier, GradientBoostingClassifier]:
      start_time = time.time()
      reg = i().fit(X_train, y_train)
      y_pred = reg.predict(X_test)
      accuracy = np.round(accuracy_score(y_test, y_pred), 2)
      f1 = np.round(f1_score(y_test, y_pred, average='weighted'), 2)
      recall = np.round(recall_score(y_test, y_pred, average='weighted'), 2)
      precision = np.round(precision_score(y_test, y_pred, average='weighted'), 2)
      end_time = time.time()
      time_taken = np.round((end_time - start_time), 2)
      temp_df.loc[len(temp_df)] = [dataset, dataform, X_train.shape[1], str(i).split('.')[-1][:-2], accuracy, f1, recall, precision, time_taken]
  return temp_df

開始訓(xùn)練

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis()
X_train_lda = lda.fit_transform(X_train, y_train)
X_test_lda = lda.transform(X_test)

預(yù)處理、分割和數(shù)據(jù)集的縮放，都與回歸部分相同。在對(duì)8個(gè)不同的數(shù)據(jù)集進(jìn)行新聯(lián)后我們得到了下面結(jié)果:

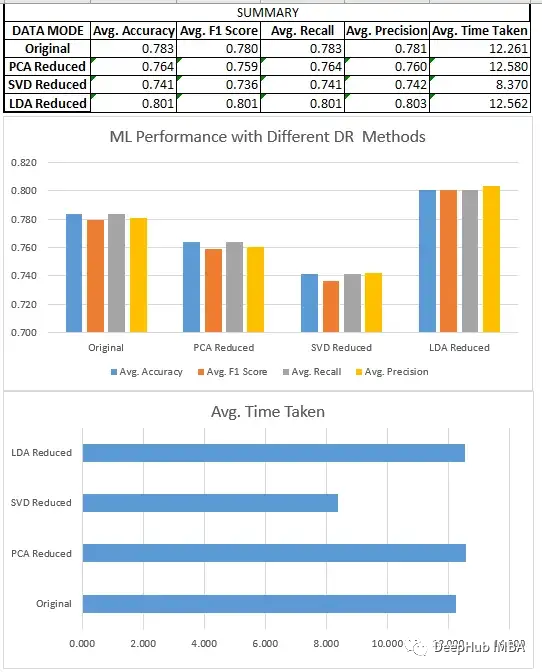
分類模型分析

我們比較了上面所有的三種方法SVD、LDA和PCA。

• LDA數(shù)據(jù)集通常優(yōu)于原始形式的數(shù)據(jù)和由其他降維方法創(chuàng)建的低維數(shù)據(jù)，因?yàn)樗荚谧R(shí)別最有效區(qū)分類的特征的線性組合，而原始數(shù)據(jù)和其他無監(jiān)督降維技術(shù)不關(guān)心數(shù)據(jù)集的標(biāo)簽。
• 降維技術(shù)在應(yīng)用于更大的數(shù)據(jù)集時(shí)，可以極大地減少了數(shù)據(jù)集中的特征數(shù)量，這提高了機(jī)器學(xué)習(xí)模型的效率。在較小的數(shù)據(jù)集上，影響不是特別明顯。除了LDA（它在這些情況下也很有效），因?yàn)樗鼈冊(cè)谝恍┣闆r下，如二元分類，可以將數(shù)據(jù)集的維度減少到只有一個(gè)。
• 當(dāng)我們?cè)趯ふ乙欢ǖ男阅軙r(shí)，LDA可以是分類問題的一個(gè)非常好的起點(diǎn)。
• SVD與回歸一樣，模型的性能下降很明顯。需要調(diào)整n_components的選擇。

總結(jié)

我們比較了一些降維技術(shù)的性能，如奇異值分解(SVD)、主成分分析(PCA)和線性判別分析(LDA)。我們的研究結(jié)果表明，方法的選擇取決于特定的數(shù)據(jù)集和手頭的任務(wù)。

對(duì)于回歸任務(wù)，我們發(fā)現(xiàn)PCA通常比SVD表現(xiàn)得更好。在分類的情況下，LDA優(yōu)于SVD和PCA，以及原始數(shù)據(jù)集。線性判別分析(LDA)在分類任務(wù)中始終擊敗主成分分析(PCA)的這個(gè)是很重要的，但這并不意味著LDA在一般情況下是一種更好的技術(shù)。這是因?yàn)長(zhǎng)DA是一種監(jiān)督學(xué)習(xí)算法，它依賴于有標(biāo)簽的數(shù)據(jù)來定位數(shù)據(jù)中最具鑒別性的特征，而PCA是一種無監(jiān)督技術(shù)，它不需要有標(biāo)簽的數(shù)據(jù)，并尋求在數(shù)據(jù)中保持盡可能多的方差。因此，PCA可能更適合于無監(jiān)督的任務(wù)或可解釋性至關(guān)重要的情況，而LDA可能更適合涉及標(biāo)記數(shù)據(jù)的任務(wù)。

雖然降維技術(shù)可以幫助減少數(shù)據(jù)集中的特征數(shù)量，并提高機(jī)器學(xué)習(xí)模型的效率，但重要的是要考慮對(duì)模型性能和結(jié)果可解釋性的潛在影響。

本文完整代碼：

https://github.com/salmankhi/DimensionalityReduction/blob/main/Notebook_25373.ipynb