POCS：Projections  onto Convex Sets。在數學中，凸集是指其中任意兩點間的線段均在該集合內的集合。而投影則是將某個點映射到另一個空間中的某個子空間上的操作。給定一個凸集合和一個點，可以通過找到該點在該凸集合上的投影來進行操作。該投影是離該點最近的凸集內的點，可以通過最小化該點和凸集內任何其他點之間的距離來計算。既然是投影，那么我們就可以將特征映射到另一個空間中的凸集合上，這樣就可以進行聚類或降維等操作。

本文綜述了一種基于凸集投影法的聚類算法，即基于POCS的聚類算法。原始論文發布在IWIS2022上。

凸集

凸集定義為一個數據點集合，其中連接集合中任意兩點x1和x2的線段完全包含在這個集合中。根據凸集的定義，認為空集?、單集、線段、超平面、歐氏球都被認為是凸集。數據點也被認為是凸集，因為它是單例集（只有一個元素的集合）。這為 POCS 的概念應用于聚類數據點開辟了一條新路徑。

凸集投影(POCS)

POCS方法大致可分為交替式和并行式兩種。

1、交替式poc

從數據空間中的任意一點開始，從該點到兩個(或多個)相交凸集的交替投影將收斂到集合交點內的一點，例如下圖：

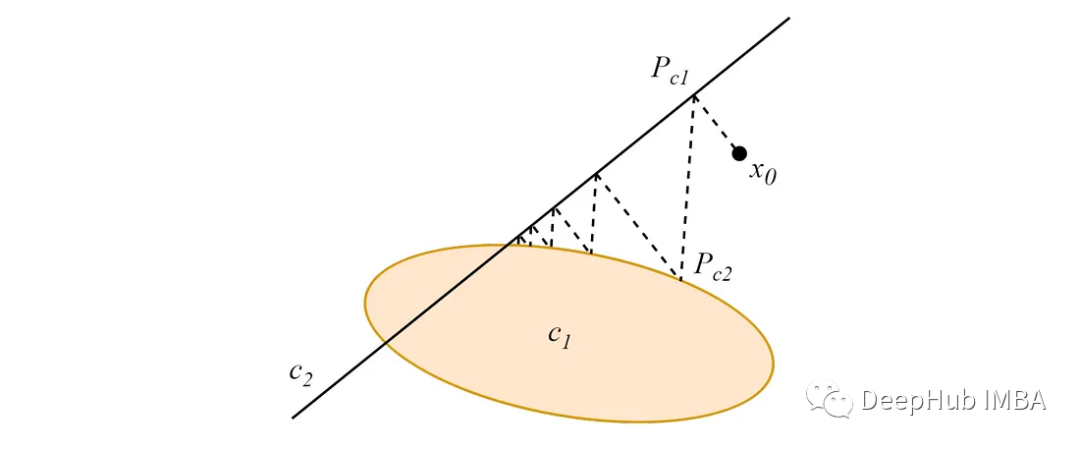
當凸集不相交時，交替投影將收斂到依賴于投影階數的greedy limit cycles。

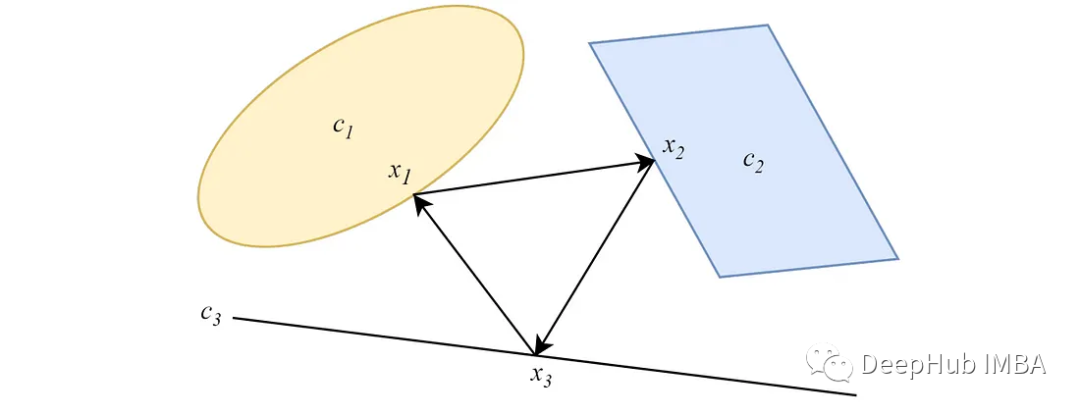
2、并行式 POCS

與交替形式不同，并行的POCS 是從數據點到所有凸集同時進行投影，并且每個投影都有一個重要性權重。對于兩個非空相交凸集，類似于交替式版本，平行投影會收斂到集相交處的一個點。

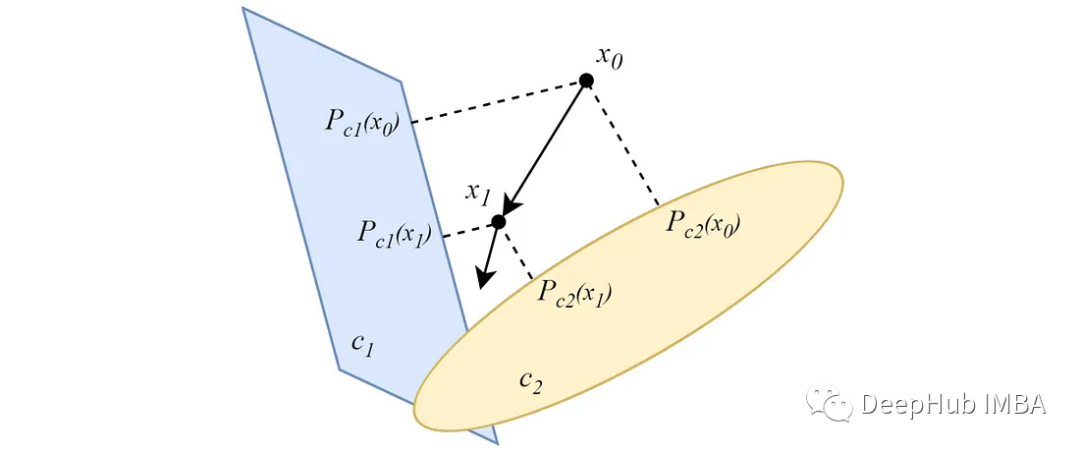
在凸集不相交的情況下，投影將收斂到一個最小解。基于pocs的聚類算法的主要思想來源于這一特性。

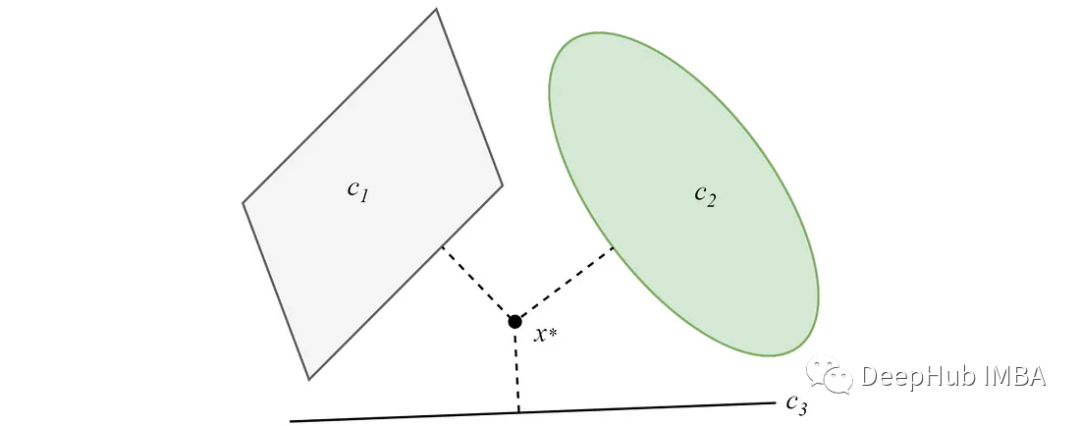
有關POCS的更多細節，可以查看原論文

基于pocs的聚類算法

利用并行POCS方法的收斂性，論文作者提出了一種非常簡單但在一定程度上有效的聚類算法。該算法的工作原理與經典的K-Means算法類似，但在處理每個數據點的方式上存在差異：K-Means算法對每個數據點的重要性加權相同，但是基于pocs的聚類算法對每個數據點的重要性加權不同，這與數據點到聚類原型的距離成正比。

算法的偽代碼如下所示:

實驗結果

作者在一些公共基準數據集上測試了基于pocs的聚類算法的性能。下表總結了這些數據集的描述。

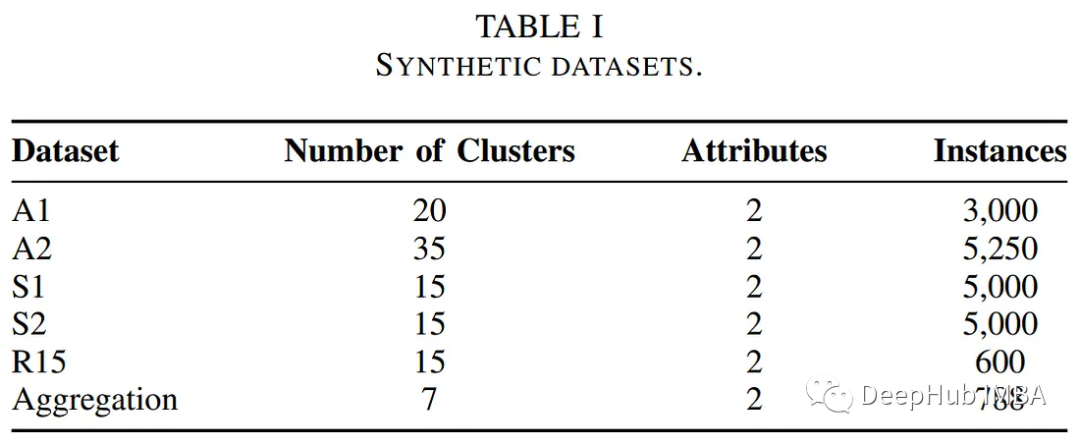
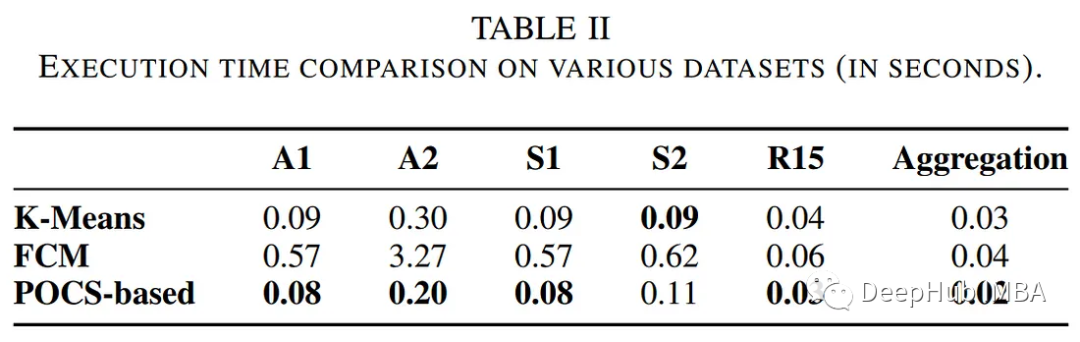
作者比較了基于pocs的聚類算法與其他傳統聚類方法的性能，包括k均值和模糊c均值算法。下表總結了執行時間和聚類錯誤方面的評估。

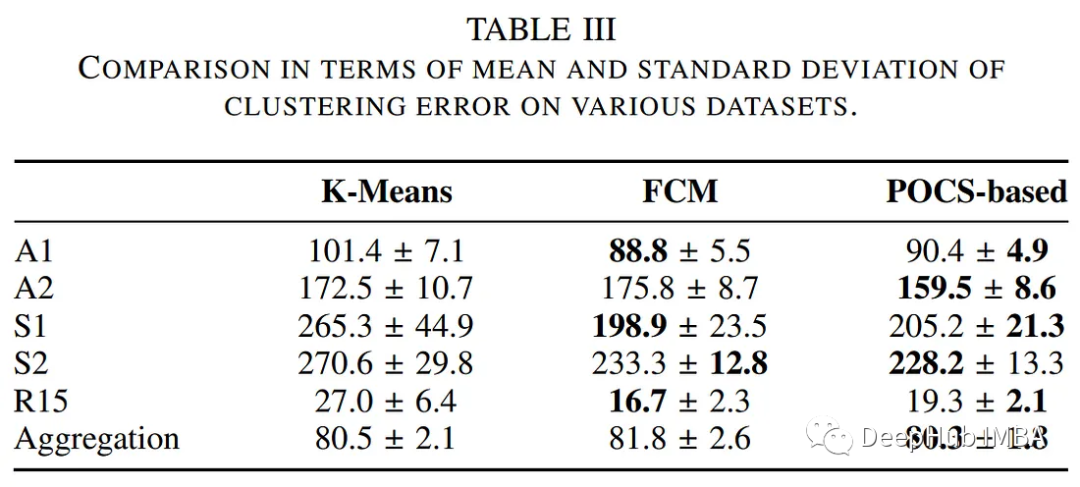
聚類結果如下圖所示：

示例代碼

我們在一個非常簡單的數據集上使用這個算法。作者已經發布了直接使用的包，對于應用我們可以直接使用：

pip install pocs-based-clustering

創建一個以10個簇為中心的5000個數據點的簡單數據集:

# Import packages
 import time
 import matplotlib.pyplot as plt
 
 from sklearn.datasets import make_blobs
 from pocs_based_clustering.tools import clustering
 
 
 # Generate a simple dataset
 num_clusters = 10
 X, y = make_blobs(n_samples=5000, centers=num_clusters, \
                   cluster_std=0.5, random_state=0)
 
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], s=50)
 plt.show()

執行聚類并顯示結果:

# POSC-based Clustering Algorithm
 centroids, labels = clustering(X, num_clusters, 100)
 
 # Display results
 plt.figure(figsize=(8,8))
 plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
 plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red')
 plt.show()

總結

我們簡要回顧了一種簡單而有效的基于投影到凸集(POCS)方法的聚類技術，稱為基于POCS的聚類算法。該算法利用POCS的收斂特性應用于聚類任務，并在一定程度上實現了可行的改進。在一些基準數據集上驗證了該算法的有效性。

論文的地址如下：https://arxiv.org/abs/2208.08888

作者發布的源代碼在這里：https://github.com/tranleanh/pocs-based-clustering