迄今，人們對神經(jīng)網(wǎng)絡(luò)的一大疑慮是，它是難以解釋的黑盒。本文則主要從理論上理解為什么神經(jīng)網(wǎng)絡(luò)對模式識別、分類效果這么好，其本質(zhì)是通過一層層仿射變換和非線性變換把原始輸入做扭曲和變形，直至可以非常容易被區(qū)分不同的類別。 實際上，反向傳播算法（BP) 其實就是根據(jù)訓(xùn)練數(shù)據(jù)不斷地微調(diào)這個扭曲的效果。

大約十年前開 始， 深 度 神經(jīng) 網(wǎng)絡(luò) 在計算 機(jī)視覺等領(lǐng)域取得了突破性成果，引起了極大的興趣和關(guān)注。

然而，仍有一些人對此表示憂慮。原因之一是，神經(jīng)網(wǎng)絡(luò)是一個黑匣子：如果神經(jīng)網(wǎng)絡(luò)訓(xùn)練得很好，可以獲得高質(zhì)量的結(jié)果，但很難理解它的工作原理。如果神經(jīng)網(wǎng)絡(luò)出現(xiàn)故障，也很難找出問題所在。

雖然要整體理解深層神經(jīng)網(wǎng)絡(luò)很難，但可以從低維深層神經(jīng)網(wǎng)絡(luò)入手，也就是每層只有幾個神經(jīng)元的網(wǎng)絡(luò)，它們理解起來要容易得多。我們可以通過可視化方法來理解低維深層神經(jīng)網(wǎng)絡(luò)的行為和訓(xùn)練。可視化方法能讓我們更直觀地了解神經(jīng)網(wǎng)絡(luò)的行為，并觀察到神經(jīng)網(wǎng)絡(luò)和 拓?fù)?nbsp;學(xué)之間的聯(lián)系。

接下來我會談及許多有趣的事情，包括能夠?qū)μ囟〝?shù)據(jù)集進(jìn)行分類的神經(jīng)網(wǎng)絡(luò)的復(fù)雜性下限。

1、一個簡單的例子

讓我們從一個非常簡單的數(shù)據(jù)集開始。下圖中，平面上的兩條曲線由無數(shù)的點組成。神經(jīng)網(wǎng)絡(luò)將試著區(qū)分這些點分別屬于哪一條線。

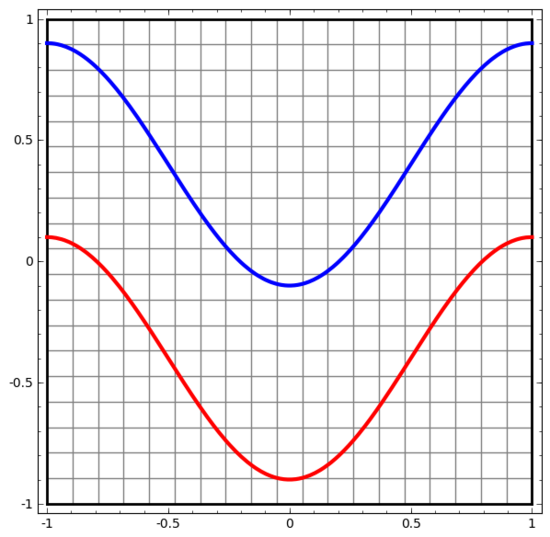
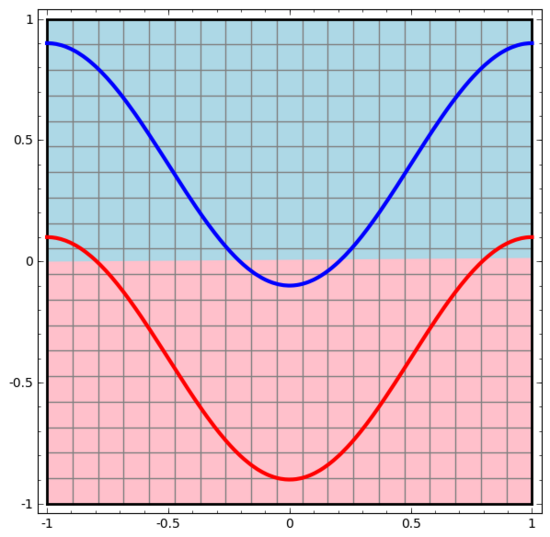
要觀察神經(jīng)網(wǎng)絡(luò)（或任何分類算法）的行為，最直接的方法就是看看它是如何對每個數(shù)據(jù)點進(jìn)行分類的。

我們從最簡單的神經(jīng)網(wǎng)絡(luò)開始觀察，它只有一個輸入層和一個輸出層。這樣的神經(jīng)網(wǎng)絡(luò)只是用一條直線將兩類數(shù)據(jù)點分開。

這樣的神經(jīng)網(wǎng)絡(luò)太簡單粗暴了。現(xiàn)代神經(jīng)網(wǎng)絡(luò)通常在輸入層和輸出層之間有多個層，稱為隱藏層。再簡單的現(xiàn)代神經(jīng)網(wǎng)絡(luò)起碼有一個隱藏層。

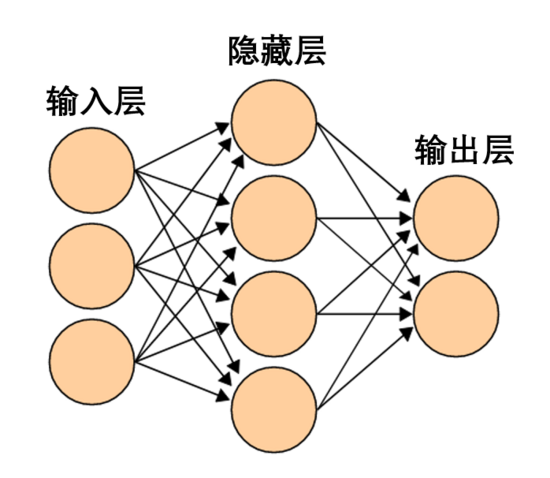
一個簡單的神經(jīng)網(wǎng)絡(luò)，圖源維基百科

同樣地，我們觀察神經(jīng)網(wǎng)絡(luò)對每個數(shù)據(jù)點所做的操作。可見，這個神經(jīng)網(wǎng)絡(luò)用一條曲線而不是直線來分離數(shù)據(jù)點。顯然，曲線比直線更復(fù)雜。

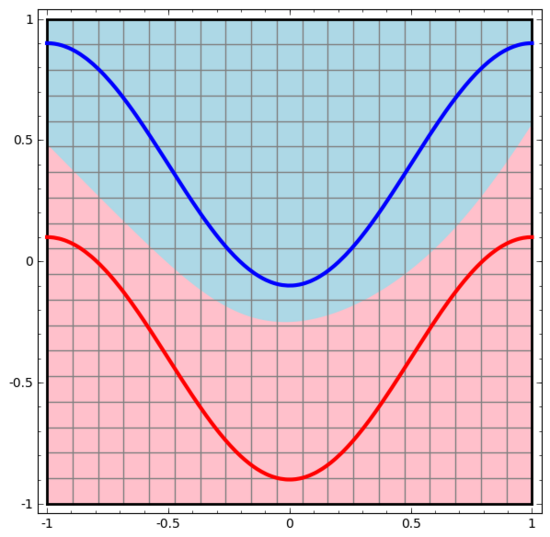
神經(jīng)網(wǎng)絡(luò)的每一層都會用一個新的表示形式來表示數(shù)據(jù)。我們可以觀察數(shù)據(jù)如何轉(zhuǎn)化成新的表示形式以及神經(jīng)網(wǎng)絡(luò)如何對它們進(jìn)行分類。在最后一層的表示形式中，神經(jīng)網(wǎng)絡(luò)會在兩類數(shù)據(jù)之間畫一條線來區(qū)分（如果在更高的維度中，就會畫一個超平面）。

在前面的可視化圖形中，我們看到了數(shù)據(jù)的原始表示形式。你可以把它視為數(shù)據(jù)在「輸入層」的樣子。現(xiàn)在我們看看數(shù)據(jù)被轉(zhuǎn)化之后的樣子，你可以把它視為數(shù)據(jù)在「隱藏層」中的樣子。

數(shù)據(jù)的每一個維度都對應(yīng)神經(jīng)網(wǎng)絡(luò)層中一個神經(jīng)元的激活。

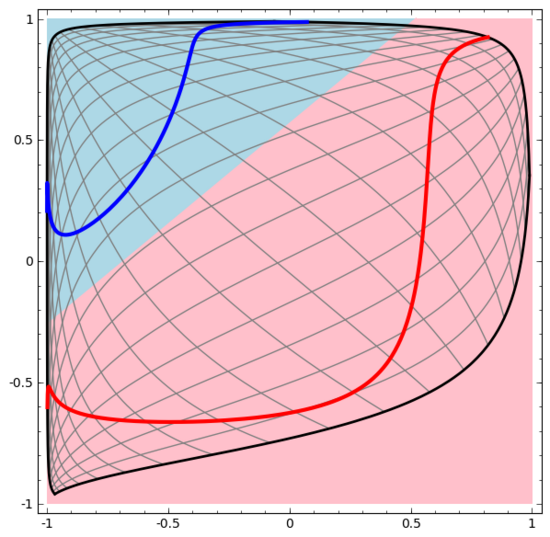
隱藏層用如上方法表示數(shù)據(jù)，使數(shù)據(jù)可以被一條直線分離 （即線性可分）

2、層的連續(xù)可視化

在上一節(jié)的方法中，神經(jīng)網(wǎng)絡(luò)的每一層用不同表示形式來表示數(shù)據(jù)。這樣一來，每層的表示形式之間是離散的，并不連續(xù)。

這就給我們的理解造成困難，從一種表示形式到另一種表示形式，中間是如何轉(zhuǎn)換的呢？好在，神經(jīng)網(wǎng)絡(luò)層的特性讓這方面的理解變得非常容易。

神經(jīng)網(wǎng)絡(luò)中有各種不同的層。下面我們將以tanh層作為具體例子討論。一個tanh層 ，包括：

• 用“權(quán)重”矩陣 W 作線性變換
• 用向量 b 作平移
• 用 tanh 逐點表示

我們可以將其視為一個連續(xù)的轉(zhuǎn)換，如下所示：

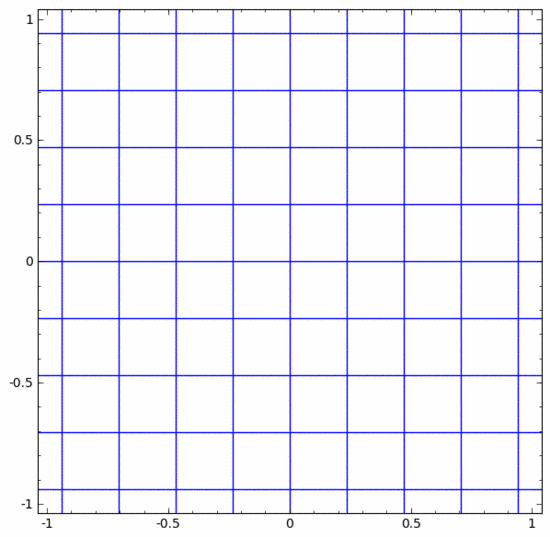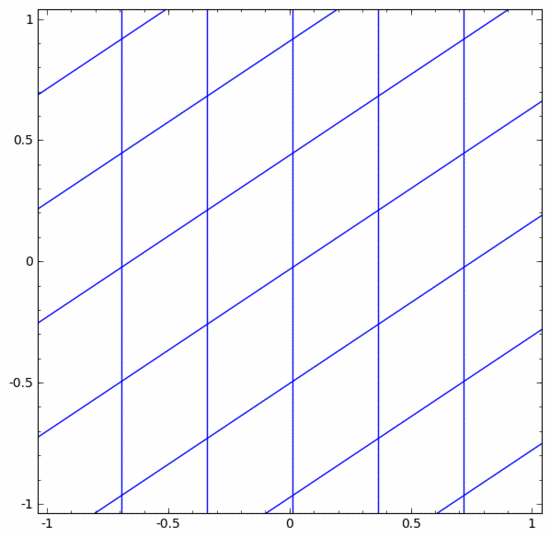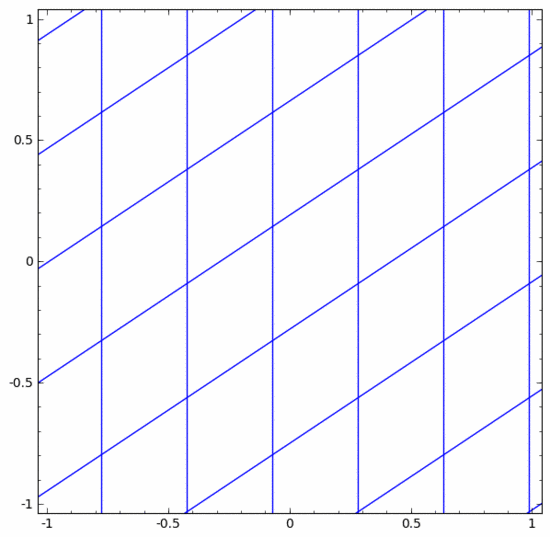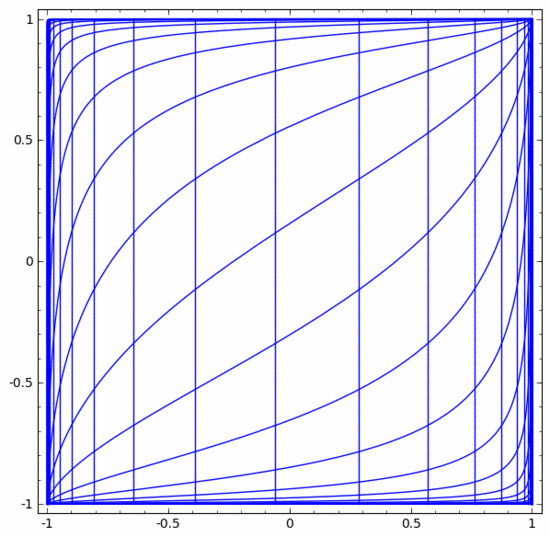
其他標(biāo)準(zhǔn)層的情況大致相同，由仿射變換和單調(diào)激活函數(shù)的逐點應(yīng)用組成。

我們可以用這種方法來理解更復(fù)雜的神經(jīng)網(wǎng)絡(luò)。例如，下面的神經(jīng)網(wǎng)絡(luò)使用四個隱藏層對兩條略有互纏的螺旋線進(jìn)行分類。可以看到，為了對數(shù)據(jù)進(jìn)行分類，數(shù)據(jù)的表示方式被不斷轉(zhuǎn)換。兩條螺旋線最初是糾纏在一起的，但到最后它們可以被一條直線分離（線性可分）。

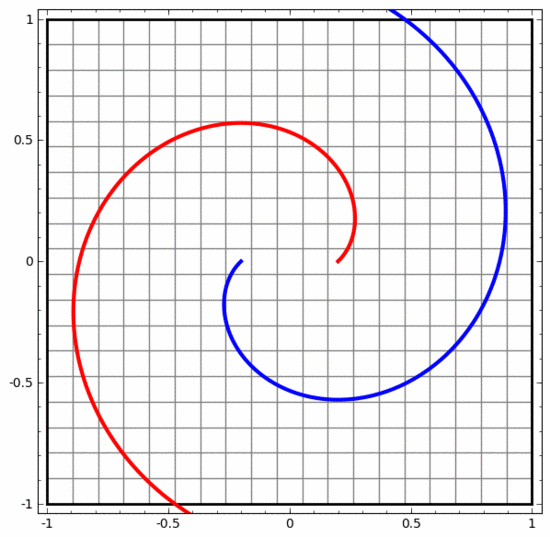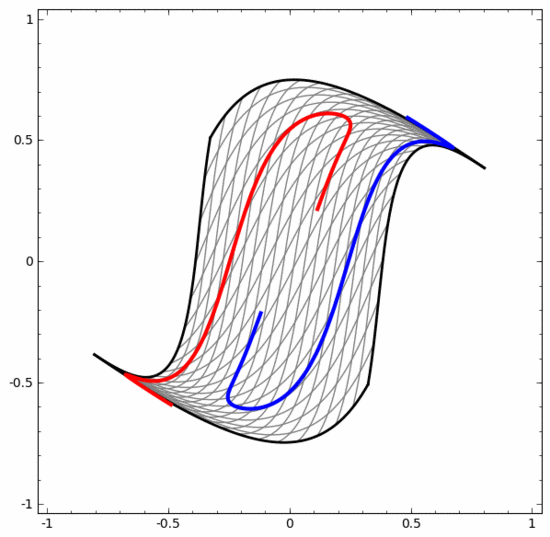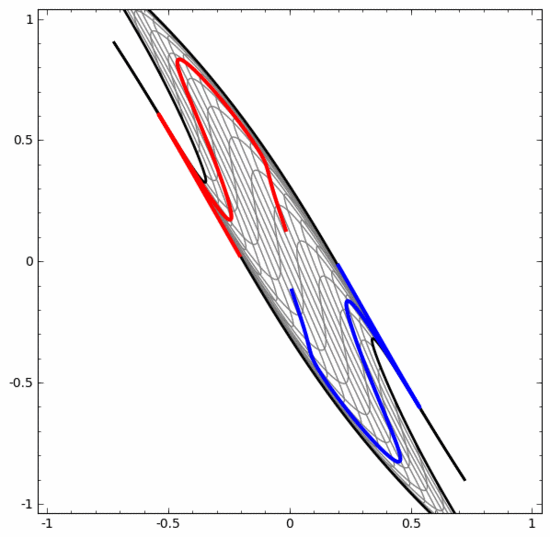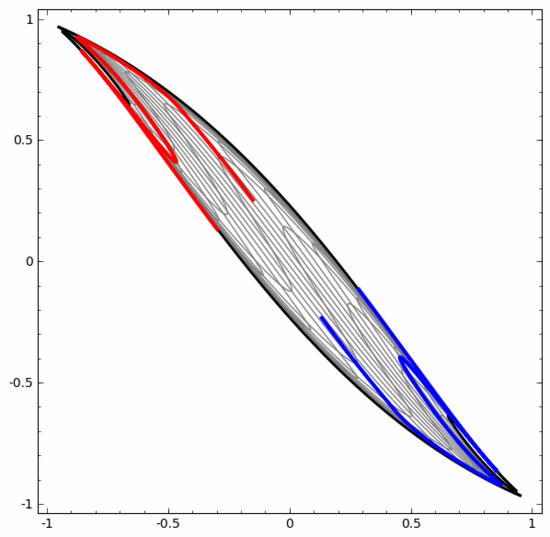
另一方面，下面的神經(jīng)網(wǎng)絡(luò)，雖然也使用多個隱藏層，卻無法劃分兩條互纏程度更深的螺旋線。

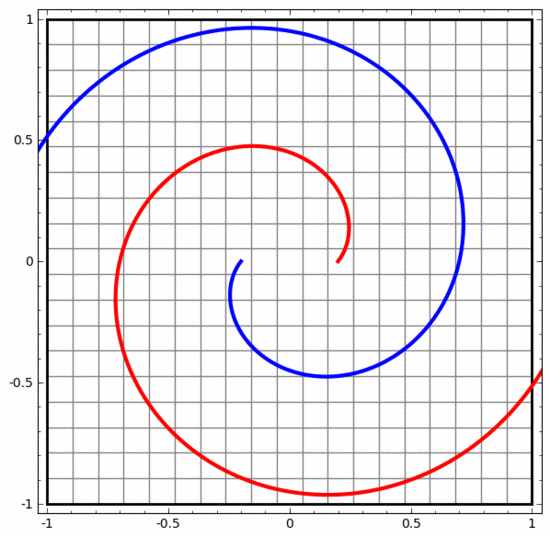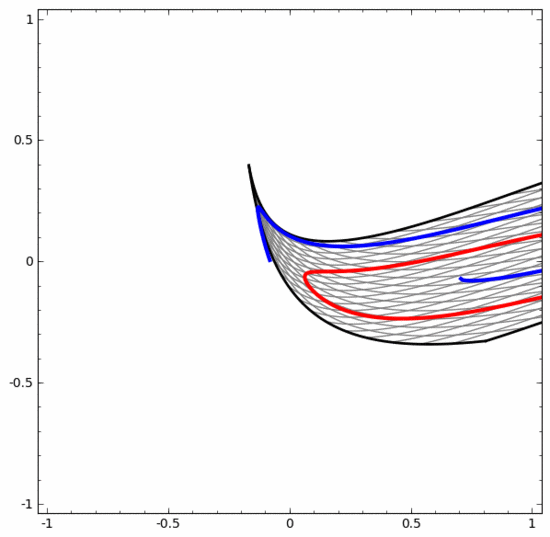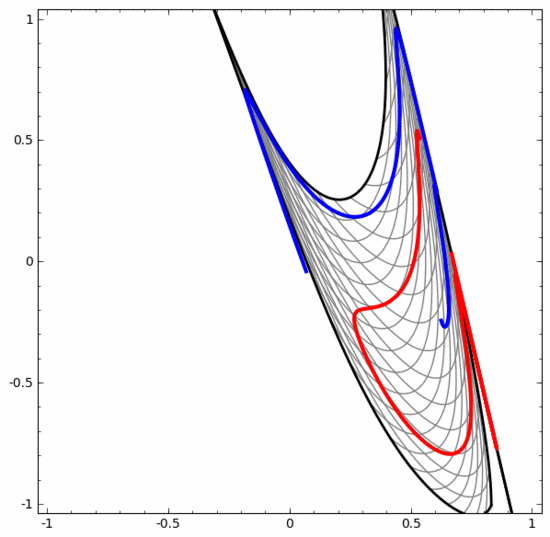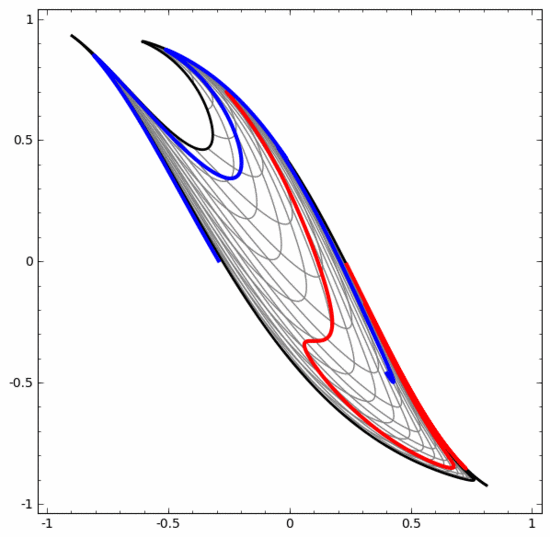
需要明確指出的是，以上兩個螺旋線分類任務(wù)有一些挑戰(zhàn)，因為我們現(xiàn)在使用的只是低維神經(jīng)網(wǎng)絡(luò)。如果我們使用寬度更大的神經(jīng)網(wǎng)絡(luò)，一切都會很容易很多。

（Andrej Karpathy基于ConvnetJS制作了一個很好的demo，讓人可以通過這種可視化的訓(xùn)練交互式地探索神經(jīng)網(wǎng)絡(luò)。）

3、tanh層的拓?fù)?/h4>

神經(jīng)網(wǎng)絡(luò)的每一層都會拉伸和擠壓空間，但它不會剪切、割裂或折疊空間。直觀上看，神經(jīng)網(wǎng)絡(luò)不會破壞數(shù)據(jù)的拓?fù)湫再|(zhì)。例如，如果一組數(shù)據(jù)是連續(xù)的，那么它被轉(zhuǎn)換表示形式之后也是連續(xù)的（反之亦然）。

像這樣不影響拓?fù)湫再|(zhì)的變換稱為同胚（homeomorphisms）。形式上，它們是雙向連續(xù)函數(shù)的雙射。

定理 ：如果權(quán)重矩陣 W 是非奇異的（non-singular），而神經(jīng)網(wǎng)絡(luò)的一層有N個輸入和N個輸出，那么這層的映射是同胚（對于特定的定義域和值域而言）。

證明 ：讓我們一步一步來：

1. 假設(shè) W 存在非零行列式。那么它是一個具有線性逆的雙射線性函數(shù)。線性函數(shù)是連續(xù)的。那么“乘以 W ”這樣的變換就是同胚；

2. “平移”變換是同胚；

3. tanh（還有s igmoid和softplus，但不包括ReLU）是具有連續(xù)逆（continuous inverses）的 連續(xù)函數(shù)。（對于特定的定義域和值域而言），它們就是雙射，對它們的逐點應(yīng)用就是同胚。

因此，如果 W 存在一個非零行列式，這一個神經(jīng)網(wǎng)絡(luò)層就是同胚。

如果我們將這樣的層隨意組合在一起，這個結(jié)果仍然成立。

4、拓?fù)渑c分類

我們來看一個二維數(shù)據(jù)集，它包含兩類數(shù)據(jù)A和B：

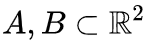
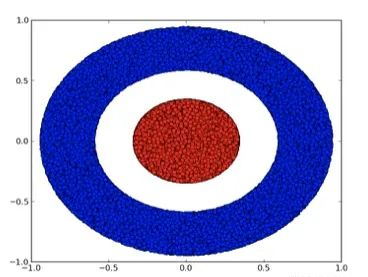
A是紅色，B是藍(lán)色

說明 ：要對這個數(shù)據(jù)集進(jìn)行分類，神經(jīng)網(wǎng)絡(luò)（不管深度如何）必須有一個包含3個或以上隱藏單元的層。

如前所述，使用sigmoid單元或softmax層進(jìn)行分類，相當(dāng)于在最后一層的表示形式中找到一個超平面（在本例中則是直線）來分隔 A 和 B。如果只有兩個隱藏單元，神經(jīng)網(wǎng)絡(luò)在拓?fù)渖暇蜔o法以這種方式分離數(shù)據(jù)，也就無法對上述數(shù)據(jù)集進(jìn)行分類。

在下面的可視化中，隱藏層轉(zhuǎn)換對數(shù)據(jù)的表示形式，直線為分割線。可見，分割線不斷旋轉(zhuǎn)、移動，卻始終無法很好地分隔A和B兩類數(shù)據(jù)。

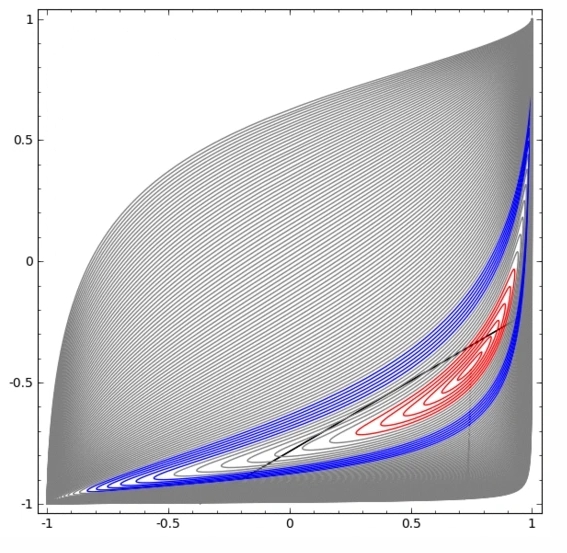
這樣的神經(jīng)網(wǎng)絡(luò)再怎么訓(xùn)練也無法很好地完成分類任務(wù)

最后它只能勉強(qiáng)實現(xiàn)一個局部最小值，達(dá)到80%的分類精度。

上述例子只有一個隱藏層，由于只有兩個隱藏單元，所以無論如何它都會分類失敗。

證明 ：如果只有兩個隱藏單元，要么這層的轉(zhuǎn)換是同胚，要么層的權(quán)重矩陣有行列式0。如果是同胚的話，A仍然被B包圍，不能用一條直線把A和B分開。如果有行列式0，那么數(shù)據(jù)集將在某個軸上發(fā)生折疊。因為A被B包圍，所以A在任何軸上折疊都會導(dǎo)致部分A數(shù)據(jù)點與B混合，致使無法區(qū)分A和B。

但如果我們添加第三個隱藏單元，問題就迎刃而解了。此時，神經(jīng)網(wǎng)絡(luò)可以將數(shù)據(jù)轉(zhuǎn)換成如下表示形式：

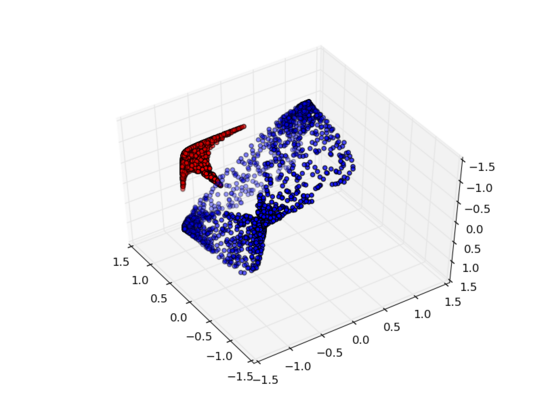
這時就可以用一個超平面來分隔A和B了。

為了更好地解釋其原理，此處用一個更簡單的一維數(shù)據(jù)集舉例：

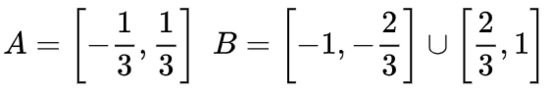
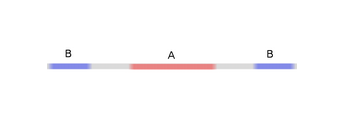
要對這個數(shù)據(jù)集進(jìn)行分類，必須使用由兩個或以上隱藏單元組成的層。如果使用兩個隱藏單元，就可以用一條漂亮的曲線來表示數(shù)據(jù)，這樣就可以用一條直線來分隔A和B：

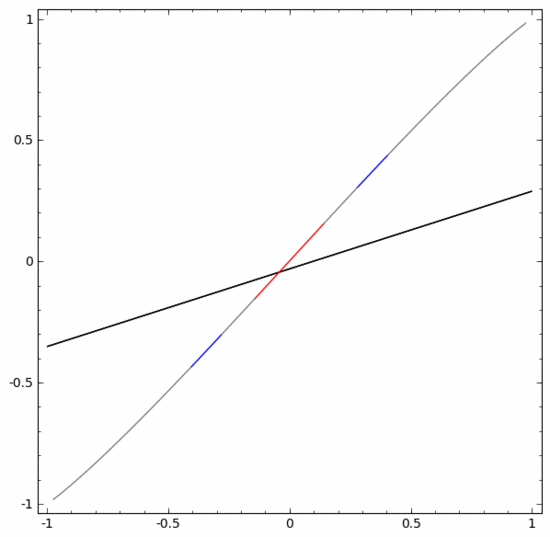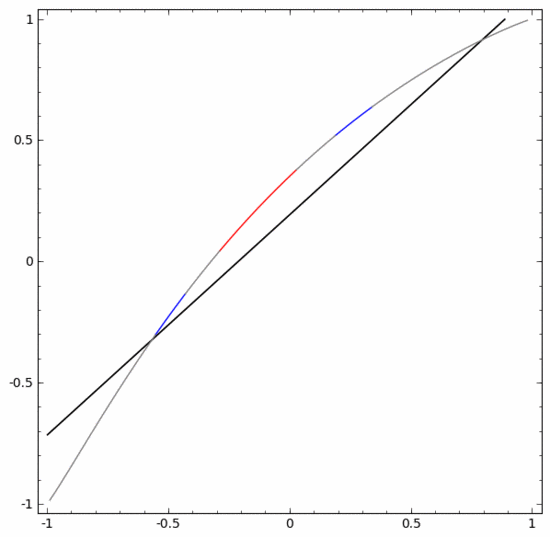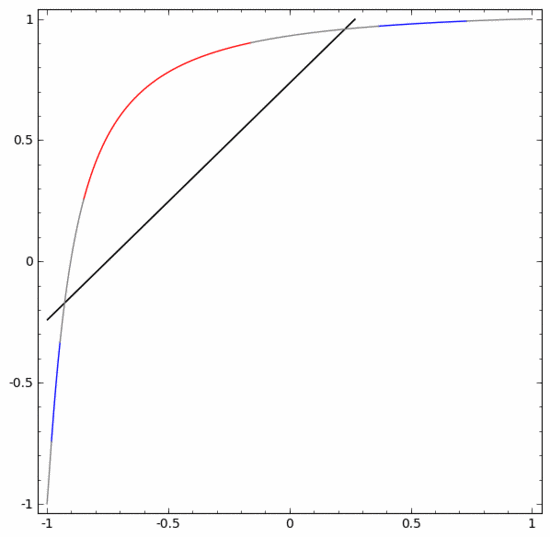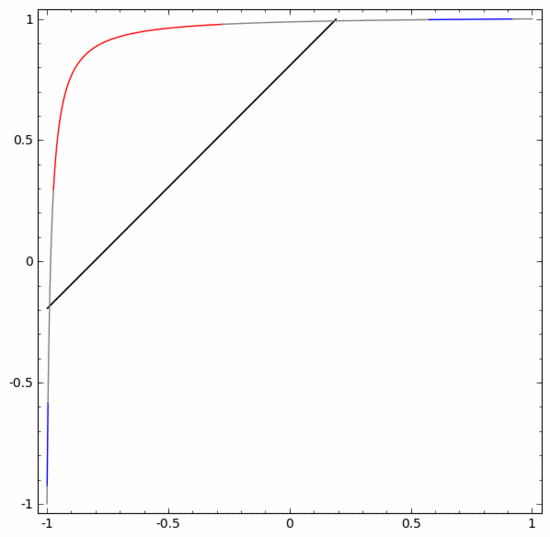
這是怎么做到的呢？當(dāng) 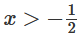時，其中一個隱藏單元被激活；當(dāng)  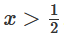時，另一個隱藏單元被激活。當(dāng)前一個隱藏單元被激活而后一個隱藏單元未被激活時，就可以判斷出這是屬于A的數(shù)據(jù)點。

5、流形假說

流形假說對處理真實世界的數(shù)據(jù)集（比如圖像數(shù)據(jù)）有意義嗎？我認(rèn)為有意義。

流形假設(shè)是指自然數(shù)據(jù)在其嵌入空間中形成低維流形。這一假設(shè)具備理論和實驗支撐。如果你相信流形假設(shè)，那么分類算法的任務(wù)就可以歸結(jié)為分離一組互相糾纏的流形。

在前面的示例中，一個類完全包圍了另一個類。然而，在真實世界的數(shù)據(jù)中，狗的圖像流形不太可能被貓的圖像流形完全包圍。但是，其他更合理的拓?fù)淝闆r依然可能會引發(fā)問題，下一節(jié)將會詳談。

6、鏈接與同倫

下面我將談?wù)劻硪环N有趣的數(shù)據(jù)集：兩個互相鏈接的圓環(huán)面（tori），A 和 B。

與我們之前談到的數(shù)據(jù)集情況類似，如果不使用n+1維度，就不能分離一個n維的數(shù)據(jù)集（n+1維度在本例中即為第4維度）。

鏈接問題屬于拓?fù)鋵W(xué)中的紐結(jié)理論。有時候，我們看到一個鏈接，并不能立馬判斷它是否是一個斷鏈（unlink斷鏈的意思是，雖然它們互相糾纏，但可以通過連續(xù)變形將其分離）。

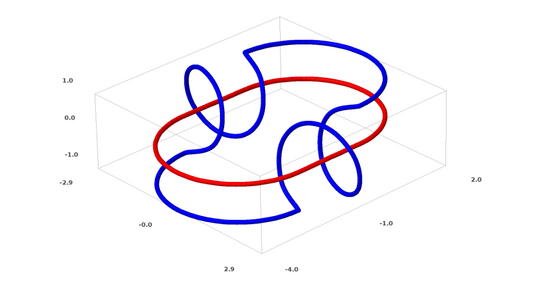
一個較簡單的斷鏈

如果隱藏層只有3個隱藏單元的神經(jīng)網(wǎng)絡(luò)可以對一個數(shù)據(jù)集進(jìn)行分類，那么這個數(shù)據(jù)集就是一個斷鏈（問題來了：從理論上講，所有斷鏈都可以被只有3個隱藏單元的神經(jīng)網(wǎng)絡(luò)分類嗎？）。

從紐結(jié)理論的角度來看，神經(jīng)網(wǎng)絡(luò)產(chǎn)生的數(shù)據(jù)表示形式的連續(xù)可視化不僅僅是一個很好的動畫，也是一個解開鏈接的過程。在拓?fù)鋵W(xué)中，我們稱之為原始鏈接和分離后的鏈接之間的環(huán)繞同痕（ambient isotopy）。

流形A和流形B之間的環(huán)繞同痕是一個連續(xù)函數(shù)：

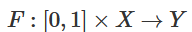
每個 是X的同胚。 是特征函數(shù)， 將A映射到B。也就是說， 不斷從將A映射到自身過渡到將A映射到B。

定理 ：如果同時滿足以下三個條件：(1)W為非奇異；(2)可以手動排列隱藏層中神經(jīng)元的順序；(3)隱藏單元的數(shù)量大于1，那么神經(jīng)網(wǎng)絡(luò)的輸入和神經(jīng)網(wǎng)絡(luò)層產(chǎn)生的表示形式之間有一個環(huán)繞同痕。

證明 ：我們同樣一步一步來：

1. 最難的部分是線性轉(zhuǎn)換。為了實現(xiàn)線性轉(zhuǎn)換，我們需要W有一個正行列式。我們的前提是行列式為非零，如果行列式為負(fù)，我們可以通過調(diào)換兩個隱藏神經(jīng)元將其轉(zhuǎn)化為正。正行列式矩陣的空間是路徑連接的（path-connected），這就有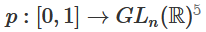， 因此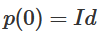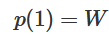，，。通過函數(shù)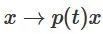，我們可以連續(xù)地將特征函數(shù)過渡到W轉(zhuǎn)換，在時間t在每個點將x與連續(xù)過渡的矩陣 相乘。

2. 可以通過函數(shù)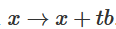從特征函數(shù)過渡到b平移。

3. 可以通過函數(shù)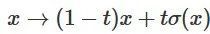從特征函數(shù)過渡到 的逐點應(yīng)用。

我猜可能有人會對下面這個問題感興趣：能不能研發(fā)出可自動發(fā)現(xiàn)這種環(huán)繞同痕 （ambient isotopy）的 程序，還能自動證明某些不同鏈接的等效性或某些鏈接的可分離性。我也很想知道神經(jīng)網(wǎng)絡(luò)在這方面能不能打敗目前的SOTA技術(shù)。

雖然我們現(xiàn)在所談的鏈接形式很可能不會在現(xiàn)實世界的數(shù)據(jù)中出現(xiàn)，但現(xiàn)實的數(shù)據(jù)可能存在更高維度的泛化。

鏈接和紐結(jié)都是1維的流形，但需要4個維度才能將它們分離。同樣，要分離n維的流形，就需要更高維度的空間。所有的n維流形都可以用2n+2個維度分離。

7、一個簡單的方法

對于神經(jīng)網(wǎng)絡(luò)來說，最簡單的方法就是將互纏的流形直接拉開，而且將那些纏結(jié)在一起的部分拉得越細(xì)越好。雖然這不是我們追求的根本性解決方案，但它可以實現(xiàn)相對較高的分類精度，達(dá)到一個相對理想的局部最小值。

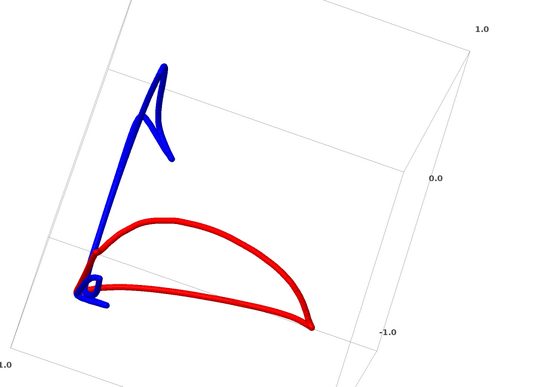
這種方法會導(dǎo)致試圖拉伸的區(qū)域出現(xiàn)非常高的導(dǎo)數(shù)。應(yīng)對這一點需要采用收縮懲罰，也就是懲罰數(shù)據(jù)點的層的導(dǎo)數(shù)。

局部極小值對解決拓?fù)鋯栴}并無用處，不過拓?fù)鋯栴}或許可以為探索解決上述問題提供好的思路。

另一方面，如果我們只關(guān)心取得好的分類結(jié)果，那么假如流形有一小部分與另一個流形互相纏繞，這對我們來說是個問題嗎？如果我們只在乎分類結(jié)果，那么這似乎不成問題。

（我的直覺認(rèn)為，像這樣走捷徑的方法并不好，容易走進(jìn)死胡同。特別是，在優(yōu)化問題中，尋求局部極小值并不能真正解決問題，而如果選擇一個不能真正解決問題的方案，就終將不能取得良好的性能。）

8、選取更適合操縱流形的神經(jīng)網(wǎng)絡(luò)層？

我認(rèn)為標(biāo)準(zhǔn)的神經(jīng)網(wǎng)絡(luò)層并不適合操縱流形，因為它們使用的是仿射變換和逐點激活函數(shù)。

或許我們可以使用一種完全不同的神經(jīng)網(wǎng)絡(luò)層？

我腦海中浮現(xiàn)的一個想法是，首先，讓神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)一個向量場，向量場的方向是我們想要移動流形的方向：

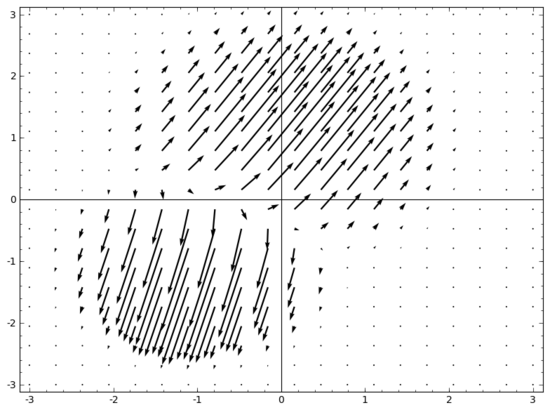
然后在此基礎(chǔ)上變形空間：

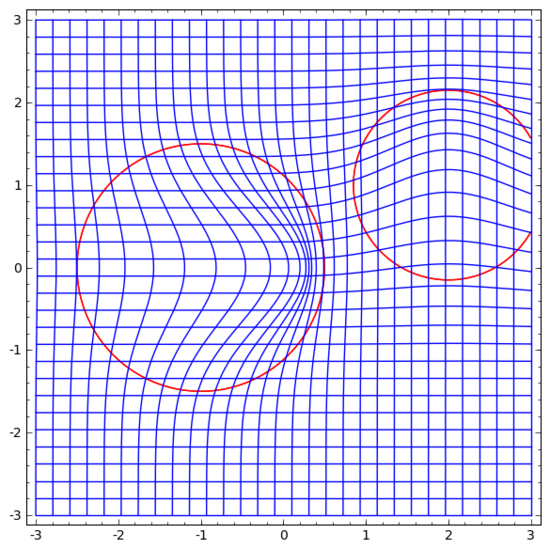
我們可以在固定點學(xué)習(xí)向量場（只需從訓(xùn)練集中選取一些固定點作為錨），并以某種方式進(jìn)行插值。上面的向量場的形式如下：

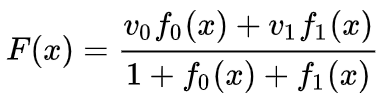
其中 和 是向量， 和 是n維高斯函數(shù)。這一想法受到徑向基函數(shù)的啟發(fā)。

9、K-近鄰層

我的另一觀點是，對神經(jīng)網(wǎng)絡(luò)而言，線性可分性可能是一個過高且不合理的要求，或許使用k近鄰（k-NN）會更好。然而，k-NN算法很大程度上依賴數(shù)據(jù)的表示形式，因此，需要有良好的數(shù)據(jù)表示形式才能讓k-NN算法取得好結(jié)果。

在第一個實驗中，我訓(xùn)練了一些MNIST神經(jīng)網(wǎng)絡(luò)（兩層CNN，無dropout），錯誤率低于1%。然后，我丟棄了最后的softmax層，使用了k-NN算法，多次結(jié)果顯示，錯誤率降低了0.1-0.2%。

不過，我感覺這種做法依然不對。神經(jīng)網(wǎng)絡(luò)仍然在嘗試線性分類，只不過由于使用了k-NN算法，所以能夠略微修正一些它所犯的錯誤，從而降低錯誤率。

由于（1/distance）的加權(quán)，k-NN對于它所作用的數(shù)據(jù)表示形式是可微的。因此，我們可以直接訓(xùn)練神經(jīng)網(wǎng)絡(luò)進(jìn)行k-NN分類。這可以視為一種“最近鄰”層，它的作用與softmax層類似。

我們不想為每個小批量反饋整個訓(xùn)練集，因為這樣計算成本太高。我認(rèn)為一個很好的方法是，根據(jù)小批量中其他元素的類別對小批量中的每個元素進(jìn)行分類，給每個元素賦予（1/(與分類目標(biāo)的距離)）的權(quán)重。

遺憾的是，即使使用復(fù)雜的架構(gòu)，使用k-NN算法也只能把錯誤率降低至4-5%，而使用簡單的架構(gòu)錯誤率則更高。不過，我并未在超參數(shù)方面下太多工夫。

但我還是很喜歡k-NN算法，因為它更適合神經(jīng)網(wǎng)絡(luò)。我們希望同一流形的點彼此更靠近，而不是執(zhí)著于用超平面把流形分開。這相當(dāng)于使單個流形收縮，同時使不同類別的流形之間的空間變大。這樣就把問題簡化了。

10、總結(jié)

數(shù)據(jù)的某些拓?fù)涮匦钥赡軐?dǎo)致這些數(shù)據(jù)不能使用低維神經(jīng)網(wǎng)絡(luò)來進(jìn)行線性分離（無論神經(jīng)網(wǎng)絡(luò)深度如何）。即使在技術(shù)可行的情況下，例如螺旋，用低維神經(jīng)網(wǎng)絡(luò)也非常難以實現(xiàn)分離。

為了對數(shù)據(jù)進(jìn)行精確分類，神經(jīng)網(wǎng)絡(luò)有時需要更寬的層。此外，傳統(tǒng)的神經(jīng)網(wǎng)絡(luò)層不適合操縱流形；即使人工設(shè)置權(quán)重，也很難得到理想的數(shù)據(jù)轉(zhuǎn)換表示形式。新的神經(jīng)網(wǎng)絡(luò)層或許能起到很好的輔助作用，特別是從流形角度理解機(jī)器學(xué)習(xí)啟發(fā)得出的新神經(jīng)網(wǎng)絡(luò)層。