谷歌:大模型不僅有涌現能力,訓練時間長了還有「領悟」能力
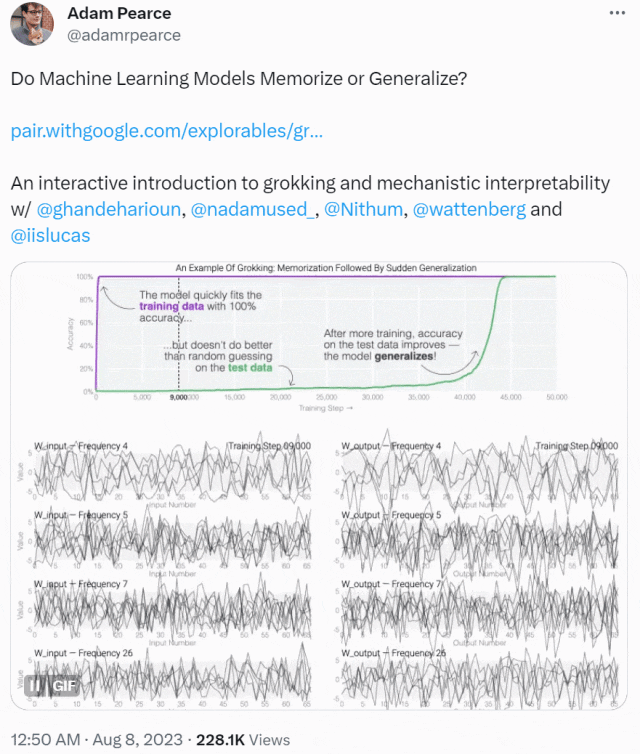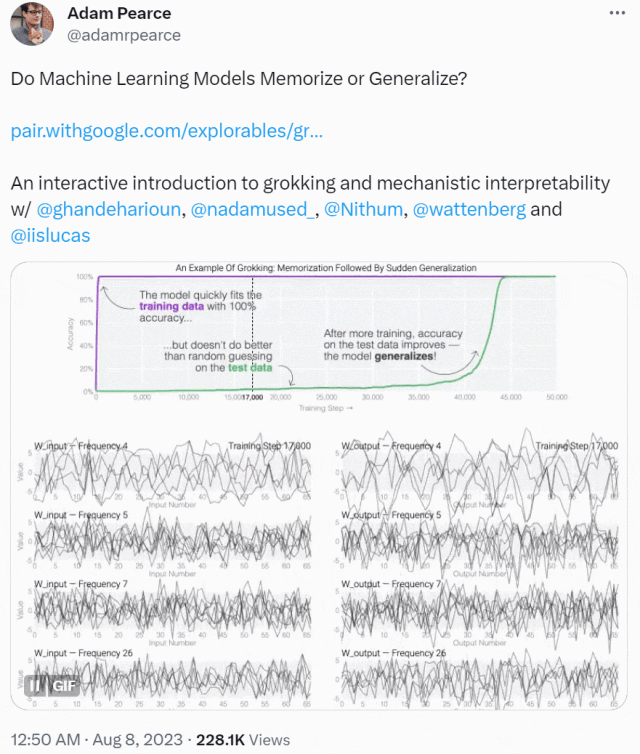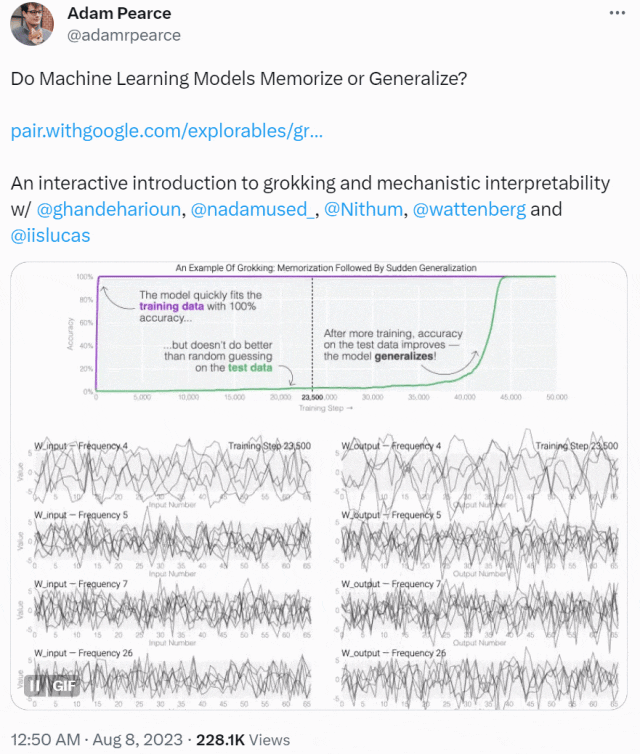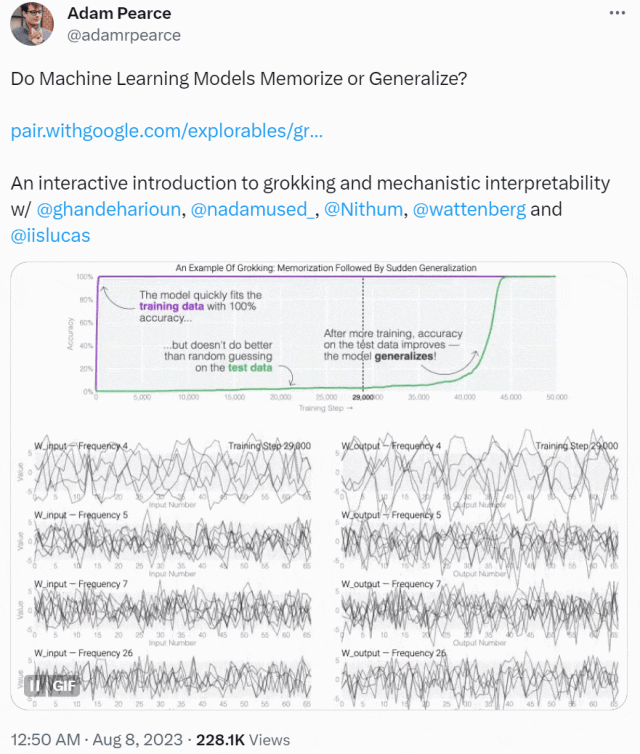
2021 年,研究人員在訓練一系列微型模型時取得了一個驚人的發現,即模型經過長時間的訓練后,會有一個變化,從開始只會「記憶訓練數據」,轉變為對沒見過的數據也表現出很強的泛化能力。
這種現象被稱為「領悟(grokking)」,如下圖所示,模型在長時間擬合訓練數據后,「領悟」現象會突然出現。
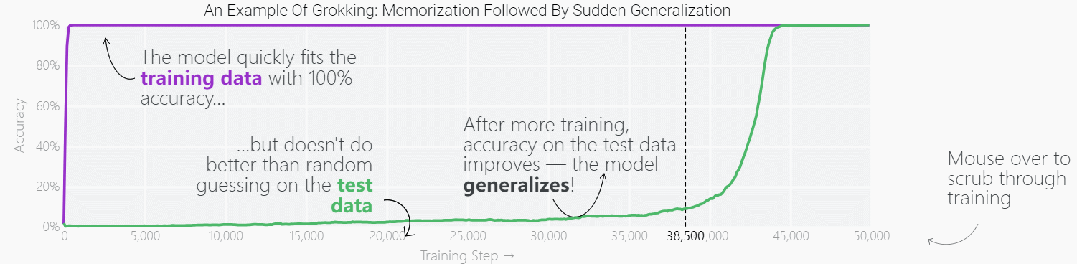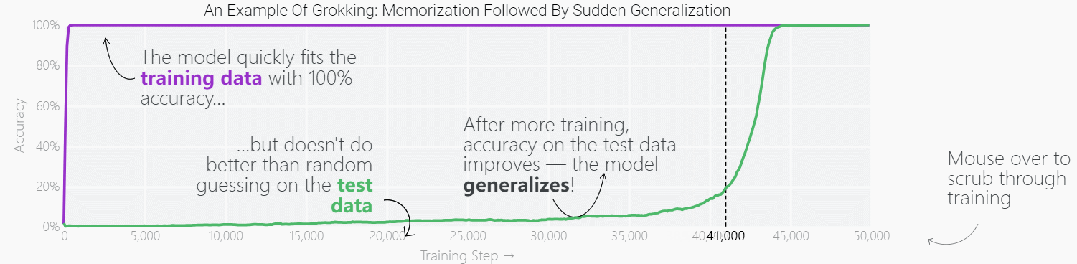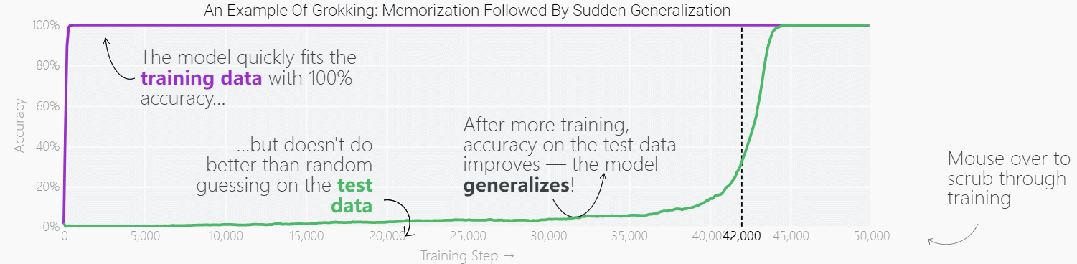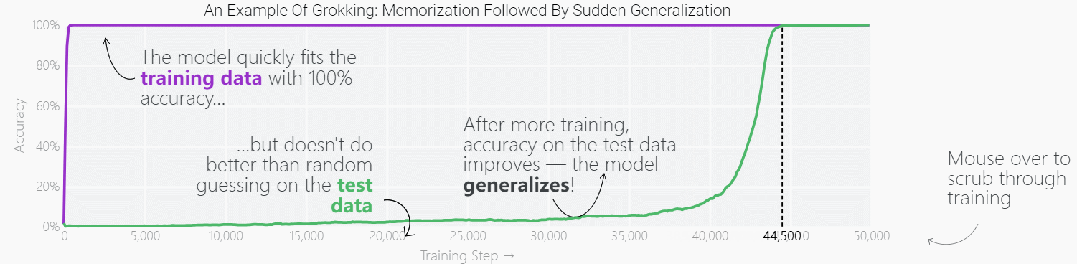 圖片
圖片
既然微型模型有這種特性,那么更復雜一點的模型在經過更長時間的訓練后,是否也會突然出現「領悟」現象?最近大型語言模型(LLM)發展迅猛,它們看起來對世界有著豐富的理解力,很多人認為 LLM 只是在重復所記憶的訓練內容,這一說法正確性如何,我們該如何判斷 LLM 是輸出記憶內容,還是對輸入數據進行了很好的泛化?
為了更好的了解這一問題,本文來自谷歌的研究者撰寫了一篇博客,試圖弄清楚大模型突然出現「領悟」現象的真正原因。
 圖片
圖片
本文先從微型模型的訓練動態開始,他們設計了一個具有 24 個神經元的單層 MLP,訓練它們學會做模加法(modular addition)任務,我們只需知道這個任務的輸出是周期性的,其形式為 (a + b) mod n。
MLP 模型權重如下圖所示,研究發現模型的權重最初非常嘈雜,但隨著時間的增加,開始表現出周期性。
 圖片
圖片
如果將單個神經元的權重可視化,這種周期性變化更加明顯:
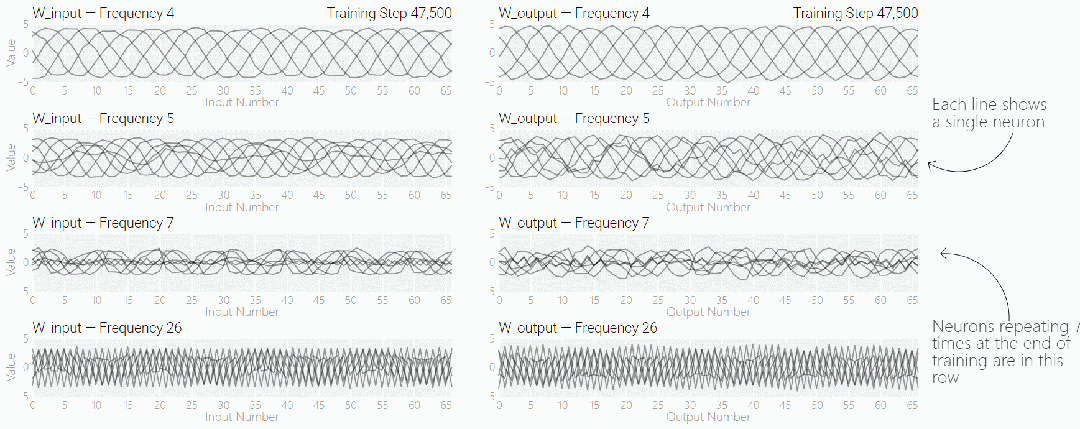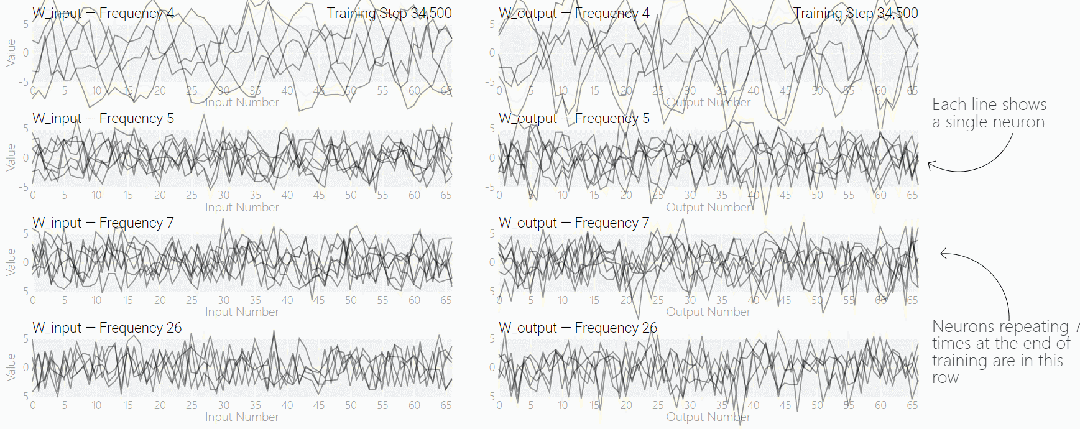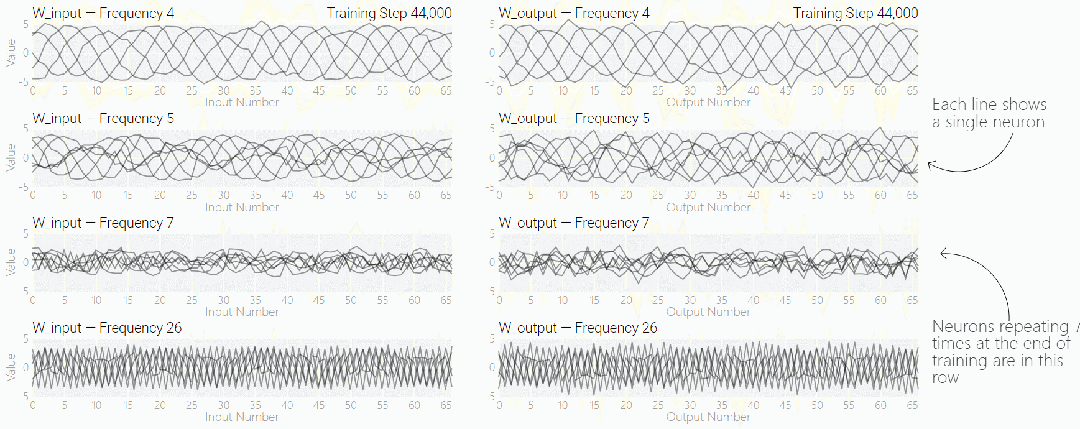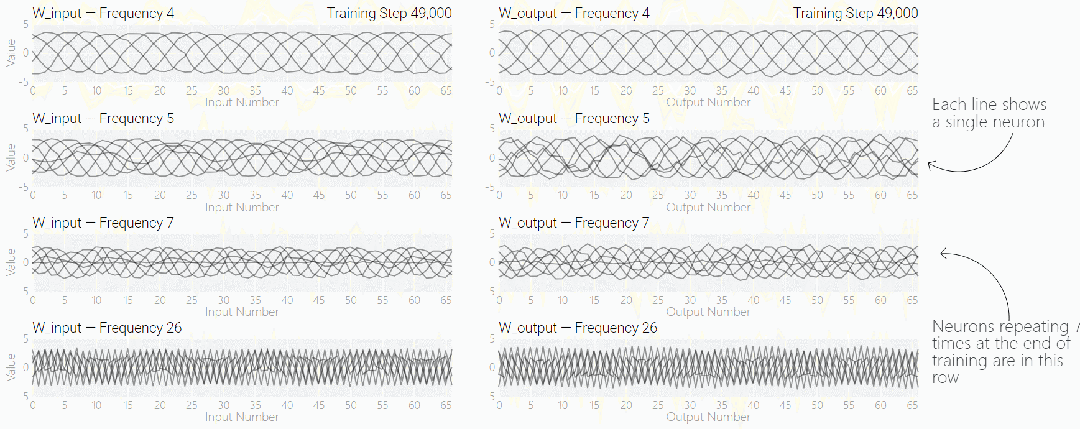 圖片
圖片
別小看周期性,權重的周期性表明該模型正在學習某種數學結構,這也是模型從記憶數據轉變為具有泛化能力的關鍵。很多人對這一轉變感到迷惑,為什么模型會從記憶數據模式轉變為泛化數據模式。
用 01 序列進行實驗
為了判斷模型是在泛化還是記憶,該研究訓練模型預測 30 個 1 和 0 隨機序列的前三位數字中是否有奇數個 1。例如 000110010110001010111001001011 為 0,而 010110010110001010111001001011 為 1。這基本就是一個稍微棘手的 XOR 運算問題,帶有一些干擾噪聲。如果模型在泛化,那么應該只使用序列的前三位數字;而如果模型正在記憶訓練數據,那么它還會使用后續數字。
該研究使用的模型是一個單層 MLP,在 1200 個序列的固定批上進行訓練。起初,只有訓練準確率有所提高,即模型會記住訓練數據。與模運算一樣,測試準確率本質上是隨機的,隨著模型學會通用解決方案而急劇上升。
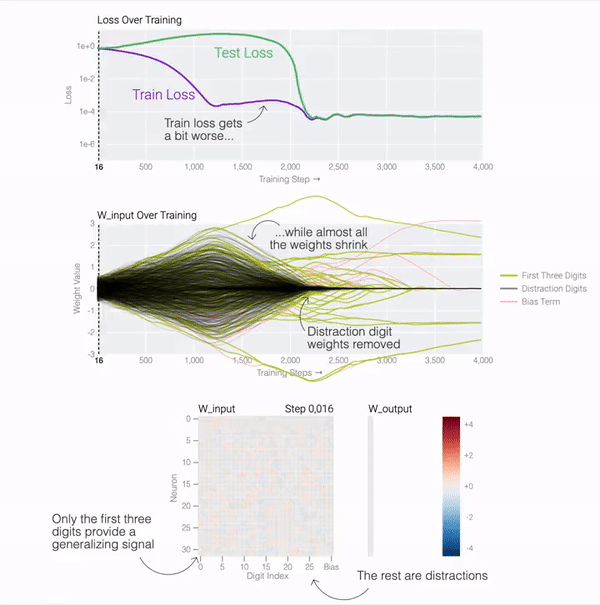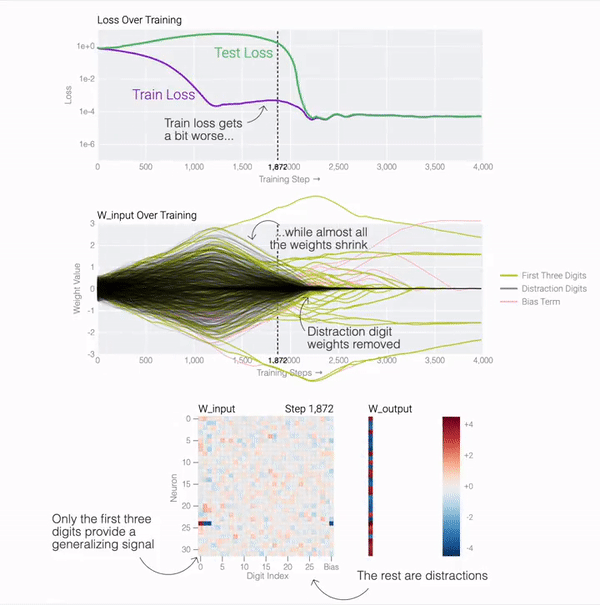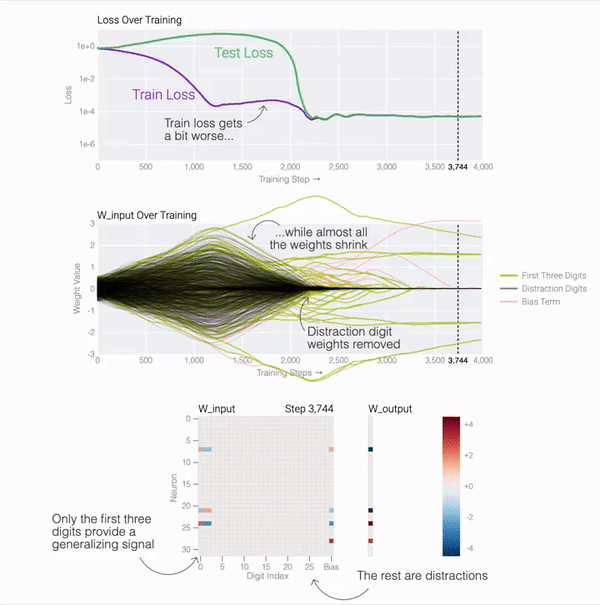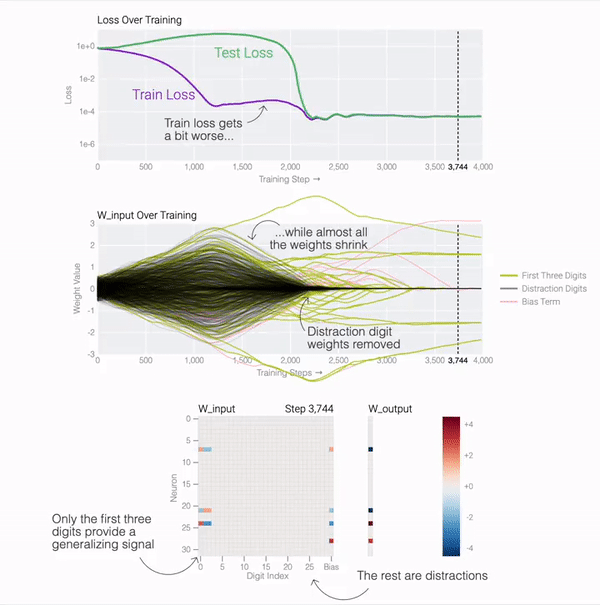
通過 01 序列問題這個簡單的示例,我們可以更容易地理解為什么會發生這種情況。原因就是模型在訓練期間會做兩件事:最小化損失 和權重衰減。在模型泛化之前,訓練損失實際上會略有增加,因為它交換了與輸出正確標簽相關的損失,以獲得較低的權重。
 圖片
圖片
測試損失的急劇下降使得模型看起來像是突然泛化,但如果查看模型在訓練過程中的權重,大多數模型都會在兩個解之間平滑地插值。當與后續分散注意力的數字相連的最后一個權重通過權重衰減被修剪時,快速泛化就會發生。
「領悟」現象是什么時候發生的?
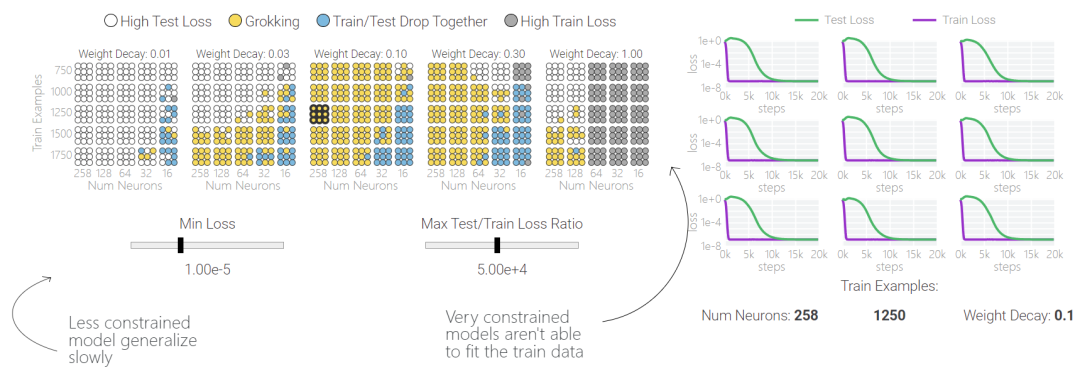
值得注意的是,「領悟(grokking)」是一種偶然現象 —— 如果模型大小、權重衰減、數據大小和其他超參數不合適,「領悟」現象就會消失。如果權重衰減太少,模型就會對訓練數據過渡擬合。如果權重衰減過多,模型將無法學到任何東西。
下面,該研究使用不同的超參數針對 1 和 0 任務訓練了 1000 多個模型。訓練過程充滿噪音,因此針對每組超參數訓練了九個模型。表明只有兩類模型出現「領悟」現象,藍色和黃色。
 圖片
圖片
具有五個神經元的模塊化加法
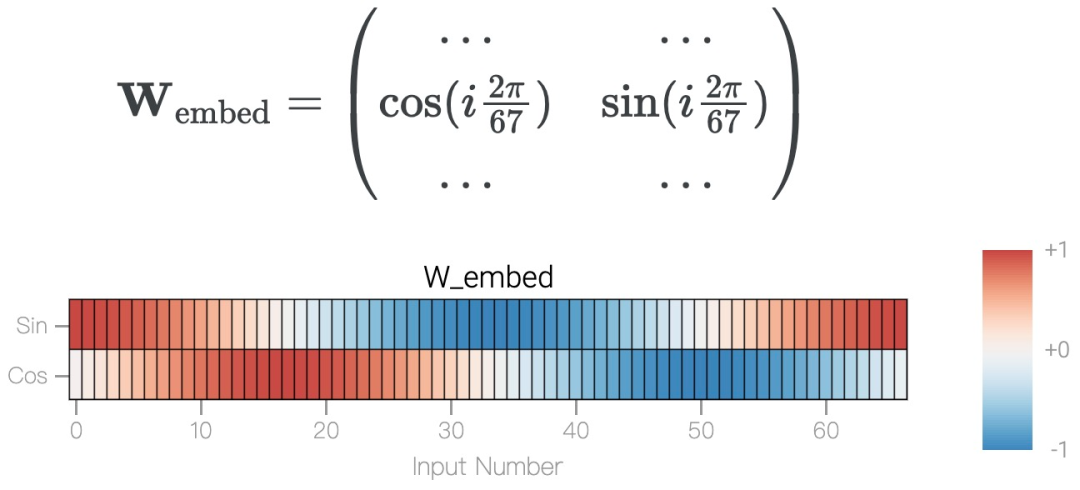
模加法 a+b mod 67 是周期性的,如果總和超過 67,則答案會產生環繞現象,可以用一個圓來表示。為了簡化問題,該研究構建了一個嵌入矩陣,使用 cos? 和 sin? 將 a 和 b 放置在圓上,表示為如下形式。
 圖片
圖片
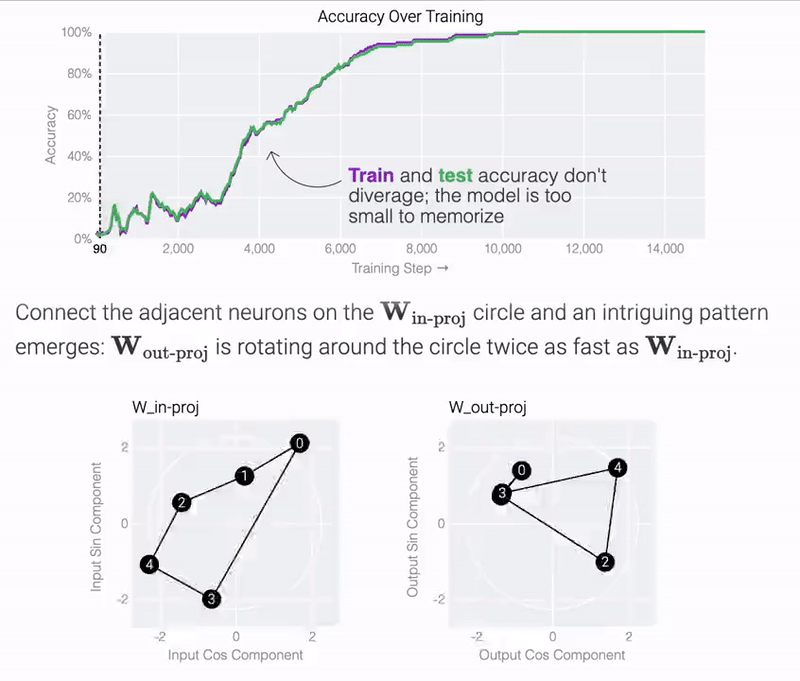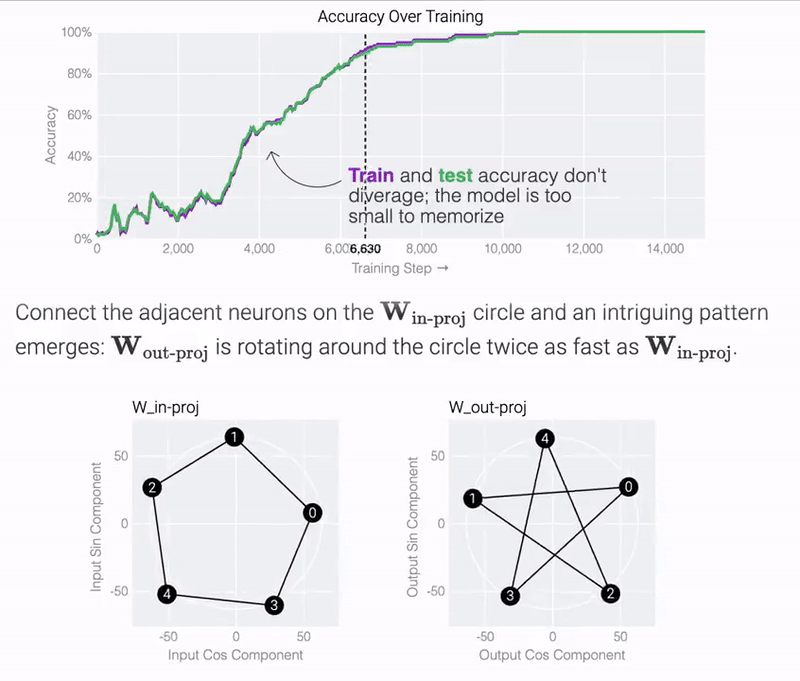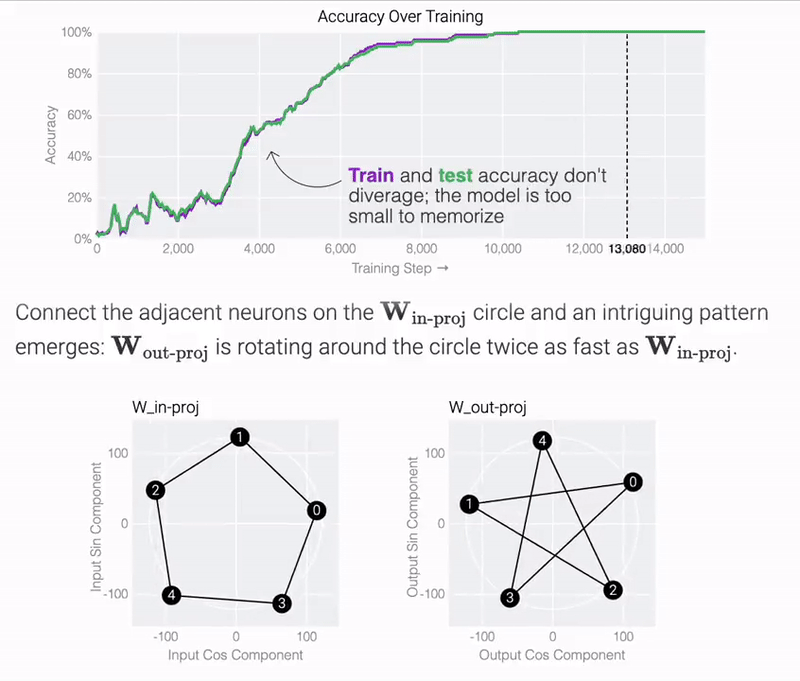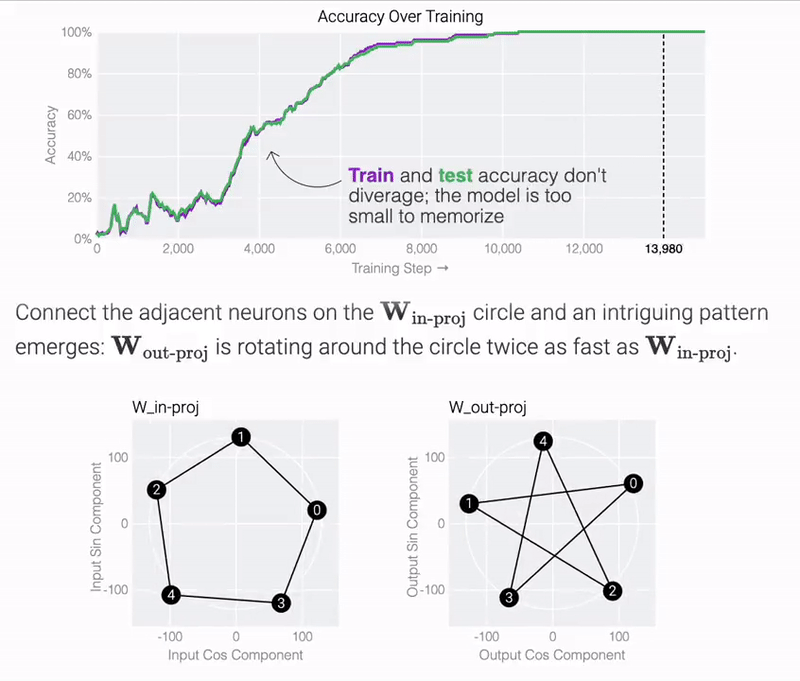
結果表明,模型僅用 5 個神經元就可以完美準確地找到解決方案:
 圖片
圖片
觀察經過訓練的參數,研究團隊發現所有神經元都收斂到大致相等的范數。如果直接繪制它們的 cos? 和 sin? 分量,它們基本上均勻分布在一個圓上。
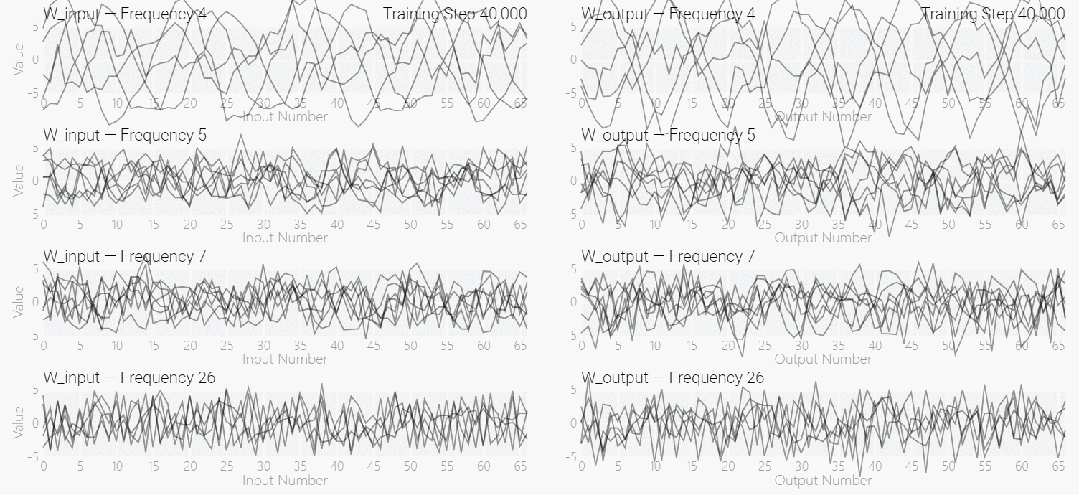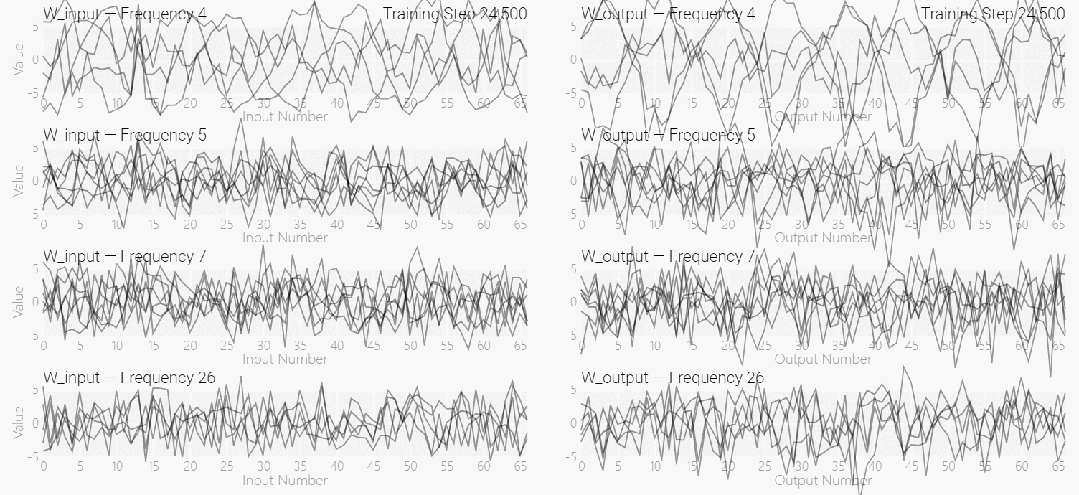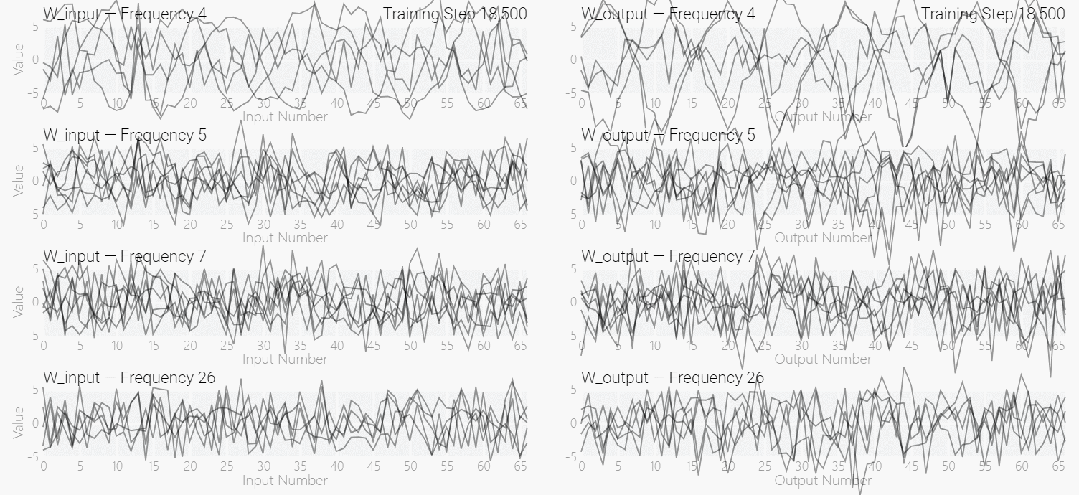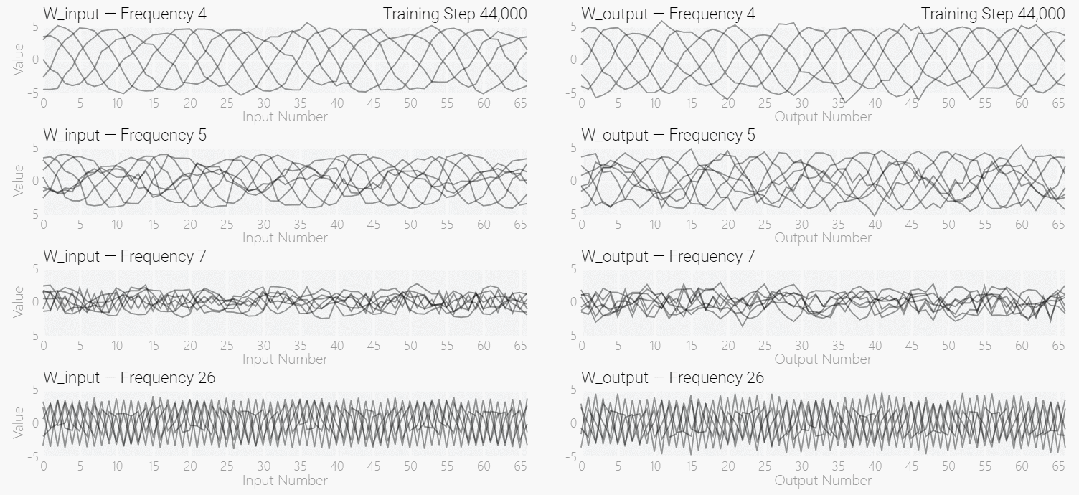
接下來是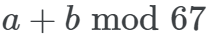 ,它是從頭開始訓練的,沒有內置周期性,這個模型有很多不同的頻率。
,它是從頭開始訓練的,沒有內置周期性,這個模型有很多不同的頻率。
 圖片
圖片
 圖片
圖片
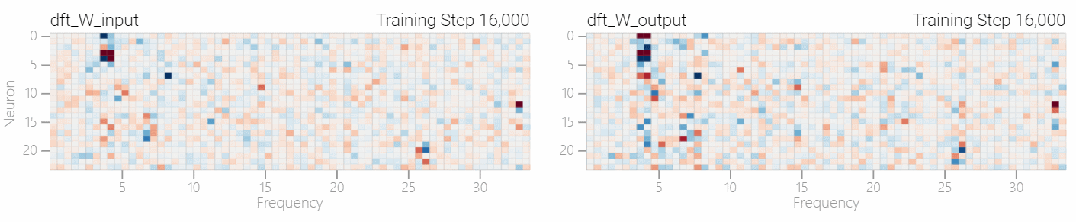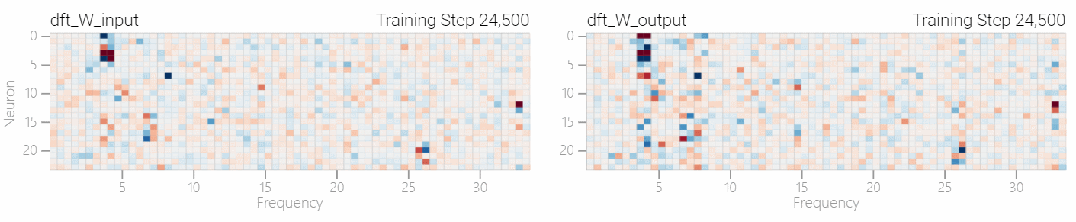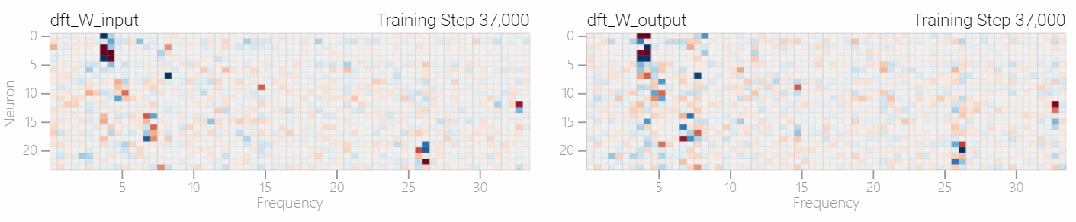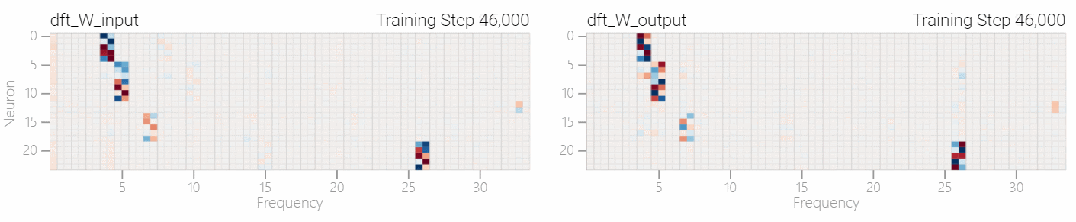
該研究使用離散傅立葉變換 (DFT) 分離出頻率。就像在 1 和 0 任務中一樣,只有幾個權重起到關鍵作用:
 圖片
圖片
下圖表明,在不同的頻率,模型也能實現「領悟」:
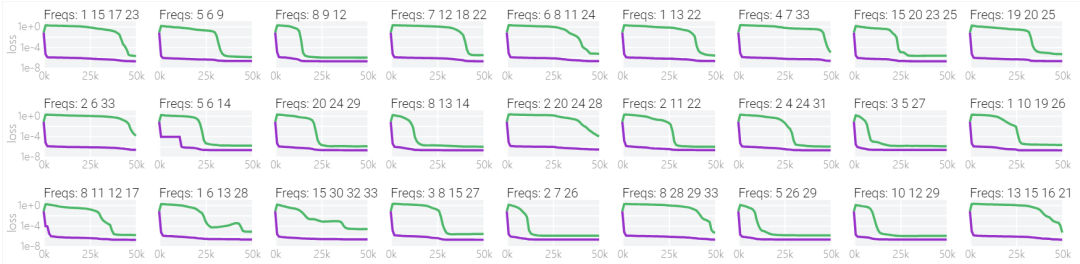 圖片
圖片
開放問題
現在,雖然我們對單層 MLP 解決模加法的機制及其在訓練過程中出現的原因有了扎實的了解,但在記憶和泛化方面仍有許多有趣的開放性問題。
哪種模型的約束效果更好呢?
從廣義上講,權重衰減的確可以引導各種模型避免記憶訓練數據。其他有助于避免過擬合的技術包括 dropout、縮小模型,甚至數值不穩定的優化算法。這些方法以復雜的非線性方式相互作用,因此很難先驗地預測哪種方法最終會誘導泛化。
此外,不同的超參數也會使改進不那么突然。
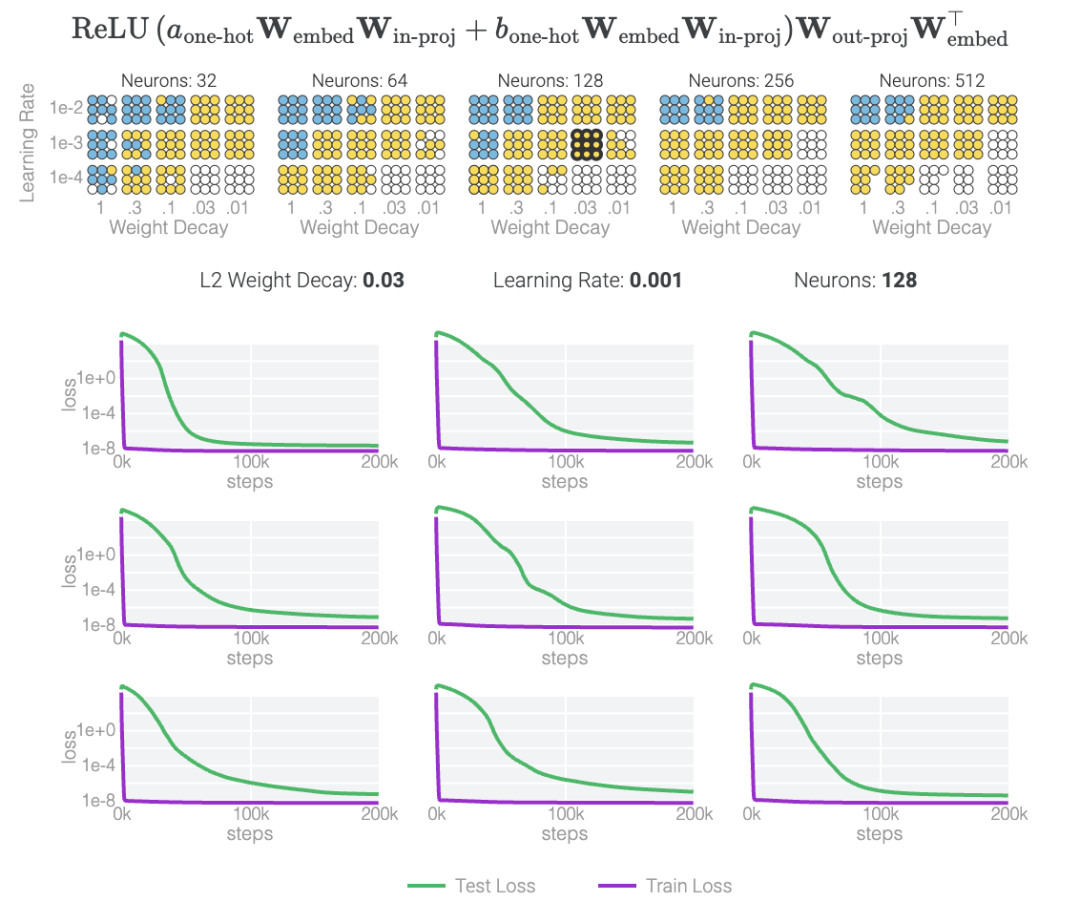 圖片
圖片
為什么記憶比泛化更容易?
有一種理論認為:記憶訓練集的方法可能比泛化解法多得多。因此,從統計學上講,記憶應該更有可能首先發生,尤其是在沒有正則化或正則化很少的情況中。正則化技術(如權重衰減)會優先考慮某些解決方案,例如,優先考慮 「稀疏 」解決方案,而不是 「密集 」解決方案。
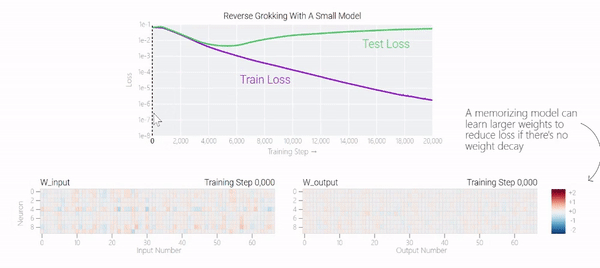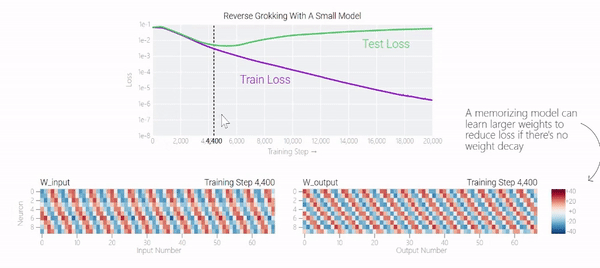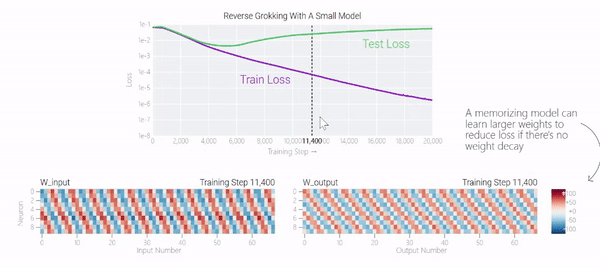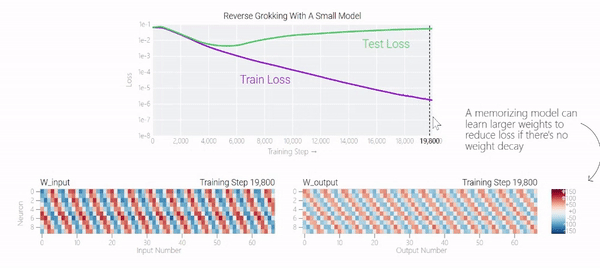
研究表明,泛化與結構良好的表征有關。然而,這不是必要條件;在求解模加法時,一些沒有對稱輸入的 MLP 變體學習到的 「循環 」表征較少。研究團隊還發現,結構良好的表征并不是泛化的充分條件。這個小模型(訓練時沒有權重衰減)開始泛化,然后轉為使用周期性嵌入的記憶。
在下圖中可以看到,如果沒有權重衰減,記憶模型可以學習更大的權重來減少損失。
 圖片
圖片
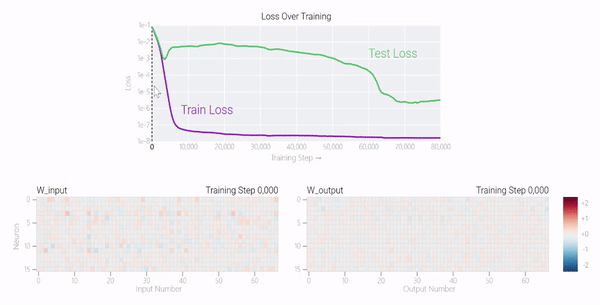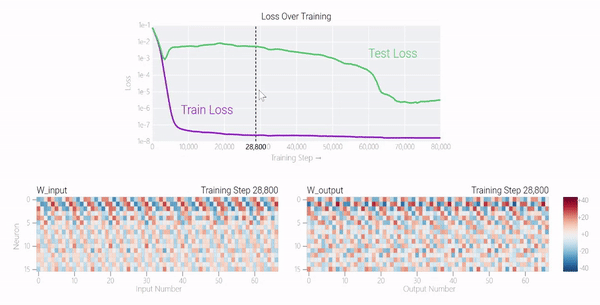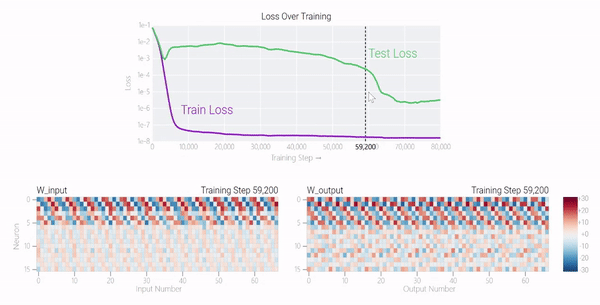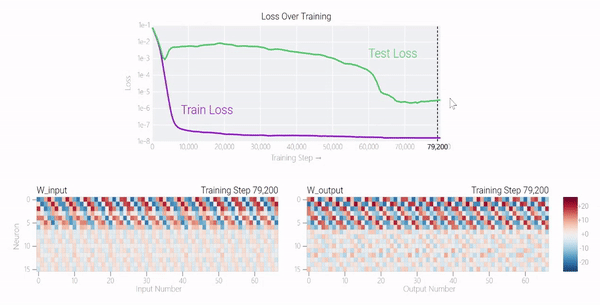
甚至可以找到模型開始泛化的超參數,然后切換到記憶,然后切換回泛化。
 圖片
圖片
較大的模型呢?
理解模加法的解決方案并非易事。我們有希望理解更大的模型嗎?在這條路上可能需要:
- 訓練更簡單的模型,具有更多的歸納偏差和更少的運動部件。
- 使用它們來解釋更大模型如何工作的費解部分。
- 按需重復。
研究團隊相信,這可能是一種更好地有效理解大型模型的的方法,此外,隨著時間的推移,這種機制化的可解釋性方法可能有助于識別模式,從而使神經網絡所學算法的揭示變得容易甚至自動化。
更多詳細內容請閱讀原文。
原文鏈接:https://pair.withgoogle.com/explorables/grokking/











































