Transformer模型是否能夠超越預訓練數據范圍，泛化出新的認知和能力，一直是學界爭議已久的問題。

最近谷歌DeepMind的3位研究研究人員認為，要求模型在超出預訓練數據范圍之外泛化出解決新問題的能力，幾乎是不可能的。

LLM的終局就是人類智慧總和？

論文地址：https://arxiv.org/abs/2311.00871

Jim Fan轉發論文后評論說，這明確說明了訓練數據對于模型性能的重要性，所以數據質量對于LLM來說實在是太重要了。

研究人員在論文中專注于研究預訓練過程的一個特定方面——預訓練中使用的數據——并研究它如何影響最終Transformer模型的少樣本學習能力。

研究人員使用一組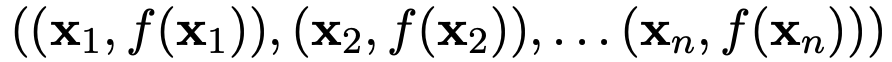來作為輸入和標簽，  來對新輸入的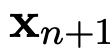的標簽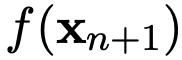進行預測。要訓練模型做出這樣的預測，需要在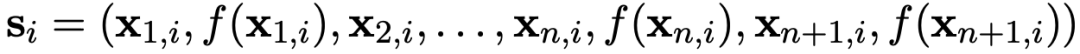形式的許多序列上擬合模型。

研究人員使用包含多種不同函數類別的混合對Transformer模型進行預訓練，以便在上下文中學習，并展示了所表現出的模型選擇行為（Model Selection Phenomena）。

他們還研究了預訓練Transformer模型在與預訓練數據中的函數類別 「不一致 （out-of-distribution）」的函數上的情境學習行為。

通過這種方式，研究人員研究了預訓練數據組成與Transformer模型對相關任務進行少量學習的能力之間的相互作用和影響后發現：

1. 在所研究的機制中，有明確的證據表明，模型在上下文學習過程中可以在預訓練的函數類別中進行模型選擇，而且幾乎不需要額外的統計成本。

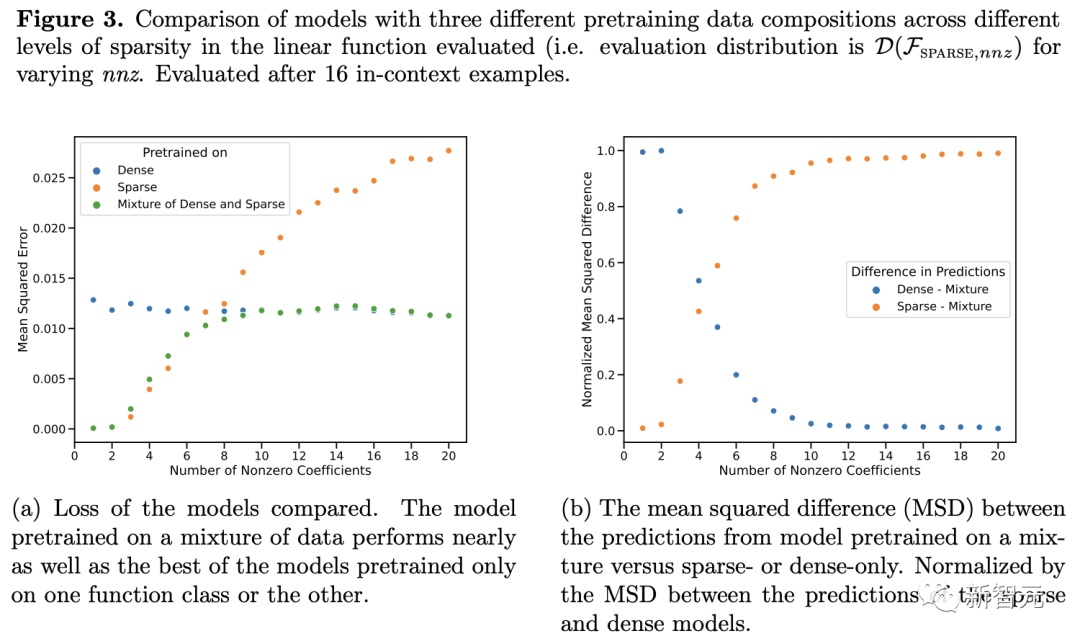
預訓練數據中各個稀疏程度的線性函數都被很好地覆蓋的情況下，Transformer可以進行近似最優的預測。

2. 但幾乎沒有證據表明，模型的上下文學習行為能夠超出其預訓練數據的范圍。

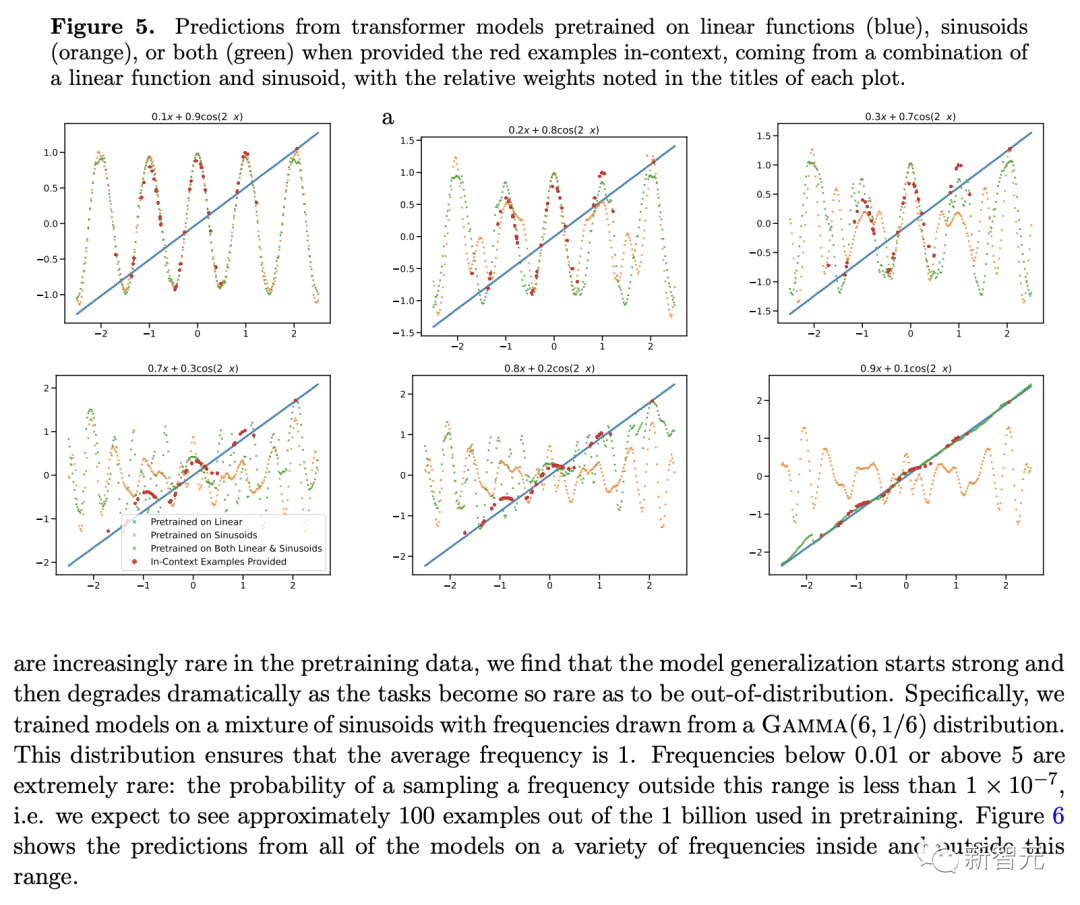
當組合函數主要來自一個函數類時，預測合理。當兩個類同時顯著貢獻時，預測失效。

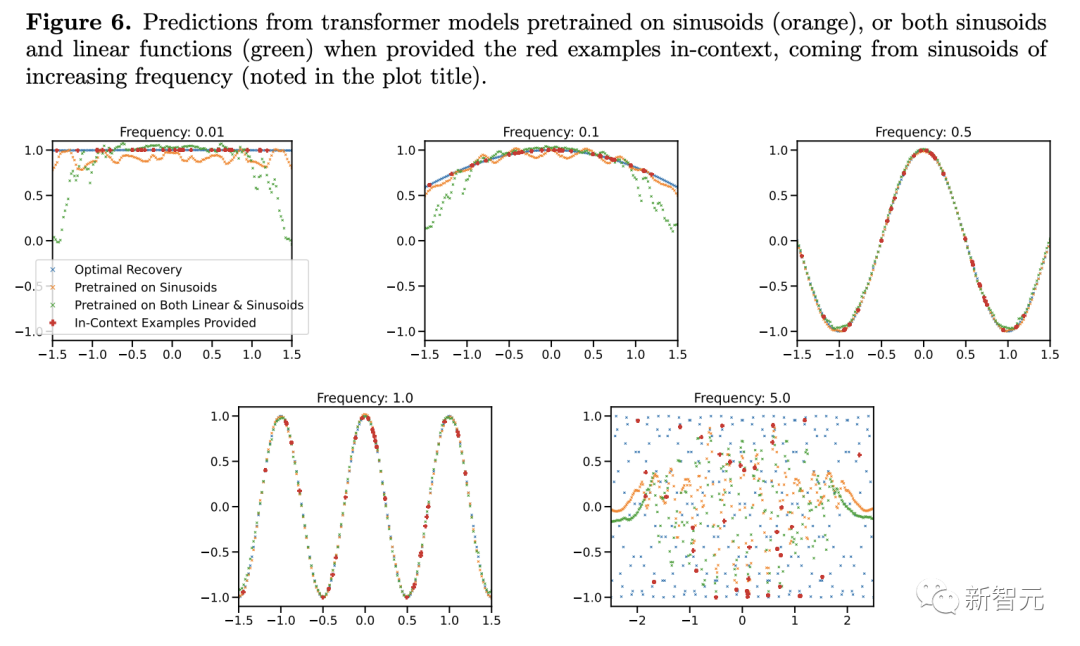
對于預訓練數據中極為罕見的高低頻正弦函數，模型的泛化會失敗。

研究過程細節

首先，為了避免產生誤解，這里先聲明本實驗所采用的模型：類似于GPT-2，包含12層，256維嵌入空間。

之前提到了文章使用不同函數混合的方法進行研究，

那么我們不禁要問：「當提供支持預訓練混合的上下文示例時，模型如何在不同的函數類之間進行選擇？」

之前的研究表明，在線性函數上預訓練的Transformer在對新的線性函數進行上下文學習時表現幾乎最優。

于是研究人員采用兩個線性模型來進行研究：一個在密集線性函數上訓練（其中線性模型的所有系數都是非零的），另一個在稀疏線性函數上訓練（假設20個系數中只有2個是非零的）。

每個模型分別對新的密集線性函數和稀疏線性函數執行相應的線性回歸和套索回歸（Lasso）。此外，還將這兩個模型與在稀疏線性函數和密集線性函數的混合上預訓練的模型進行了比較。

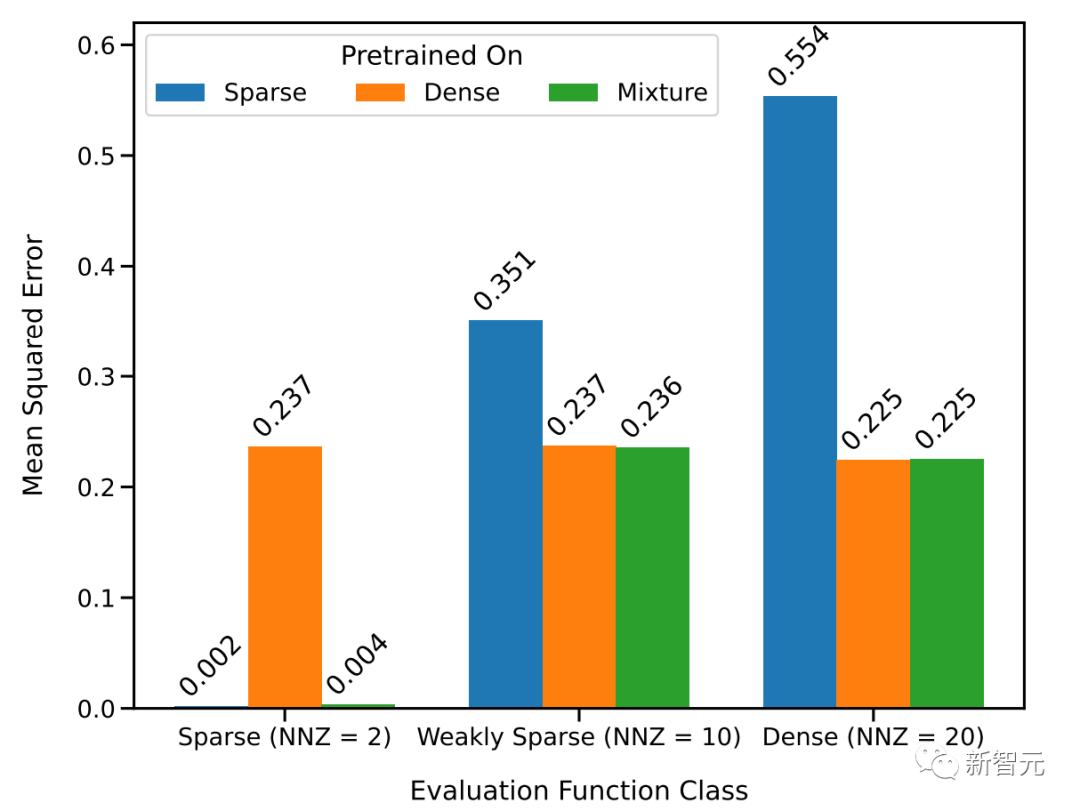
上圖顯示，在以D（F） = 0.5*D（F1）+0.5*D（F2）的比例混合兩個函數的情況下，新的函數在上下文學習中的表現與僅在一個函數類上預訓練的模型相似。

而在新的混合函數上預訓練的模型與前人研究中所展示的模型（理論上最優）相似，因此可以推斷該模型也幾乎是最優的。

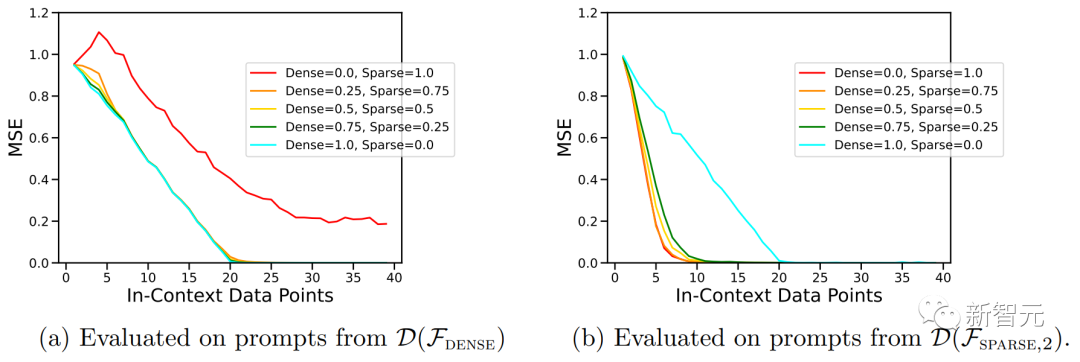
上圖中的ICL學習曲線向我們表明，這種上下文模型選擇能力相對于提供的上下文示例數量相對一致。

我們還可以看到，與純粹基于該函數類預訓練模型相比，對于給定函數類，這種使用權重來進行預訓練數據混合的ICL學習曲線幾乎與最佳基線樣本復雜度相匹配。

上圖還表明，Transformer模型ICL泛化存在分布不均。盡管密集線性類和稀疏線性類都是線性函數，但我們可以看到上圖（a）中的紅色曲線性能較差，而相應的，圖（b）中的藍色曲線性能較差。

這表明該模型能夠執行模型選擇，以選擇是否僅使用預訓練組合中一個基函數類或另一個基函數類的知識進行預測。

事實上，當上下文中提供的示例來自非常稀疏或非常密集的函數時，預測幾乎與分別在僅稀疏或僅密集數據上預訓練的模型所做的預測相同。

模型的局限性 

之前的實驗展示了混合預訓練數據的情況，下面我們來探索一些明確脫離所有預訓練數據的函數。

作者在這里研究了模型沿兩個軸的ICL泛化能力：從未見過的函數，以及函數的極端版本（頻率比預訓練中通常看到的頻率高得多或低得多的正弦曲線）上的性能。

在這兩種情況下，研究人員幾乎沒有發現分布外泛化的證據。

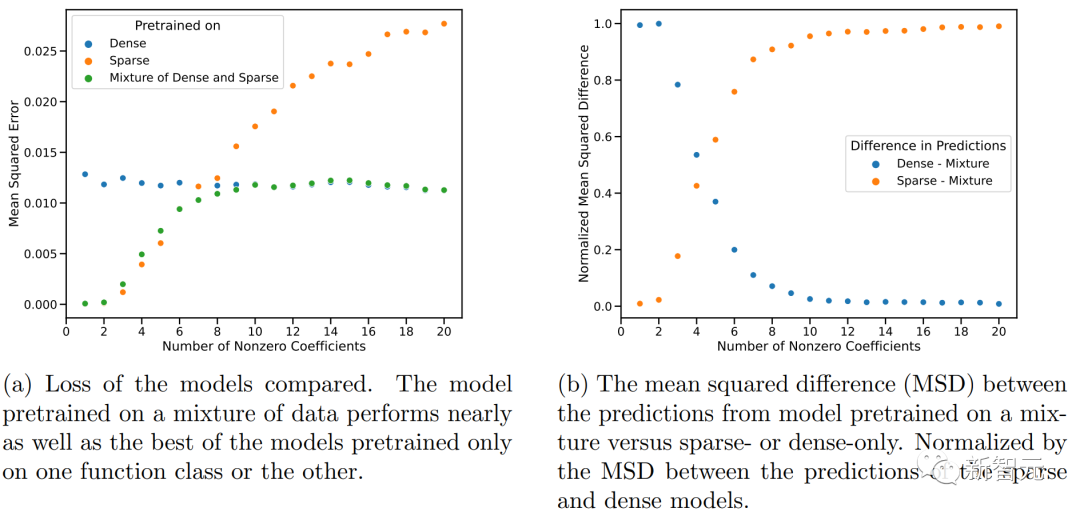
上圖顯示，Transformer在中等稀疏度水平（nnz=3到7）下的預測與預訓練時提供的任何函數類的任何預測都不相似，而是介于兩者之間。

因此，可以假設該模型具有一些歸納偏差，可以組合預訓練的函數類。

但是，人們可能會懷疑該模型可以從預訓練期間看到的函數組合中產生預測。

所以作者在具有明顯不相交的函數類的背景下檢驗這一假設，研究了對線性函數、正弦函數和兩者的凸組合執行 ICL 的能力。

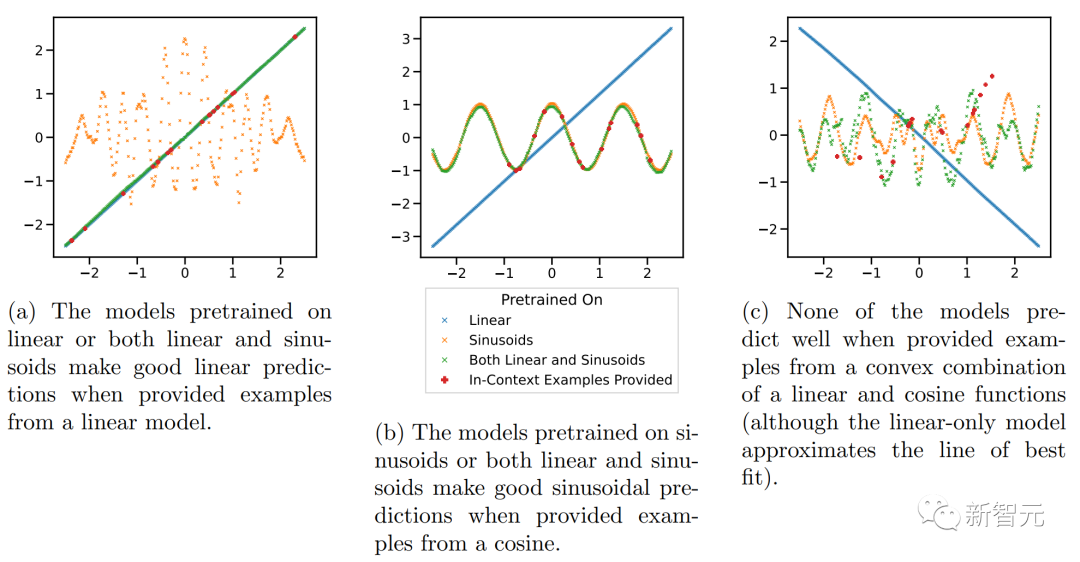
上圖顯示，雖然模型在線性函數和正弦曲線的混合上進行預訓練（即D（F） = 0.5*D（F1）+0.5*D（F2））能夠分別對這兩個函數中的任何一個做出良好的預測，但它無法擬合兩者的凸組合的函數。

然而，我們仍然可以假設：當上下文中的示例接近在預訓練中學習的函數類時，模型能夠選擇用于預測的最佳函數類。

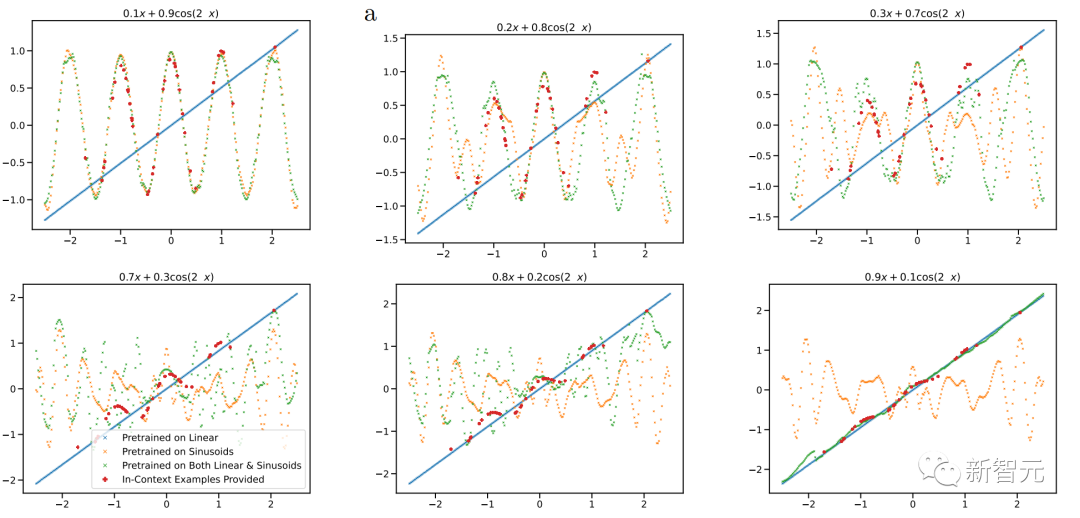
在圖 5 中，研究人員掃描了凸組合中線性函數和正弦波的相對權重。在這里，研究人員觀察到，當組合函數主要來自一個函數類或另一個函數類時——即通過預訓練期間學習的函數類很好地近似——上下文預測是合理的。

但是，當這兩個函數對凸組合有顯著貢獻時，模型會做出不穩定的預測，而上下文示例并不能很好地證明其合理性。這表明模型的模型選擇能力受到與預訓練數據的接近程度的限制，并表明功能空間的廣泛覆蓋對于廣義的上下文學習能力至關重要。

前面的凸組合是專門構造的，因此模型在預訓練中從未見過類似的函數。

網友熱議

面對文章的結論，Jim Fan給出了略帶嘲諷的評價：

「本文相當于：嘗試只在狗和貓的數據集上訓練ViT。使用100B狗/貓圖像和1T 參數！現在看看它是否能識別飛機——令人驚訝的是，它不能！」

但是有好事的網友把這個事請拿去問了下ChatGPT，它自己卻回答說，自己可以超越訓練數據輸出新的內容。

而網友對于Transformer的這個局限還是很寬容的，畢竟，人類也不行。

AIGC的火熱引起人們對于模型能力的廣泛研究，對于我們無法完全了解的、卻廣泛應用于社會和生活中的「 人工智能 」，知道它的邊界在哪里也很重要。