棧和括號匹配難題,一文徹底搞懂

什么是棧
棧在我們?nèi)粘>幋a中遇到的非常多,很多人對棧的接觸可能僅僅局限在 遞歸使用的棧 和 StackOverflowException,棧是一種后進先出的數(shù)據(jù)結(jié)構(gòu)(可以想象生化金字塔的牢房和生化角斗場的狗洞)。
棧(stack)是一種運算受限的線性數(shù)據(jù)結(jié)構(gòu),它具有以下特點:
1. 運算受限: 棧限定僅在表尾進行插入和刪除操作,這一端被稱為棧頂,而另一端稱為棧底。這限制了對棧的操作,只能按照后進先出(LIFO,Last-In-First-Out)的原則進行插入和刪除操作。插入操作又稱為進棧、入棧或壓棧,它將新元素放到棧頂,使之成為新的棧頂元素;刪除操作又稱為出棧或退棧,它將棧頂元素刪除,使其相鄰的元素成為新的棧頂元素。
2. 線性表: 棧也是一種線性表,它表示數(shù)據(jù)元素之間的邏輯關(guān)系是線性的。雖然具體實現(xiàn)可以使用數(shù)組或鏈表等不同的物理存儲結(jié)構(gòu),但邏輯上各個元素之間是相鄰的,操作也是按照順序進行的。
3. 棧頂和棧底: 棧的邏輯結(jié)構(gòu)中有棧頂和棧底的概念。棧頂表示可以進行插入和刪除操作的一端,通常與數(shù)組的末尾或鏈表的頭部有關(guān)。棧底則是相對的另一端,用于限制操作的另一端。
4. 棧的應用: 棧在計算機科學和編程中有廣泛的應用,例如程序執(zhí)行調(diào)用堆棧、四則運算表達式求值、非遞歸算法實現(xiàn)、括號匹配問題、瀏覽器歷史、內(nèi)存分配、任務管理等的解決。掌握棧是非常重要的,它是必須了解的數(shù)據(jù)結(jié)構(gòu)之一。
棧可以使用數(shù)組或鏈表來實現(xiàn),選擇合適的實現(xiàn)方式取決于具體的應用場景和性能需求。數(shù)組實現(xiàn)的棧通常更適合于需要固定大小的棧(當然也可以進行擴容),而鏈表實現(xiàn)的棧可以動態(tài)擴展,適用于不確定大小的棧。在棧的操作中,棧頂元素是非常關(guān)鍵的,因為它在插入和刪除操作中起著重要作用。
總之,棧是一個非常有用的數(shù)據(jù)結(jié)構(gòu),它在計算機科學中扮演著重要的角色,了解它的特性和應用對于編程和算法設(shè)計至關(guān)重要。
對于一個棧的接口,我們簡易定義如下:
public interface Stack<T> {
void push(T item); // 壓棧
T pop(); // 彈棧
T peek(); // 獲取棧頂元素
boolean isEmpty(); // 判斷棧是否為空
int size(); // 返回棧的大小
}數(shù)組實現(xiàn)
數(shù)組實現(xiàn)的棧用的比較多,我們經(jīng)常刷題也會用數(shù)組去實現(xiàn)一個簡單的棧去解決簡單的問題。
結(jié)構(gòu)設(shè)計
對于數(shù)組來說,我們模擬棧的過程很簡單,因為棧是后進先出,我們很容易在數(shù)組的末尾進行插入和刪除。所以我們選定末尾為棧頂。所以對于一個棧所需要的基礎(chǔ)元素是 一個array[]數(shù)組和一個size表示大小,還需要一個負載因子表示數(shù)組的大小。
push入棧操作
- 如果數(shù)組滿了,需要擴容
- size位置賦值,array[size++] = data;
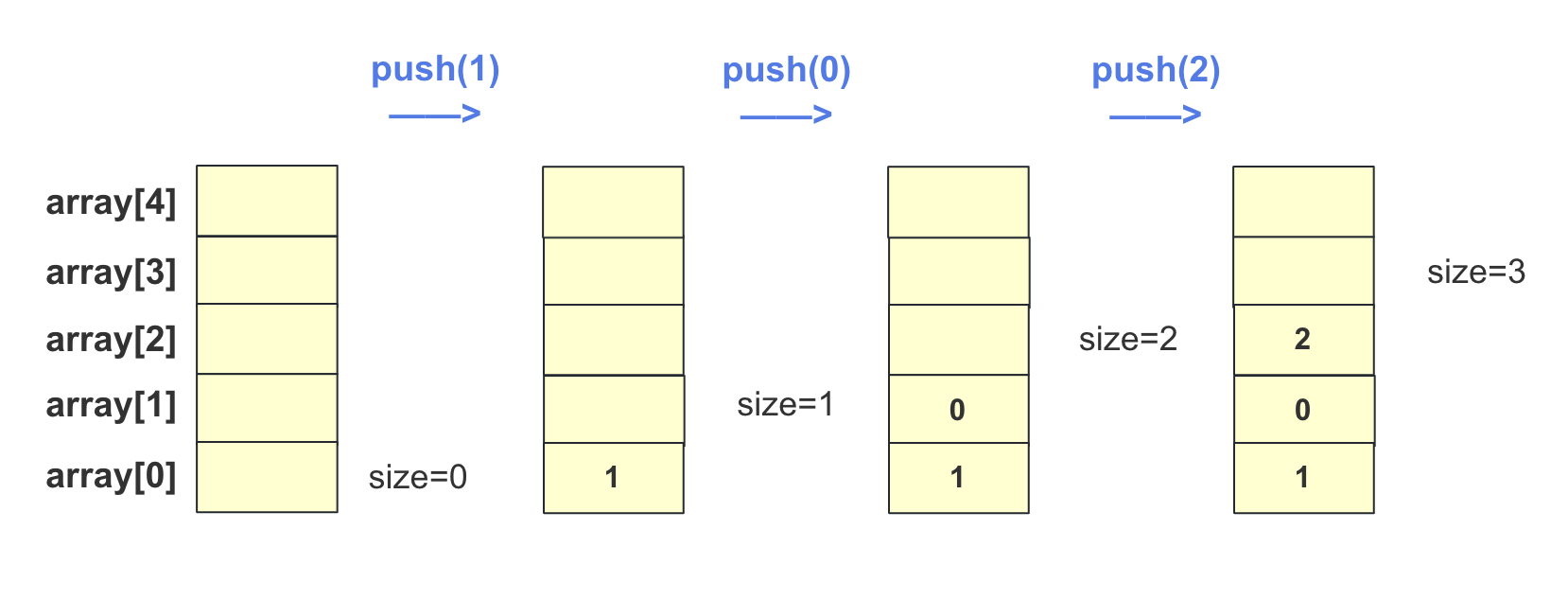
pop彈出棧并返回首位
- 如果棧不為空,可以彈出。return array[--size];
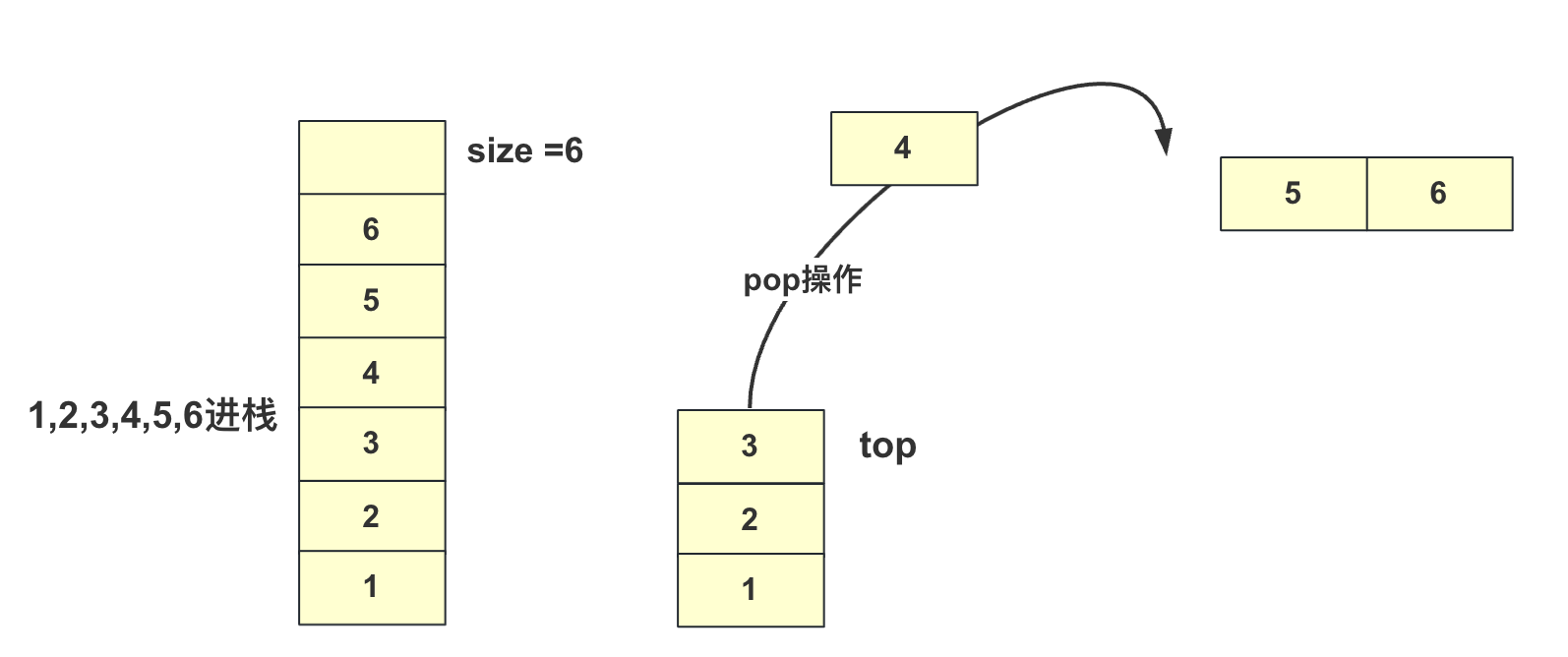
如下圖,當棧中還剩1,2,3,4執(zhí)行pop操作,棧頂變?yōu)?的位置并且返回4
peek返回棧頂
- peek操作時返回棧頂不彈出,所以棧不為空時候return data[size-1]即可。
數(shù)組實現(xiàn):
import java.util.EmptyStackException;
public class SeqStack<T> implements Stack<T> {
private T array[];
private int size;
private static final int DEFAULT_CAPACITY = 10;
public SeqStack() {
this.size = 0;
array = (T[]) new Object[DEFAULT_CAPACITY];
}
@Override
public void push(T data) {
if (size == array.length) {
// 如果數(shù)組已滿,擴展數(shù)組
resizeArray();
}
array[size++] = data;
}
@Override
public T pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
// 下面可以寫成 return array[--size];
T data = array[size - 1];
size--;
return data;
}
@Override
public T peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return array[size - 1];
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public int size() {
return size;
}
private void resizeArray() {
int newCapacity = (int) (array.length * 2);
T[] newArray = (T[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newArray[i] = array[i];
}
array = newArray;
}
}鏈表實現(xiàn)
棧可以使用數(shù)組或鏈表來實現(xiàn),兩種思路如下:
鏈表尾部作為棧頂: 在數(shù)組實現(xiàn)中,棧的操作是在尾部進行插入和刪除。鏈表中即使使用尾指針可以提高尾部插入效率,但刪除操作仍然需要查找前驅(qū)節(jié)點。要實現(xiàn)高效的刪除操作,需要使用雙向鏈表,這增加了整個結(jié)構(gòu)的復雜性。
鏈表頭部作為棧頂: 在這種實現(xiàn)中,棧的設(shè)計不帶頭節(jié)點的單鏈表(不需要啞結(jié)點),所有操作都在鏈表的頭部進行。頭部插入刪除都很方便效率比較高,編寫代碼也很簡單。
基礎(chǔ)結(jié)構(gòu)
public class LinkedStack<T> implements Stack<T> {
private Node<T> top;
private int size;
public LinkedStack() {
top = null;
size = 0;
}
private static class Node<T> {
T data;
Node<T> next;
public Node(T data) {
this.data = data;
this.next = null;
}
}
//其他方法
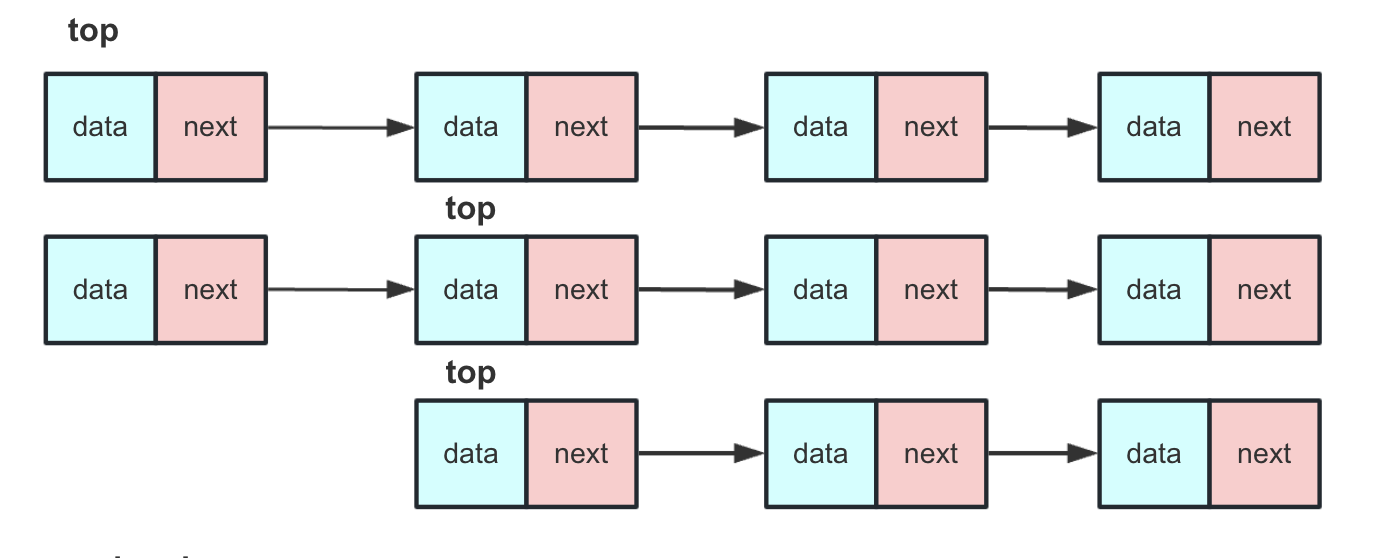
}push入棧
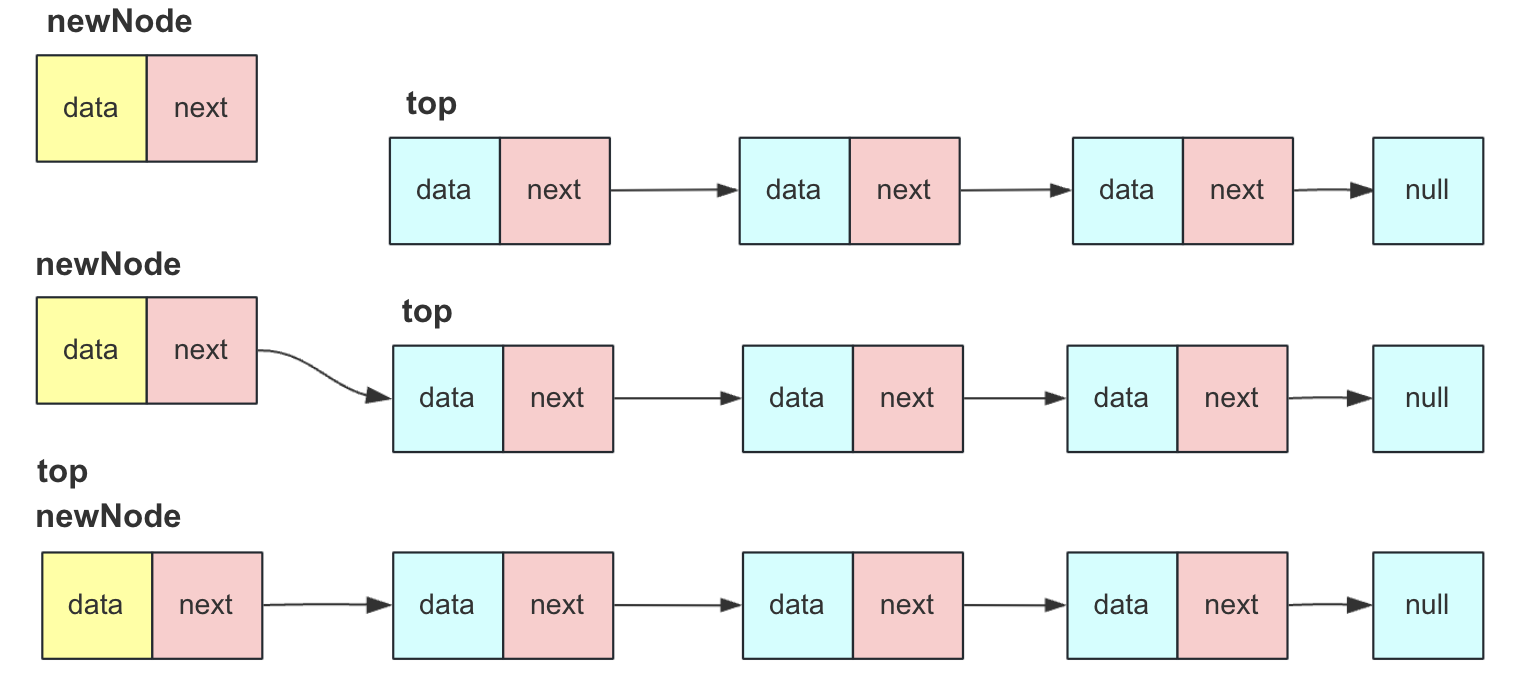
與不帶頭結(jié)點單鏈表頭插入一致:
- 創(chuàng)建新節(jié)點
- 新節(jié)點的next指向棧頂節(jié)點top
- 棧頂節(jié)點top指向新節(jié)點,表示這個節(jié)點為新的棧頂節(jié)點
- size++
部分操作流程如下圖
pop彈出
與不帶頭結(jié)點單鏈表頭插入一致:
- 判斷是否為空
- 記錄頭結(jié)點top的值data
- 頭結(jié)點top指向top.next
- size--,返回前面記錄的值data
部分操作流程如下圖:
peek返回棧頂
不為空的時候返回 top.data即可。
鏈表實現(xiàn):
import java.util.EmptyStackException;
public class LinkedStack<T> implements Stack<T> {
private Node<T> top;
private int size;
public LinkedStack() {
top = null;
size = 0;
}
private static class Node<T> {
T data;
Node<T> next;
public Node(T data) {
this.data = data;
this.next = null;
}
}
@Override
public void push(T item) {
Node<T> newNode = new Node<>(item);
newNode.next = top;
top = newNode;
size++;
}
@Override
public T pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
T data = top.data;
top = top.next;
size--;
return data;
}
@Override
public T peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return top.data;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public int size() {
return size;
}
}棧能這么玩
既然上面詳細講解設(shè)計棧,這里來兩道棧非常經(jīng)典非常經(jīng)典的例題(非常高頻,很容易忘,又很重要,普通問題就不放的)。
力扣20有效的括號:
題意:給定一個只包括 '(',')','{','}','[',']' 的字符串,判斷字符串是否有效。
有效字符串需滿足:
左括號必須用相同類型的右括號閉合。
左括號必須以正確的順序閉合。
注意空字符串可被認為是有效字符串。
示例 :
輸入: "()[]{}"
輸出: true
示例 :
輸入: "([)]"
輸出: false
括號類的問題是經(jīng)典棧類問題,肯定要想到用棧處理。判斷一個字符串滿不滿足一個有效的字符串,就要看它是不是都能組成對。
從單個括號對來說,((,))都是不滿足的,只有()才可滿足,即一左一右。
從多個括號對來說 {[(字符串還可接受任意無限(,[,{的括號。但是如果向左的括號只能先接收)括號(變成{[)。
從上面可以看作一種相消除的思想。例如(({[()()]}))字符串遍歷時候可以這樣處理:
- (({[(下一個)消掉成(({[
- (({[(下一個)消掉成(({[
- (({[下一個]消掉成(({
- (({下一個}消掉成((
- ((下一個)消掉成(
- (下一個)消掉成 這樣就滿足題意
每次操作的時候都判斷剩余有效括號最頂部那個括號是否能夠和遍歷的相消除,這個過程利用棧判斷當前是加入棧還是消除頂部,到最后如果棧為空說明滿足,否則不滿足,當然具體括號要對應,具體實現(xiàn)代碼為:
public boolean isValid(String s) {
Stack<Character> stack = new LinkedStack<Character>();
for (int i = 0; i < s.length(); i++) {
char te = s.charAt(i);
if (te == ']') {
if (!stack.isEmpty() && stack.pop() == '[')
continue;
else {
return false;
}
} else if (te == '}') {
if (!stack.isEmpty() && stack.pop() == '{')
continue;
else {
return false;
}
} else if (te == ')') {
if (!stack.isEmpty() && stack.pop() == '(') {
continue;
} else {
return false;
}
} else {
stack.push(te);
}
}
return stack.isEmpty();
}當然,JDK自帶的棧用起來不快,可以用數(shù)組優(yōu)化:
public boolean isValid(String s) {
char a[] = new char[s.length()];
int index = -1;
for (int i = 0; i < s.length(); i++) {
char te = s.charAt(i);
if (te == ']') {
if (index >= 0 && a[index] == '[')
index--;
else {
return false;
}
} else if (te == '}') {
if (index >= 0 && a[index] == '{')
index--;
else {
return false;
}
} else if (te == ')') {
if (index >= 0 && a[index] == '(')
index--;
else {
return false;
}
} else {
a[++index] = te;
}
}
return index == -1;
}力扣32最長有效括號(困難)
題目描述:給定一個只包含 '(' 和 ')' 的字符串,找出最長的包含有效括號的子串的長度。
示例 :
輸入: "(()"
輸出: 2
解釋: 最長有效括號子串為 "()"
示例 :
輸入: ")()())"
輸出: 4
解釋: 最長有效括號子串為 "()()"
方案一暴力
這種題核心思想就是使用棧模擬。本題的話更簡單一點因為只有(和)兩種括號,使用暴力的時候就可以循環(huán)每次找到最長的有效括號。而括號匹配的時候可以直接終止的情況是)右括號多出無法匹配。
例如())(到第三個不可能和前面相連。如果來(只需要期待后面能夠來),一個)可以和一個(組成一對,消除棧中的一個(。
當然,在具體的實現(xiàn)上,我們用數(shù)組模擬棧,實現(xiàn)代碼為:
public int longestValidParentheses(String s) {
char str[] = s.toCharArray();//字符數(shù)組
int max = 0;
for (int i = 0; i < str.length - 1; i++) {
int index = -1;
if (max >= str.length - i)
break;
for (int j = i; j < str.length; j++) {
if (str[j] == '(') {
index++;
} else {
if (index < 0) {
i = j;
break;
} else {
index--;
}
}
if (index == -1 && (j - i + 1 > max)) {
max = j - i + 1;
}
}
}
return max;
}這個復雜度太高,我們看看如何用棧優(yōu)化。
方案二棧優(yōu)化
如何將這道題從一個O(n^2)的時間復雜度優(yōu)化到O(n)?這其實非常簡單,只需要注意處理的過程。讓我們首先考慮一些可能的最大情況。
- ( ) ) ( ) ( ( ) ( ) ) 最大為后面部分(空格分開)
- ( ) ( ) ( ( ( ) 最大為前面部分
- ( ( ( ( ( ( ) ( ) ( ) ( ) 最大為后面部分
在處理這道題時,我們會注意到不同類型的括號可能會有一些區(qū)別:(:左括號一旦出現(xiàn)那么他就期待一個)進行匹配,但它的后面可能有)并且在這中間有很多其他括號對。
):右擴號有兩種情況:
- 一種是當前已經(jīng)超過左括號前面已經(jīng)不可能連續(xù)了。例如( ) ) ( )第三個括號出現(xiàn)已經(jīng)使得整個串串不可能連續(xù),最大要么在其左面,要么再其右面。 你可以理解其為一種清零初始機制。
- 另一種情況)就是目標棧中存在(可與其進行匹配。匹配之后要疊加到消除后平級的數(shù)量上,并且判斷是否是最大值。(下面會解釋)
在具體實現(xiàn)的思路上,就是使用一個int數(shù)組標記當前層級(棧深)有正確的括號數(shù)量。 模擬一次棧行為從左向右,遇到)太多(當前棧中不存在(進行匹配)就將數(shù)據(jù)清零重新開始。這樣一直到最后。你可以把它看成臺接,遇到(就上一個臺階并清零該新臺階,遇到)就下一個臺階并且把數(shù)量加到下降后的臺階上。具體可以看下面圖片模擬的過程:
( ) ( ( ) ( ) ( ( ) ) )
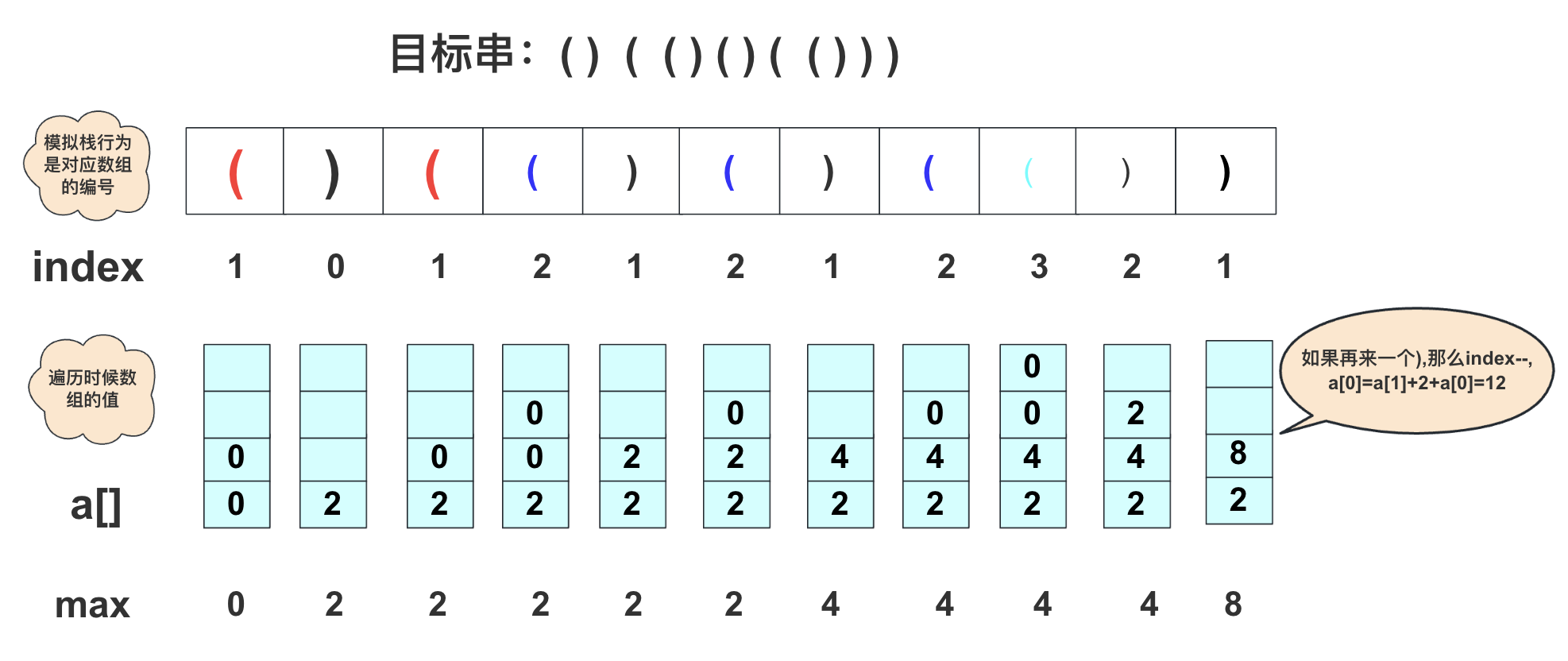
具體實現(xiàn)代碼為:
public static int longestValidParentheses(String s) {
int max = 0;
int value[] = new int[s.length() + 1];
int index = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
index++;
value[index] = 0;
} else {//")"
if (index == 0) {
value[0] = 0;
} else {
value[index - 1] += value[index--] + 2;//疊加
if (value[index] > max)//更新
max = value[index];
}
}
}
return max;
}用棧也可以實現(xiàn),但是效率比數(shù)組略低:
public int longestValidParentheses(String s) {
int maxans = 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {//(將當前的
stack.push(i);
} else {
stack.pop();
if (stack.empty()) {
stack.push(i);
} else {//i-stack.peek就是i是出現(xiàn)的總個數(shù) peek是還沒匹配的個數(shù)
maxans = Math.max(maxans, i - stack.peek());
}
}
}
return maxans;
}總結(jié)
到這里,本文對棧的介紹就結(jié)束了,相信你可以手寫個棧并且可以小試牛刀解決括號匹配問題!當然棧能解決的問題還有很多比如接雨水問題、二叉樹非遞歸遍歷等等,有些重要的還會再總結(jié)。