小羊駝團隊的新研究火了。

他們開發(fā)了一種新的解碼算法，可以讓模型預測100個token數的速度提高1.5-2.3倍，進而加速LLM推理。

比如這是同一個模型（LLaMa-2-Chat 7B）面對同一個用戶提問（蘇格拉底采用了哪些方法來挑戰(zhàn)他那個時代的主流思想？）時輸出回答的速度：

左邊為原算法，耗時18.12s，每秒約35個token；

右邊為該算法，耗時10.4s，每秒約60個token，明顯快了一大截。

簡單來說，這是一種并行解碼算法，名叫“Lookahead Decoding” （前向解碼）。

它主要利用雅可比（Jacobi）迭代法首次打破自回歸解碼中的順序依賴性 （眾所周知，當下大模型基本都是基于自回歸的Transformer）。

由此無需草稿模型（draft model）或數據存儲，就可以減少解碼步驟，加速LLM推理。

目前，作者已給出了與huggingface/transformers兼容的實現，只需幾行代碼，使用者即可輕松增強HF原生生成的性能。

有網友表示：

該方法實在有趣，沒想到在離散設置上效果這么好。

還有人稱，這讓我們離“即時大模型”又近了一步。

具體如何實現？

加速自回歸解碼的重要性

不管是GPT-4還是LLaMA，當下的大模型都是基于自回歸解碼，這種方法下的推理速度其實是非常慢的。

因為每個自回歸解碼步驟一次僅生成一個token。

這樣一來，模型輸出的延遲有多高就取決于回答的長度。

更糟的是，這樣的操作方式還浪費了現代GPU的并行處理能：GPU利用率都很低。

對于聊天機器人來說，當然是延遲越低，響應越快越好（尤其面對長序列答案時）。

此前，有人提出了一種叫做推測解碼的加速自回歸解碼的算法，大致思路是采用猜測和驗證策略，即先讓草稿模型預測幾個潛在的未來token，然后原始LLM去并行驗證。

該方法可以“憑好運氣”減少解碼步驟的數量，從而降低延遲.

但也有不少問題，比如效果受到token接受率的限制，創(chuàng)建準確的草稿模型也麻煩，通常需要額外的訓練和仔細的調整等。

在此，小羊駝團隊提出了一種的新的精確并行解碼算法，即前向解碼來克服這些挑戰(zhàn)。

前向解碼打破順序依賴性

前向解碼之所以可行，是作者們觀察到：

盡管一步解碼多個新token是不可行的，但LLM確實可以并行生成多個不相交的n-grams——它們可能適合生成序列的未來部分。

這可以通過將自回歸解碼視為求解非線性方程，并采用經典的Jacobi迭代法進行并行解碼來實現。

在過程中，我們就讓生成的n-grams被捕獲并隨后進行驗證，如果合適就將其集成到序列中，由此實現在不到n個步驟的時間內生成n個token的操作。

作者介紹，前向解碼之所以能夠“脫穎而出”，主要是因為它：

一不需草稿模型即可運行，簡化了部署。

二是相對于每步 log(FLOPs) 線性減少了解碼步驟數，最終在單個GPU、不同數據集上實現快1.5倍-2.3倍的token數預測。

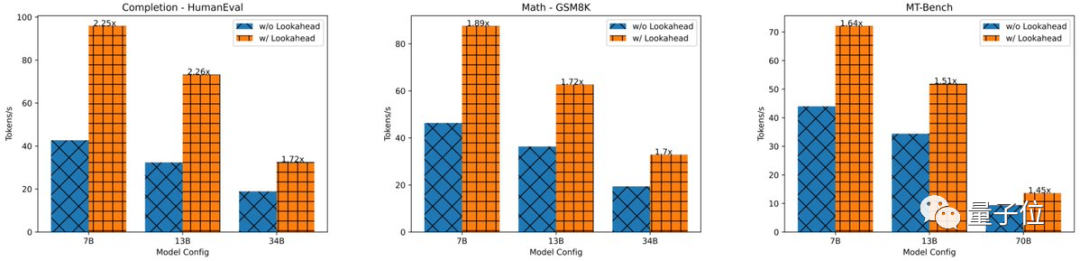
更重要的是，它允許分配更多（大于1個GPU）的 FLOP，以在對延遲極其敏感的應用程序中實現更大程度地延遲下降，盡管這會帶來收益遞減。

下面是具體介紹：

1、前向解碼的動機Jacobi在進行求解非線性系統(tǒng)時，一并使用定點迭代方法一次性解碼所有的未來token。

這個過程幾乎看不到時鐘加速。

2、前向解碼通過收集和緩存Jacobi迭代軌跡生成的n-grams來利用Jacobi解碼的能力。

下圖為通過Jacobi解碼收集2-grams，然后驗證并加速解碼的過程。

3、每個解碼步驟有2個分支：

前向分支維護一個固定大小的2D窗口，以根據Jacobi軌跡生成n-grams；驗證分支驗證有希望的n-grams。

作者實現了二合一atten mask，以進一步利用GPU的并行計算能力。

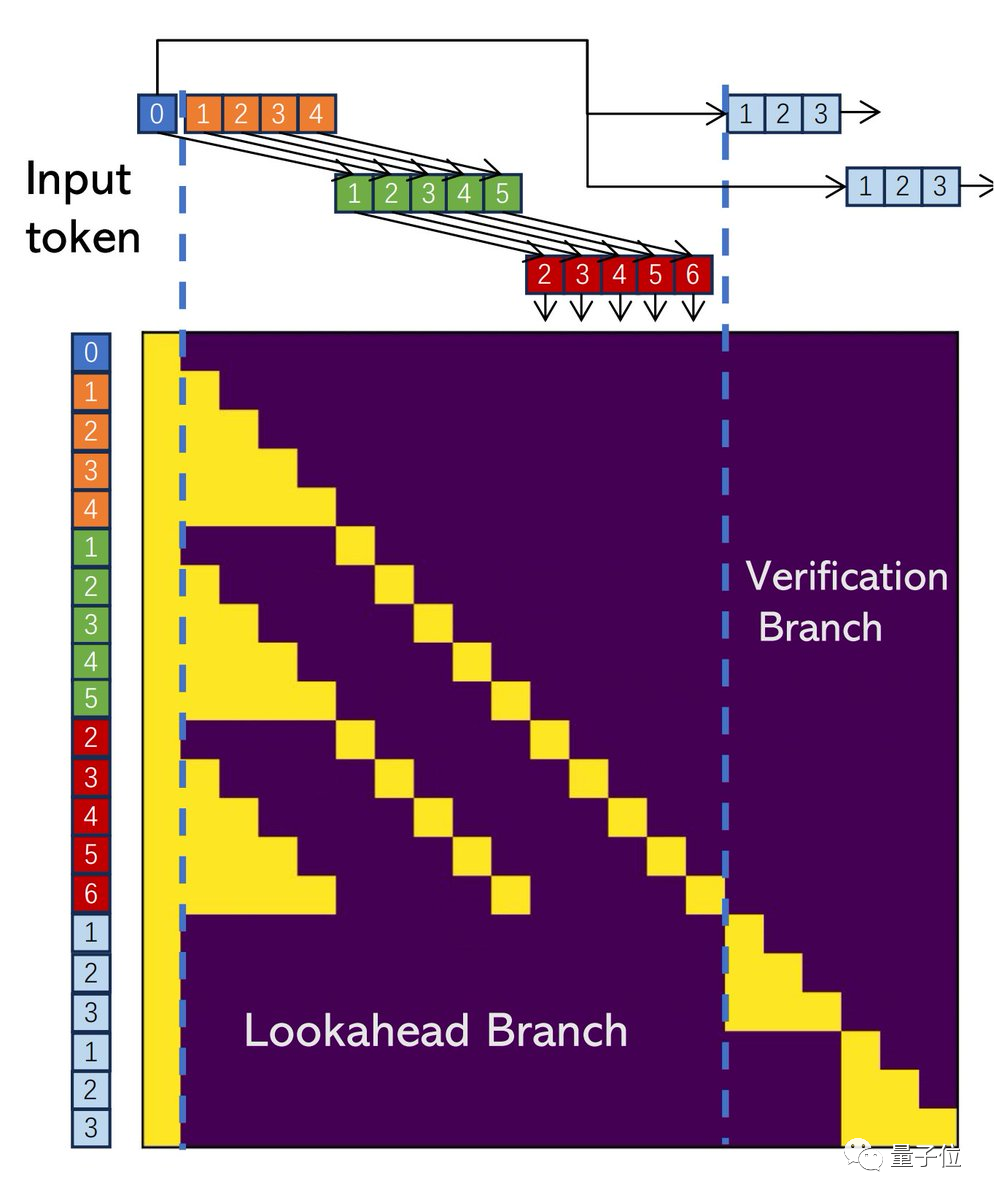
4、前向解碼無需外部源即可立即生成并驗證非常多的n-grams。這雖然增加了步驟的成本，但也提高了接受更長n-grams可能性。

換句話說，前向解碼允許用更多的觸發(fā)器來減少延遲。

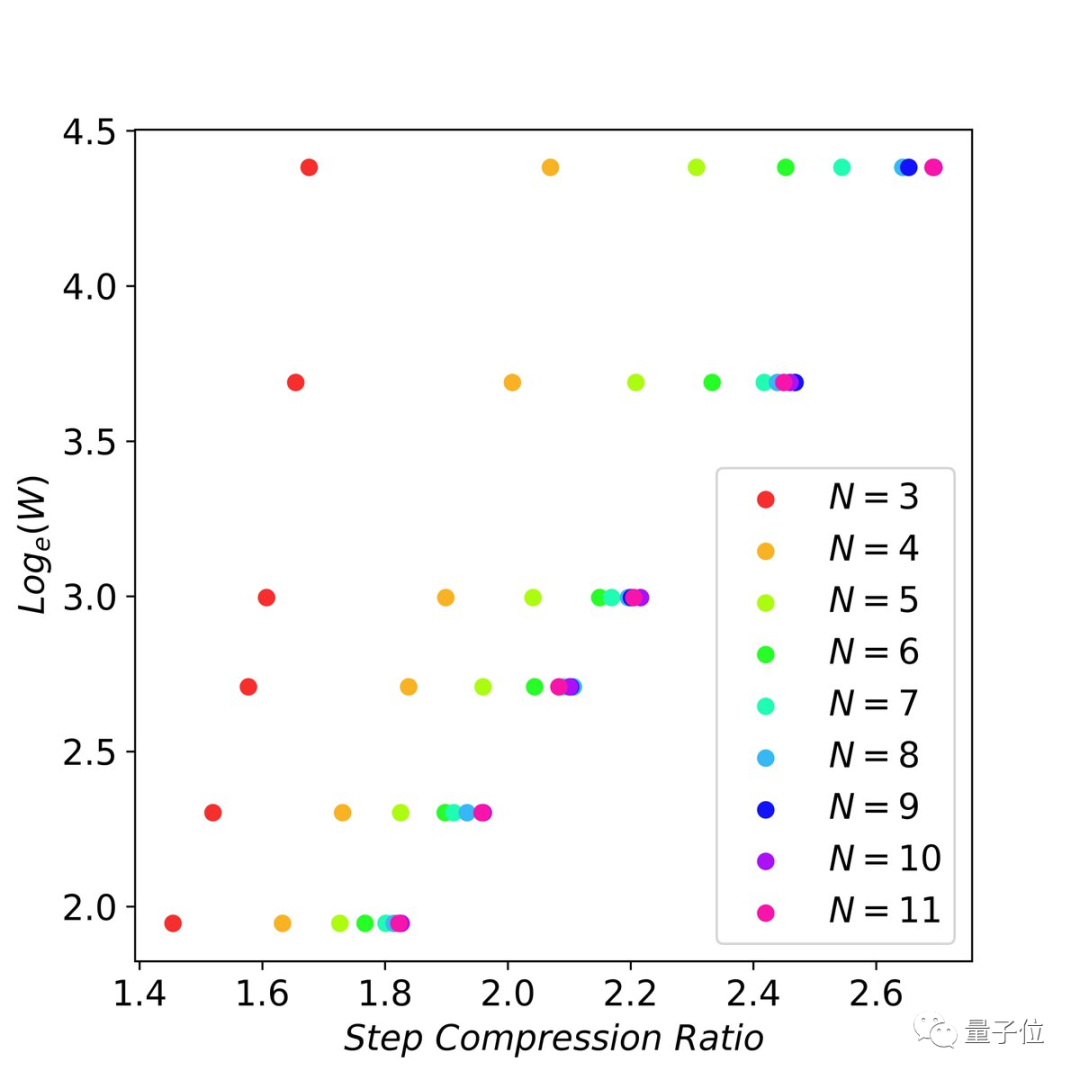
5、作者檢查了flops vs 延遲減少之間的縮放行為，并找到了縮放法則：
當n-grams足夠大時（比如11-gram），以指數方式增加未來的token猜測（即窗口大小）可以線性減少解碼步驟數。

作者介紹

本方法作者一共4位，全部來自小羊駝團隊。

其中有兩位華人：

傅奕超以及張昊，后者博士畢業(yè)于CMU，碩士畢業(yè)于上交大，現在是加州大學圣地亞哥分校助理教授。