本文經(jīng)自動駕駛之心公眾號授權(quán)轉(zhuǎn)載，轉(zhuǎn)載請聯(lián)系出處。

0.簡介

本文介紹了BEVTrack：鳥瞰圖中點(diǎn)云跟蹤的簡單基線。由于點(diǎn)云的外觀變化、外部干擾和高度稀疏性，點(diǎn)云的3D單目標(biāo)跟蹤（SOT）仍然是一個(gè)具有挑戰(zhàn)性的問題。值得注意的是，在自動駕駛場景中，目標(biāo)物體通常在連續(xù)幀間保持空間鄰接，多數(shù)情況下是水平運(yùn)動。這種空間連續(xù)性為目標(biāo)定位提供了有價(jià)值的先驗(yàn)知識。然而，現(xiàn)有的跟蹤器通常使用逐點(diǎn)表示，難以有效利用這些知識，這是因?yàn)檫@種表示的格式不規(guī)則。因此，它們需要精心設(shè)計(jì)并且解決多個(gè)子任務(wù)以建立空間對應(yīng)關(guān)系。本文《BEVTrack: A Simple Baseline for 3D Single Object Tracking in Bird’s-Eye View》（https://arxiv.org/pdf/2309.02185.pdf）中的BEVTrack是一種簡單而強(qiáng)大的三維單目標(biāo)跟蹤基線框架。在將連續(xù)點(diǎn)云轉(zhuǎn)換為常見的鳥瞰圖表示后，BEVTrack固有地對空間近似進(jìn)行編碼，并且通過簡單的逐元素操作和卷積層來熟練捕獲運(yùn)動線索進(jìn)行跟蹤。此外，為了更好地處理具有不同大小和運(yùn)動模式的目標(biāo)，BEVTrack直接學(xué)習(xí)潛在的運(yùn)動分布，而不像先前的工作那樣做出固定的拉普拉斯或者高斯假設(shè)。BEVTrack在KITTI和NuScenes數(shù)據(jù)集上實(shí)現(xiàn)了最先進(jìn)的性能，同時(shí)維持了122FPS的高推理速度。目前這個(gè)項(xiàng)目已經(jīng)在Github（https://github.com/xmm-prio/BEVTrack）上開源了。

1.主要貢獻(xiàn)

本文的貢獻(xiàn)總結(jié)如下：

1）本文提出了BEVTrack，這是一種簡單而強(qiáng)大的三維單目標(biāo)跟蹤的基線框架。這種開創(chuàng)性的方法通過BEV表示有效地利用了空間信息，從而簡化了跟蹤流程設(shè)計(jì)；

2）本文提出了一種新型的分布感知回歸策略，其直接學(xué)習(xí)具有不同大小和各種運(yùn)動模式的目標(biāo)的潛在運(yùn)動分布。該策略為跟蹤提供準(zhǔn)確的指導(dǎo)，從而提供了性能，同時(shí)避免了額外的計(jì)算開銷；

3）BEVTrack在保持高推理速度的同時(shí)，在兩個(gè)主流的基準(zhǔn)上實(shí)現(xiàn)了最先進(jìn)的性能

2.概述

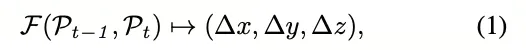
其中F是跟蹤器學(xué)習(xí)到的映射函數(shù)。

根據(jù)公式（1），我們提出了BEVTrack，這是一個(gè)簡單但強(qiáng)大的3D單目標(biāo)跟蹤基準(zhǔn)框架。BEVTrack的整體架構(gòu)如圖2所示。它首先利用共享的VoxelNext [29]提取3D特征，然后將其壓縮以獲得BEV表示。隨后，BEVTrack通過串聯(lián)和多個(gè)卷積層融合BEV特征，并通過MLP回歸目標(biāo)的平移。為了實(shí)現(xiàn)準(zhǔn)確的回歸，我們采用了一種新穎的分布感知回歸策略來優(yōu)化BEVTrack的訓(xùn)練過程。

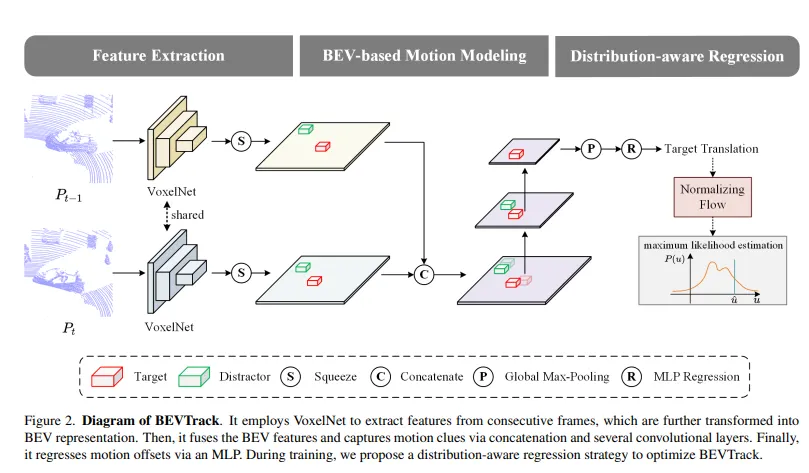
圖2. BEVTrack的示意圖。它使用VoxelNet從連續(xù)幀中提取特征，進(jìn)一步將其轉(zhuǎn)換為BEV表示。然后，通過串聯(lián)和幾個(gè)卷積層，它融合BEV特征并捕捉運(yùn)動線索。最后，通過多層感知機(jī)（MLP）回歸運(yùn)動偏移量。在訓(xùn)練過程中，我們提出了一種分布感知回歸策略來優(yōu)化BEVTrack。

3.特征提取

4.基于BEV的運(yùn)動建模

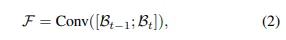
其中Conv表示BMM中的卷積塊，[;][;]表示連接運(yùn)算符。

其中H^′、W^′和C^′分別表示空間維度和特征通道數(shù)。

最后，我們使用最大池化層和多層感知器（MLP）來預(yù)測目標(biāo)平移偏移，即，

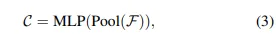
其中C ∈ \mathbb{R}^6表示目標(biāo)平移偏移\bar{u} ∈ \mathbb{R}^3的期望值和標(biāo)準(zhǔn)差σ ∈ \mathbb{R}^3，這將在第5節(jié)中詳細(xì)介紹。通過將平移應(yīng)用于目標(biāo)的最后狀態(tài)，我們可以在當(dāng)前幀中定位目標(biāo)。

5.分布感知回歸

在先前的工作中，通常在訓(xùn)練過程中使用傳統(tǒng)的L1或L2損失來進(jìn)行目標(biāo)位置回歸，這實(shí)際上對目標(biāo)位置的分布做出了固定的拉普拉斯或高斯假設(shè)。與之相反，我們提出直接學(xué)習(xí)底層運(yùn)動分布，并引入一種新穎的分布感知回歸策略。通過這種方式，可以為跟蹤提供更準(zhǔn)確的指導(dǎo)，使BEVTrack能夠更好地處理具有不同大小和移動模式的物體。

在[11]的基礎(chǔ)上，我們使用重新參數(shù)化來建模目標(biāo)平移偏移u～P(u)的分布。具體而言，P(u)可以通過對來自零均值分布z～P_Z(z)進(jìn)行縮放和平移得到，其中u=\bar{u}+σ·z，其中\(zhòng)bar{u}表示目標(biāo)平移偏移的期望，σ表示分布的尺度。P_Z(z)可以通過歸一化流模型（例如，real NVP [2]）進(jìn)行建模。給定這個(gè)變換函數(shù)，可以計(jì)算出P(u)的密度函數(shù)：

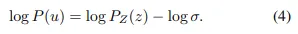
與之前僅回歸確定性目標(biāo)翻譯偏移量u的方法相比，我們的方法專注于回歸兩個(gè)不同的參數(shù)：目標(biāo)翻譯偏移量u的期望值\bar{u}和其標(biāo)準(zhǔn)差σ。

在這項(xiàng)工作中，我們采用了[11]中的殘差對數(shù)似然估計(jì)（RLE）來估計(jì)上述參數(shù)。RLE將分布P_Z(z)分解為一個(gè)先驗(yàn)分布Q_Z(z)（例如，拉普拉斯分布或高斯分布）和一個(gè)學(xué)習(xí)到的分布G_Z(z | θ)。為了最大化方程（4）中的似然函數(shù)，我們可以最小化以下?lián)p失函數(shù)：