昨天在群里面看到耳濡目染同志發(fā)了這么一張圖。

圖片

問的是 -1155459666 怎么變成 3139507630，這個(gè)問題比較有意思，雖然簡單，但涉及到了原碼、反碼、補(bǔ)碼相關(guān)的知識，本篇文章就來詳細(xì)解釋一下。

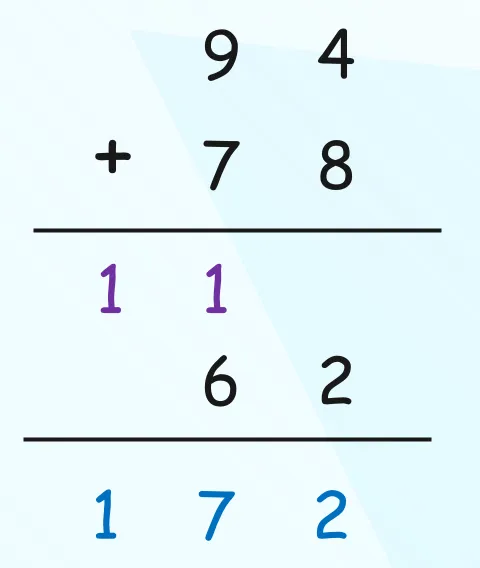
拋出一個(gè)問題，有兩個(gè)整數(shù) 94、78，如果讓你計(jì)算它們的和，你會怎么做？不用想，我們都會像下面這樣。

圖片

十進(jìn)制是逢十進(jìn)一，當(dāng)產(chǎn)生溢出時(shí)會往前進(jìn)一位，因此結(jié)果就是 110 + 062 等于 172。但計(jì)算機(jī)在運(yùn)算時(shí)會使用二進(jìn)制，本質(zhì)是一樣的，只不過二進(jìn)制是逢二進(jìn)一。

圖片

我們驗(yàn)證一下。

print(94 + 78)  # 172
print(0b10101100)  # 172

另外我們知道，與運(yùn)算時(shí)，如果兩個(gè)二進(jìn)制位均是 1，那么結(jié)果是 1，否則結(jié)果是 0；異或運(yùn)算時(shí)，如果兩個(gè)二進(jìn)制位相同，結(jié)果是 0，否則結(jié)果是 1。

# 與運(yùn)算，兩個(gè)二進(jìn)制位均是 1，結(jié)果才是 1
print(1 & 1)  # 1
print(1 & 0)  # 0
print(0 & 1)  # 0
print(0 & 0)  # 0

# 異或運(yùn)算，兩個(gè)二進(jìn)制位相同，結(jié)果為 0，相異結(jié)果為 1
print(1 ^ 1)  # 0
print(1 ^ 0)  # 1
print(0 ^ 1)  # 1
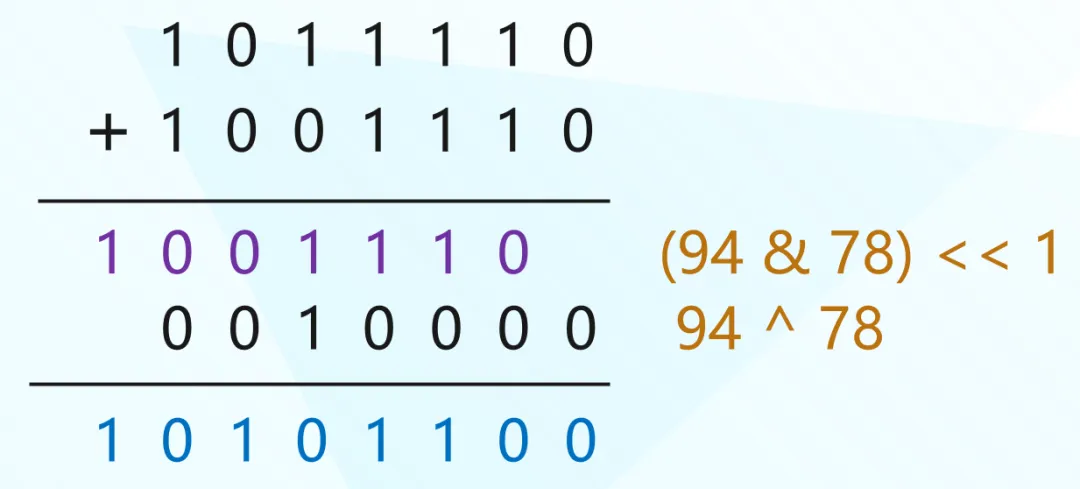
print(0 ^ 0)  # 0

然后再觀察一下之前的式子。

圖片

所以當(dāng)兩個(gè)整數(shù)相加時(shí)，我們還可以這么做。

a = 94
b = 78
# 無進(jìn)位加法
print(a ^ b)  # 16
# a + b 的進(jìn)位
# 既然是進(jìn)位，那么 (a & b) 要左移一位
print((a & b) << 1)  # 156
# 兩者相加
print(
    ((a & b) << 1) + (a ^ b)
)  # 172

當(dāng)然兩個(gè)整數(shù)直接相加的話，這么做沒啥意義，它一般會應(yīng)用于二分查找。在二分查找中，為了避免兩個(gè)整數(shù)相加溢出，求平均值的時(shí)候一般會這么做。

l = 123
r = 789
# 對于 C、Java 等語言來說，當(dāng) l、r 非常大時(shí)，相加可能會產(chǎn)生溢出
print((l + r) // 2)  # 456
# 因此一般都會這么做
print(l + (r - l) // 2)  # 456
# 但顯然還有更高效的做法
print((l & r) + ((l ^ r) >> 1))  # 456

然后來說一說原碼、反碼和補(bǔ)碼，不過首先我們要知道負(fù)數(shù)是如何表示的，對于一個(gè)有符號整數(shù)來說，它的最高位表示符號位。比如一個(gè) 8 位整數(shù)：

圖片

開頭的符號位如果為 0，則表示正數(shù)，為 1 則表示負(fù)數(shù)，然后剩余的有效位則表示具體的數(shù)值。比如 15 的二進(jìn)制是 1111，那么：

• 八位整數(shù) 15 的二進(jìn)制就是 00001111；
• 八位整數(shù) -15 的二進(jìn)制就是 10001111；
  

由于 7 個(gè)位能表示的最大整數(shù)是 2 的 7 次方減 1，所以八位整數(shù)的最大值就是 127，而最小值是 -128。那么問題來了，為什么最小值是 -128 呢？這就涉及到原碼、反碼和補(bǔ)碼了。

計(jì)算機(jī)為了人類閱讀方便，會以原碼的形式展示，但在計(jì)算和存儲的時(shí)候則是以補(bǔ)碼的形式。

• 對于正數(shù)來說，它的原碼、反碼、補(bǔ)碼是相同的。
• 對于負(fù)數(shù)來說，它的反碼等于原碼的符號位不變、其它位取反（1 變 0，0 變 1），而補(bǔ)碼則等于反碼加 1。當(dāng)然這是基于原碼求補(bǔ)碼，反過來也是一樣。反碼也等于補(bǔ)碼的符號位不變、其它位取反，然后再加 1 得到原碼，過程是一樣的。
  

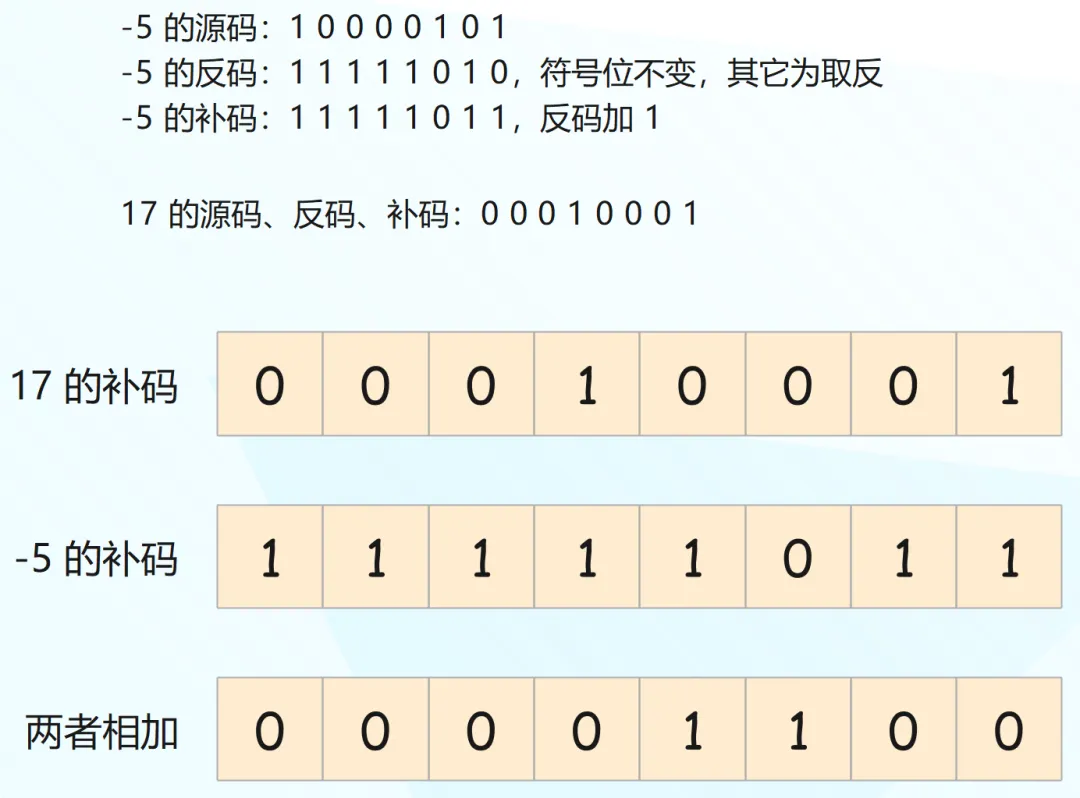
我們舉個(gè)例子，假設(shè)兩個(gè)八位整數(shù) 17 和 -5 相加。

圖片

因此 00001100 就是兩個(gè)整數(shù)的補(bǔ)碼相加之后的結(jié)果，也就是 12，由于是正數(shù)，它的原碼和反碼也是 12。

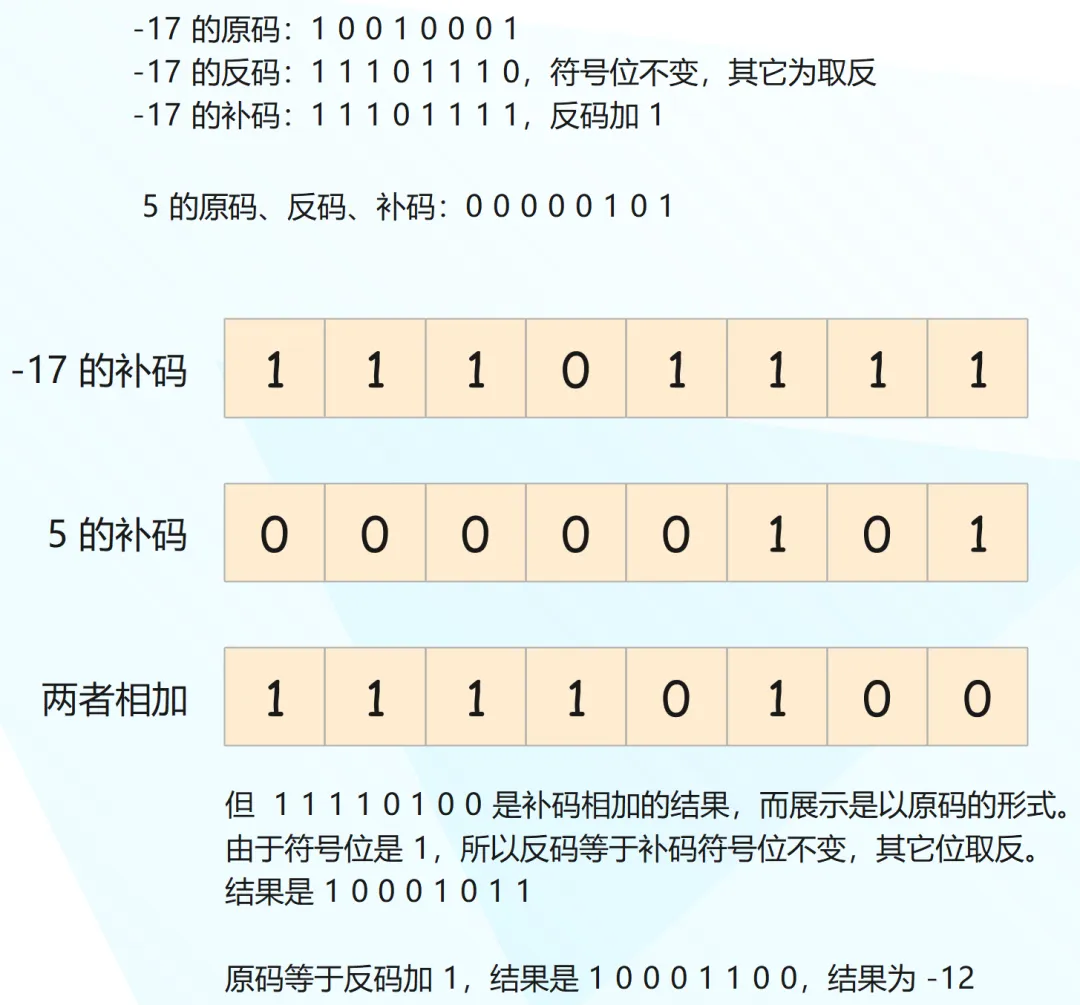
再舉個(gè)例子，假設(shè)兩個(gè)八位整數(shù) -17 和 5 相加。

圖片

相信你應(yīng)該明白整個(gè)邏輯了，計(jì)算機(jī)在存儲整數(shù)時(shí)會以補(bǔ)碼存儲，運(yùn)算也是以補(bǔ)碼的形式，但展示則是以原碼的形式。我們以 C 語言為例，來直觀感受一下這個(gè)過程。

#include <stdio.h>

int main(int argc, char const *argv[]) {   
    // 對于有符號整數(shù)來說，最高位表示符號位
    // 但對于無符號整數(shù)來說，所有的位都是有效位
    // 所以無符號八位整數(shù)的范圍是 0 ~ 255
    // 147 的二進(jìn)制為 0b10010011
    unsigned char num = 147;
    // 由于是正數(shù)，所以原碼、反碼、補(bǔ)碼都是 0b10010011
    printf("%hhu\n", num);  // 147
    // 但 C 語言不看你怎么存，就看你怎么讀
    // 如果以 %hhd 來讀取的話，那么會以有符號的格式打印八位整數(shù)
    // 此時(shí) 10010011 開頭的 1 就變成了符號位
    // 而計(jì)算機(jī)存儲的 10010011 是補(bǔ)碼，展示的時(shí)候要轉(zhuǎn)成原碼
    // 反碼：補(bǔ)碼符號位不變，其它位取反，等于 11101100
    // 原碼：反碼加 1，等于 11101101，轉(zhuǎn)成十進(jìn)制打印就是 -109
    printf("%hhd\n", num);  // -109
    return 0;
}

我們再舉個(gè)例子：

#include <stdio.h>

int main(int argc, char const *argv[]) {   
    // 八位有符號整數(shù) -1 的原碼是 1000_0001
    // 反碼是 1111_1110，補(bǔ)碼是 1111_1111
    // 所以計(jì)算機(jī)在存儲 -1 的時(shí)候，存的就是二進(jìn)制的 11111111
    char num = -1;
    // 但我們以無符號形式打印，那么 11111111 就全部都是有效位
    printf("%hhu\n", num);  // 255
    printf("%hhu\n", 0b11111111);  // 255

    // 再比如我們使用 16 位整數(shù)，原碼是 10000000_00000001
    // 那么補(bǔ)碼就是 11111111_11111111
    // 如果以無符號格式打印，結(jié)果顯然是 65535
    short num2 = -1;
    printf("%hu\n", num2);  // 65535
    printf("%hu\n", 0b1111111111111111);  // 65535

    // 32 位整數(shù)也是如此
    int num3 = -1;
    // 2 的 32 次方減 1，結(jié)果是 4294967295
    printf("%u\n", num3);  // 4294967295
    return 0;
}

總結(jié)，對于一個(gè)有符號整數(shù)來說：

• 如果是正數(shù)（符號位是 0），它的原碼、反碼、補(bǔ)碼是一致的。
• 如果是負(fù)數(shù)（符號位是 1），反碼等于原碼的符號位不變、其它位取反，補(bǔ)碼等于反碼加 1；或者反碼等于補(bǔ)碼的符號位不變、其它位取反，原碼等于反碼加 1。
  
  

計(jì)算機(jī)存儲和運(yùn)算使用的都是補(bǔ)碼，但展示的是原碼。

現(xiàn)在回到開頭的問題了，-1155459666 是怎么變成 3139507630 的。

圖片

還是那句話，不看你怎么存，就看你怎么讀，反正存儲的就是這一坨二進(jìn)制。如果以有符號格式讀取，最高位是符號位，結(jié)果就是 -1155459666；以無符號格式讀取，最高位也是有效位，結(jié)果就是 3139507630。

from ctypes import c_int, c_uint

print(c_int(-1155459666).value)
"""
-1155459666
"""
print(c_uint(-1155459666).value)
"""
3139507630
"""
print(0b10111011_00100001_00010101_10101110)
"""
3139507630
"""

那么問題來了，為什么要整出補(bǔ)碼這個(gè)東西出來呢？很好理解，有了補(bǔ)碼，加法和減法可以共用一套邏輯，無論是 a + b 還是 a - b，底層的運(yùn)算邏輯是相同的。

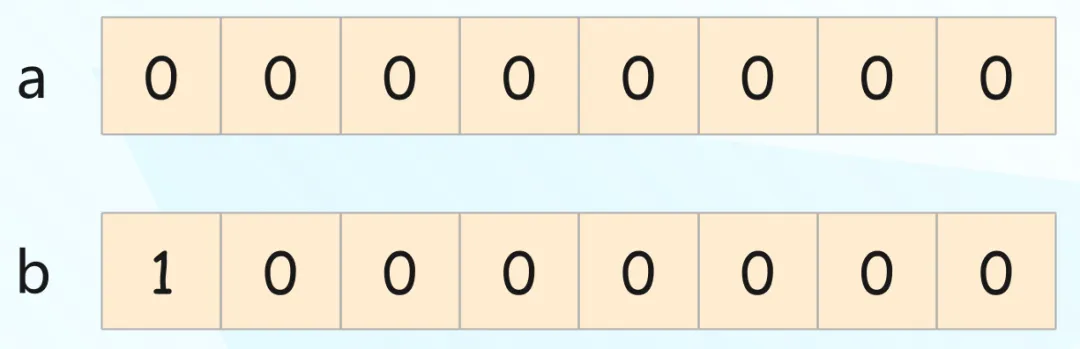
最后再來解釋一下，為什么有符號八位整數(shù)的最大值是 127，最小值是 -128。

圖片

兩個(gè)整數(shù) a 和 b，首先 a 的值肯定是 0，但問題是 b 的值是多少？難道是 -0 嗎？如果不考慮 0，那么有符號八位整數(shù)能表達(dá)的正數(shù)范圍是 1 ~ 127，負(fù)數(shù)范圍是 -1 ~ -127，然后還剩下兩個(gè) 0。于是讓 00000000 表示 0，讓 10000000 表示 -128。

圖片

不管是多少位的有符號整數(shù)，它的最小值的絕對值一定比最大值多 1，因此八位整數(shù)的最小值是 -128，最大值是 127。

事實(shí)上 10000000 表示 -128 有些人為規(guī)定的意思，但它確保了數(shù)字范圍的對稱性，并允許有效地利用二進(jìn)制位來表達(dá)整數(shù)。

以上就是整數(shù)在底層的存儲方式，以及原碼、反碼、補(bǔ)碼之間的關(guān)系。