一直以來，解決格上的近似最短向量問題（Lattice Problems）以及帶錯(cuò)誤學(xué)習(xí)問題（LWE），都是計(jì)算機(jī)領(lǐng)域的經(jīng)典算法難題。

尤其是在科學(xué)界看來，它們遠(yuǎn)遠(yuǎn)超出了傳統(tǒng)計(jì)算機(jī)的能力范圍。

那么，量子計(jì)算機(jī)有望能破解Lattice Problems以及LWE嗎？

前段時(shí)間，來自清華大學(xué)交叉信息研究院陳一鐳助理教授，便針對(duì)這些問題提出了一種全新的「破解格密碼的量子算法」。

預(yù)印本論文一經(jīng)發(fā)表，便在整個(gè)計(jì)算機(jī)界引起了巨大的轟動(dòng)。

如著名密碼學(xué)家N. P. Smart，就在第一時(shí)間發(fā)了篇博客文章，詳細(xì)討論了論文所帶來的影響。

文章地址：https://nigelsmart.github.io/LWE.html

具體來說，陳教授提出的這種多項(xiàng)式時(shí)間量子算法，主要用于求解具有特定多項(xiàng)式模數(shù)-噪聲比的「帶錯(cuò)誤學(xué)習(xí)問題」（LWE）。

通過結(jié)合Regev所提出的從網(wǎng)格問題到LWE的還原，便可以獲得多項(xiàng)式時(shí)間量子算法，并可以在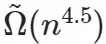的近似因子內(nèi)求解所有n維網(wǎng)格的決策最短向量問題（GapSVP）和最短獨(dú)立向量問題（SIVP）。

在此之前，還沒有已知的多項(xiàng)式甚至亞指數(shù)時(shí)間量子算法可以在任何多項(xiàng)式近似因子內(nèi)求解所有網(wǎng)格的GapSVP 或SIVP。

論文地址：https://eprint.iacr.org/2024/555.pdf

為了開發(fā)求解LWE的量子算法，作者提出了兩種新的技術(shù)：

首先，在量子算法的設(shè)計(jì)中引入具有復(fù)雜方差的高斯函數(shù)。特別是，利用復(fù)高斯函數(shù)離散傅里葉變換中的卡斯特波特征。

其次，使用帶有復(fù)高斯窗口的窗口量子傅里葉變換，從而能夠結(jié)合時(shí)域和頻域的信息。

基于此，便可以先將LWE實(shí)例轉(zhuǎn)換為具有純虛高斯振幅的量子態(tài)，然后將純虛高斯態(tài)轉(zhuǎn)換為L(zhǎng)WE秘密和誤差項(xiàng)的經(jīng)典線性方程，最后利用高斯消元法求解線性方程組。

但遺憾的是，Hongxun Wu（UC伯克利博二學(xué)生）和Thomas Vidick（量子領(lǐng)域?qū)＜遥┌l(fā)現(xiàn)，算法的第9步實(shí)際上存在一個(gè)尚不能修復(fù)的bug。

也就是說，這個(gè)通過多項(xiàng)式模數(shù)-噪聲比，來求解LWE的多項(xiàng)式時(shí)間量子算法，無法成立了。

對(duì)此作者表示，希望像復(fù)高斯（Complex Gaussian）和窗口QFT（windowed QFT）這樣的想法，會(huì)在量子計(jì)算中找到其他應(yīng)用，而LWE問題或許會(huì)將有別的解決方法。

九大關(guān)鍵步驟

首先進(jìn)行參數(shù)的設(shè)置，之后需要運(yùn)行一個(gè)由九個(gè)步驟組成的量子子程序，共運(yùn)行O(n)次。

論文中最關(guān)鍵的，是一個(gè)需要調(diào)用O(n)次的，由九個(gè)步驟組成的量子子程序。

其中，每次調(diào)用都會(huì)得到一個(gè)經(jīng)典線性方程，其隨機(jī)系數(shù)是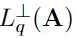中最短的向量（與LWE秘密向量和錯(cuò)誤向量相關(guān)）。

在調(diào)用完O(n)次之后，便可以得到一個(gè)全秩線性方程組，并通過高斯消元法計(jì)算出LWE秘密和錯(cuò)誤項(xiàng)。

步驟 1：在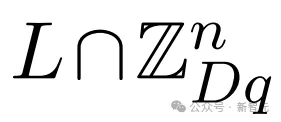上進(jìn)行疊加，并應(yīng)用復(fù)高斯窗口

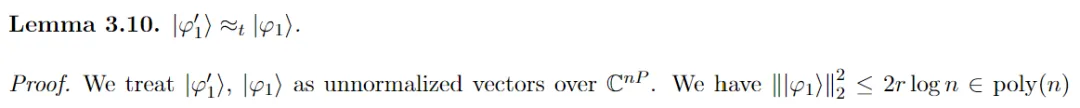
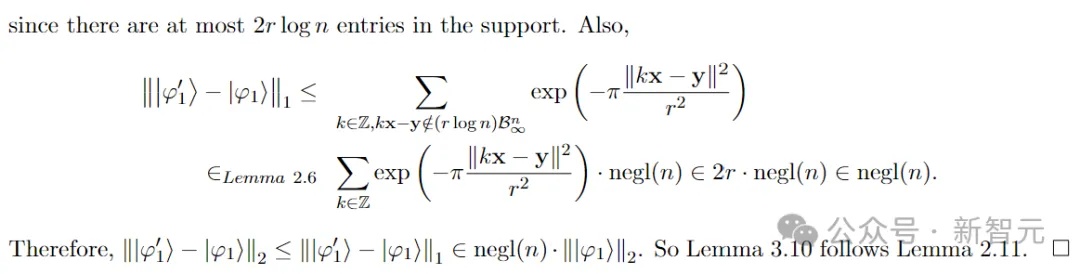
步驟 2：在|φ1?上應(yīng)用

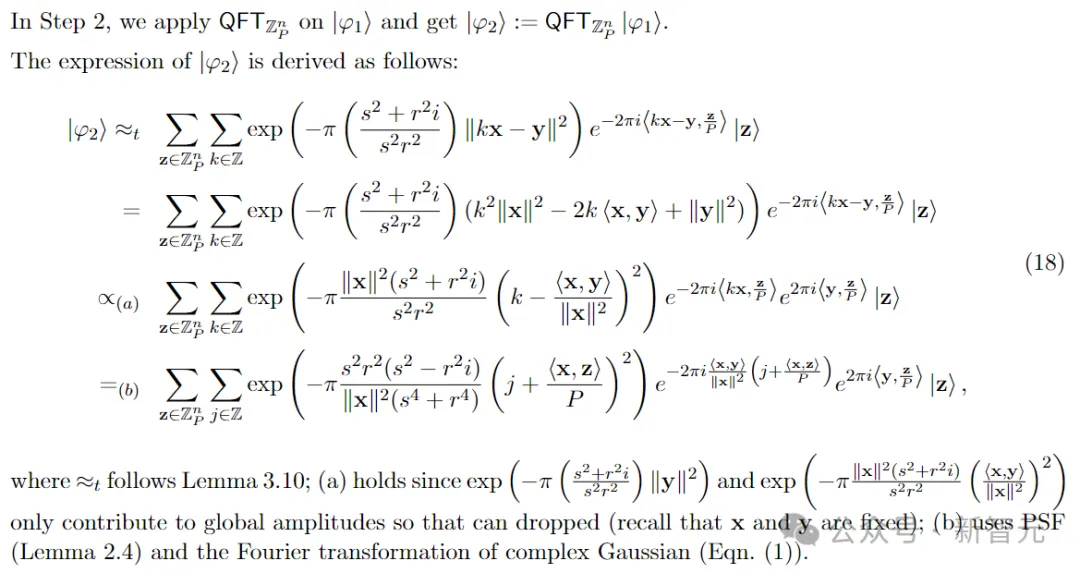
步驟 3：在|φ2?上應(yīng)用復(fù)高斯窗口，得到|φ3?和z′

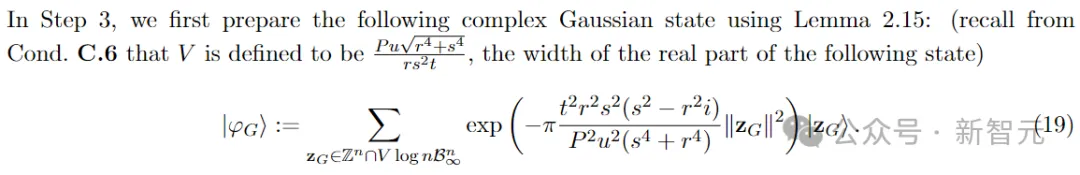
步驟 4：在|φ3?上應(yīng)用

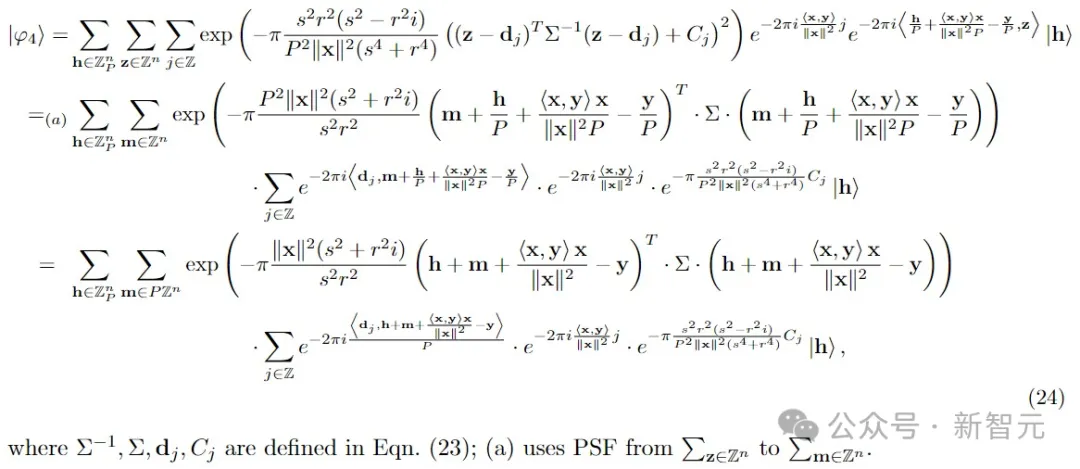
步驟 5：將|φ4?分割成高階|h′?和低階|h′′?，然后對(duì)|h′′?進(jìn)行測(cè)量

步驟 6：在|φ5?上應(yīng)用

步驟 7：提取|φ6?的中心，得到純虛高斯?fàn)顟B(tài)|φ7?

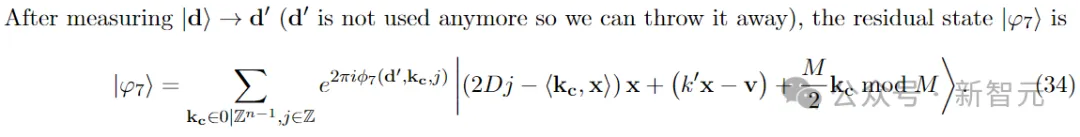
步驟 8：提取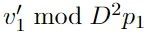并保留|φ8?=|φ7?

在步驟8中，作者首先進(jìn)行四次運(yùn)算（可逆），然后進(jìn)行部分測(cè)量，最后將四次運(yùn)算反轉(zhuǎn)。也就是說，需要在不折疊或修改|φ7?的情況下，學(xué)習(xí)。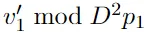

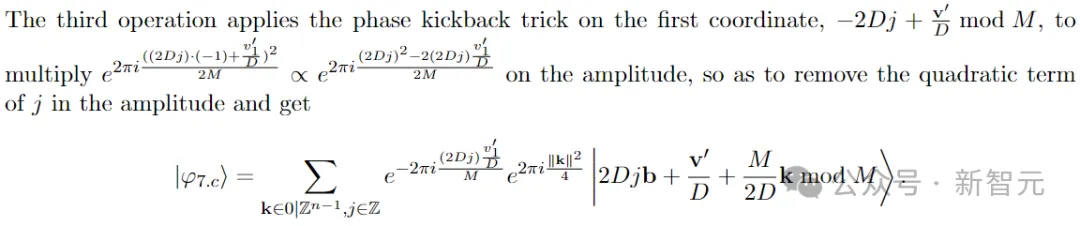
步驟 9：從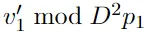和|φ8?中提取秘密的線性方程

第9步的目標(biāo)是將|φ8?轉(zhuǎn)換為秘密的經(jīng)典線性方程，并最終得到主Lemma（3.8）的證明。

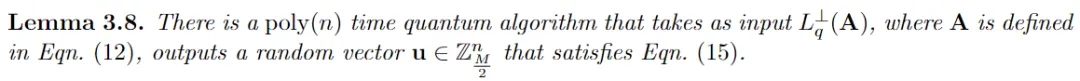
其中，步驟9使用步驟8中獲得的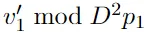信息，以及插入LWE秘密中的已知項(xiàng)的κ-1坐標(biāo)。

這里，bug來了：|φ8.f?的振幅不滿足M2周期性。

或者，另一種解釋是：|φ8.f?包含p1...pκ向量。經(jīng)過域擴(kuò)展后，本應(yīng)得到p1p2...pκ-p2...pκ向量，但按照|φ8.g?的寫法，它只包含p1...pκ向量。因此|φ8.g?的表達(dá)式是錯(cuò)誤的。

作者介紹

陳一鐳是清華大學(xué)交叉信息學(xué)院（IIIS）的一名助理教授。

此前，他在波士頓大學(xué)獲得博士學(xué)位，指導(dǎo)老師是Ran Canetti教授和Leonid Reyzin教授。并在上海交通大學(xué)獲得學(xué)士學(xué)位。在那里，一個(gè)有趣的問題引導(dǎo)他走上了科研之路。

他的研究興趣是密碼學(xué)，特別是在偽隨機(jī)，格密碼，數(shù)論，和量子計(jì)算等方向。

主要成果有：設(shè)計(jì)了格問題的量子算法，建立了多線性映射和代碼混淆在格問題上安全實(shí)現(xiàn)的基礎(chǔ)，提出了證明Fiat-Shamir假設(shè)的方法，以及提出了一個(gè)不可逆群的構(gòu)造。