在計算機領域，解決格上的近似最短向量問題（Approximate Shortest Vector Problems in Lattices。Lattice Problems）以及與之等價的容錯學習問題（Learning with Errors，LWE）是經典的算法難題，科學界普遍認為它們超出了傳統計算機的能力范圍。

量子計算機是否有望能破解 Lattice Problems 以及 LWE？雖然這一問題長期以來受到關注，但鮮有實質性進展。

近日，清華大學交叉信息研究院助理教授陳一鐳在 eprint 上發布的一篇論文，給出了破解格密碼的量子算法，引發了全球計算機領域的震撼。

• 論文地址：https://eprint.iacr.org/2024/555.pdf
• 論文標題：Quantum Algorithms for Lattice Problems

清華大學在今天的官方公告中表示：「陳一鐳的工作提出了一個全新的量子算法來解決 LWE 以及與之等價的格問題。這項工作仍在同行評議中。如果被驗證為正確，將為這個懸而未決的問題給出肯定的答復。」

它在科學上的意義將是雙層的：第一，這將是自 30 年前 Peter Shor 提出大數分解的量子算法以來，最重要的量子算法突破。

第二，這將對美國 NIST 過去 10 年來選擇后量子密碼設計的思路產生顛覆性的影響，因為多數選出的后量子密碼方案都是基于 Lattice Problems 或 LWE。陳一鐳的工作無疑將使他們安全性受到質疑。

這篇論文提出的算法及分析極為新穎而深奧。回想 Wiles 1994 年解決費馬大定理（Fermat's Last Theorem），以及 Perelman 2002 年解決龐佳萊猜想（Poincaré Conjecture）后，都經過一年以上專家們方能徹底認證其正確性。陳一鐳的工作，預料也需要數月時間才能完成驗證認可。我們靜候科學界對此工作的后續反應。

對此，圖靈獎得主、量子計算領域權威、清華交叉信息研究院院長姚期智給出高度評價：「作為一個青年教師，陳一鐳能勇于挑戰如格密碼這樣的世界級科學難題，令人贊佩！」

從論文致謝部分的內容來看，為理論計算機領域引入格密碼和容錯學習問題的紐約大學計算機科學家、2018 年哥德爾獎得主 Oded Regev 本人應該已經看過論文手稿。

那么，這篇論文究竟取得了怎樣的突破？

具體而言，這篇論文展示了一種多項式時間量子算法，用于求解具有特定多項式模數 - 噪聲比的有誤學習問題（LWE）。結合 Regev [J.ACM 2009] 所展示的從格問題到 LWE 的還原，論文得到了多項式時間量子算法，用于求解所有 n 維網格的決定性最短向量問題（GapSVP）和最短獨立向量問題（SIVP），其近似因子為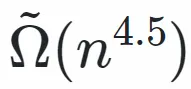。在此之前，還沒有任何多項式甚至亞指數時間的量子算法可以在任何多項式近似因子內求解所有格的 GapSVP 或 SIVP。

為了開發求解 LWE 的量子算法，這篇論文主要引入了兩種新技術：

首先，陳一鐳在量子算法的設計中引入了具有復雜方差的高斯函數，特別是利用了復高斯函數離散傅里葉變換中的卡斯特波特征。其次，陳一鐳使用帶有復高斯窗口的窗口量子傅里葉變換，這使得能夠結合時域和頻域的信息。利用這些技術，陳一鐳將 LWE 實例轉換為具有純虛高斯振幅的量子態，然后將純虛高斯態轉換為 LWE 秘密和誤差項的經典線性方程，最后利用高斯消元法求解線性方程組。

求解 LWE 的量子算法

論文第三章主要專注于定理的證明：

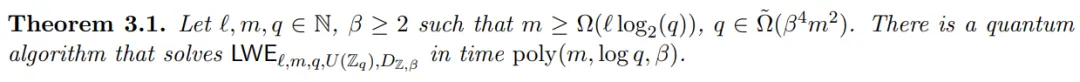
• 3.1 節展示了具有幾個已知秘密坐標的 LWE 和標準 LWE 一樣難；
• 3.2 介紹了將 LWE 轉換成具有唯一最短向量的特殊 q-ary 格；
• 3.3 節列出了主要量子算法中使用的參數；
• 3.4 節概述了主要的量子算法；
• 3.5 節詳細提供了主要量子算法的九個步驟，但將所有長度超過三頁的證明推遲到第 3.6 節；
• 3.6 節提供了第 3.5 節中遺漏的所有詳細證明。

具體而言：

論文展示了 LWE 的三種變體，最后一個變體在 Def. 3.4 中正式定義，本文提出的量子算法最終將解決這個問題。 

下面三種縮減都是對現有經典多項式時間縮減的微小修改，從標準 LWE 到它們的變體。

1. 有 k 個無誤差坐標的 LWE。

2. 有 k 個選擇誤差項的 LWE。

3.LWE，秘密遵循誤差分布。

將 LWE 轉換成具有唯一最短向量的特殊 q-ary 格

現在定義一個 q-ary 格，使得找到這個特殊 q-ary 格的唯一最短向量意味著求解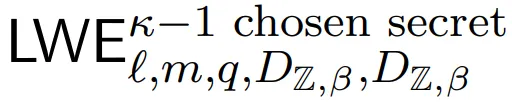。設：

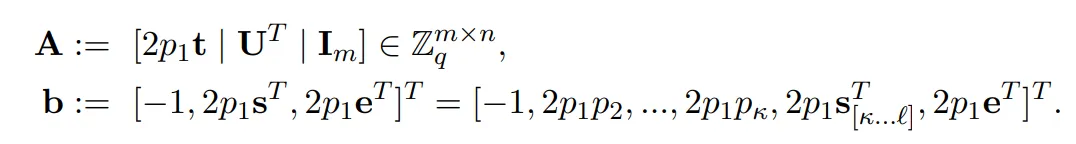
參數選擇

本小節將介紹更多量子算法中使用的參數。設 D ∈ N + 為縮放參數。

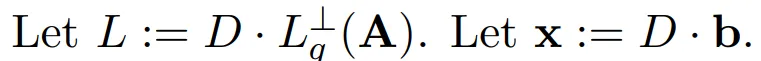
參數是在以下約束下設置的（ ）：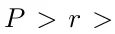

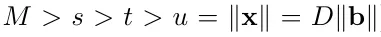量子算法有九個步驟，下面的每個條件通常只在一個或幾個步驟中使用：

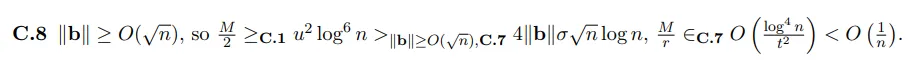
主要量子算法的詳細概述

本節中，作者運行一個由 9 大步驟組成的量子子程序，時間復雜度為 O (n) 次。每次運行量子子程序時都會獲得一個經典線性方程，其中隨機系數在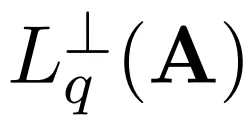中的最短向量上（與 LWE 秘密和誤差向量相關）。因此，運行 O (n) 次后將得到一個滿秩線性方程組，并通過高斯消元法計算 LWE 秘密項和誤差項。

如下為量子子程序中 9 大步驟的高級描述，包括了每個步驟中獲得的狀態以及經典信息。 

主要量子子程序：9 大步驟詳解

步驟 1：在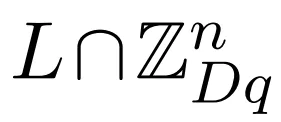上準備一個疊加，并應用復高斯窗。

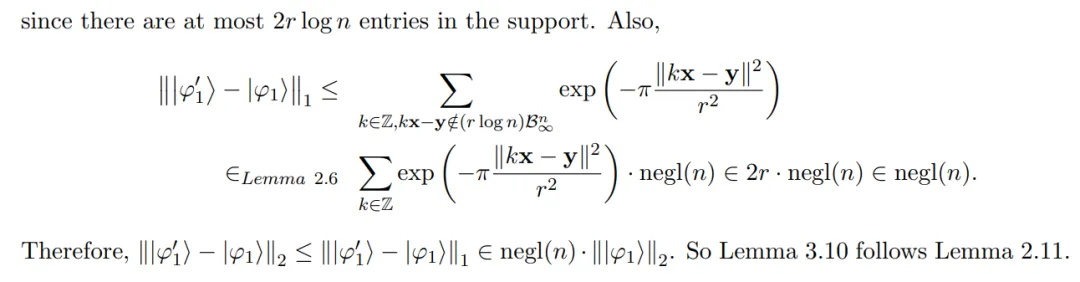
步驟 2：在 |φ1?上應用。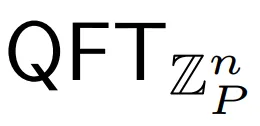

步驟 3：在 |φ_2?上 應用復高斯窗，得到 |φ_3? 和 z′。

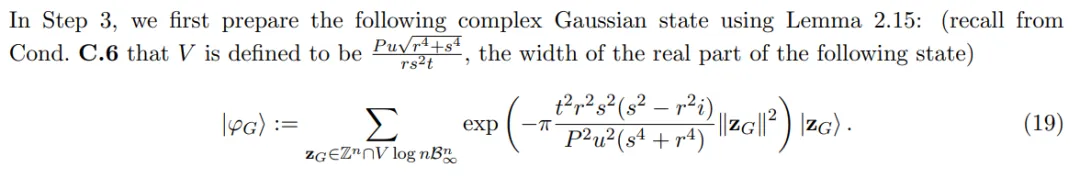
步驟 4：在 |φ_3?上應用。

步驟 5：將 |φ_4? 劃分為了高階和低階 |h′? |h′′?，然后測量 |h′′?。為了推導出 |φ_5?的表達式，作者注意到 |φ_4? 可以等效地寫為：

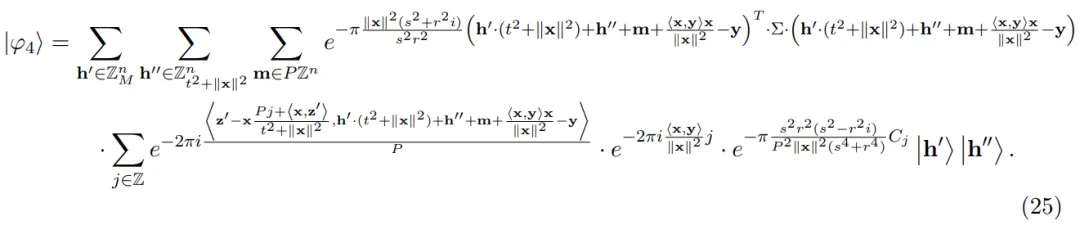
步驟 6：在 |φ_5?應用。

步驟 7：提取 |φ_6? 的中心，得到純虛高斯態 |φ_7?。

步驟 8：提取 v′_1 mod D^2_p1 并保留 |φ_8? = |φ_7?。

在第 8 步中，作者首先執行四次操作，然后進行部分測量，最后將這四次操作反轉（將確保這四次操作是可逆的）。目標是提取 v′_1 mod D^2_p1，最終返回到 |φ_7?。也就是說，將學習 v′_1 mod D^2_p1 而不折疊或修改 |φ_7?。

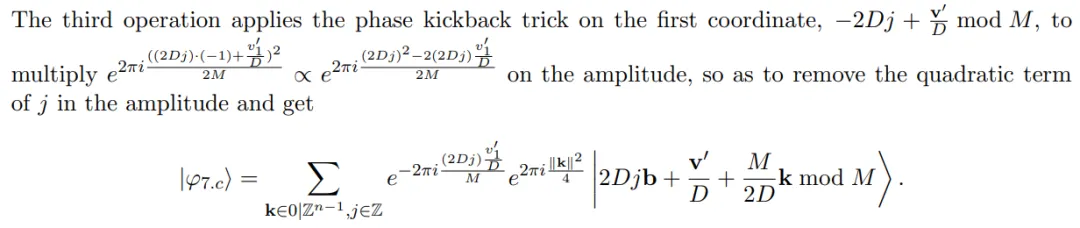
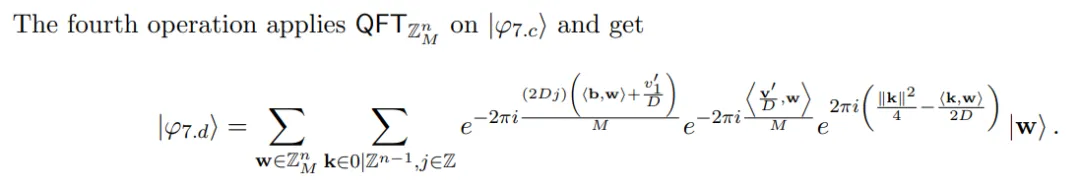
步驟 9：從 v′_1 mod D^2_p1 和 |φ_8? 中提取秘密上的線性方程。

在第 9 步中，作者的目標是將 |φ_8? 轉換為秘密上的經典線性方程，最終給出如下主引理（引理 3.8）的證明。步驟 9 使用步驟 8 中獲得的 v′_1 mod D^2_p1 信息，并插入 LWE 秘密中的已知項的 κ-1 坐標。

陳一鐳簡介

陳一鐳是清華大學交叉信息學院助理教授，上海期智研究院 PI。曾任 VISA 研究院研究員。于 2018 年獲得波士頓大學計算機博士學位，本科畢業于上海交通大學。主要研究興趣是密碼學，特別是在偽隨機，格密碼，數論，和量子計算等方向。

在個人介紹中，陳一鐳的研究成果主要包括設計了格問題的量子算法，建立了多線性映射和代碼混淆在格問題上安全實現的基礎，提出了證明 Fiat-Shamir 假設的方法，以及提出了一個不可逆群的構造。

也就是說，在 2022 年，陳一鐳就發表了有關格問題的研究。該研究「Quantum Algorithms for Variants of Average-Case Lattice Problems via Filtering」發表于 2022 年歐洲密碼大會（Eurocrypt 2022），并收到 Journal of Cryptology 邀稿。

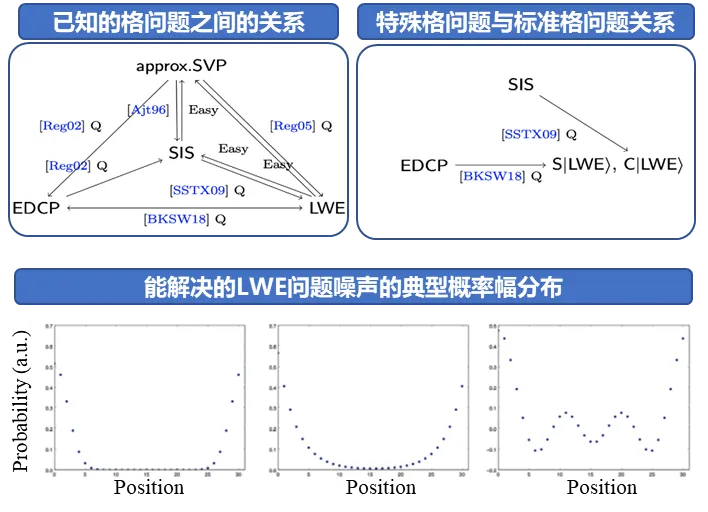
在 2022 年這篇研究中，陳一鐳團隊和普林斯頓大學的劉啟鵬和 Mark Zhandry 提出了一個能解決特殊格問題的多項式時間量子算法。這些特殊格問題是 SIS 和 LWE 的變種。他們雖然并不等價于標準的格問題，但是已經非常接近于密碼學常用的問題。他們的量子算法中使用了一種被稱為 “過濾” 的方法，是在量子算法的設計中第一次使用，可能為未來量子算法的設計帶來新的思路。