騰訊混元、北大發現Scaling law「浪涌現象」,解決學習率調參難題
過去十年間,基于隨機梯度下降(SGD)的深度學習模型在許多領域都取得了極大的成功。與此同時各式各樣的 SGD 替代品也如雨后春筍般涌現。在這些眾多替代品中,Adam 及其變種最受追捧。無論是 SGD,還是 Adam,亦或是其他優化器,最核心的超參數非 Learning rate 莫屬。因此如何調整好 Leanring rate 是煉丹師們從一開始就必學的技能。
從直覺上講,影響 Learning rate 取值的重要因素是 Batch size。不知你在學習煉丹術時,是否遇到或者思考過入如下問題:
- 我的 Batch size 增加一倍,Learning rate 該怎么調整?
- 網上有說 Batch size 和 Learning rate 是線性放縮,也有說是平方根放縮,到底該按照哪個調整?
- 為什么我按照網上說的經驗關系調整之后效果反而變差了?
針對上述問題,騰訊混元聯合北京大學基于現有科研基礎和實際業務需求,在進行了大量理論分析和實驗驗證后發布了關于 Batch size 和 Learning rate 放縮關系的調參指南:

- 論文:Surge Phenomenon in Optimal Learning Rate and Batch Size Scaling
- 論文地址:https://arxiv.org/pdf/2405.14578
1. 當使用 SGD 風格的優化器時,應當采用 OpenAI 2018 年給出的結論(https://arxiv.org/pdf/1812.06162):
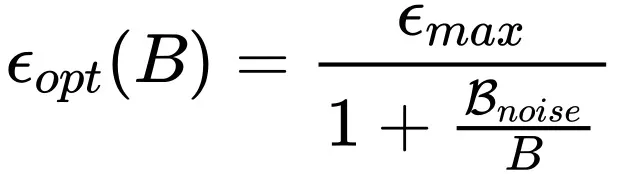
2. 但是當使用 Adam 風格的優化器時,需要按照如下放縮規律:

其中 和 B 分別代表 Learning rate 和 Batch size,而
和 B 分別代表 Learning rate 和 Batch size,而 與 OpenAI 2020 年 Scaling law 論文(https://arxiv.org/pdf/2001.08361)中的
與 OpenAI 2020 年 Scaling law 論文(https://arxiv.org/pdf/2001.08361)中的 對應。從上面結論不難發現,當
對應。從上面結論不難發現,當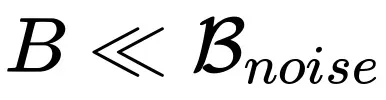 時,社區中廣為流傳的線性放縮和平方根放縮在一定范圍內都是正確的,并且分別對應使用 SGD 風格和 Adam 風格優化器的情況。
時,社區中廣為流傳的線性放縮和平方根放縮在一定范圍內都是正確的,并且分別對應使用 SGD 風格和 Adam 風格優化器的情況。
一、居然要降低學習率?
如果仔細觀察 Adam 風格優化器放縮規律的表達式子會發現,當 Batch size 超過 后,隨著 Batch size 增加最優的 Learning rate 反而是下降的!這樣的結論似乎有點反常,但是仔細思考之后又覺得是合理的。首先我們回顧一下 Adam 的更新形式,梯度的一階動量除以二階動量的平方根:
后,隨著 Batch size 增加最優的 Learning rate 反而是下降的!這樣的結論似乎有點反常,但是仔細思考之后又覺得是合理的。首先我們回顧一下 Adam 的更新形式,梯度的一階動量除以二階動量的平方根:
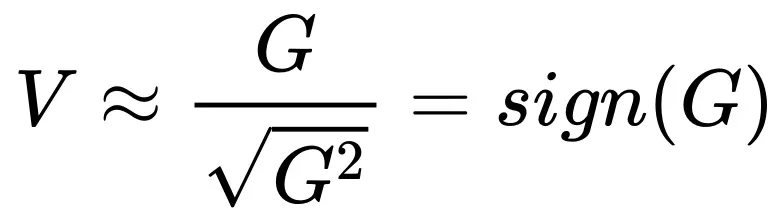
(更詳細的討論參考原文中的附錄 A)。與 SGD 直接采用 G 進行參數更新相比,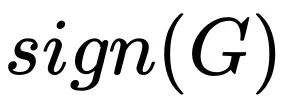 將更快的進入飽和區間,例如,假設 G 的均值是正實數,隨著 Batch size 增加
將更快的進入飽和區間,例如,假設 G 的均值是正實數,隨著 Batch size 增加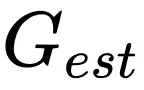 估計為正數時,再增加估計的準確度對
估計為正數時,再增加估計的準確度對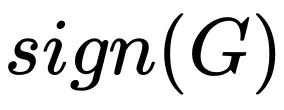 的結果也毫無影響了。因此當 Batch size 超過
的結果也毫無影響了。因此當 Batch size 超過 時,增加的信息不足以抵消
時,增加的信息不足以抵消 帶來的噪聲影響,從而導致此次的更新不再那么確信,以至于需要降低學習率。
帶來的噪聲影響,從而導致此次的更新不再那么確信,以至于需要降低學習率。
二、觀察到的下降區間
為了檢驗理論的正確性,需要從實驗中觀察到最優學習率的 “下降區間”。既然從上一節的分析中發現,使用 Adam 優化器時 Batch size 超過 就會導致最優學習率下降,那么只要確定出
就會導致最優學習率下降,那么只要確定出 取值,然后在通過網格搜索打點觀察就可以了。雖然從形式上
取值,然后在通過網格搜索打點觀察就可以了。雖然從形式上 計算很困難,但是幸運的是基于 OpenAI 關算于訓練時間和樣本效率的定量結論中我們可以估算出
計算很困難,但是幸運的是基于 OpenAI 關算于訓練時間和樣本效率的定量結論中我們可以估算出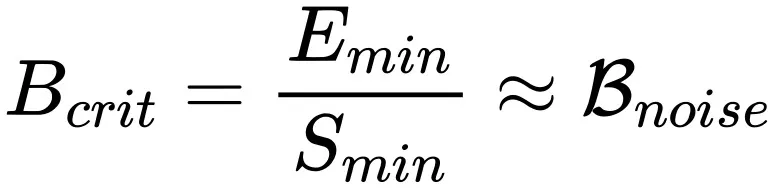 的取值(更詳細的討論參考原文中的附錄 G)。
的取值(更詳細的討論參考原文中的附錄 G)。
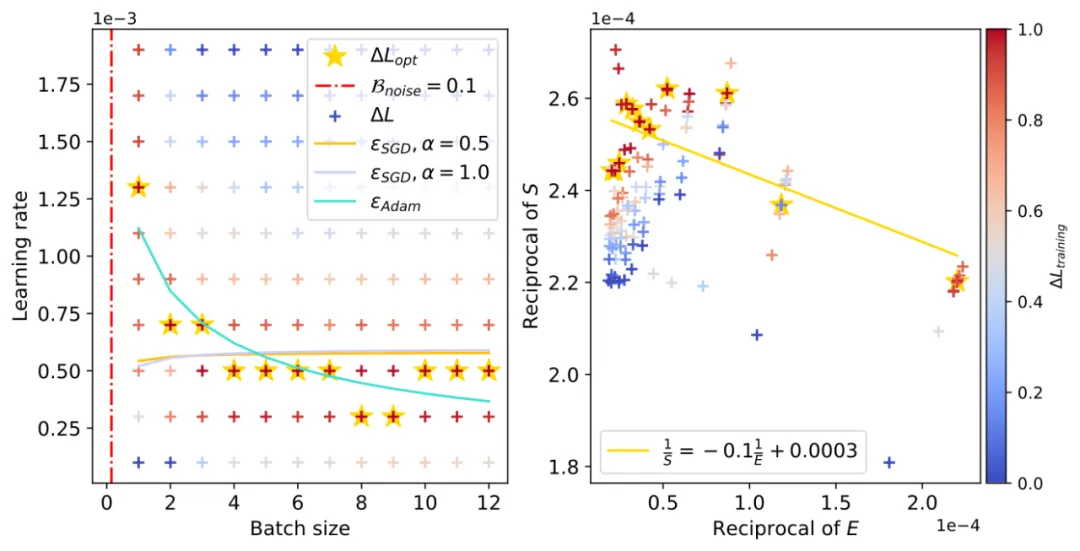
上面展示了 CNN 在 FashionMNIST 上的學習率 “下降區間”。左圖為通過 OpenAI 定量公式估算的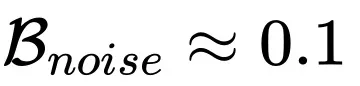 (左圖直線斜率的負數,右圖紅色豎直虛線),右圖中黃色五角星代表不同 Batch size 下的最優 Learning rate 取值,青色實線為我們的理論預估曲線。
(左圖直線斜率的負數,右圖紅色豎直虛線),右圖中黃色五角星代表不同 Batch size 下的最優 Learning rate 取值,青色實線為我們的理論預估曲線。

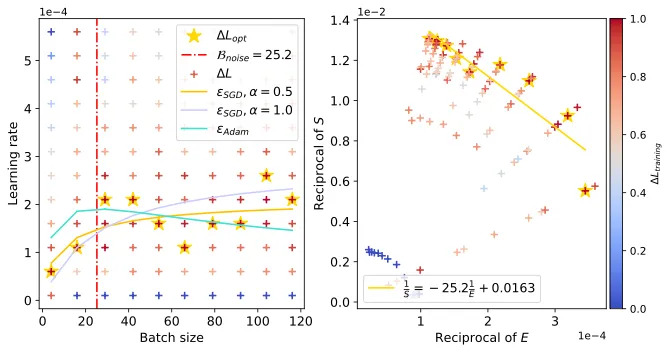
以及 Resnet18 在 TinyImagenet,和 DistilGPT2 在 Eli5Category 上也觀察到了類似現象。
三、浪涌現象
前面我們從理論和實驗上都發現了,在使用 Adam 風格優化器時最優學習率曲線就像一朵 “浪花” 一樣隨著 Batch size 增加會先升高后下降。同時結合 OpenAI scaling law 的結論,隨著訓練進行 會逐漸變大。我們理論預測并實驗證明了隨著訓練進行 “浪花” 逐漸向著大 Batch size 方向涌動:
會逐漸變大。我們理論預測并實驗證明了隨著訓練進行 “浪花” 逐漸向著大 Batch size 方向涌動:
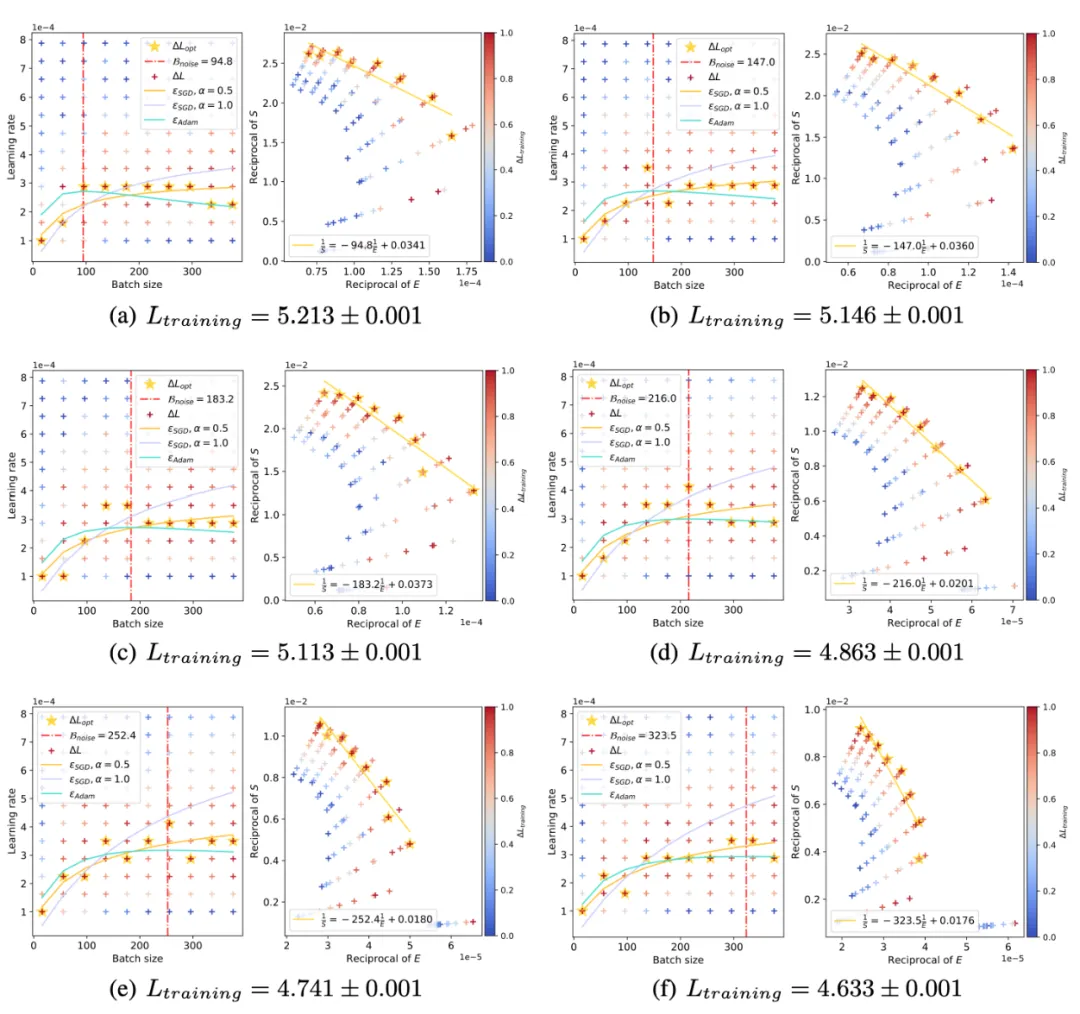
四、理論發現
前面討論過 Adam 風格的優化器在進行參數更新時采用類似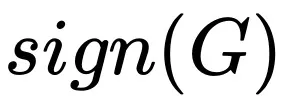 的形式。雖然此形式看起來很簡單,但是由于推導過程涉及到對更新量均值和方差的考量,所以我們在處理的時候做了一個假設和一個近似:
的形式。雖然此形式看起來很簡單,但是由于推導過程涉及到對更新量均值和方差的考量,所以我們在處理的時候做了一個假設和一個近似:
1. 假設每個樣本的參數 i 的梯度服從均值為 ,方差為
,方差為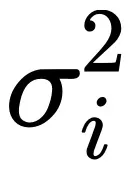 的高斯分布
的高斯分布
2. 通過 sigmoid-style 函數對高斯誤差函數進行數值近似
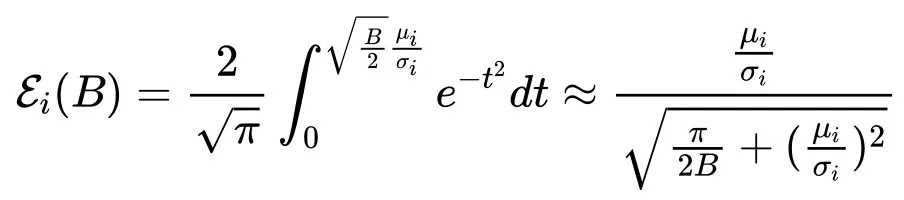
當 時,完整的 Scaling law 形式近似為:
時,完整的 Scaling law 形式近似為:
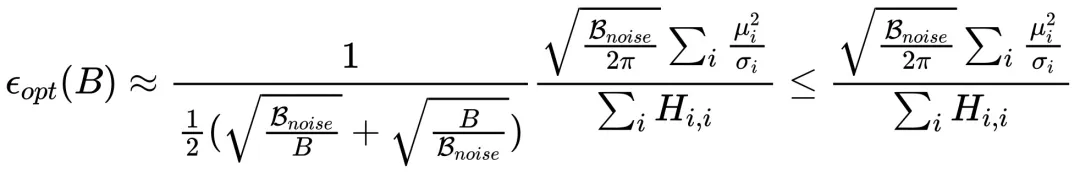
其中

,H 為海森矩陣。
當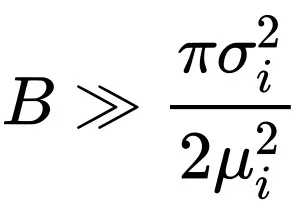 時:
時:
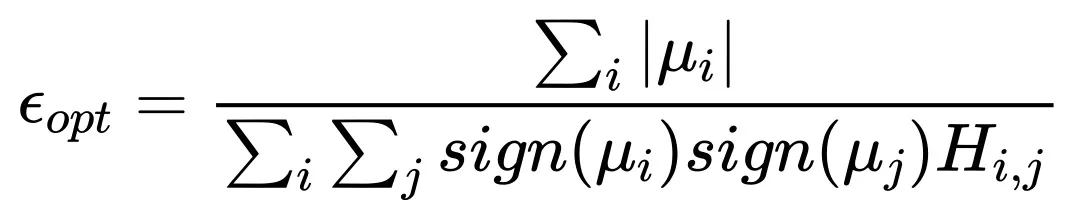
表明,Batch size 無限大時最優學習率趨于一個飽和值。
五、應用
我們在騰訊 Angel 大模型訓練框架中集成了上述理論成果,并在騰訊混元大模型訓練任務中對理論進行進一步驗證,未來將服務于各種大模型訓練場景。
感謝閱讀,更多詳細內容,請參考原文。