遺傳算法是一個優(yōu)化技術，在本質上類似于進化過程。這可能是一個粗略的類比，但如果你瞇著眼睛看，達爾文的自然選擇確實大致上類似于一個優(yōu)化任務，其目的是制造出完全適合在其環(huán)境中繁衍生息的有機體。

在本文中，我將展示如何在Python中實現(xiàn)一個遺傳算法，在幾個小時內(nèi)“進化”一個收集垃圾的機器人。

[[348489]]

背景

我所遇到的遺傳算法原理最好的教程來自Melanie Mitchell寫的一本關于復雜系統(tǒng)的好書《Complexity: A Guided Tour》。

在其中一個章節(jié)中，Mitchell介紹了一個名叫Robby的機器人，他在生活中的唯一目的是撿垃圾，并描述了如何使用GA優(yōu)化Robby的控制策略。下面我將解釋我解決這個問題的方法，并展示如何在Python中實現(xiàn)該算法。有一些很好的包可以用來構造這類算法(比如DEAP)，但是在本教程中，我將只使用基本Python、Numpy和TQDM(可選)。

雖然這只是一個玩具的例子，但GAs在許多實際應用中都有使用。作為一個數(shù)據(jù)科學家，我經(jīng)常用它們來進行超參數(shù)優(yōu)化和模型選擇。雖然GAs的計算成本很高，但GAs允許我們并行地探索搜索空間的多個區(qū)域，并且在計算梯度時是一個很好的選擇。

問題描述

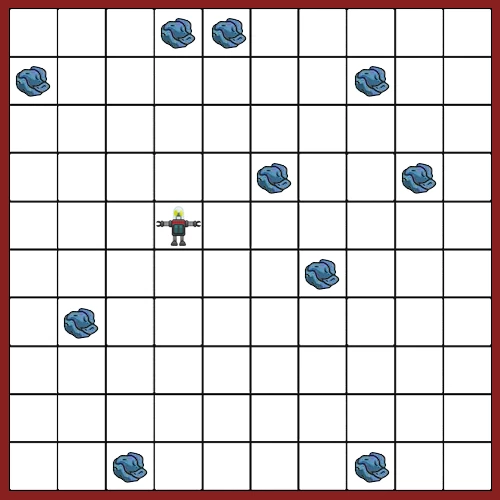
一個名為Robby的機器人生活在一個充滿垃圾的二維網(wǎng)格世界中，周圍有4堵墻(如下圖所示)。這個項目的目標是發(fā)展一個最佳的控制策略，使他能夠有效地撿垃圾，而不是撞墻。

Robby只能看到他周圍上下左右四個方塊以及他所在的方塊，每個方塊有3個選擇，空的，有垃圾，或者是一面墻。因此，Robby有3⁵=243種不同的情況。Robby可以執(zhí)行7種不同的動作：上下左右的移動(4種)、隨機移動、撿拾垃圾或靜止不動。

因此，Robby的控制策略可以編碼為一個“DNA”字符串，由0到6之間的243位數(shù)字組成(對應于Robby在243種可能的情況下應該采取的行動)。

方法

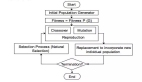
任何GA的優(yōu)化步驟如下：

1. 生成問題初始隨機解的“種群”
2. 個體的“擬合度”是根據(jù)它解決問題的程度來評估的
3. 最合適的解決方案進行“繁殖”并將“遺傳”物質傳遞給下一代的后代
4. 重復第2步和第3步，直到我們得到一組優(yōu)化的解決方案

在我們的任務中，你創(chuàng)建了第一代Robbys初始化為隨機DNA字符串(對應于隨機控制策略)。然后模擬讓這些機器人在隨機分配的網(wǎng)格世界中運行，并觀察它們的性能。

擬合度

機器人的擬合度取決于它在n次移動中撿到多少垃圾，以及它撞到墻上多少次。在我們的例子中，機器人每撿到一塊垃圾就給它10分，每次它撞到墻上就減去5分。然后，這些機器人以它們的擬合度相關的概率進行“交配”(即，撿起大量垃圾的機器人更有可能繁衍后代)，新一代機器人誕生了。

交配

有幾種不同的方法可以實現(xiàn)“交配”。在Mitchell的版本中，她將父母的兩條DNA鏈隨機拼接，然后將它們連接在一起，為下一代創(chuàng)造一個孩子。在我的實現(xiàn)中，我從每一個親本中隨機分配每個基因(即，對于243個基因中的每一個，我擲硬幣決定遺傳誰的基因)。

例如使用我的方法，在前10個基因里，父母和孩子可能的基因如下： 

Parent 1: 1440623161 
Parent 2: 2430661132 
Child:    2440621161 

突變

我們用這個算法復制的另一個自然選擇的概念是“變異”。雖然一個孩子的絕大多數(shù)基因都是從父母那里遺傳下來的，但我也建立了基因突變的小可能性(即隨機分配)。這種突變率使我們能夠探索新的可能。

Python實現(xiàn)

第一步是導入所需的包并為此任務設置參數(shù)。我已經(jīng)選擇了這些參數(shù)作為起點，但是它們可以調整，我鼓勵你可以嘗試調整。 

""" 
導入包 
""" 
import numpy as np 
from tqdm.notebook import tqdm 
 
""" 
設置參數(shù) 
""" 
# 仿真設置 
pop_size = 200 # 每一代機器人的數(shù)量 
num_breeders = 100 # 每一代能夠交配的機器人數(shù)量 
num_gen = 400 # 總代數(shù) 
iter_per_sim = 100 # 每個機器人垃圾收集模擬次數(shù) 
moves_per_iter = 200 # 機器人每次模擬可以做的移動數(shù) 
 
# 網(wǎng)格設置 
rubbish_prob = 0.5 # 每個格子中垃圾的概率 
grid_size = 10 # 0網(wǎng)格大小(墻除外) 
 
# 進化設置 
wall_penalty = -5 # 因撞到墻上而被扣除的擬合點 
no_rub_penalty = -1 # 在空方塊撿垃圾被扣分 
rubbish_score = 10 # 撿垃圾可獲得積分 
mutation_rate = 0.01 # 變異的概率 

接下來，我們?yōu)榫W(wǎng)格世界環(huán)境定義一個類。我們用標記“o”、“x”和“w”來表示每個單元，分別對應一個空單元、一個帶有垃圾的單元和一個墻。 

class Environment: 
    """ 
    類，用于表示充滿垃圾的網(wǎng)格環(huán)境。每個單元格可以表示為: 
    'o': 空 
    'x': 垃圾 
    'w': 墻 
    """ 
    def __init__(self, p=rubbish_prob, g_size=grid_size): 
        self.p = p # 單元格是垃圾的概率 
        self.g_size = g_size # 不包括墻 
 
        # 初始化網(wǎng)格并隨機分配垃圾 
        self.grid = np.random.choice(['o','x'], size=(self.g_size+2,self.g_size+2), p=(1 - self.p, self.p)) 
         
        # 設置外部正方形為墻壁 
        self.grid[:,[0,self.g_size+1]] = 'w' 
        self.grid[[0,self.g_size+1], :] = 'w' 
 
    def show_grid(self): 
        # 以當前狀態(tài)打印網(wǎng)格 
        print(self.grid) 
 
    def remove_rubbish(self,i,j): 
        # 從指定的單元格(i,j)清除垃圾 
        if self.grid[i,j] == 'o': # 單元格已經(jīng)是空 
            return False 
        else: 
            self.grid[i,j] = 'o' 
            return True 
 
    def get_pos_string(self,i,j): 
        # 返回一個字符串，表示單元格(i,j)中機器人“可見”的單元格 
        return self.grid[i-1,j] + self.grid[i,j+1] + self.grid[i+1,j] + self.grid[i,j-1] + self.grid[i,j] 

接下來，我們創(chuàng)建一個類來表示我們的機器人。這個類包括執(zhí)行動作、計算擬合度和從一對父機器人生成新DNA的方法。 

class Robot: 
    """ 
    用于表示垃圾收集機器人 
    """ 
    def __init__(self, p1_dna=None, p2_dna=None, m_rate=mutation_rate, w_pen=wall_penalty, nr_pen=no_rub_penalty, r_score=rubbish_score): 
        self.m_rate = m_rate # 突變率 
        self.wall_penalty = w_pen # 因撞到墻上而受罰 
        self.no_rub_penalty = nr_pen # 在空方塊撿垃圾的處罰 
        self.rubbish_score = r_score # 撿垃圾的獎勵 
        self.p1_dna = p1_dna # 父母2的DNA 
        self.p2_dna = p2_dna # 父母2的DNA 
         
        # 生成字典來從場景字符串中查找基因索引 
        con = ['w','o','x'] # 墻，空，垃圾 
        self.situ_dict = dict() 
        count = 0 
        for up in con: 
            for right in con: 
                for down in con: 
                    for left in con: 
                        for pos in con: 
                            self.situ_dict[up+right+down+left+pos] = count 
                            count += 1 
         
        # 初始化DNA 
        self.get_dna() 
 
    def get_dna(self): 
        # 初始化機器人的dna字符串 
        if self.p1_dna is None: 
            # 沒有父母的時候隨機生成DNA 
            self.dna = ''.join([str(x) for x in np.random.randint(7,size=243)]) 
        else: 
            self.dna = self.mix_dna() 
 
    def mix_dna(self): 
        # 從父母的DNA生成機器人的DNA 
        mix_dna = ''.join([np.random.choice([self.p1_dna,self.p2_dna])[i] for i in range(243)]) 
 
        #添加變異 
        for i in range(243): 
            if np.random.rand() > 1 - self.m_rate: 
                mix_dna = mix_dna[:i] + str(np.random.randint(7)) + mix_dna[i+1:] 
 
        return mix_dna 
 
    def simulate(self, n_iterations, n_moves, debug=False): 
        # 仿真垃圾收集 
        tot_score = 0 
        for it in range(n_iterations): 
            self.score = 0 # 擬合度分數(shù) 
            self.envir = Environment() 
            self.i, self.j = np.random.randint(1,self.envir.g_size+1, size=2) # 隨機分配初始位置 
            if debug: 
                print('before') 
                print('start position:',self.i, self.j) 
                self.envir.show_grid() 
            for move in range(n_moves): 
                self.act() 
            tot_score += self.score 
            if debug: 
                print('after') 
                print('end position:',self.i, self.j) 
                self.envir.show_grid() 
                print('score:',self.score) 
        return tot_score / n_iterations # n次迭代的平均得分 
 
    def act(self): 
        # 根據(jù)DNA和機器人位置執(zhí)行動作 
        post_str = self.envir.get_pos_string(self.i, self.j) # 機器人當前位置 
        gene_idx = self.situ_dict[post_str] # 當前位置DNA的相關索引 
        act_key = self.dna[gene_idx] # 從DNA中讀取行動 
        if act_key == '5': 
            # 隨機移動 
            act_key = np.random.choice(['0','1','2','3']) 
 
        if act_key == '0': 
            self.mv_up() 
        elif act_key == '1': 
            self.mv_right() 
        elif act_key == '2': 
            self.mv_down() 
        elif act_key == '3': 
            self.mv_left() 
        elif act_key == '6': 
            self.pickup() 
 
    def mv_up(self): 
        # 向上移動 
        if self.i == 1: 
            self.score += self.wall_penalty 
        else: 
            self.i -= 1 
 
    def mv_right(self): 
        # 向右移動 
        if self.j == self.envir.g_size: 
            self.score += self.wall_penalty 
        else: 
            self.j += 1 
 
    def mv_down(self): 
        # 向下移動 
        if self.i == self.envir.g_size: 
            self.score += self.wall_penalty 
        else: 
            self.i += 1 
 
    def mv_left(self): 
        # 向左移動 
        if self.j == 1: 
            self.score += self.wall_penalty 
        else: 
            self.j -= 1 
 
    def pickup(self): 
        # 撿垃圾 
        success = self.envir.remove_rubbish(self.i, self.j) 
        if success: 
            # 成功撿到垃圾 
            self.score += self.rubbish_score 
        else: 
            # 當前方塊沒有撿到垃圾 
            self.score += self.no_rub_penalty 

最后是運行遺傳算法的時候了。在下面的代碼中，我們生成一個初始的機器人種群，讓自然選擇來運行它的過程。我應該提到的是，當然有更快的方法來實現(xiàn)這個算法(例如利用并行化)，但是為了本教程的目的，我犧牲了速度來實現(xiàn)清晰。 

# 初始種群 
pop = [Robot() for x in range(pop_size)] 
results = [] 
 
# 執(zhí)行進化 
for i in tqdm(range(num_gen)): 
    scores = np.zeros(pop_size) 
     
    # 遍歷所有機器人 
    for idx, rob in enumerate(pop): 
        # 運行垃圾收集模擬并計算擬合度 
        score = rob.simulate(iter_per_sim, moves_per_iter) 
        scores[idx] = score 
 
    results.append([scores.mean(),scores.max()]) # 保存每一代的平均值和最大值 
 
    best_robot = pop[scores.argmax()] # 保存最好的機器人 
 
    # 限制那些能夠交配的機器人的數(shù)量 
    inds = np.argpartition(scores, -num_breeders)[-num_breeders:] # 基于擬合度得到頂級機器人的索引 
    subpop = [] 
    for idx in inds: 
        subpop.append(pop[idx]) 
    scores = scores[inds] 
 
    # 平方并標準化 
    norm_scores = (scores - scores.min()) ** 2  
    norm_scores = norm_scores / norm_scores.sum() 
 
    # 創(chuàng)造下一代機器人 
    new_pop = [] 
    for child in range(pop_size): 
        # 選擇擬合度優(yōu)秀的父母 
        p1, p2 = np.random.choice(subpop, p=norm_scores, size=2, replace=False) 
        new_pop.append(Robot(p1.dna, p2.dna)) 
 
    pop = new_pop 

雖然最初大多數(shù)機器人不撿垃圾，總是撞到墻上，但幾代人之后，我們開始看到一些簡單的策略(例如“如果與垃圾在一起，就撿起來”和“如果挨著墻，就不要移到墻里”)。經(jīng)過幾百次的反復，我們只剩下一代不可思議的垃圾收集天才!

結果

下面的圖表表明，我們能夠在400代機器人種群中“進化”出一種成功的垃圾收集策略。 

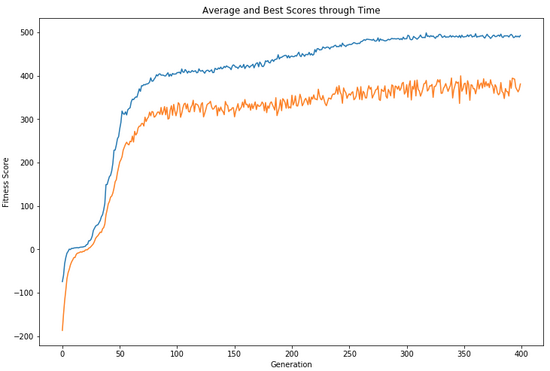
為了評估進化控制策略的質量，我手動創(chuàng)建了一個基準策略，其中包含一些直觀合理的規(guī)則：

• 如果垃圾在當前方塊，撿起來
• 如果在相鄰的方塊上可以看到垃圾，移到那個方塊
• 如果靠近墻，則向相反方向移動
• 否則，隨意移動

平均而言，這一基準策略達到了426.9的擬合度，但我們最終的“進化”機器人的平均擬合度為475.9。

戰(zhàn)略分析

這種優(yōu)化方法最酷的一點是，你可以找到反直覺的解決方案。機器人不僅能夠學習人類可能設計的合理規(guī)則，而且還自發(fā)地想出了人類可能永遠不會考慮的策略。一種先進的技術出現(xiàn)了，就是使用“標記物”來克服近視和記憶不足。

例如，如果一個機器人現(xiàn)在在一個有垃圾的方塊上，并且可以看到東西方方塊上的垃圾，那么一個天真的方法就是立即撿起當前方塊上的垃圾，然后移動到那個有垃圾的方塊。這種策略的問題是，一旦機器人移動(比如向西)，他就無法記住東邊還有1個垃圾。為了克服這個問題，我們觀察了我們的進化機器人執(zhí)行以下步驟：

• 向西移動(在當前方塊留下垃圾作為標記)
• 撿起垃圾往東走(它可以看到垃圾作為標記)
• 把垃圾撿起來，搬到東邊去
• 撿起最后一塊垃圾 

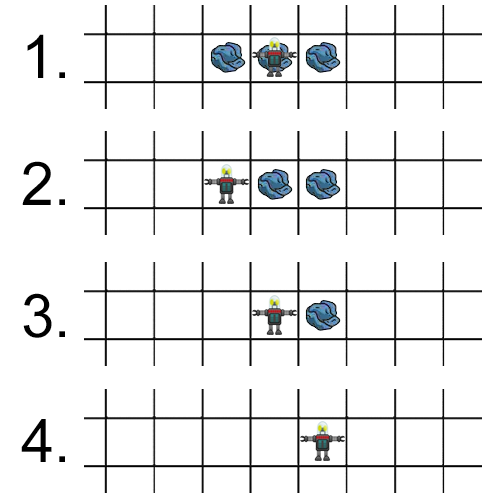
從這種優(yōu)化中產(chǎn)生的另一個反直覺策略的例子如下所示。OpenAI使用強化學習(一種更復雜的優(yōu)化方法)教代理玩捉迷藏。我們看到，這些代理一開始學習“人類”策略，但最終學會了新的解決方案。

結論

遺傳算法以一種獨特的方式將生物學和計算機科學結合在一起，雖然不一定是最快的算法，但在我看來，它們是最美麗的算法之一。