大家好，我是小寒。

今天給大家分享神經網絡中的一個重要知識點，激活函數

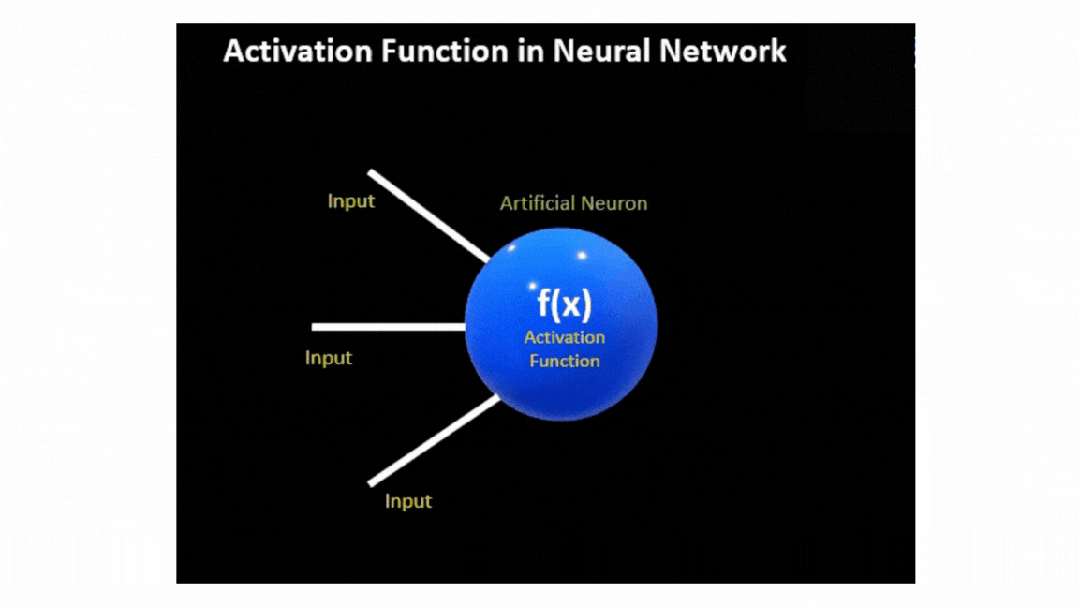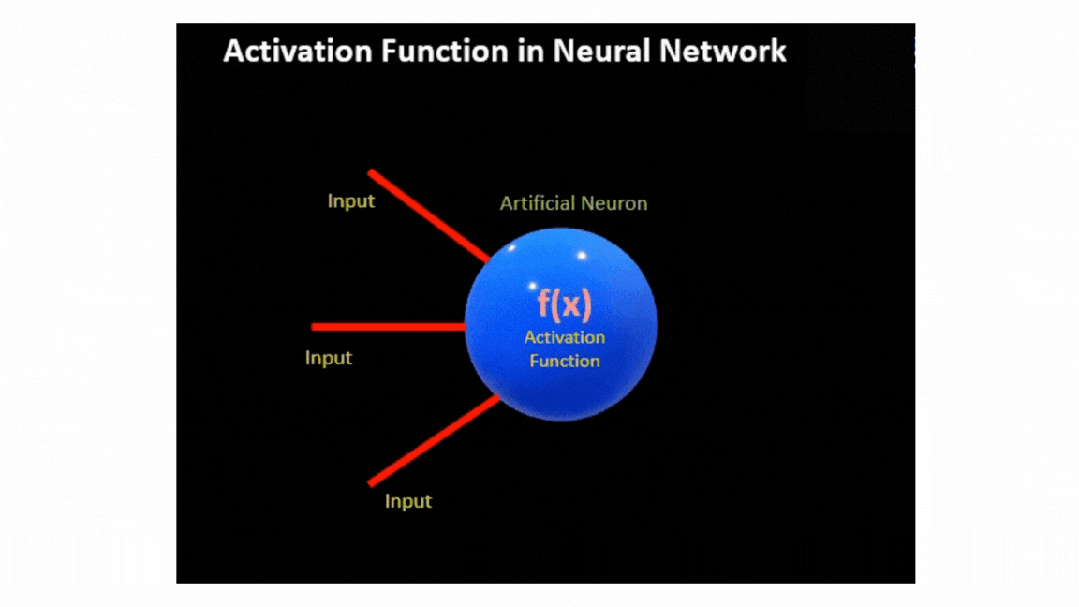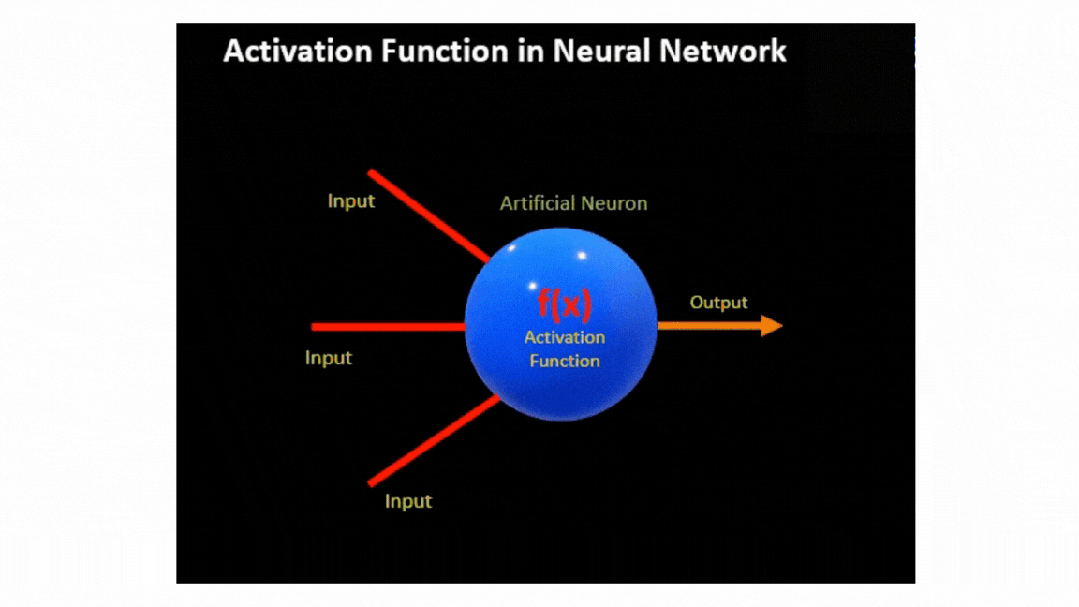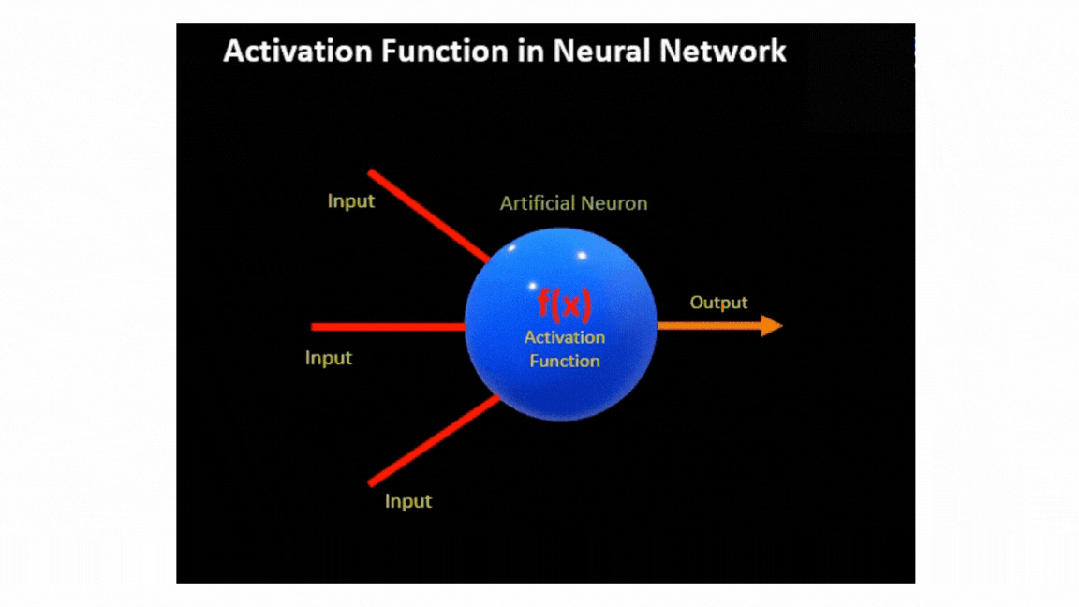
在神經網絡中，激活函數（Activation Function）是神經元計算的一部分，決定了一個神經元在接收到輸入信號后的輸出。

激活函數通過引入非線性特性，使神經網絡能夠學習復雜的模式和表示。

什么是激活函數

激活函數使神經網絡能夠學習和模擬輸入數據和目標變量之間復雜的非線性關系。

通過引入非線性特性，激活函數可以幫助網絡處理涉及復雜函數映射的任務，而這些任務僅靠線性函數無法解決。

圖片

實際上，在神經網絡中，神經元的輸出是通過對輸入特征 X 及其相應權重 W 的乘積加上偏差 b 

然后，將該線性組合傳遞到激活函數 f(x)，從而引入必要的非線性和輸出信號。

現在，這些信號成為后續層的輸入，使網絡能夠構建數據的分層表示。

該機制確保 ANN 能夠從多樣化和非線性的數據分布中進行概括和學習。

常見的激活函數

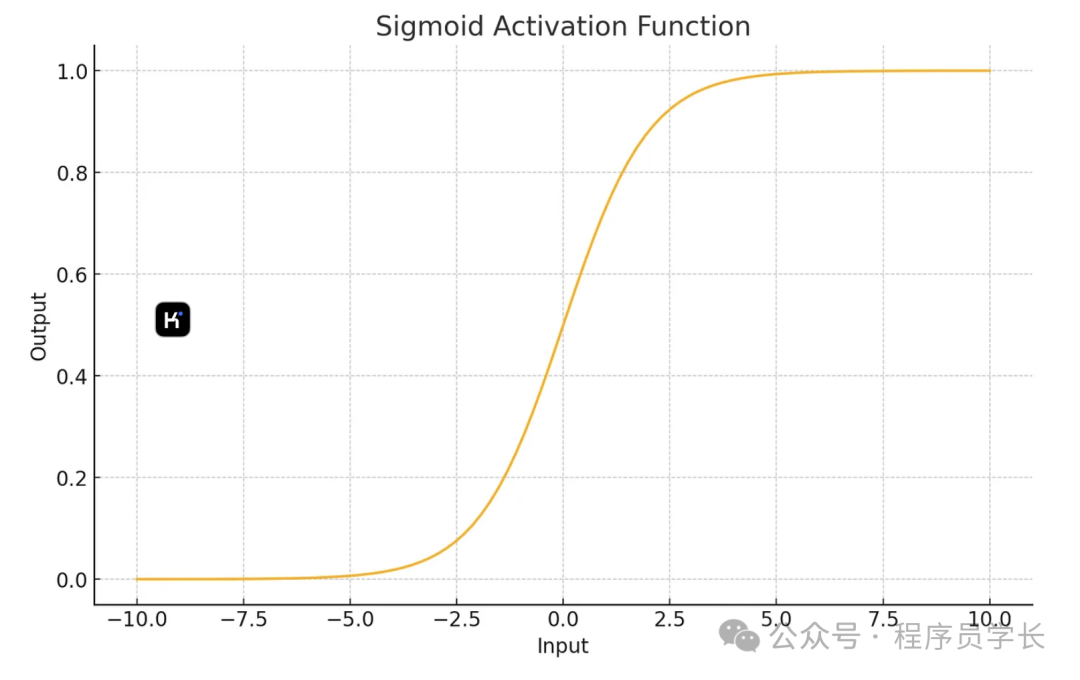
1.Sigmoid 激活函數

Sigmoid 函數的公式為：

圖片

特點：

• 輸出范圍在 (0, 1) 之間。
• 常用于二分類問題的輸出層。
• 有平滑、單調遞增的特性。
• 存在梯度消失問題，尤其在深層網絡中會導致訓練緩慢。

Python實現

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
 return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = sigmoid(x)
plt.plot(x, y)
plt.title("Sigmoid Activation Function")
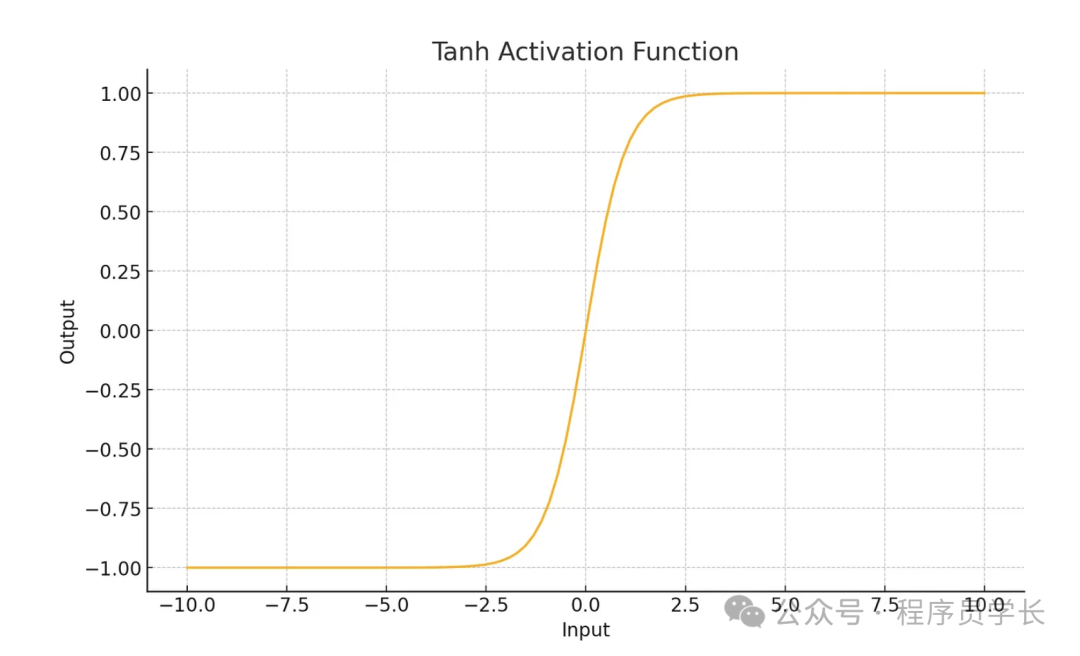
plt.show()

2.Tanh

Tanh（雙曲正切）函數的公式為：

圖片

特點：

• 輸出范圍在 (-1, 1) 之間。
• 比 Sigmoid 更適合深層網絡，因為其輸出均值為 0，使得數據更容易居中。
• 同樣存在梯度消失問題，但比 Sigmoid 稍微好一些。

Python 實現

def tanh(x):
 return np.tanh(x)
y = tanh(x)
plt.plot(x, y)
plt.title("Tanh Activation Function")
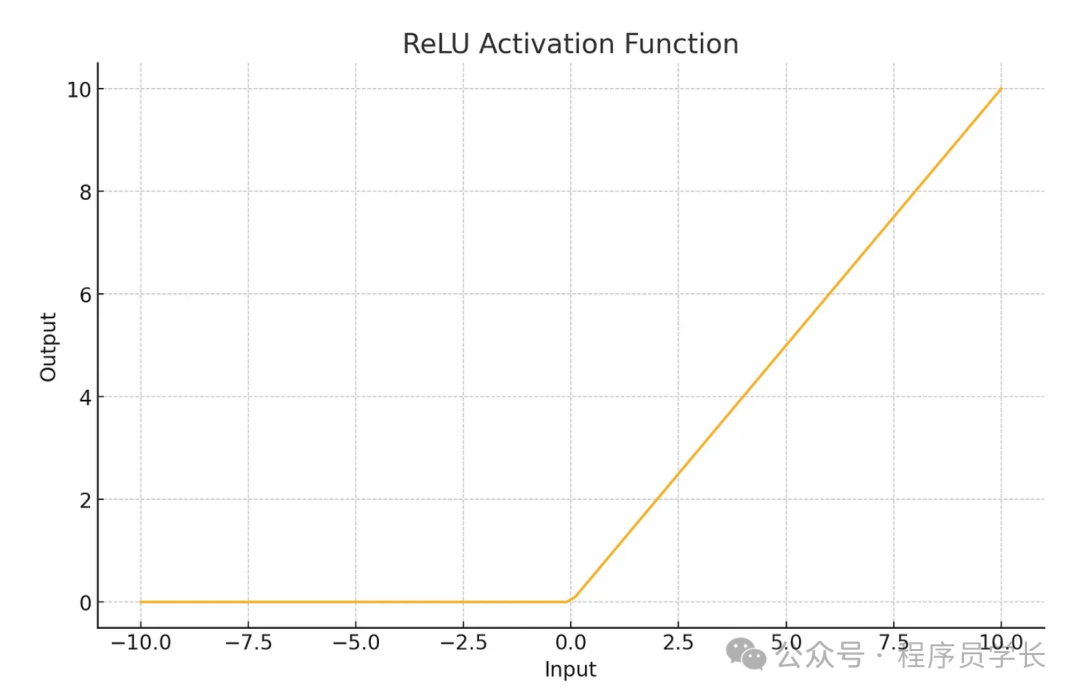
plt.show()

3.ReLU

ReLU（Rectified Linear Unit）函數的公式為：

圖片

特點：

• 輸出范圍在 [0, ∞) 之間。
• 計算簡單，收斂速度快，廣泛應用于各種神經網絡中。
• 存在 “死亡 ReLU” 問題，當輸入值為負時，梯度為 0，可能導致神經元不會再被更新。

Python 實現

def relu(x):
 return np.maximum(0, x)
y = relu(x)
plt.plot(x, y)
plt.title("ReLU Activation Function")
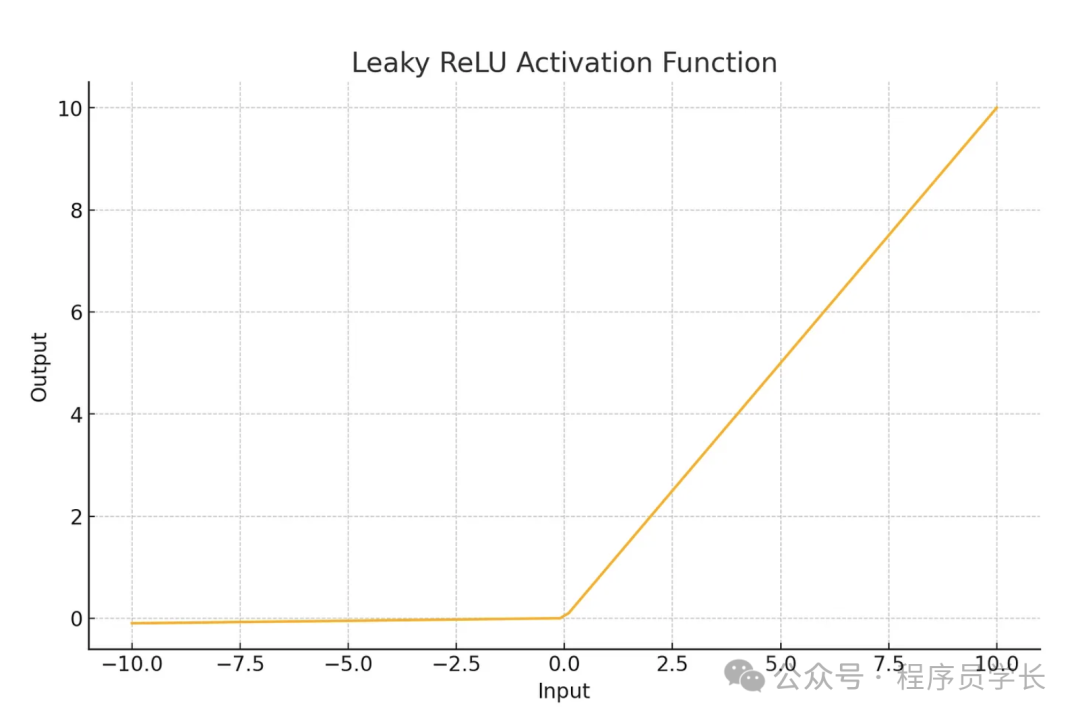
plt.show()

4.Leaky ReLU

Leaky ReLU 是 ReLU 的變種，允許負值通過一個很小的斜率，公式為

圖片

特點

• 解決了 ReLU 函數中神經元“死亡”的問題。
• 允許少量的負值梯度流過，從而保持神經元的更新。

python 實現

def leaky_relu(x, alpha=0.01):
 return np.where(x > 0, x, alpha * x)
y = leaky_relu(x)
plt.plot(x, y)
plt.title("Leaky ReLU Activation Function")
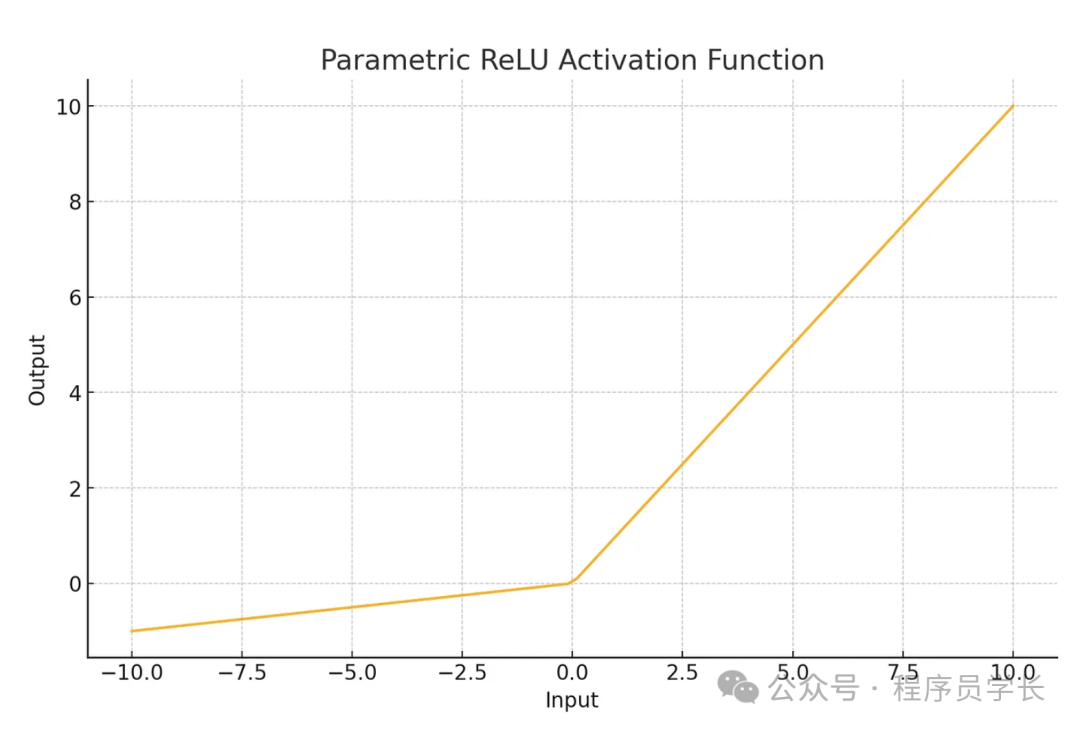
plt.show()

5.PReLU

其公式為

圖片

特點

• 是 Leaky ReLU 的推廣，其中  是一個可訓練的參數。
• 更靈活，能適應不同的數據分布。

Python實現

def prelu(x, alpha):
 return np.where(x > 0, x, alpha * x)
alpha = 0.1 # This would be learned during training
y = prelu(x, alpha)
plt.plot(x, y)
plt.title("Parametric ReLU Activation Function")
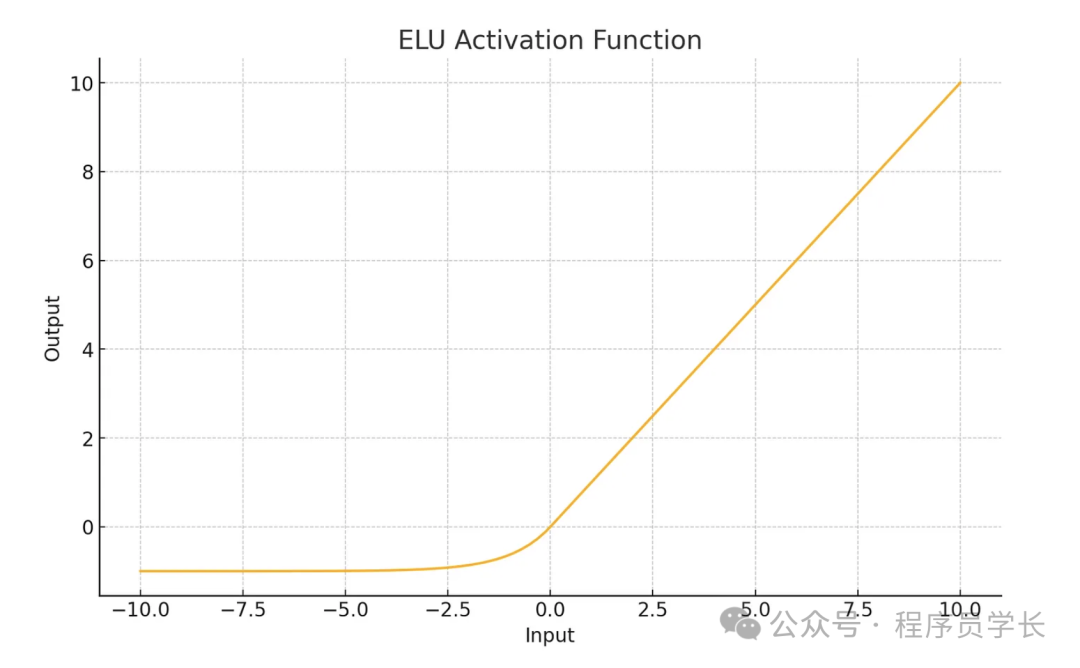
plt.show()

6.ELU

其公式為

圖片

特點

• 當 x > 0 時，ELU 的行為與 ReLU 類似，輸出為 x 本身。
• 當 x ≤ 0 時，ELU 輸出一個負值，形如 ，其中  是一個超參數。
• 負值部分的平滑特性可以使得平均激活接近 0，從而加快收斂速度。
• 相較于 ReLU，ELU 在負值部分具有更好的特性，可以減輕梯度消失問題，同時保留了 ReLU 的大部分優點。

Python 實現

def elu(x, alpha=1.0):
 return np.where(x > 0, x, alpha * (np.exp(x) - 1))
y = elu(x)
plt.plot(x, y)
plt.title("ELU Activation Function")
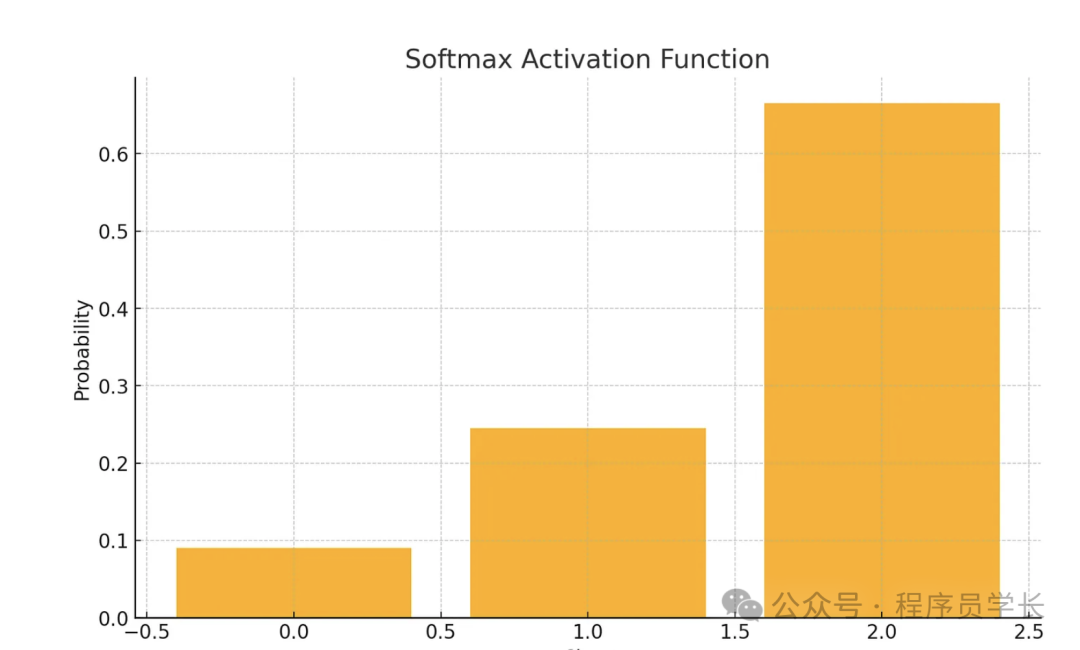
plt.show()

7.Softmax 函數

公式為

圖片

特點

• 常用于多分類問題的輸出層。
• 輸出的是一個概率分布，所有輸出值的和為1。

python 實現

def softmax(x):
 exp_x = np.exp(x-np.max(x))
 return exp_x / exp_x.sum(axis=0)
y = softmax(x)
plt.plot(x, y)
plt.title("Softmax Activation Function")
plt.show()