在剛剛過去的一天，來自清華的光電智能技術交叉創新團隊突破智能光計算訓練難題，相關論文登上 Nature。

論文共同一作是來自清華的薛智威、周天貺，通訊作者是清華的方璐教授、戴瓊海院士。此外，清華電子系徐智昊、之江實驗室虞紹良也參與了這項研究。

• 論文地址：https://www.nature.com/articles/s41586-024-07687-4
• 論文標題：Fully forward mode training for optical neural networks

隨著大模型的規模越來越大，算力需求爆發式增長，就拿 Sora 來說，據爆料，訓練參數量約為 30 億，預計使用了 4200-10500 塊 H100 訓了 1 個月。全球的科技大廠都在高價求購的「卡」，都是硅基的電子芯片。在此之外，還有一種將計算載體從電變為光的光子芯片技術。它們利用光在芯片中的傳播進行計算，具有超高的并行度和速度，被認為是未來顛覆性計算架構最有力的競爭方案之一。

光計算領域也在使用 AI 輔助設計系統。然而，AI 也給光計算技術套上了「瓶頸」—— 光神經網絡訓練嚴重依賴基于數據對光學系統建模的方法。這導致研究人員難以修正實驗誤差。更重要的是，不完善的系統加上光傳播的復雜性，幾乎不可能實現對光學系統的完美建模，離線模型與現實之間總是難以完全同步。

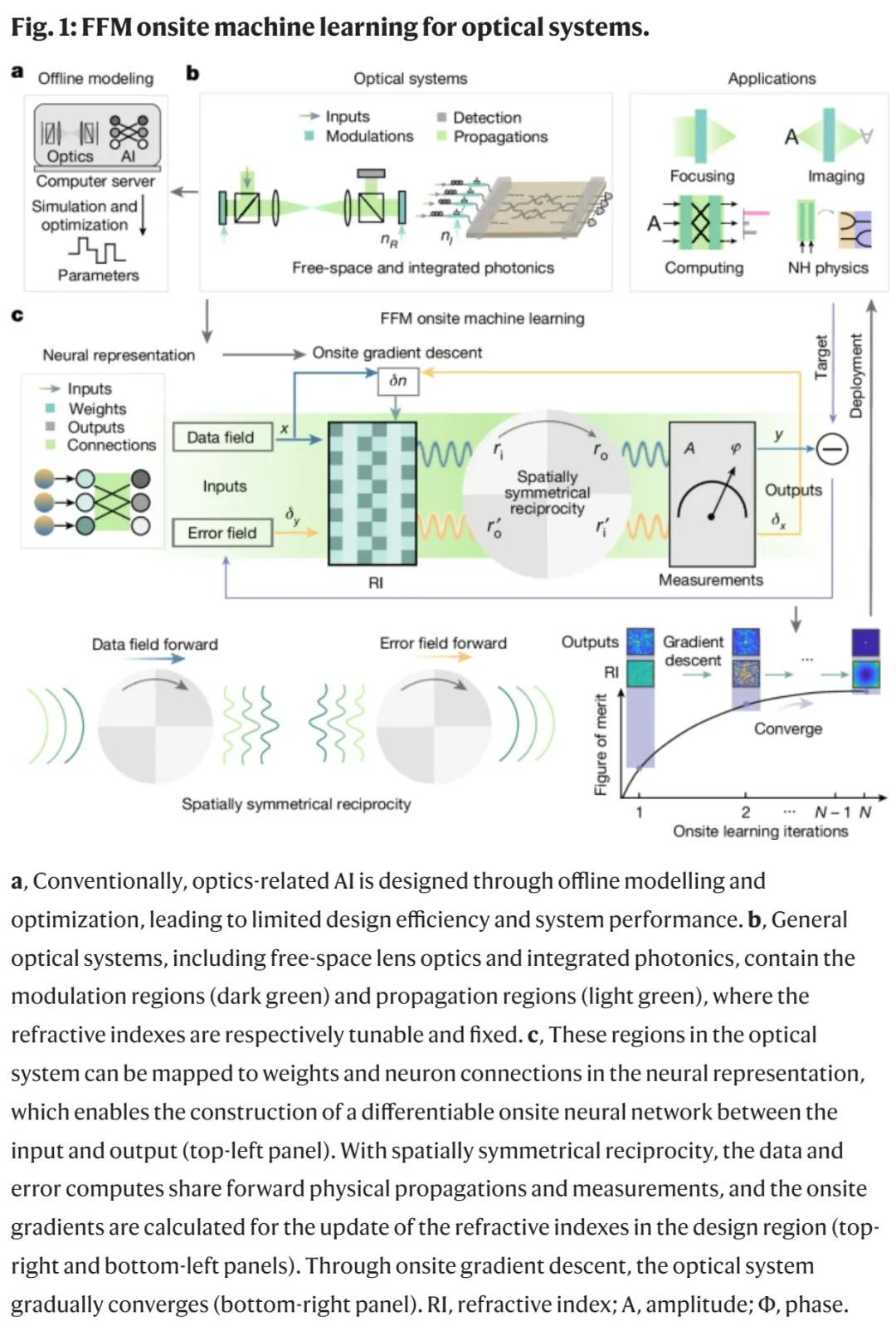
而機器學習常用的「梯度下降」和「反向傳播」，來到了光學領域，也不好使了。為了使基于梯度的方法有效，光學系統必須非常精確地校準和對齊，以確保光信號能夠正確地在系統中反向傳播，離線模型往往很難實現這點。

來自清華大學的研究團隊抓住了光子傳播具有對稱性這一特性，將神經網絡訓練中的前向與反向傳播都等效為光的前向傳播。該研究開發了一種稱為全前向模式（FFM，fully forward mode）學習的方法，研究人員不再需要在計算機模型中建模，可以直接在物理光學系統上設計和調整光學參數，再根據測量的光場數據和誤差，使用梯度下降算法有效地得出最終的模型參數。借助 FFM，大多數機器學習操作都可以有效地并行進行，從而減輕了 AI 對光學系統建模的限制。

FFM 學習表明，訓練具有數百萬個參數的光神經網絡可以達到與理想模型相當的準確率。

此外，該方法還支持通過散射介質進行全光學聚焦，分辨率達到衍射極限；它還可以以超過千赫茲的幀率平行成像隱藏在視線外的物體，并可以在室溫下進行光強弱至每像素亞光子的全光處理。 

最后，研究證明了 FFM 學習可以在沒有分析模型的情況下自動搜索非厄米異常點。FFM 學習不僅有助于將學習過程提高幾個數量級，還可以推動深度神經網絡、超靈敏感知和拓撲光學等應用和理論領域的發展。

深度 ONN 上的并行 FFM 梯度下降

圖 2a 展示了使用 FFM 學習的自由空間 ONN（optical neural networks，光學神經網絡）的自我訓練過程。為了驗證 FFM 學習的有效性，研究者首先使用基準數據集訓練了一個單層 ONN 以進行對象分類。

圖 2b 可視化了在 MNIST 數據集上的訓練結果，可以看到，實驗和理論光場之間的結構相似性指數（SSIM）超過了 0.97，這意味著相似度很高（圖 2c）。值得注意的是，由于系統不完善的原因，光場和梯度的理論結果并不能精準地代表物理結果。因此，這些理論結果不應被視為基本事實。

接下來，研究者探究了用于 Fashion-MNIST 數據集分類的多層 ONN，具體如圖 2d 所示。

通過將層數從 2 層增加到 8 層，他們觀察到，計算機訓練網絡的實驗測試結果平均達到了 44.0% (35.1%)、52.4%（8.8%）、58.4%（18.4%）和 58.8%（5.5%）的準確率（兩倍標準差）。這些結果低于 92.2%、93.8%、96.0% 和 96.0% 的理論準確率。通過 FFM 學習，準確率數值分別提升到了 86.5%、91.0%、92.3% 和 92.5%，接近理想的計算機準確率。

圖 2e 描述了 8 層 ONN 的輸出結果。隨著層數增加，計算機訓練的實驗輸出逐漸偏離目標輸出并最終對對象做出誤分類。相比之外，FFM 設計的網絡可以準確地進行正確分類。除了計算密集型數據和誤傳播之外，損失和梯度計算還可以通過現場光學和電子處理來執行。

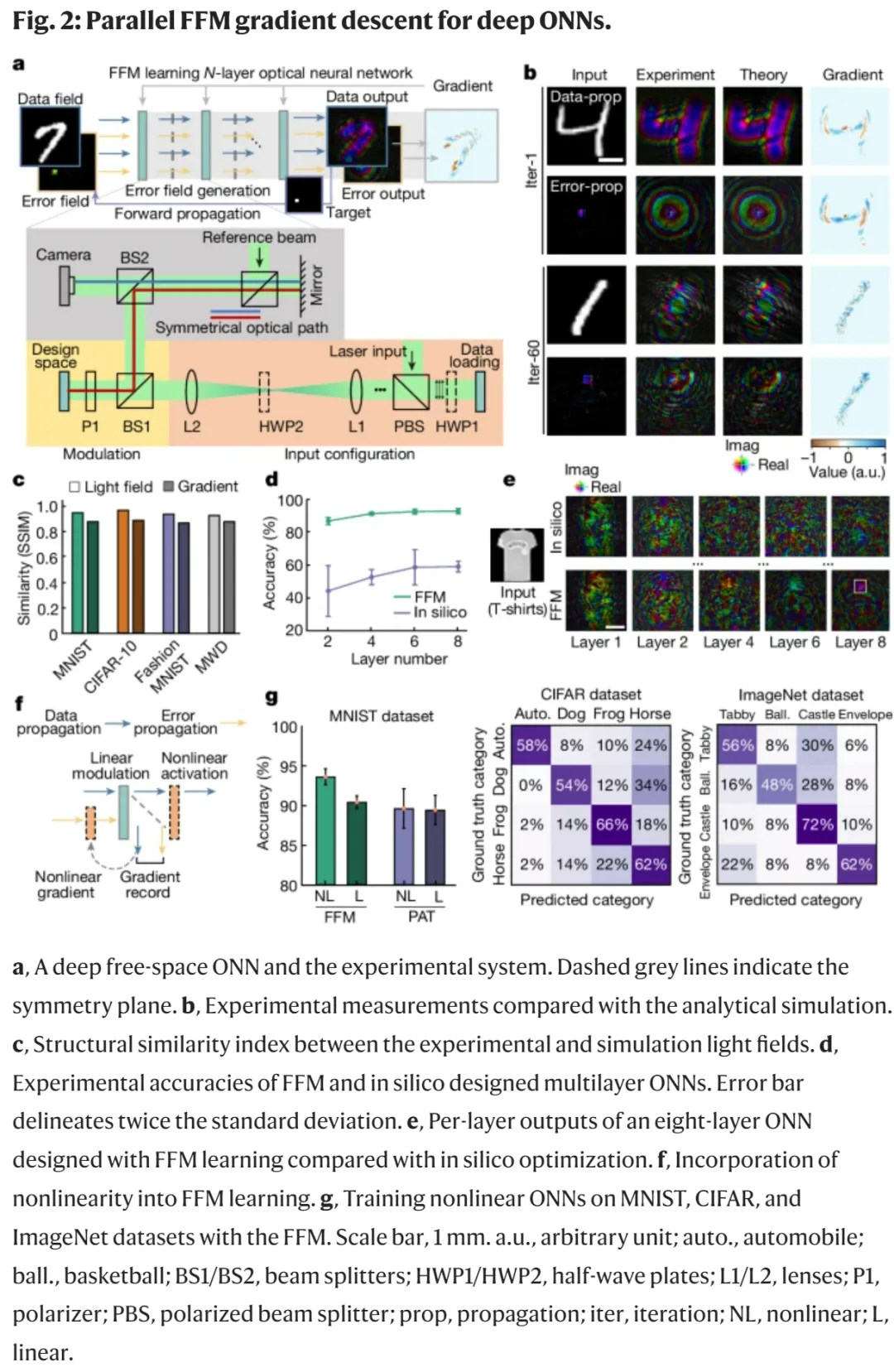
研究者進一步提出了非線性 FFM 學習，如圖 2f 所示。在數據傳播中，輸出在饋入到下一層之前被非線性地激活，記錄非線性激活的輸入并計算相關梯度。在誤差傳播過程中，輸入在傳播之前與梯度相乘。

利用 FFM 進行全光學成像和處理

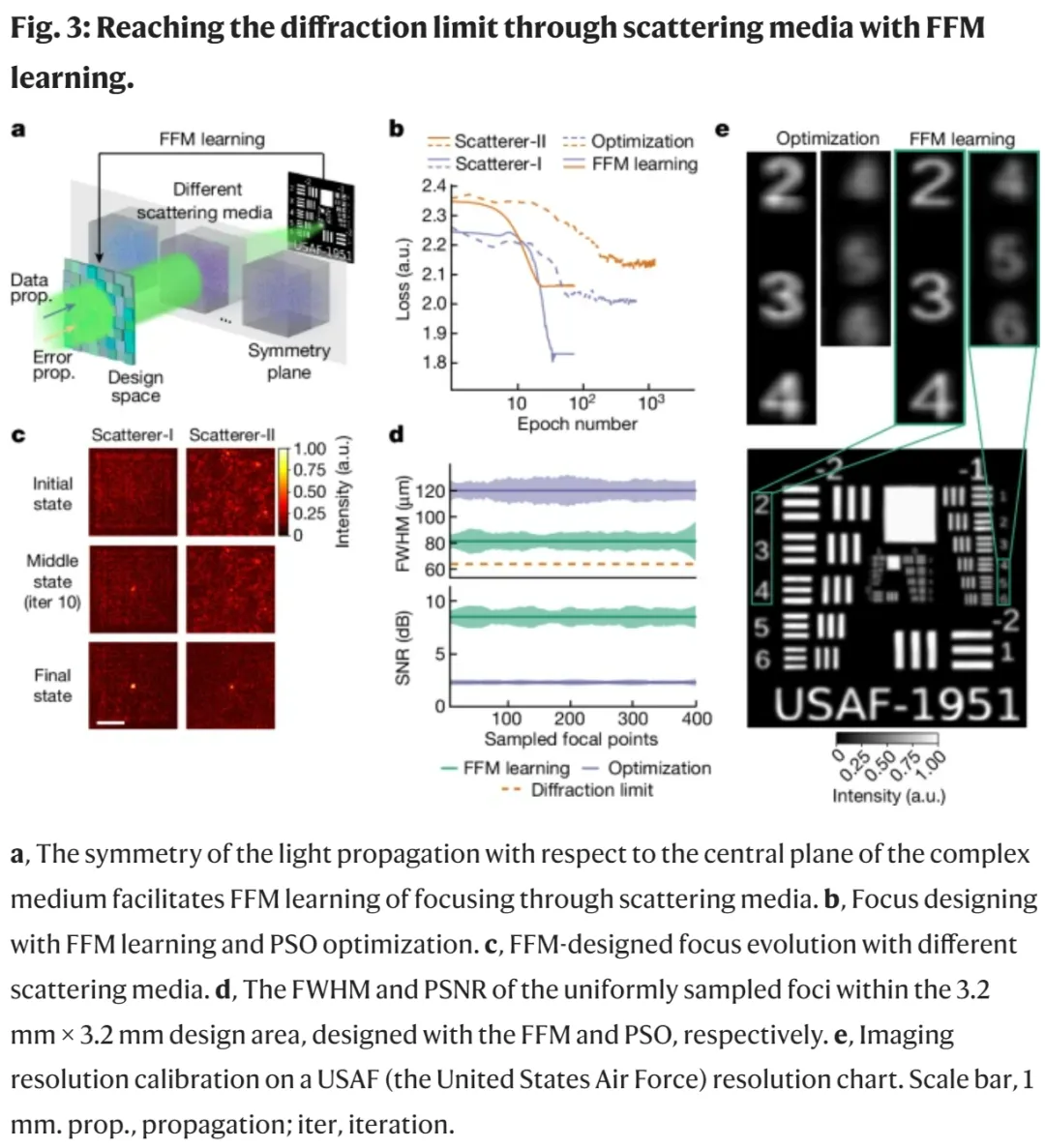
圖 3a 展示了點掃描散射成像系統的實現原理。一般來說，在自適應光學中，啟發式優化方法已經用于焦點優化。

研究者分析了不同的 SOTA 優化方法，并利用粒子群優化（PSO）進行比較，如圖 3b 所示。出于評估的目的，這里采用了兩種不同類型的散射介質，分別是隨機相位板（稱為 Scatterer-I）和透明膠帶（稱為 Scatterer-II）。基于梯度的 FFM 學習表現出更高的效率，在兩種散射介質的實驗中經過 25 次迭代后收斂，收斂損耗值分別為 1.84 和 2.07。相比之下，PSO 方法需要至少 400 次迭代后才能進行收斂，最終損耗值為 2.01 和 2.15。

圖 3c 描述了 FFM 自我設計的演變過程，展示了最開始隨機分布的強度逐漸分布圖逐漸收斂到一個緊密的點，隨后在整個 3.2 毫米 × 3.2 毫米成像區域來學習設計的焦點。

圖 3d 比較了使用 FFM 和 PSO 分別優化的焦點的半峰全寬（FWHM）和峰值信噪比（PSNR）指標。使用 FFM，平均 FWHM 為 81.2 μm，平均 PSNR 為 8.46 dB，最低 FWHM 為 65.6 μm。當使用 3.2mm 寬的方形孔徑和 0.388m 的傳播距離時，通過 FFM 學習設計的焦點尺寸接近衍射極限 64.5 μm。相比之下，PSO 優化產生的 FWHM 為 120.0 μm，PSNR 為 2.29 dB。

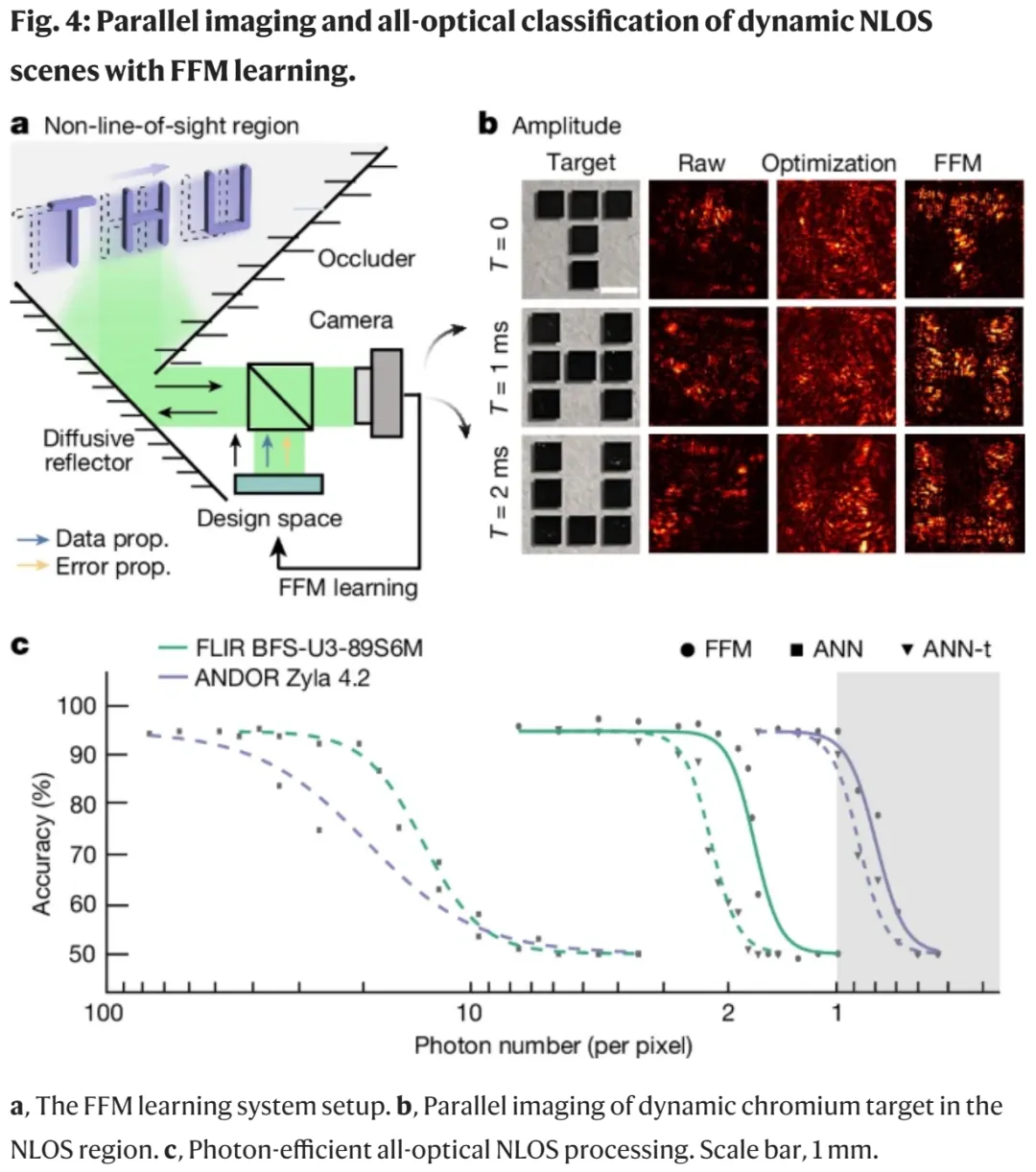
在圖 4a 中，利用往返隱藏對象的光路之間的空間對稱性，FFM 學習可以實現動態隱層對象的全光學現場重建和分析。圖 4b 展示了 NLOS 成像，在學習過程中，輸入波峰被設計用來將對象中所有網格同步映射到它們的目標位置。

現場光子集成電路與 FFM

FFM 學習方法可以推廣到集成光系統的自設計中。圖 5a 展示了 FFM 學習實現過程。其中矩陣的對稱性允許誤差傳播矩陣和數據傳播矩陣之間對等。因此，數據和誤差傳播共享相同的傳播方向。圖 5b 展示了對稱核心實現和封裝芯片實驗的測試設置。

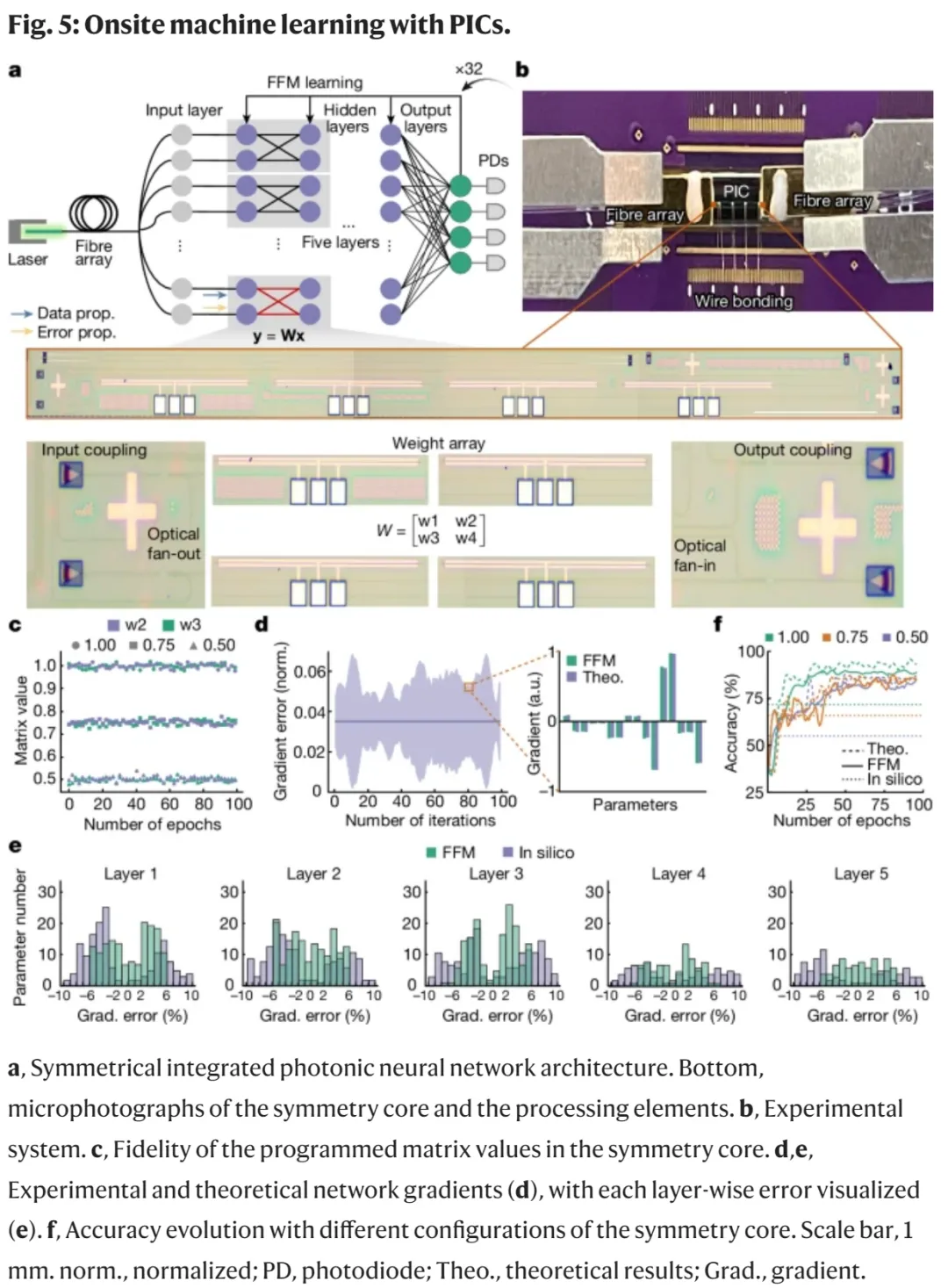
研究者構建的神經網絡用于對鳶尾花（Iris）數據進行分類，輸入處理為 16 × 1 向量，輸出代表三種花的類別之一。訓練期間矩陣編程的保真度如圖 5c 中所示，三個對稱矩陣值的時間漂移分別產生了 0.012%、0.012% 和 0.010% 的標準偏差。

在這種不確定下，研究者將實驗梯度與模擬值進行比較。如圖 5d 所示，實驗梯度與理想模擬值的平均偏差為 3.5%。圖 5d 還說明了第 80 次學習迭代時第二層的設計梯度，而整個神經網絡的誤差在圖 5e 中進行了可視化。在第 80 次迭代中，FFM 學習（計算機模擬訓練）的梯度誤差為 3.50%（5.10%）、3.58%（5.19%）、3.51%（5.24%）、3.56%（5.29%）和 3.46%（5.94%）。設計精度的演變如圖 5f 所示。理想模擬和 FFM 實驗都需要大約 100 個 epoch 才能收斂。在三種對稱率配置下，實驗性能與模擬性能相似，網絡收斂到 94.7%、89.2% 和 89.0% 的準確率。FFM 方法實現了 94.2%、89.2% 和 88.7% 的準確率。相比之下，計算機設計的網絡表現出 71.7%、65.8% 和 55.0% 的實驗準確率。

基于這篇論文的成果，研究團隊也推出了「太極 - II」光訓練芯片。「太極 - II」的研發距離上一代「太極」僅過了 4 個月，相關成果也登上了 Science。

論文鏈接：https://www.science.org/doi/10.1126/science.adl1203

值得一提的是，作為全球首款大規模干涉衍射異構集成芯片的「太極」，其計算能力可以比肩億級神經元的芯片。論文的實驗結果顯示，「太極」的能效是英偉達 H100 的 1000 倍。這種強大的計算能力基于研究團隊首創的分布式廣度智能光計算架構。

更多細節，請參考原論文。