終于把機器學習中的評估指標搞懂了!!
今天給大家分享機器學習中常用的評估指標。

評估指標是用來衡量機器學習模型性能的量化標準,它們幫助我們理解模型在特定任務中的表現。
不同的機器學習任務(如分類、回歸)需要不同的評估指標。通過這些指標,我們可以判斷模型的優劣,優化模型的性能,并在不同模型之間進行比較。
分類任務中的評估指標
1.混淆矩陣
混淆矩陣(Confusion Matrix)是用于評估分類模型性能的工具,特別是在二分類和多分類任務中廣泛使用。
它能夠顯示模型的分類結果與實際情況的詳細對比,幫助我們更清晰地理解模型的錯誤類型和分類的準確性。
混淆矩陣是一個 n×n 的矩陣,n 是類別的數量。對于二分類問題,混淆矩陣是一個 的矩陣,表示模型在不同分類結果上的表現。

- 真陽類(True Positive, TP):模型正確預測為正類的數量。
- 真陰類(True Negative, TN):模型正確預測為負類的數量。
- 假陽性 (False Positive, FP):模型錯誤預測為正類的負類樣本數量(也稱為Type I錯誤)。
- 假陰性(False Negative, FN):模型錯誤預測為負類的正類樣本數量(也稱為Type II錯誤)。
from sklearn.datasets import fetch_openml
from sklearn.model_selection import cross_val_predict
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', as_frame=False, parser = "auto")
X, y = mnist.data, mnist.target
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == '5') # True for 5s, False for all other digits
y_test_5 = (y_test == '5')
sgd_clf = SGDClassifier(random_state=42, verbose=True)
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
cm = confusion_matrix(y_train_5, y_train_pred)
print(cm)
#[[53892 687]
# [ 1891 3530]]2.準確率(Accuracy)
準確率是正確分類的樣本數占總樣本數的比例。
其公式為
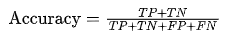
適用場景:適用于類別分布平衡的情況。但對于類別不平衡的問題,準確率可能不夠準確。
3.精確率(Precision)
精確率表示模型預測為正例的樣本中,實際為正例的比例。
其公式為:

適用場景:當關注假正例(FP)影響時,精確率是一個重要的評估指標,如在垃圾郵件過濾中。
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)4.召回率(Recall)
召回率表示所有實際為正例的樣本中,模型正確識別出來的比例。
其公式為
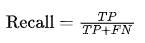
適用場景:當需要盡可能找到所有的正例時(如疾病檢測),召回率是關鍵指標。
recall_score(y_train_5, y_train_pred)5.F1 值(F1-Score)
F1 值是精確率和召回率的調和平均數,用于權衡精確率和召回率之間的關系。
其公式為:
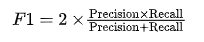
適用場景:當精確率和召回率同等重要時,F1 值是很好的評估標準。
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)6.ROC 曲線和 AUC 值
ROC 曲線展示了分類器的假陽性率(FPR)與真陽性率(TPR)之間的關系。

AUC 值表示 ROC 曲線下面積,AUC 值越大,模型性能越好。AUC 值在0.5到1之間,接近1表示模型性能優異。
適用場景:適用于類別不平衡的分類任務。
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)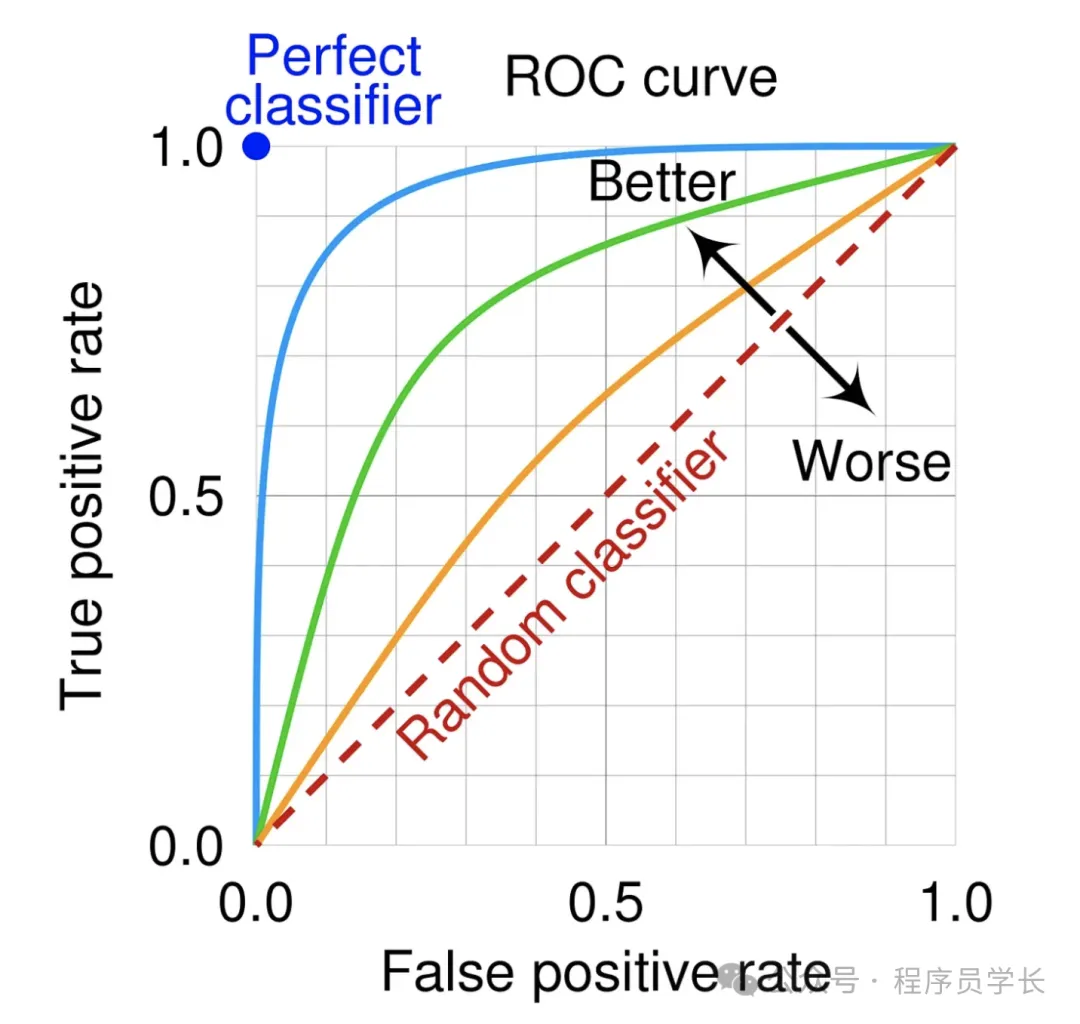
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix, roc_auc_score
# 生成樣本數據
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
model = LogisticRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
y_prob = model.predict_proba(X_test)[:, 1]
# 計算評估指標
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_prob)
conf_matrix = confusion_matrix(y_test, y_pred)
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall: {recall}")
print(f"F1 Score: {f1}")
print(f"ROC AUC Score: {roc_auc}")
print(f"Confusion Matrix:\n{conf_matrix}")回歸問題中的評估指標
1.均方誤差(MSE)
MSE 是模型預測值與真實值差的平方的平均值。它強調大的誤差。
公式:
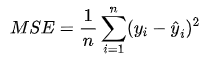
適用場景:適用于回歸任務中,尤其是對大的預測誤差更加敏感的場景。
2.均方根誤差(RMSE)
RMSE 是 MSE 的平方根,用于將誤差帶回與原始目標變量相同的量綱。
公式:
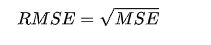
適用場景:與 MSE 類似,但 RMSE 更直觀,誤差與目標變量的尺度一致。
3.平均絕對誤差(MAE)
MAE 是預測值與真實值的絕對差的平均值,較少受大誤差的影響。
公式:
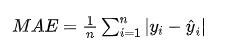
適用場景:當對所有誤差的權重一致,且不希望夸大大誤差影響時,MAE 是較好的指標。
4.R 方值(R2)
R2 衡量模型解釋了多少比例的目標變量方差,其值介于0到1之間。
公式:
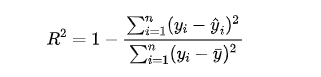
其中, 是目標變量的平均值。
適用場景:用于評估回歸模型的解釋能力。
5.調整 R 方值(Adjusted R2)
在考慮特征數量時,調整后的 R2 對多特征模型的評價更加準確。
公式:
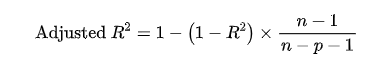
其中, 是模型中的特征數量。
適用場景:在特征數較多時,調整 R2 比普通 R2 更合理。
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 生成樣本數據
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
# 計算評估指標
mse = mean_squared_error(y_test, y_pred)
rmse = mean_squared_error(y_test, y_pred, squared=False) # RMSE is the square root of MSE
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"MSE: {mse}")
print(f"RMSE: {rmse}")
print(f"MAE: {mae}")
print(f"R2: {r2}")











































