AI解決132年數學難題!Transformer成功尋找新的李雅普諾夫函數,三體問題相關
訓練Transformer,用來解決132年的數學世紀難題!
如何判斷一個動力系統(如三體問題)是否穩定?Meta和巴黎理工學院團隊攜手提出Symbolic Transformer,直指這一經典難題的核心:
發現新的全局李雅普諾夫函數。
 圖片
圖片
從牛頓、拉格朗日到龐加萊,無數科學家傾力研究三體問題的長期穩定性,卻始終無法給出一個通用的判定方法。
直到1892年,俄國數學家Aleksandr Lyapunov提出了以他名字命名的李雅普諾夫函數:
如果存在一個函數V,其在平衡點處有嚴格最小值,在無窮遠處為無窮大,且梯度始終指向遠離系統梯度的方向,則全局穩定性得到保證。
但遺憾的是,李雅普諾夫只證明了這個結論,并沒有提供尋找這個函數的方法。
 圖片
圖片
130多年過去了,科學界仍然不知道對于一般的系統該如何尋找李雅普諾夫函數,現有的算法只能求解非常小規模的多項式系統。
換句話說,李雅普諾夫函數的系統化構造方法,依然是一個懸而未決的數學難題。
現在,這一局面有望被AI打破。
 圖片
圖片
研究團隊把尋找李雅普諾夫函數構建成一種序列到序列翻譯任務,問題和解決方案都表示為符號tokens序列,就能用上原本為機器翻譯而生的Transformer模型了。
最終,在8張V100上訓練100個GPU時左右的模型,取得了驚人的成績:
- 對于前人已解決的多項式系統,模型精度高達84%,大幅領先人類專家的9%和此前SOTA算法工具。
- 面對隨機生成的新多項式系統,模型成功找到了10.1%-11.8%的李雅普諾夫函數,而此前最好的算法工具只有0.7%-1.1%。
- 重新發現了Ahmadi等在2011年首次給出的一個多項式系統的非多項式李雅普諾夫函數
相關論文已入選NeurIPS 2024,且剛剛在ArXiv公開。
 圖片
圖片
作者Meta科學家Fran?ois Charto表示,盡管Symbolic Transformer像其他AI模型一樣還是一個黑盒系統,但它給出的李雅普諾夫函數是明確的符號表達式,完全可以經受數學證明的檢驗。
作者巴黎師范數學教授:黑魔法一般的方法
用Transformer解決數學難題,最大的困難是什么?
答案不難想到:缺少數據,特別是在這個場景中,需要動力系統與李雅普諾夫函數的配對數據。
為此,Meta和巴黎理工團隊利用了正向和反向數據生成相結合的策略。
正向數據生成,也就是根據多項式系統生成對應的李雅普諾夫函數。
雖然沒有通用方法,但如果一個李雅普諾夫函數能表示成多項式的平方和,就有現存工具可以計算。
最終方法分為三步:
- 先隨機生成一個多項式系統,
- 尋找是否存在平方和形式的李雅普諾夫函數,
- 如果存在則保留這個多項式系統,不存在回到步驟1
 圖片
圖片
不過這個方法有幾個局限。
大多數對象是系統都不穩定,且計算平方和李雅普諾夫函數涉及復雜的搜索,系統規模的增長,對算力和內存需求會呈爆炸式增長,所以這種方法速度很慢且僅適用于小的多項式系統。
于是還需要配合反向數據生成方法,根據答案反向構造問題。
這種方法也存在幾個局限,比如AI傾向于偷懶,從任務中學習更簡單的子問題,因此也需要做出一些限制。
最終方法大致可以理解成,先隨機生成一個滿足特定條件的李雅普諾夫函數,再反向構造出與之匹配的動力系統。
 圖片
圖片
最終團隊生成了4個數據集:
- BPoly,包含100萬個反向生成的多項式系統與配對的李雅普諾夫函數,系統中的方程數量為2到5個不等。
- BNonPoly,包含100萬個反向生成的非多項式系統配對樣本,現有算法通常無法處理這種類型的系統,非多項式李雅普諾夫函數的發現尤其具有挑戰性
- FBarr,包含30萬個正向生成的Barrier函數配對樣本,并不是嚴格的李雅普諾夫函數,用于測試模型在尋找不能嚴格滿足李雅普諾夫正定條件的系統中的李雅普諾夫函數。
- FLyap,包含10萬個正向生成的標準李雅普諾夫配對樣本,每個動力系統的李雅普諾夫函數都是非齊次多項式,
最終試驗發現,在不同數據集上訓練的模型都取得了很好的準確性。
使用Beam Search方法在寬度50時能給低性能模型帶來額外7%-10%的提升。
 圖片
圖片
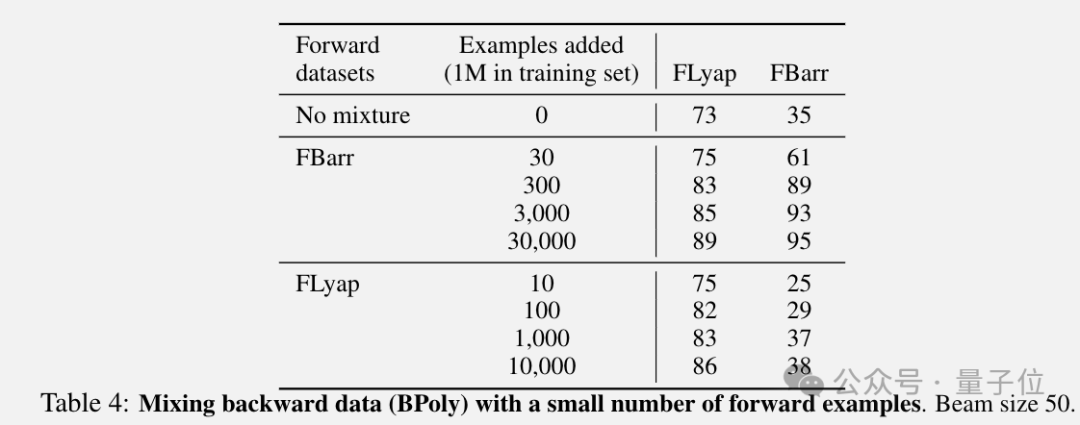
特別是在后向數據訓練集中添加少量前向生成數據示例,帶來顯著的分布外測試性能提升。
將FBarr中的300個示例添加到BPoly中,就能把FBarr準確率從35%提高到89%。另外添加FLyap示例帶來的改進較小。
 圖片
圖片
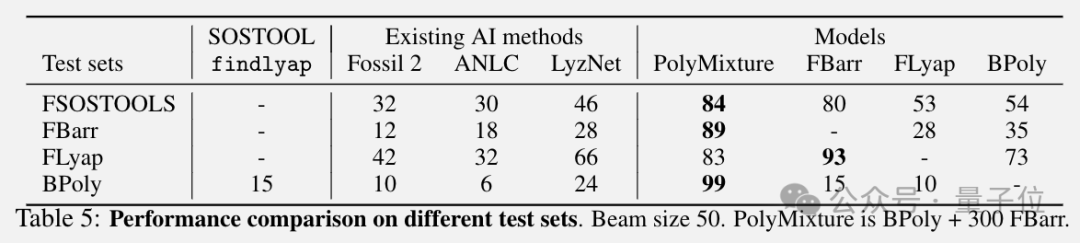
與此前SOTA基線比較,在混合數據上訓練的模型取得了最好的效果。
基于Transformer的模型也比SOSTOOL方法快得多。
當嘗試求解具有2到5個方程的隨機多項式系統時,SOSTOOL的Python版本平均需要 935.2 秒。
Transformer模型在貪婪解碼時,一個系統的推理和驗證平均需要2.6 秒,而Beam Search寬度為50時,平均需要13.9秒。
 圖片
圖片
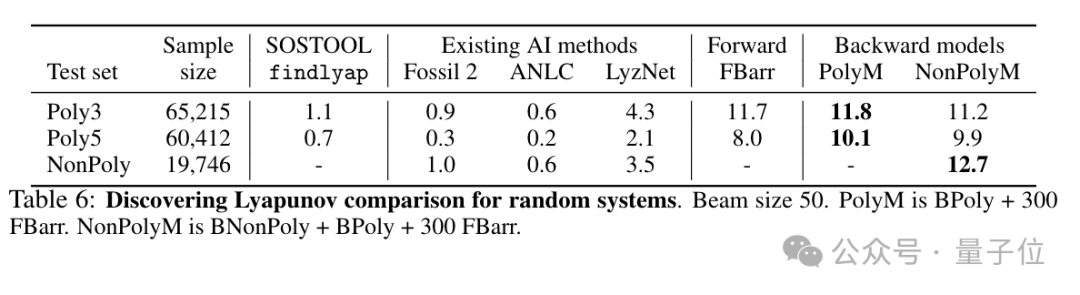
研究的最終目標是發現新的李雅普諾夫函數,在隨機生成的2-3個多項式、2-5個多項式的數據集中,最佳模型發現了11.8%和10.1%的李雅普諾夫函數,是傳統方法的10倍。
對于非多項式系統,模型發現了12.7%的李雅普諾夫函數。
這些結果表明,從合成數據集訓練的語言模型確實可以發現未知的李雅普諾夫函數,并比此前最先進的傳統算法求解器效果更好。
 圖片
圖片
作者巴黎師范教授Amaury Hayat表示,幾年前剛開始這個項目時,作為一個年輕而天真的數學家,他認為如果方法真的成功了,那簡直可以算是黑魔法。
幾年過去了,見識了AI的諸多成就,我對此已經理性得多了,但依然感覺……(不可思議)。
 圖片
圖片
論文地址:https://arxiv.org/abs/2410.08304
參考鏈接:
[1]https://x.com/f_charton/status/1846884416930402633[2]https://x.com/Amaury_Hayat/status/1846889179780673853
— 完 —









































