Python 時序預測常用方法代碼實現
作者：huaan9527
時序預測是根據歷史數據來預測未來一段時間內的數據。Python 中常用的時序預測方法包括：移動平均法（Moving Average, MA）、指數平滑法（Exponential Smoothing, ES）、自回歸模型（Autoregressive Model, AR）、自回歸移動平均模型（Autoregressive Moving Average Model, ARMA）以及自回歸積分移動平均模
時序預測是根據歷史數據來預測未來一段時間內的數據。Python 中常用的時序預測方法包括：移動平均法（Moving Average, MA）、指數平滑法（Exponential Smoothing, ES）、自回歸模型（Autoregressive Model, AR）、自回歸移動平均模型（Autoregressive Moving Average Model, ARMA）以及自回歸積分移動平均模型（Autoregressive Integrated Moving Average Model, ARIMA）。
1. 移動平均法（MA）
移動平均法通過計算一定時間窗口內數據的平均值來進行預測，適用于平穩序列。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.api import SimpleExpSmoothing
# 生成模擬數據
np.random.seed(0)
data = np.random.randn(100).cumsum()
df = pd.DataFrame(data, columns=['value'])
# 檢查數據是否平穩
result = adfuller(df['value'])
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
# 繪制原始數據
df.plot()
plt.title('原始數據')
plt.show()
# 創建移動平均模型
window_size = 5
df['moving_average'] = df['value'].rolling(window=window_size).mean()
# 預測下一輪數據
last_window = df['value'][-window_size:].values
forecast = np.mean(last_window)
print(f"下一個時間點的預測值: {forecast}")
# 繪制預測結果
plt.figure(figsize=(12, 6))
plt.plot(df['value'], label='原始數據')
plt.plot(df['moving_average'], label='移動平均值', color='orange')
plt.axhline(y=forecast, color='red', linestyle='--', label='預測值')
plt.legend()
plt.title('移動平均法預測')
plt.show()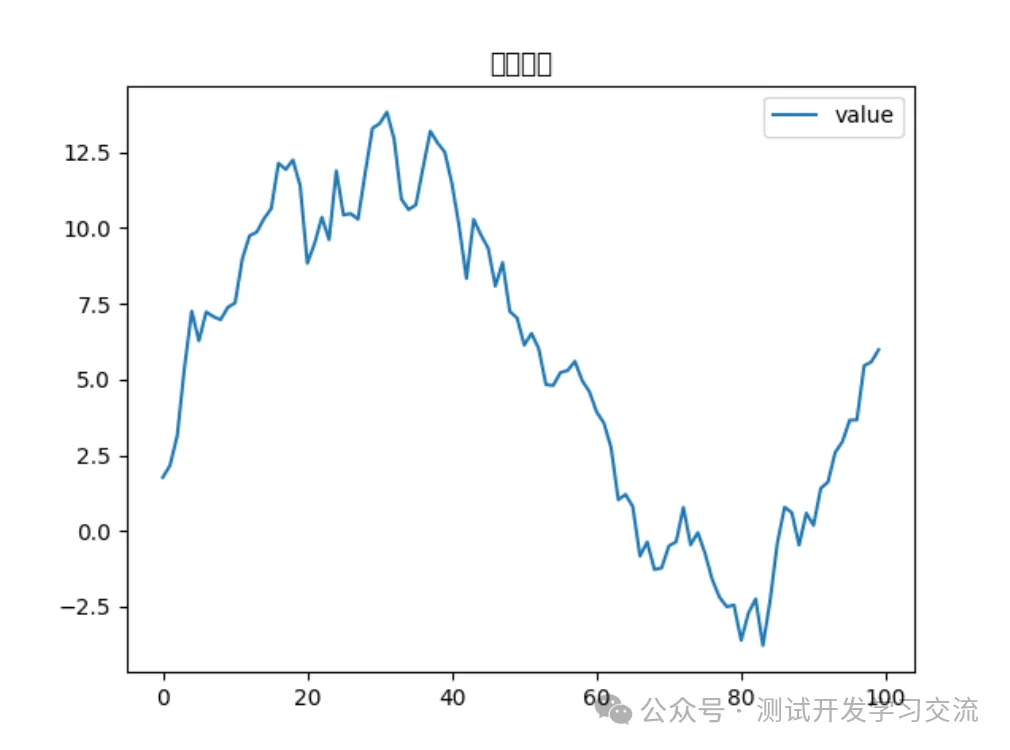
2. 指數平滑法（ES）
指數平滑法通過對歷史數據賦予不同的權重，距離預測點越近的數據權重越大，適用于非平穩序列。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# 生成模擬數據：正弦波加上隨機噪聲
np.random.seed(42)
dates = pd.date_range('20230101', periods=100)
data = np.sin(np.linspace(0, 2 * np.pi, 100)) + np.random.normal(0, 0.1, 100)
df = pd.DataFrame(data, index=dates, columns=['Value'])
# 定義并擬合指數平滑模型
model_es = ExponentialSmoothing(df['Value'], trend='add', seasnotallow='add', seasonal_periods=4)
fit_model_es = model_es.fit()
# 預測下一輪數據
forecast_es = fit_model_es.forecast(5)
# 畫圖展示原始數據和預測結果
plt.figure(figsize=(12, 6))
plt.plot(df['Value'], label='原始數據')
plt.plot(fit_model_es.fittedvalues, label='擬合值', color='green')
plt.plot(forecast_es, label='預測值', color='red')
plt.legend()
plt.title('指數平滑法預測')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()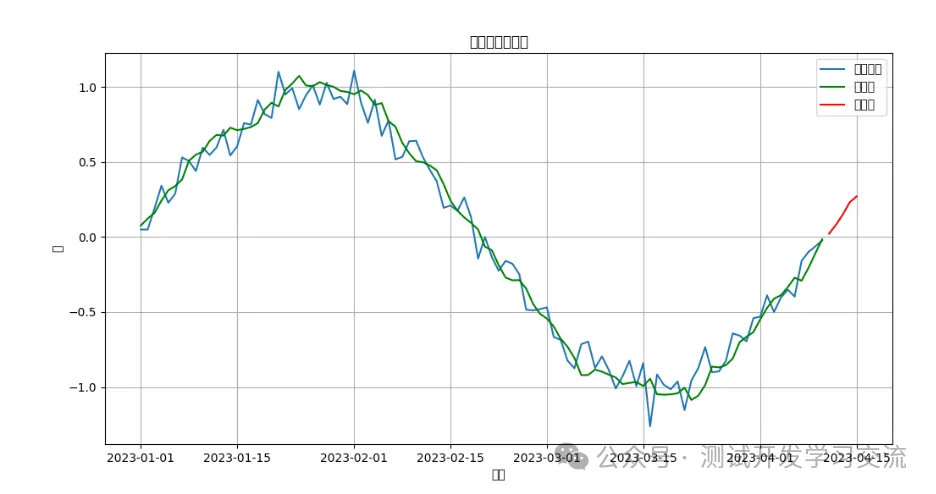
3. 自回歸模型（AR）
自回歸模型是一種線性預測模型，它使用時間序列的過去值作為未來值的預測因子。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 生成自回歸過程的模擬數據
from statsmodels.tsa.arima_process import ArmaProcess
np.random.seed(42)
ar_params = [0.8]
arma_process = ArmaProcess(ar=ar_params)
simulated_data = arma_process.generate_sample(nsample=250)
dates = pd.date_range('20230101', periods=250)
df_arma = pd.Series(simulated_data, index=dates)
# 定義ARIMA模型，這里p=1表示一階自回歸
model_ar = ARIMA(df_arma, order=(1, 0, 0))
# 擬合模型
model_ar_fit = model_ar.fit()
# 進行預測，預測未來10個時間點的數據
forecast_ar = model_ar_fit.forecast(steps=10)
# 畫圖展示原始數據和預測結果
plt.figure(figsize=(12, 6))
plt.plot(df_arma, label='歷史數據')
plt.plot(pd.date_range(dates[-1], periods=10, freq='D'), forecast_ar, label='預測值', color='red')
plt.legend()
plt.title('自回歸模型預測')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()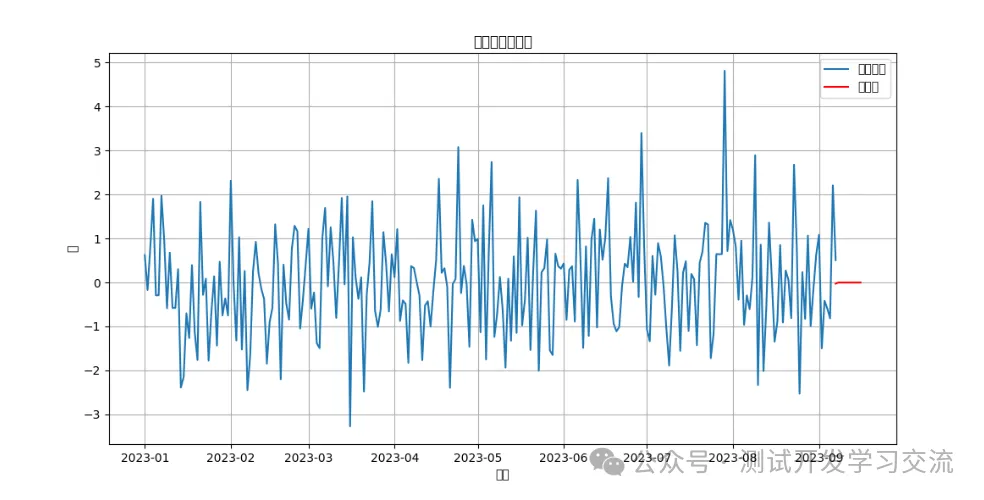
4. 自回歸移動平均模型（ARMA）
ARMA模型結合了AR和MA模型的特點，使用時間序列的過去值和誤差項的過去值作為未來值的預測因子。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import arma_generate_sample
from statsmodels.tsa.arima.model import ARIMA
# 生成ARMA過程的模擬數據
np.random.seed(42)
ar_params = [1, -0.5]
ma_params = [0.7, -0.3]
dates_arma = pd.date_range('20230101', periods=100)
arma_data = arma_generate_sample(nsample=100, ar=ar_params, ma=ma_params)
df_arma = pd.Series(arma_data, index=dates_arma, name='Value_ARMA')
# 定義并擬合ARMA模型
model_arma = ARIMA(df_arma, order=(1, 0, 2))
fit_model_arma = model_arma.fit()
# 預測下一輪數據
forecast_arma = fit_model_arma.predict(start=len(df_arma), end=len(df_arma)+4, typ='levels')
# 畫圖展示原始數據和ARMA預測結果
plt.figure(figsize=(12, 6))
plt.plot(df_arma, label='原始數據')
plt.plot(forecast_arma, label='預測值', color='purple')
plt.legend()
plt.title('ARMA模型預測')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()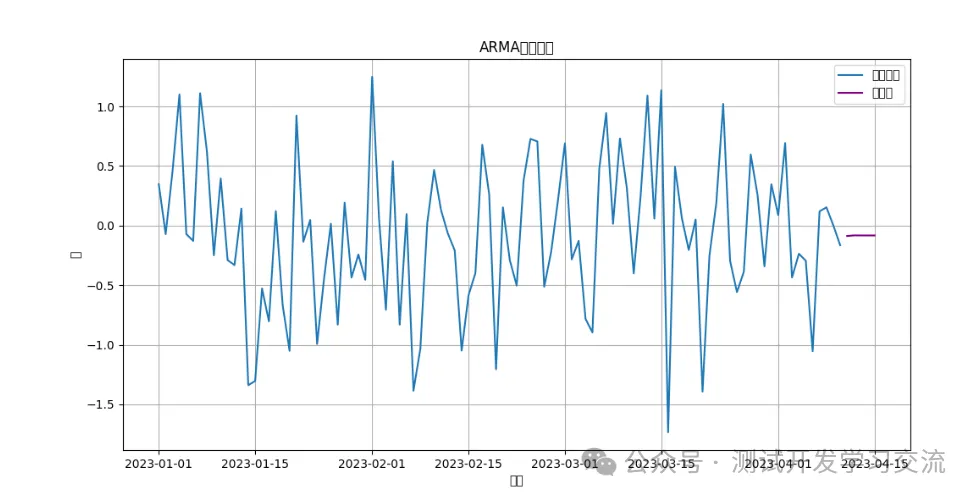
5. 自回歸積分移動平均模型（ARIMA）
ARIMA模型是在ARMA模型的基礎上增加了差分操作，使得非平穩序列可以通過差分變為平穩序列。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
# 生成非平穩的模擬數據
np.random.seed(42)
data = np.random.randn(100).cumsum()
df = pd.DataFrame(data, columns=['value'])
# 定義ARIMA模型，這里p=1, d=1, q=1
model_arima = ARIMA(df['value'], order=(1, 1, 1))
# 擬合模型
model_arima_fit = model_arima.fit()
# 進行預測，預測未來10個時間點的數據
forecast_arima = model_arima_fit.forecast(steps=10)
# 畫圖展示原始數據和預測結果
plt.figure(figsize=(12, 6))
plt.plot(df['value'], label='歷史數據')
plt.plot(pd.date_range(df.index[-1], periods=10, freq='D'), forecast_arima, label='預測值', color='red')
plt.legend()
plt.title('ARIMA模型預測')
plt.xlabel('日期')
plt.ylabel('值')
plt.grid(True)
plt.show()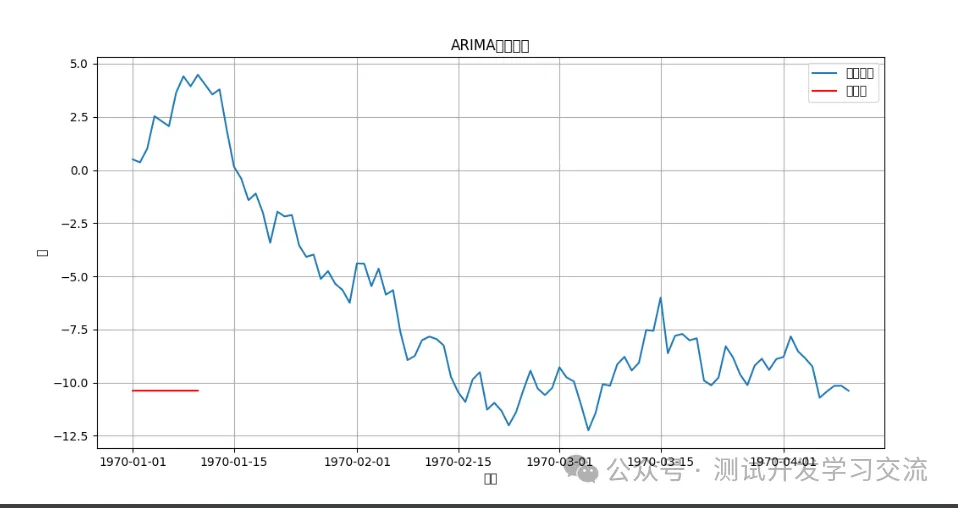
注意事項
選擇合適的預測方法：根據數據的特點和需求選擇合適的預測方法，如平穩序列可以選擇AR、MA或ARMA等，非平穩序列可以選擇ARIMA等。
數據預處理：在進行時序預測之前，需要對數據進行預處理，如去除異常值、填充缺失值等。
參數調整：在實際應用中，可能需要調整模型的參數以獲得更好的預測效果，如調整移動平均的時間窗口大小、指數平滑的平滑系數、ARIMA模型的階數等。
模型診斷：通過殘差分析、AIC/BIC等指標來評估模型的性能，并進行必要的調整。
總結
時序預測是數據分析中的一個重要領域，Python 提供了豐富的庫和工具來實現各種時序預測方法。本文詳細介紹了四種常用的時序預測方法及其在 Python 中的實現，希望這些示例能幫助你更好地理解和應用時序預測技術。如果有任何其他問題或需要進一步的解釋，請隨時提問。
責任編輯：華軒
來源：
測試開發學習交流
