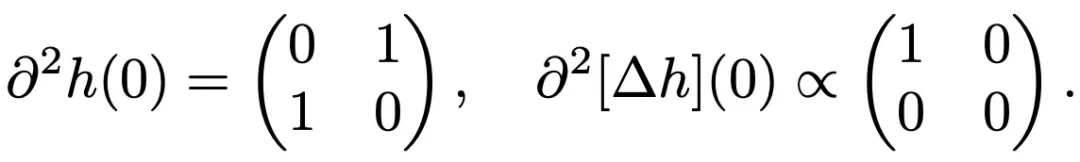擴散模型、最優傳輸存在什么關系?法國數學家4頁論文引網友圍觀
擴散模型和最優傳輸之間到底存在怎樣的聯系?對很多人來說還是一個未解之謎。
但有一點很清楚的是:在相似的數據集上訓練的不同擴散模型傾向于恢復出相似的映射關系。
這就提出一個問題:如果這些映射關系不是最優傳輸(OT,Optimal Transport )映射,那么它們到底在什么意義上是最優呢?
2022 年,博科尼大學助理教授 Hugo Lavenant 與里昂第一大學教授 Filippo Santambrogio 合作,在論文《 THE FLOW MAP OF THE FOKKER-PLANCK EQUATION DOES NOT PROVIDE OPTIMAL TRANSPORT 》中探討了流模型在最優傳輸框架中的應用,并提供了一個反例,表明在某些情況下,流模型并不能實現最優傳輸。

論文地址:https://cvgmt.sns.it/media/doc/paper/5469/counterexample_flow_v3.pdf
在這篇文章的摘要部分,作者表示,Khrulkov 和 Oseledets 在先前研究中(論文:Understanding DDPM Latent Codes Through Optimal Transport)提出了一個猜想,該猜想認為通過積分 Fokker-Planck 方程的 Wasserstein 速度得到的 ODE 流,可以獲得一個最優傳輸映射。
然而,在 Kim 和 Milman 的論文中《A generalization of Caffarelli’s contraction theorem via (reverse) heat flow》,這一結果被認為是錯誤的,但沒有提供證明。Hugo Lavenant、Filippo Santambrogio 的這篇論文正好展示了 Khrulkov 和 Oseledets 所聲稱的結果不能成立。
但這篇文章過于晦澀難懂,全篇論文看下來幾乎都是推導公式且篇幅又長。
為此,法國數學家 Gabriel Peyré 在論文《 Diffusion models and Optimal Transport 》中給出了一個很好的概括,文章重述了 Hugo Lavenant 和 Filippo Santambrogio 關于簡潔證明的主要內容,即一般情況下,擴散模型不能定義最優傳輸映射。
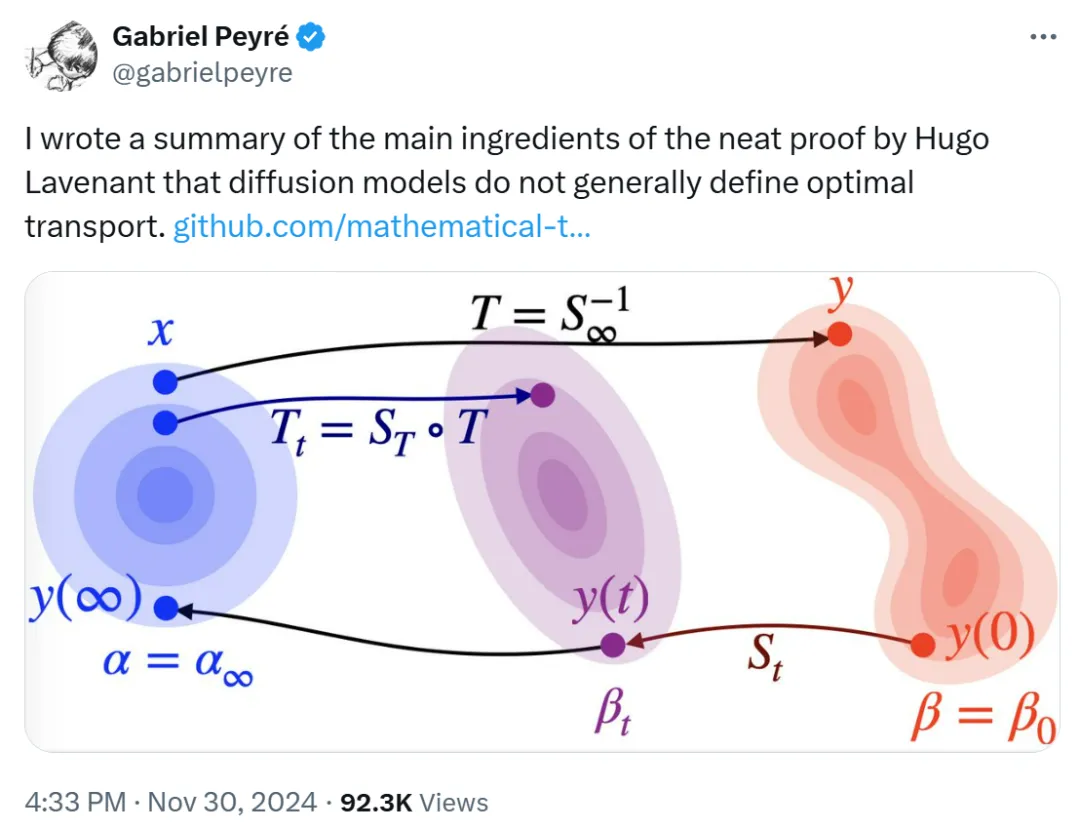

地址:https://github.com/mathematical-tours/mathematical-tours.github.io/blob/971ddb3aab5803c7a4abef122f878292f6a6c25d/book-sources/diffusion-models/note-diffusion-ot.pdf
接下來,我們看看這篇文章講了什么內容。
生成模型旨在在參考分布 α(通常是各向同性高斯分布)和數據分布 β 之間構建傳輸映射 T。用 T?α 表示 α 被 T 向前推進(如果 α 是由 Dirac 質量在 x_i 處構成的,那么 T?α 是由 Dirac 質量在 T(x_i)處構成的)。
因此,目標是找到 T,使得 T?α = β 。很明顯,對于任何 β,這樣的映射總是存在的,但找到 T 的明確構造方法卻出奇地困難。
這里有兩種標準方法,分別是最優傳輸和集成擴散過程的逆向積分伴隨的平流場。
最優傳輸
最優傳輸通過求解 Monge 問題求出 T:
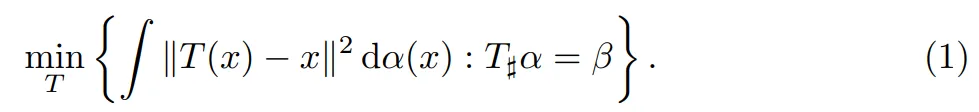
1991 年,Brenier 著名定理表明這個映射是存在的,且是唯一的,并且可以寫成一個凸函數 T =?φ 的梯度。根據質量守恒定律,即 T?α = β ,等價于說 φ 解決了 Monge-Ampère 方程:
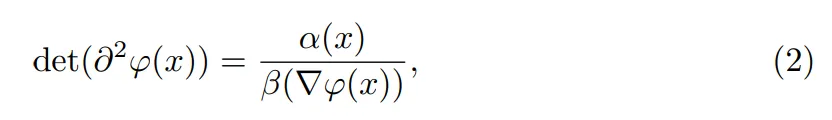
逆向 Flow Map
擴散模型需要考慮 β_0 = β 和 β_∞= α =N (0,Id) 之間的差值 β_t ,求解過程定義如下:
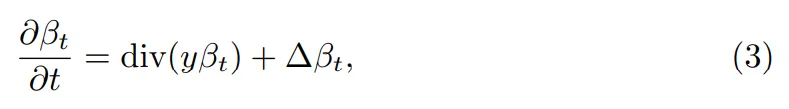
請注意,使用 y 來表示空間變量,因為演化是逆向進行的,即從數據 β 到后一個變量 α,它收斂于 β_∞= α。
將方程寫成離散形式:
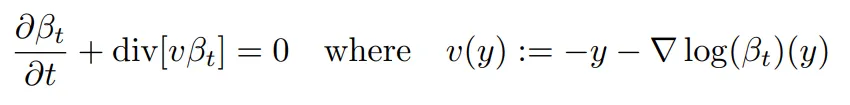
這表明,如果已經計算出了 β_t,那么這種演化可以根據向量場 v 演化粒子來獲得。

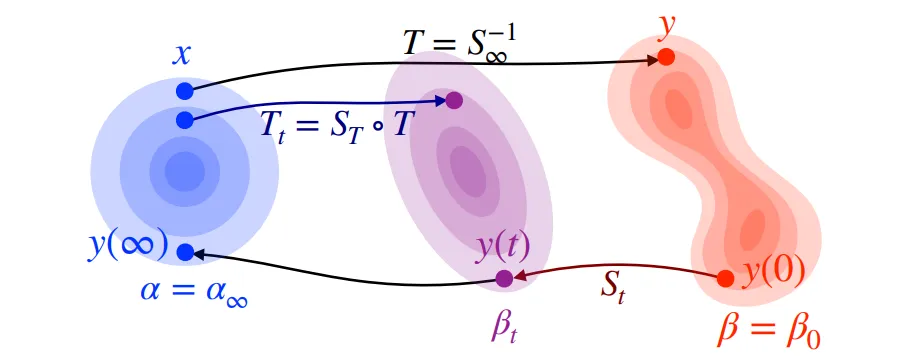
映射 S_t 就是 flow map :
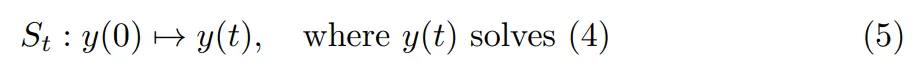
逆向 Flow Map 不是最優傳輸
人們很自然地想知道逆向 Flow Map 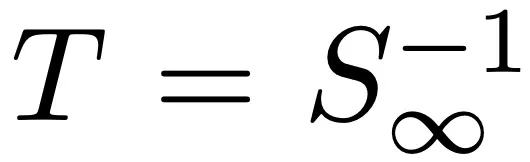 是否是 (1) 的解。在一維情況下,S_t 定義微分同胚( diffeomorphism),因此
是否是 (1) 的解。在一維情況下,S_t 定義微分同胚( diffeomorphism),因此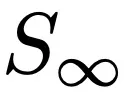 是單調的,
是單調的,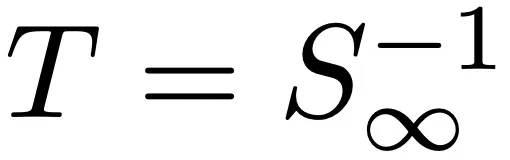 也是單調的。因此,它是凸函數的梯度,根據 Brenier 定理使其最優。如果 β 是高斯分布,直到空間旋轉以使協方差對角化,則擴散映射由沿每個軸的單調映射定義,并且也是最優傳輸。
也是單調的。因此,它是凸函數的梯度,根據 Brenier 定理使其最優。如果 β 是高斯分布,直到空間旋轉以使協方差對角化,則擴散映射由沿每個軸的單調映射定義,并且也是最優傳輸。
Lavenant 和 Santambrogio 通過矛盾證明,一般來說,逆向 flow map 并不是最優傳輸。他們構造了一個接近各向同性高斯 α 的 β,但他們沒有證明 β 的猜想是錯誤的,而是證明存在一些 t ≥ 0,使得從 α 到 β_t 的逆向 Flow Map T_t 不是最優傳輸。他們實際上表明,對于某些 t_0 > 0,T_t 并不是所有 t ∈ (0, t_0] 的最優傳輸。
用 S_t 表示從 β_0 = β 到 β_t 的 Flow Map。如果猜想成立,則從 α 到 β_t 的逆向 Flow Map T_t 是所有 t 的最優傳輸。根據 Flow Map 的構成規則,該 Map 為:

并且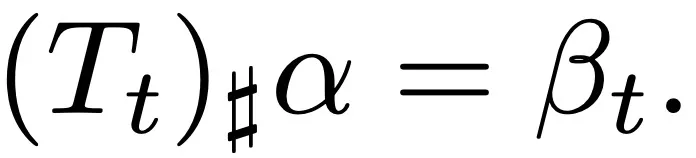 目標是證明:如果 β 選擇得當(具體來說,非常接近 α,且特定的二階和四階對數密度導數為 0),那么 T_t 是所有 t 的最優傳輸會導致矛盾。根據 Brenier 定理,T_t 是最優傳輸意味著它是凸函數的梯度,這相當于:
目標是證明:如果 β 選擇得當(具體來說,非常接近 α,且特定的二階和四階對數密度導數為 0),那么 T_t 是所有 t 的最優傳輸會導致矛盾。根據 Brenier 定理,T_t 是最優傳輸意味著它是凸函數的梯度,這相當于:
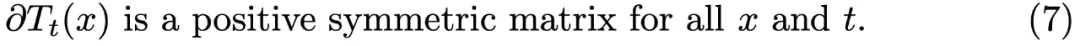
結合:
- 對 (7) 對 t 求微分
- 對流 ODE (4) 對 x 求微分
然后在 t = 0 時評估所獲得的方程,Hugo 和 Filippo 通過顯式計算表明,這會導致:
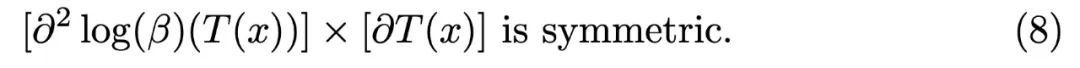
利用基本性質:A、B 對稱且 AB 對稱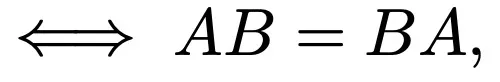 則 (8) 意味著:
則 (8) 意味著:
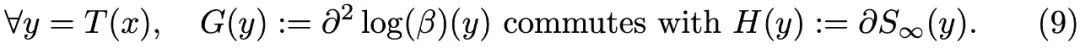
為了達到矛盾,假設 G (y) 和 H (y) 對于所有 y 都是可交換的。由于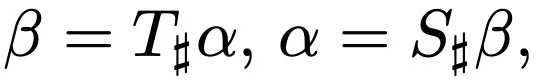 并且 T 和 S 是逆最優傳輸映射,因此將
并且 T 和 S 是逆最優傳輸映射,因此將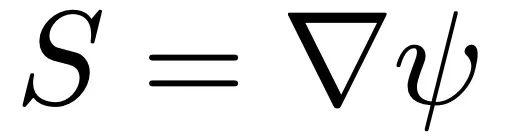 表示為 ψ 凸。Monge-Amp`ere 方程 (2) 意味著:
表示為 ψ 凸。Monge-Amp`ere 方程 (2) 意味著:
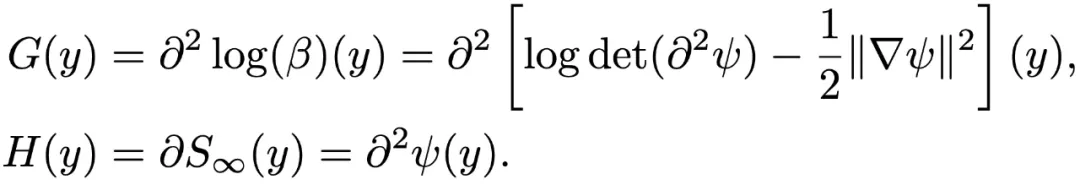
為了使 β 接近 α,請考慮:對于較小的 ε,
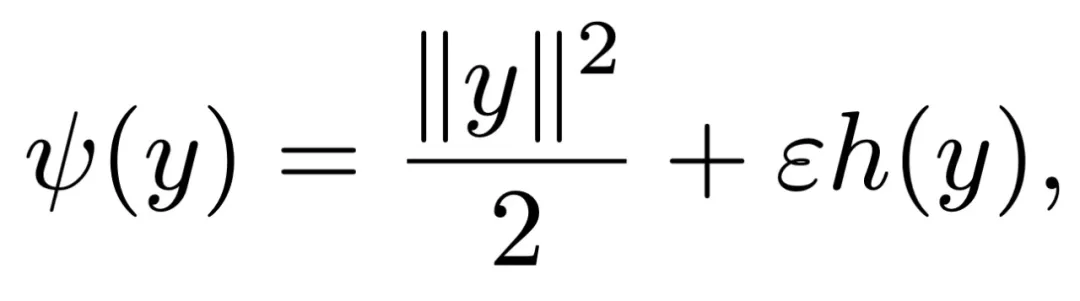
在泰勒級數中展開,經過一些計算:
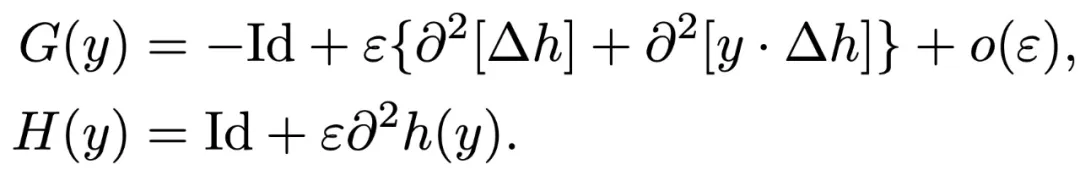
著眼于 y = 0,目標是通過設計 h 來達到矛盾,使得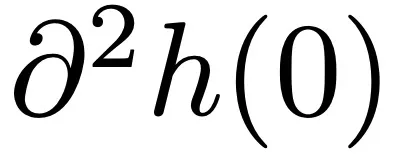 和
和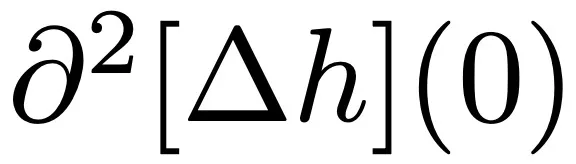 不能交換。在 0 附近,h 必須至少是 4 次多項式。二維情況下的一個示例是:
不能交換。在 0 附近,h 必須至少是 4 次多項式。二維情況下的一個示例是:
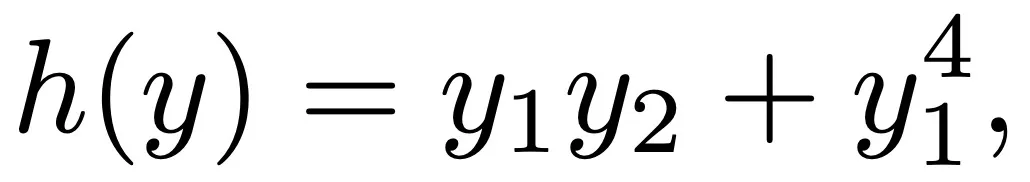
產生: