機器學習中分類任務的常用評估指標和Python代碼實現
假設您的任務是訓練ML模型,以將數據點分類為一定數量的預定義類。 一旦完成分類模型的構建,下一個任務就是評估其性能。 有許多指標可以幫助您根據用例進行操作。 在此文章中,我們將嘗試回答諸如何時使用? 它是什么? 以及如何實施?
混淆矩陣
混淆矩陣定義為(類x類)大小的矩陣,因此對于二進制分類,它是2x2,對于3類問題,它是3x3,依此類推。 為簡單起見,讓我們考慮二元分類并了解矩陣的組成部分。
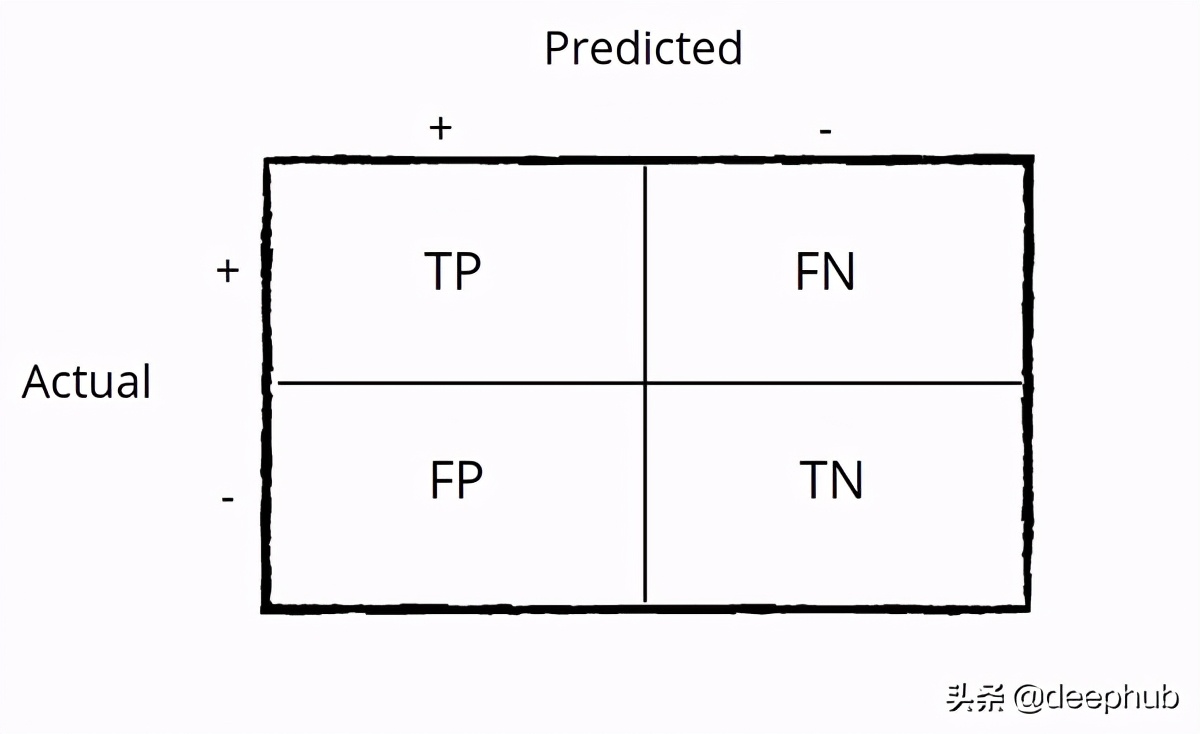
真實正值(TP)-表示該類為“真值”的次數,您的模型也表示它為“真值”。 真負數(TN)-表示該類為假值的次數,您的模型也表示它為假值。 誤報(FP)-表示該類為假值,但您的模型表示為真值。
您可以通過這種方式記住它—您的模型錯誤地認為它是肯定的
假陰性(FN)-表示該類為“真值”的次數,但您的模型表示為“假值”。
您可以通過這種方式記住它-您的模型錯誤地認為它是假值的
您可以使用sklearn輕松獲得混淆矩陣,如下所示-
- from sklearn import metricsdef calculate_confusion_matrix(y, y_pred):
- return metrics.confusion_matrix(y, y_pred)
如圖1所示,混淆矩陣的成分是TP,TN,FP,FN,您也可以使用普通python計算它們,如下所示- 計算TP,TN,FP,FN
- def calculate_TP(y, y_pred):
- tp = 0
- for i, j in zip(y, y_pred):
- if i == j == 1:
- tp += 1
- return tp
- def calculate_TN(y, y_pred):
- tn = 0
- for i, j in zip(y, y_pred):
- if i == j == 0:
- tn += 1
- return tn
- def calculate_FP(y, y_pred):
- fp = 0
- for i, j in zip(y, y_pred):
- if i == 0 and j == 1:
- fp += 1
- return fp
- def calculate_FN(y, y_pred):
- fn = 0
- for i, j in zip(y, y_pred):
- if i == 1 and j == 0:
- fn += 1
- return fn
混淆矩陣對于理解模型的細粒度性能很重要,然后根據用例的敏感性,可以確定此模型是否良好。 例如,在醫學診斷用例中,您希望模型的假陰性率非常低,因為您不希望系統在測試該人的任何疾病的蹤跡時如果事實為“是”,則說“否”。 您仍然可以設法使誤報率偏高,因為此人可以通過相關測試并在以后的階段得到確認。
準確率 Accuracy
準確使人們對模型的運行方式有了整體認識。 但是,如果使用不正確,它很容易高估這些數字。 例如-如果類標簽的分布偏斜,則僅預測多數類會給您帶來高分(高估性能),而對于平衡類而言,準確性更有意義。
您可以使用sklearn輕松獲得準確性得分,如下所示-
- from sklearn import metrics
- def calculate_accuracy_sklearn(y, y_pred):
- return metrics.accuracy_score(y, y_pred)
也可以使用Python從混淆矩陣組件中計算出來,如下所示-
- def calculate_accuracy(y, y_pred):
- tp = calculate_TP(y, y_pred)
- tn = calculate_TN(y, y_pred)
- fp = calculate_FP(y, y_pred)
- fn = calculate_FN(y, y_pred)
- return (tp+tn) / (tp+tn+fp+fn)
精度 Precision
精度度量有助于我們理解識別陽性樣本的正確性%。例如,我們的模型假設有80次是正的,我們精確地計算這80次中有多少次模型是正確的。
也可以計算如下-
- def calculate_precision(y, y_pred):
- tp = calculate_TP(y, y_pred)
- fp = calculate_FP(y, y_pred)
- return tp / (tp + fp)
召回率 Recall
召回指標可幫助我們了解模型能夠正確識別的所有地面真實正樣本中正樣本的百分比。 例如-假設數據中有100個陽性樣本,我們計算出該100個樣本中有多少個模型能夠正確捕獲。
也可以如下所示進行計算-
- def calculate_recall(y, y_pred):
- tp = calculate_TP(y, y_pred)
- fn = calculate_FN(y, y_pred)
- return tp / (tp + fn)
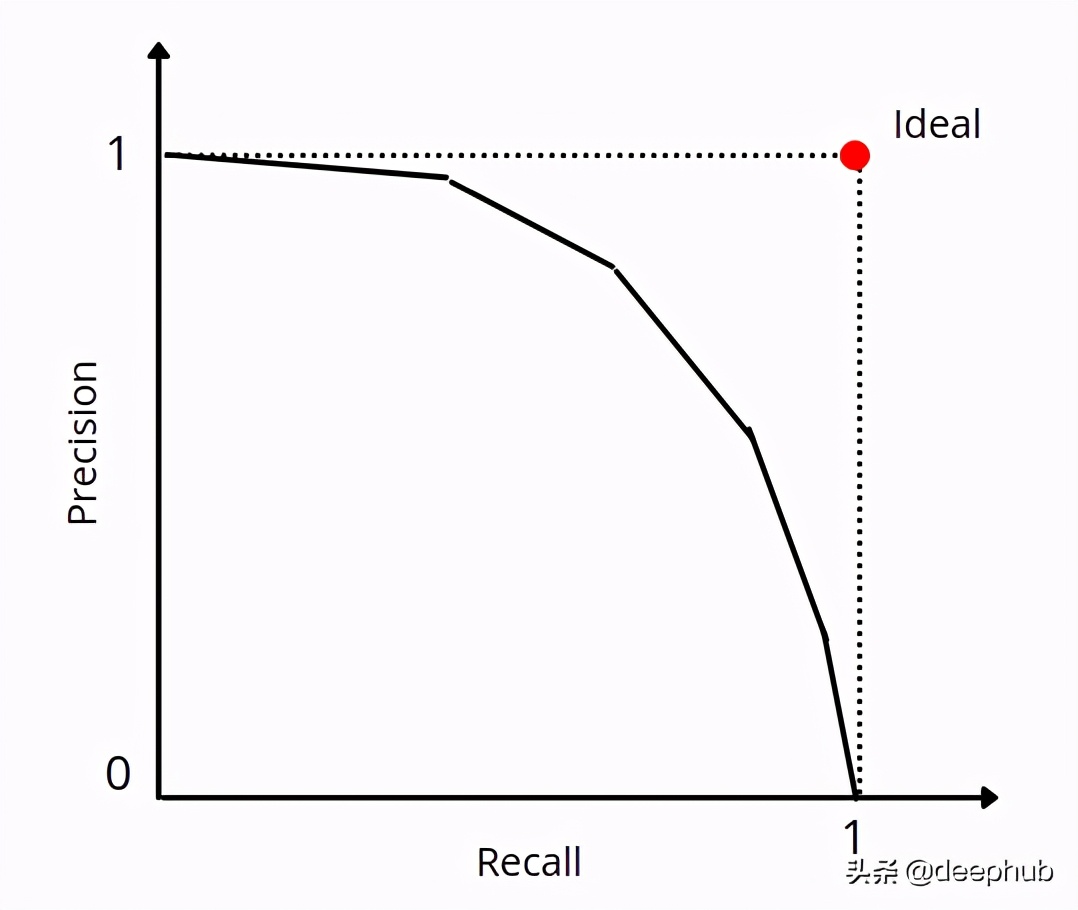
對于那些將概率作為輸出的模型,調整閾值然后填充相關的混淆矩陣和其他屬性始終是一個好習慣。 可以繪制不同閾值的精確召回曲線,并根據用例的敏感性選擇閾值。
- def precision_recall_curve(y, y_pred):
- y_pred_class,precision,recall = [],[],[]
- thresholds = [0.1, 0.2, 0.3, 0.6, 0.65]
- for thresh in thresholds:
- for i in y_pred: #y_pred holds prob value for class 1
- if i>=thresh: y_pred_class.append(1)
- else: y_pred_class.append(0)
- precision.append(calculate_precision(y, y_pred_class))
- recall.append(calculate_recall(y, y_pred_class))
- return recall, precisionplt.plot(recall, precision)
F1分數
F1結合了Precision和Recall得分,得到一個單一的數字,可以幫助直接比較不同的模型。 可以將其視為P和R的諧波均值。諧波均值是因為與其他方式不同,它對非常大的值不敏感。 當處理目標傾斜的數據集時,我們通常考慮使用F1而不是準確性。
您可以如下所示進行計算-
- def calculate_F1(y, y_pred):
- p = calculate_precision(y, y_pred)
- r = calculate_recall(y, y_pred)
- return 2*p*r / (p+r)
AUC-ROC
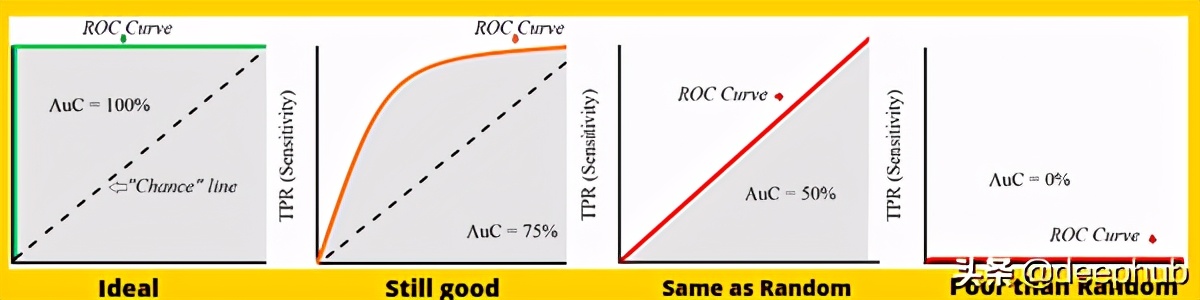
AUC-ROC是用于二分類問題的非常常見的評估指標之一。 這是一條曲線,繪制在y軸的TPR(正確率)和x軸的FPR(錯誤率)之間,其中TPR和FPR定義為-

如果您注意到,TPR和Recall具有相同的表示形式,就像您正確分類了多少正確樣本一樣。 另一方面,FPR是被錯誤分類的負面示例的比例。 ROC圖總結了每個閾值的分類器性能。 因此,對于每個閾值,我們都有TPR和FPR的新混淆矩陣值,這些值最終成為ROC 2-D空間中的點。 ROC曲線下的AUC(曲線下的面積)值越接近1,模型越好。 這意味著一般而言,對于具有較高AUC的每個閾值,我們的模型都比其他模型具有更好的性能。
您可以如下所示進行計算-
- from sklearn.metrics import roc_auc_score
- def roc_auc(y, y_pred):
- return roc_auc_score(y, y_pred)
Precision @ k
Precision @ k是用于多標簽分類設置的流行指標之一。 在此之下,我們計算給定示例的前k個預測,然后計算出這k個預測中有多少個實際上是真實標簽。 我們將Precision @ k計算為-
Precision@k = (# of correct predictions from k) / (# of items in k)
- actual_label = [1, 1, 0, 0, 1]
- predicted_label = [1, 1, 1, 0, 0]
- Let k=3
- Precision@k = 2/3 (It's same as TP/(TP+FP))
log損失
當您遇到二分類問題時,log損失是相當不錯的。 當您有一個模型輸出概率時,該模型將使用該模型,該模型會根據預測與實際標簽的偏差來考慮預測的不確定性。
您可以如下所示進行計算-
- def calculate_log_loss(y, y_pred_probs):
- log_loss = -1.0*(t*log(p) + (1-t)*(t*log(1-p))
- return log_loss
在不平衡數據集的情況下,您還可以添加類權重來懲罰少數類相對于多數類的錯誤。在代碼中,w1和w2分別對應正類和負類的權重。
- def calculate_log_loss_weighted(y, y_pred):
- log_loss = -1.0*(w1*t*log(p) + w2*(1-t)*(t*log(1-p))
- return log_loss
附注:您可以很容易地將其擴展到稱為交叉熵的多類設置。
Brier分數
當任務本質上是二元分類時,通常使用Brier分數。 它只是實際值和預測值之間的平方差。 對于N組樣本,我們將其取平均值。
您可以如下所示進行計算-
- def brier_score(y, y_pred):
- s=0
- for i, j in zip(y, y_pred):
- s += (j-i)**2
- return s * (1/len(y))
在本篇文章中,我們看到了一些流行的評估指標,每個數據科學家在根據手頭問題的性質評估機器學習分類模型時都必須牢記這些評估指標。