LLMs并非智能思考者:引入數學主題樹基準來全面評估LLMs 原創 精華
摘要:大型語言模型(LLMs)在數學推理方面展示了令人印象深刻的能力。然而,盡管取得了這些成就,當前的評估主要限于特定的數學主題,尚不清楚LLMs是否真正參與了推理。為了解決這些問題,我們提出了數學主題樹(MaTT)基準,一個具有挑戰性和結構化的基準,涵蓋了廣泛的數學科目,提供了1958個問題,每個問題都配有詳細的分層主題鏈。在使用MaTT基準評估不同的LLMs后,我們發現最先進的模型GPT-4在多項選擇題中僅取得了54%的準確率。有趣的是,即使使用“思維鏈提示”方法,我們也觀察到幾乎沒有顯著的改進。此外,當問題不提供選擇時,LLMs的準確率顯著下降,最高減少了24.2個百分點。對LLMs在各個主題上的表現進行詳細分析后發現,即使在同一一般數學領域內,密切相關的子主題之間也存在顯著差異。為了找出LLMs表現背后的原因,我們對在提供選擇時由GPT-4生成的解釋的完整性和正確性進行了人工評估。令人驚訝的是,我們發現僅在53.3%的情況下,模型提供的正確答案的解釋被認為是完整和準確的,即模型真正進行了推理。
1.引言
大型語言模型(LLMs)在數學推理方面表現出令人矚目的能力,凸顯了它們在復雜問題解決領域的潛力(Chowdhery et al., 2022;Touvron et al., 2023;OpenAI, 2023;Team et al., 2023)。最近的研究表明,LLMs在應用于數學問題時,可以展示出高度的推理能力,往往在某些情況下與人類水平相當甚至超越人類。這種數學推理能力通過一些創新技術如思維鏈(Wei et al., 2022)、思維樹(Yao et al., 2024)和自我驗證(Weng et al., 2022)得到了進一步增強,強調了在解決數學問題過程中程序步驟的重要性。
盡管有這些進步,我們對LLMs數學推理能力的理解仍存在幾個關鍵的空白。首先,尚不清楚LLMs在哪些特定的數學領域表現出色或不足,因為缺乏跨多樣數學領域的全面評估。其次,區分LLMs依賴記憶與真正推理的實例具有挑戰性,令人質疑它們理解的深度。第三,對多項選擇格式對LLMs行為的影響尚未充分了解,這表明模型的表現可能受到所提出問題結構的影響。這些空白強調了需要一個更為健全的基準,能夠全面評估LLMs,幫助我們解析它們的優點、缺點及其解決問題策略的細微差別。
在本文中,我們通過最初利用維基百科的“數學主題列表”2識別數學中的關鍵領域,開發了數學主題樹(MaTT)基準,涵蓋了純數學和應用數學的十二個主要主題。接著從維基百科提取每個主題的重要參考書籍,構建詳細的主題樹。然后,我們使用這些書籍的目錄進一步完善基準,構建反映數學知識層次結構的綜合樹。在完成主題樹后,我們從這些書籍的子章節中提取問題,并將它們收集在葉節點下。最后,我們為每個問題配上多項選擇選項,增強了基準在評估數學理解方面的實用性。圖1展示了MaTT的示意圖。
開發MaTT后,我們評估了各種LLMs的數學推理能力,包括商業模型如GPT-4(OpenAI, 2023)和ChatGPT(Kocón et al., 2023)(turbo版本),以及開源的LLM,Mistral(Jiang et al., 2023)。值得注意的是,在多項選擇格式中,最先進的GPT-4僅取得了54%的準確率。此外,使用思維鏈提示并未顯著提高LLMs的表現,這強調了基準的復雜性,并表明單純的逐步推理可能不足。當問題不提供多項選擇選項時,我們觀察到LLMs的準確率顯著下降,最高下降了24.2個百分點。此外,我們對LLMs在不同主題上的表現進行了全面分析,發現存在顯著差異,突顯了模型在解決同一數學領域內相關子主題時能力的不一致性。
為了理解LLMs表現不足及其在不同主題上結果不一致的根本原因,我們對GPT-4提供的解釋進行了詳細評估。令人驚訝的是,在模型回答正確的情況下,只有53.3%的解釋被認為是完整的,即GPT-4進行了真正的推理。這些情況通常與較簡單或更為人熟知的問題相關,這些問題只需要一些簡單的步驟即可解決。對于需要更多步驟、復雜計算或創造性/智能解決問題的更復雜問題,LLMs往往失敗或依賴于替代策略。這些策略包括選擇工程、不支持的定理使用、循環推理或盲目記憶,而非真正的數學推理。
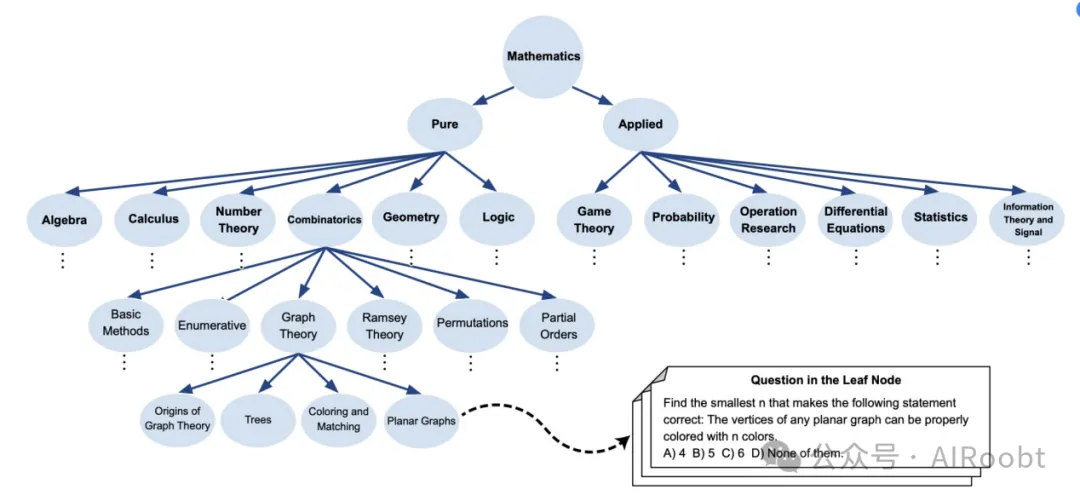
圖 1:數學主題樹 (MaTT) 基準的概述,這是一項具有挑戰性且結構化的基準,提出了涵蓋各種數學科目問題的基準,每個科目都與詳細的層次結構主題相關。
2.MaTT:數學主題樹基準
近年來,大型語言模型(LLMs)在數學推理方面展示了顯著的能力。然而,由于當前基準測試通常集中在特定的數學領域,其能力尚未完全理解。這種局限性阻礙了我們對LLMs推理能力深度和廣度的理解。迫切需要更全面的數學基準測試,涵蓋更廣泛的主題,并深入了解模型的推理過程。這類基準不僅可以在更廣泛的數學范圍內挑戰模型,還可以幫助更好地理解這些模型如何以及在何處應用推理。
為了解決這一差距,本文創建了數學主題樹(MaTT)基準。為了創建MaTT,我們首先利用維基百科上的“數學主題列表”作為基礎資源。這一探索對于確定我們要涵蓋的數學知識范圍至關重要。從維基百科提取數學主題列表后,我們確定了十二個主要主題,這些主題全面涵蓋了純數學和應用數學的廣度。然后,我們從相應的維基百科頁面上提取了每個主題的一個或多個關鍵參考書籍。這些主題及其對應的資源如下:純數學包括代數(Meyer, 2023;Herstein, 1991;McGee, 2002)、微積分與分析(Stewart, 2012)、數論(Niven et al., 1991)、組合數學(Bóna, 2002)、幾何與拓撲(Coxeter, 1969;Coxeter and Greitzer, 1967;Engelking, 1989)和邏輯(Mendelson, 2009)。應用數學包括博弈論(Osborne and Rubinstein, 1994)、概率(Tijms, 2012, 2017)、運籌學(Hillier and Lieberman, 2015)、微分方程(Boyce et al., 2021)、統計學(Hogg et al., 2013)以及信息理論與信號處理(Cover, 1999;Proakis, 2007)。
接下來,我們利用這些選定參考書籍的目錄來豐富和構建MaTT主題樹。這種方法使我們能夠按照這些書籍中呈現的主題和子主題的層次結構進行映射,從而創建一個反映數學領域深度和互聯性的綜合圖。創建MaTT的最后一步是從參考書籍的各章節中詳細提取問題,并將它們收集在主題樹的葉節點下。對于每個識別出的問題,我們設計了多項選擇選項,以便于客觀評估框架的建立。為了生成這些選項,我們選擇了與實際答案非常接近的選擇,如具有相似數值的選項、通過省略證明中的某一步得到的選項,或提供替代組合的選項。例如,如果正確答案是“A & B”,我們會將“A or B”作為可能的選擇之一。圖1展示了MaTT的示意圖。
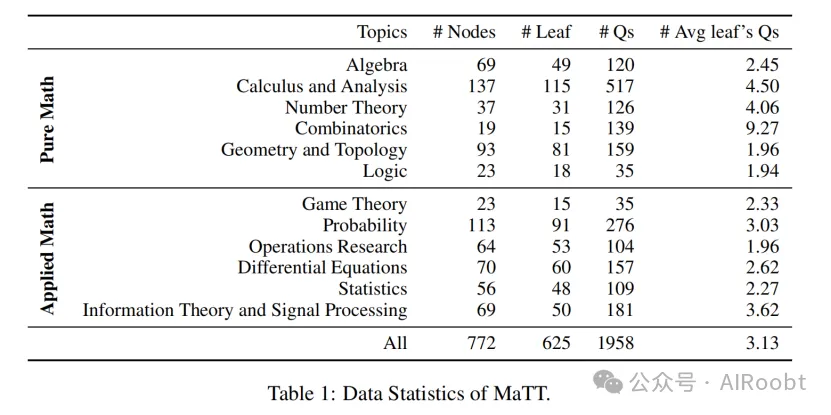
MaTT基準的統計概述詳見表1。該基準包含1958個示例,精心策劃于12個不同的數學主題,涵蓋了純數學和應用數學的廣度。在匯集這些問題時,我們旨在確保所有主題具有廣泛而一致的難度范圍。在提取問題時,我們排除了過于流行或簡單的問題,以減少數據污染的風險。
3.實驗細節
我們使用MaTT基準評估了商業LLMs——GPT-4(OpenAI, 2023)和ChatGPT(Kocón et al., 2023)(turbo版本),以及開源LLM,Mistral(Jiang et al., 2023)(Mistral-7B-Instruct-v0.2)的性能。在我們的評估中,我們將提示結構化為要求LLMs首先生成解釋,然后再給出最終答案。在多項選擇設置中,我們特別指示模型選擇提供的選項(A、B、C或D)作為最終答案。此外,對于零樣本思維鏈提示,我們在提示中附加了“讓我們一步一步地思考”。實驗中使用的提示示例在附錄中提供。
4.實驗
在本節中,我們首先使用MaTT基準分析LLMs的數學推理能力。隨后,我們考察模型在不同子主題上的表現差異。接著,我們通過不提供多項選擇選項來評估選擇可用性對LLMs的影響。最后,我們重點分析GPT-4的解釋,手動注釋每個解釋中的推理水平,并探索GPT-4用來得出正確答案的策略。
4.1 LLMs在MaTT上的表現
表2展示了LLMs在MaTT基準上各個主題的準確率。所有模型的表現都明顯較低,GPT-4僅達到約54%的準確率,而Mistral的表現接近隨機選擇。詳細檢查發現,Mistral經常拒絕回答,聲稱正確選項不在提供的選項中,而其他模型則嘗試選擇最接近的匹配項,或者在計算的答案不在列表中時,進行某種形式的推理。
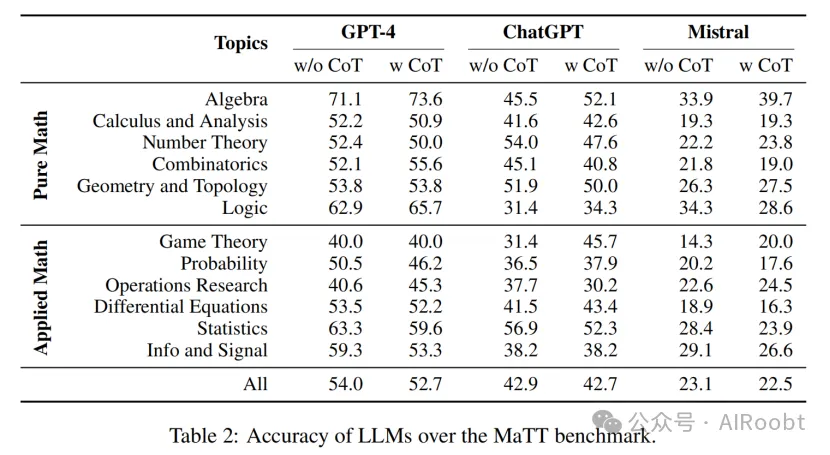
此外,LLMs在不同主題上的準確率差異顯著,差距高達31%,這突顯了LLMs在理解和推理能力方面的顯著差異。最后,我們觀察到零樣本思維鏈提示大多未能提升模型性能,可能是由于問題的復雜性。MaTT中的許多問題需要復雜或大量的步驟,或需要智能/創造性的思維,僅僅按照幾個簡單步驟無法解決。這一觀察結果對思維鏈提示在許多推理任務中的有效性假設提出了質疑。許多現有的推理任務評估基準設計為通過幾個簡單步驟即可解決(Srivastava et al., 2022),而現實世界的推理通常涉及多個步驟并需要創造性的問題解決。
4.2 LLMs表現的按主題細分
如上一節所述,對LLMs在各種主題或同一數學領域內不同子主題上的數學推理能力的探索仍然顯著不足。圖2和圖3分別詳細展示了LLMs在MaTT基準中純數學和應用數學子主題上的準確率。
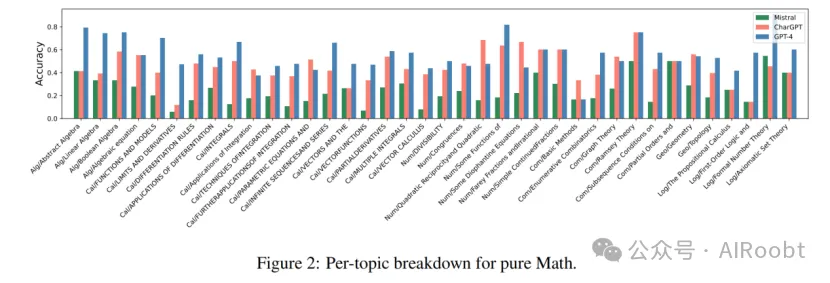
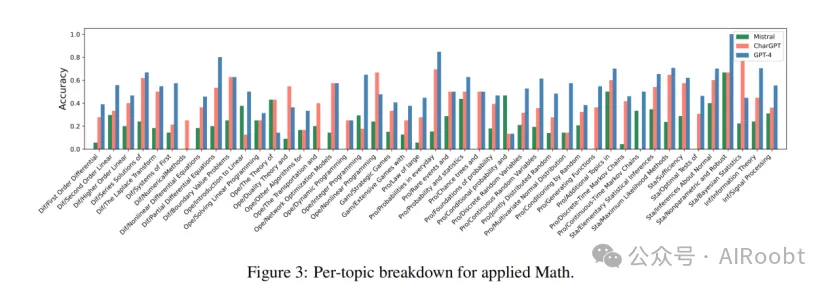
這些圖表明,模型即使在同一主要主題的子主題內也表現出不同程度的準確率,強調了它們在理解和推理能力方面的差異,即使在密切相關的學科中也是如此。值得注意的是,我們發現,在某些子主題上,如積分的應用、參數方程、二次互反、丟番圖方程、對偶理論、非線性規劃、條件概率、連續時間馬爾可夫鏈和基礎統計學,ChatGPT和Mistral的表現優于GPT-4。這一觀察結果進一步強調了不僅要超越高層次主題的整體表現,還要在更細粒度的水平上考察模型的表現,以全面理解它們的數學推理能力。
4.3 LLMs在無選項情況下的表現
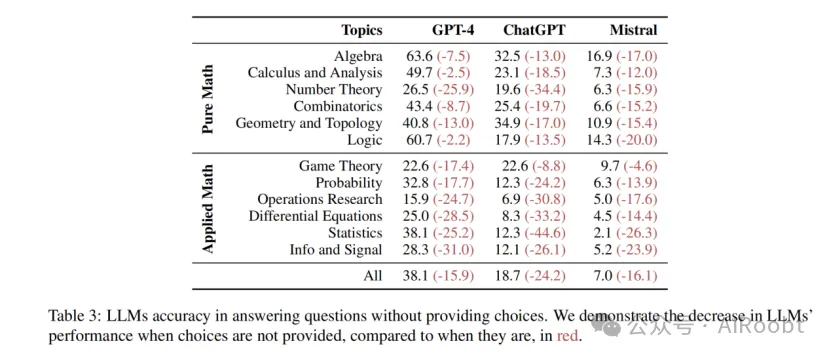
為了更深入地探討LLMs的數學推理能力,我們評估了它們在沒有多項選擇選項幫助下的MaTT基準表現。我們手動評估了在沒有選項情況下,模型在MaTT上的準確率,并將結果列于表3中。結果顯示,性能大幅下降,其中GPT-4、ChatGPT和Mistral分別損失了29.4%、56.4%和69.7%的準確率。這一顯著下降突顯了模型在推導答案時對選項的依賴性,顯示了它們在真正數學推理方面的局限性。這也強調了不能僅依賴單一的總體評分來評估LLMs推理能力的重要性。我們在第4.5節中提供了對選擇可用性對LLMs預測影響的更詳細分析。
4.4 解釋的推理水平
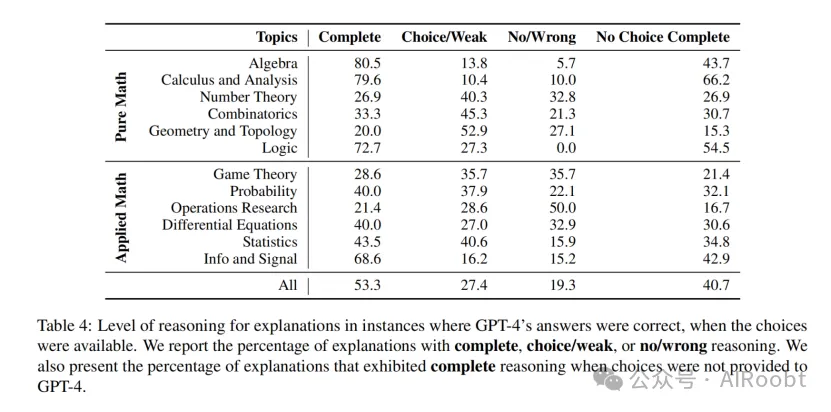
為了理解LLMs在無選項情況下表現不佳及其在不同主題上準確率變化的原因,我們對LLMs為其預測生成的解釋的完整性和準確性進行了手動檢查。鑒于GPT-4相對于其他評估的LLMs表現較好,本節的分析特別集中在GPT-4生成的解釋上。我們的目標是確定在正確預測的實例中(有選項時),解釋屬于以下類別的百分比:(1)完整推理,解釋詳盡且邏輯合理;(2)選項/弱推理,模型利用給定選項或提供部分推理的策略;(3)無/錯誤推理,解釋錯誤或缺失,模型在沒有理由的情況下得出結論。此外,我們計算了在所有GPT-4正確回答(有選項)的情況下,GPT-4在無選項時仍提供正確答案并給出完整解釋的實例百分比。
我們對GPT-4在有選項時預測正確的樣本的解釋進行了手動評估,結果詳見表4。值得注意的是,我們發現僅53.3%的正確回答問題的解釋是完整的,即GPT-4進行了實際推理,這突顯了GPT-4在實際推理能力上的顯著不一致性。此外,我們觀察到不同主題上的解釋完整性水平不一,并不一定與GPT-4在這些主題上的總體表現相關。當比較有無選項情況下完整解釋的樣本時,我們注意到一個顯著差距,這表明選項的存在有助于模型更好地導航或回憶推理過程。此外,我們注意到GPT-4主要在解決較簡單或更為人熟知的問題時真正進行了推理,這些問題通過幾個簡單步驟即可解決,而在需要更多復雜步驟或創造性問題解決的情況下,GPT-4經常失敗或依賴于不同的策略(我們在第4.5節中更詳細地探討這些策略)。這與思維鏈提示在提升LLMs性能上的有限有效性觀察結果一致。我們在附錄中提供了更多關于解釋的分析。
4.5 從解釋中觀察到的現象
除了注釋解釋的推理水平(如表4所示),我們還指出了GPT-4在不涉及推理時得出正確答案所采用的策略。我們總結了以下策略:
選項工程 指的是模型(如GPT-4)操縱或利用可用的多項選擇選項來確定答案,而不是依賴于深刻理解或真正的推理過程。這可以分為以下幾種情況:
- 使用選項:在這種情況下,GPT-4直接使用選項并選擇最符合問題的一個。例如,在線性規劃問題中,盡管沒有選項時GPT-4無法回答任何優化問題,但在有選項時,通過這種策略,GPT-4通過簡單選擇選項中的最小或最大值,取得了很高的表現。
- 推導出一個合理的答案:在這種策略中,GPT-4通過排除不合理的選項來選擇答案,而不是實際推理。例如,生成具有參數α和β的貝塔分布的X時,GPT-4通過排除不合理選項并提供類似的論據,正確得出了答案,但沒有進行任何實際推理。
- 選項專家:GPT-4似乎了解選項通常是如何設置的。例如,在計算事件X和Y的概率時,GPT-4僅能得出事件X的概率為1/3,然后在沒有任何推理的情況下,聲稱事件Y的概率不能為1/3,然后選擇選項A,盡管還有“以上都不是”這個選項。
- 中間地帶規則:我們觀察到GPT-4傾向于在無法找到正確答案時選擇中間值。例如,在計算游戲預期持續時間的問題中,GPT-4選擇了中間值作為最合理的選項。
定理使用 指的是模型(如GPT-4)利用一個定理或性質,這實際上是問題的主要挑戰部分。通過直接應用它,繞過復雜的推導而達到解決方案。例如,在求范德蒙矩陣行列式的問題中,GPT-4直接給出了定理的結果,而沒有解釋或證明。
循環推理 是一種邏輯謬誤,其中論證的結論作為前提來支持自身。這種策略與幻覺密切相關,且非常難以檢測。在這些情況下,推理從同一點開始和結束,論證本質上是說“A是正確的,因為B是正確的,而B是正確的因為A是正確的”。
盲記憶 我們指的是LLMs有時傾向于盲目記住問題的答案,而不學習其必要步驟或背后的推理。例如,在計算單位正方形、單位圓和邊長為單位的等邊三角形內隨機選擇的兩點之間的期望距離時,GPT-4直接給出了已知的答案,而沒有進行任何詳細的計算。這些例子說明了盲記憶如何使LLMs在推理和回答相似問題時無能為力。
5.相關工作
隨著LLMs的不斷增強,它們在現有基準測試中的數學推理能力也顯著提升。然而,目前的評估范圍在涵蓋的數學領域廣度上仍有限,無法最終確定這些模型是否真正參與了推理,還是依賴于替代策略來找到答案。
數學基準測試
先前的研究主要集中在為數學文字題(以書面描述形式呈現的數學問題)開發基準測試——這些問題通常只需要幾個步驟來解決,通常涉及基本算術或初等代數(Ling et al., 2017;Cobbe et al., 2021;Patel et al., 2021)。此外,Mishra等人(2022)的工作引入了一個全面的數學推理基準,涵蓋了四個維度的23項不同任務:數學能力、語言格式、語言多樣性和外部知識。此外,Zhang等人(2023)提出了一個多模態基準,重點關注幾何學。與我們的研究最相關的是MATH(Hendrycks et al., 2021)和Theoremqa(Chen et al., 2023)基準。盡管提供了各種主題的數學問題,但它們的范圍比我們的基準要窄得多,并且沒有為每個問題提供詳細的主題細分。此外,最近的一項工作(Toshniwal et al., 2024)已經開始為LLMs的指令調優生成大規模的合成數學基準。
LLMs與數學
近年來,LLMs在數學推理方面取得了顯著成就(Srivastava et al., 2022;Liu et al., 2023)。這些成就得益于旨在提升LLMs性能的方法,主要通過分解推理。這些策略受到人類問題解決過程的啟發,包括提供逐步指導(Wei et al., 2022;Yao et al., 2024;Besta et al., 2023)、采用驗證機制以提高模型的一致性和準確性(Weng et al., 2022),以及結合復雜的推理策略(Qi et al., 2023)。
6.結論
本文對LLMs的數學推理進行了全面評估。我們創建了數學主題樹(MaTT)基準,一個具有挑戰性且系統組織的基準,提出了一系列涵蓋廣泛數學科目的問題,每個問題都與詳細的分層結構主題相關。通過探索LLMs在MaTT上的準確性,我們觀察到它們在廣泛的數學主題上表現掙扎,特別是在沒有多項選擇選項的情況下。我們還觀察到LLMs在不同主題上的表現差異,以及思維鏈提示并未顯著改進性能。為了調查模型性能的差距,我們手動分析了它們回答問題時的解釋。我們發現,GPT-4在提供正確答案的實例中,只有53.3%的解釋被認為是完整的。此外,我們觀察到模型在解決簡單問題時表現較好,而在處理更復雜問題時則采用替代策略。這表明LLMs在進行深度、創造性和復雜數學思維方面存在根本性的差距。我們將公開與MaTT基準相關的所有代碼、注釋和數據。
7.局限性
本研究提出了幾個在解釋研究結果時應考慮的局限性。
首先,我們使用MaTT基準僅對三種廣泛采用的LLMs進行了數學推理能力評估。這一有限的模型選擇可能無法完全代表LLMs的多樣化能力。在未來的評估中納入更多種類的模型,可以更全面地理解LLMs在不同架構和訓練模式下的數學推理能力。
其次,我們評估模型推理能力的方法主要依賴于分析其自生成的解釋。雖然這種方法使我們能夠評估模型如何推理其答案,但它本身存在潛在的偏見和不準確性。LLMs提供的解釋可能并不總是準確反映其潛在的推理過程,有時甚至可能具有誤導性或不完整性。采用更客觀或多樣化的評估方法可能是必要的,以更清晰和準確地了解LLMs如何處理和解決數學問題。
Gholami Davoodi A, Pouyan Mousavi Davoudi S, Pezeshkpour P. LLMs Are Not Intelligent Thinkers: Introducing Mathematical Topic Tree Benchmark for Comprehensive Evaluation of LLMs[J]. arXiv e-prints, 2024: arXiv: 2406.05194.
Carnegie Mellon University, Megagon Labs
本文轉載自公眾號AIRoobt ,作者:AIRoobt
原文鏈接:??https://mp.weixin.qq.com/s/MCXBX9qH2s5dkaDeLYlL1w??

















