你是否思考過：大模型是如何做到既能到出口成章又能演算數學題的呢？今天，讓我們用實例來揭開大模型中「思維鏈」的神秘面紗。

1、什么是思維鏈技術？

簡而言之，思維鏈技術就是讓大模型在回答問題時，不再只給你一個冰冷的答案，而是會抽絲剝繭般地一步步展示它是如何找到答案的。

要知道，傳統 LLM 的訓練目標是預測下一個 token，而不是系統地推理數學問題。它們在龐大的文本語料庫中學到了各種模式，但「數學公式的嚴謹推演」并非其主要任務。就好比一個狂熱的小說家，擅長講故事，卻不能推演平面幾何。

過去模型常常「一口氣出答案」，讓人不知其所以然；而引入思維鏈后，大模型開始認真剖析問題，像個老學究一樣，慢慢盤點每個推理步驟、思路和細節，甚至讓問題解決過程變得豐富多彩。

看問題：“9.9 和 9.11 哪個大？”

這個問題你一定很眼熟，以往的 LLM 模型往往一口氣給出答案：

“9.9 大” 或者 “9.11 大”

相信大家都見過上面這類問答。

而有思維鏈加持的大模型會類似下面這樣回答：

[思維鏈開始]
  步驟 1： 比較整數部分，9.9 和 9.11 的整數部分均為 9，相等。
  步驟 2： 比較小數部分。將 9.9 補零為 9.90，與 9.11 對齊小數位數。
  步驟 3： 比較十分位：9.90 的十分位是 9，9.11 的十分位是 1，9 > 1。
  步驟 4： 由于十分位已分出大小，無需繼續比較后續位數。
[思維鏈結束]
 最終答案： 9.9 更大

當然，像“步驟 n：” 之類的文字不需要出現在最終的回答中。

我們生活中的很多問題都不是簡單的“一步到位”。大到規劃一場旅行，小到如何在朋友圈中秀出你的“高情商”，都需要多步驟好好斟酌。大模型也是如此，只有通過多步推理，才能理解問題的復雜性，給出更準確、更合理的回復。

研究者們發現，當讓模型生成中間過程時，它不僅局限于直接回憶知識，而是利用內在邏輯「自行推演」出合理的答案。這就像你的大腦：遇到難題時，你會先喊「冷靜思考」，然后按部就班地分解問題。

一個例子

模型被問到：“你覺得豬能飛嗎？”傳統回答：直接回答“不會”（語氣平淡，仿佛沒有看過《哪吒之魔童鬧海》）。

然而，啟用了思維鏈后，模型會這樣戲劇性地展開思考：

步驟 1： 回顧常識 —— 豬通常不會飛，畢竟它們天生厚重大氣。（想象一下豬穿著小翅膀在天空飄，滑稽得像動畫！）

步驟 2： 考慮例外 —— 有沒有可能在特定情境下實現“豬飛”？比如某部科幻電影里，通過改造、生物工程讓豬擁有了噴氣式翅膀。

步驟 3： 分析科技現實 —— 目前的技術還沒能讓豬飛起來，畢竟重力太強，哪怕是超級英雄也得靠電影特效。

最終結論： 豬會飛只存在于你的夢里或者奇幻小說中，而在現實生活中，我們只能默默哀嘆：“豬還是不飛，老天對它們太仁慈了。”

這樣的回答不僅邏輯清晰，還充滿幽默感，既讓人啼笑皆非，又能學到知識。可以說，思維鏈使得模型回答從“僵硬的機器式”變得幾乎像個會講笑話的談話高手。

更有意思的是，這種方法還可以幫助模型發現潛在的細節錯誤。如果中間某一步出錯了，那么后續的流程也會暴露問題，從而促使模型進行自我修正！這就好比你在煮咖啡時突然發現多加了一勺咖啡粉，結果導致風味失調。

2、嚴肅一點講

思維鏈（Chain of Thought, CoT）是一種提示策略，通過在輸入提示中提供一系列中間推理步驟，引導大型語言模型逐步思考并生成最終答案。與傳統的直接提問方式相比，CoT 模仿了人類的思考過程：在面對復雜問題時，通常會將問題分解為多個小步驟，逐一解決，最終得出結論。

CoT 的核心思想在于：通過顯式地展示推理過程，幫助模型更好地理解問題的結構和邏輯，從而提升其在需要多步推理的任務中的表現。

例如，在解決數學問題時，CoT 不僅要求模型給出答案，還要求其展示演算和推理過程；在常識推理中，CoT 幫助模型通過邏輯鏈條得出更合理的結論。

首先，CoT 也是在傳統 LLM 的任務框架下行事，即預測下一個 token。那么它怎么做到植入推理過程呢？

下面我們以一個具體案例，從 LLM 模型的輸入和輸出角度，來解釋思維鏈在算法層面的工作原理。

這個例子不僅展示了模型如何從輸入生成中間推理步驟（即思維鏈 tokens），再輸出最終答案，而且也揭示了這些過程背后的大致算法機制。

案例 1：計算表達式

請計算：  

有思維鏈加持的大模型回答起來可能輸出如下文本：

[思維鏈開始]
步驟 1：首先計算括號內的加法，3 + 5 = 8。
步驟 2：然后將結果乘以 2，8 × 2 = 16。
步驟 3：接著減去 4，16 - 4 = 12。
步驟 4：最后，除以 2，12 ÷ 2 = 6。
[思維鏈結束]
最終答案：6

上面是大致樣子，鏈的具體形式當然是靈活的。

下面是算法層面的詳細解釋：

1. 輸入與分詞

• 輸入文本：用戶輸入的文本為??請計算：((3+5) * 2 - 4)/2??
• 分詞與編碼：模型首先將這段文本分解為一系列的單詞或符號（也稱為“tokens”），例如：[ \text{["請", "計算", "：", "(", "(", "3", "+", "5", ")", "*", "2", "-", "4", ")", "/", "2"]} ] 接著，每個 token 都被映射成一個高維向量，輸入到 Transformer 編碼器中。

2. 隱藏狀態與模型推理

• Transformer 編碼器：經過多層自注意力（self-attention）和前饋神經網絡，這些 token 的向量得到了上下文敏感的表示（隱藏狀態）。這些隱藏狀態為之后的生成過程提供了充分的“記憶”和語境。
• 提示與解碼：當模型開始生成回答時，通常會使用一種解碼器機制（如貪心搜索或束搜索），它逐步生成文本 tokens。– 在傳統模式下，模型可能直接生成最終答案 “6”。– 而采用鏈式思維提示后，模型被引導生成一系列中間推理步驟。這些步驟就是“思維鏈” tokens，例如：

a.“步驟 1：...”

b.“步驟 2：...”… 依次生成，直到完成問題求解。

3. 輸入與輸出的完整路徑示意

下面用一個簡單的 ASCII 流程圖展示整個過程：

++
|       用戶輸入文本          |
| "請計算：((3+5)*2-4)/2"     |
++
             │
             ▼
++
|         分詞 & 編碼         |
|  Tokenization & Embedding   |
++
             │
             ▼
++
|    Transformer 編碼器      |
|   生成上下文感知的隱藏狀態     |
++
             │
             ▼
++
|        解碼過程:            |
| 生成中間的 Chain-of-Thought   |
|（步驟 1、步驟 2、… 推理過程）    |
++
             │
             ▼
++
|   生成最終答案 Output Tokens  |
|           “6”             |
++

從算法角度看，思維鏈相當于為 LLM 增加了一個「推理草稿紙」：

• 輸入階段：用戶問題經過分詞和編碼，生成隱藏狀態。
• 生成階段：模型被引導生成中間「草稿」，描述每一步推理過程的 tokens 。
• 輸出階段：基于這些中間 tokens，最終匯總出正確答案的 tokens。

這種機制讓模型不僅能回答「多少」這樣的問題，而且能展示「為什么」，使回答過程邏輯嚴謹，仿佛一個會詳細講解思路的老師在旁輔導。通過對內部中間 tokens 的采樣和自我校驗，思維鏈讓復雜問題求解變得既透明又高效，真正打破了以往僅靠模式匹配的黑盒局限。

案例 2：微積分演算

在一些研究中，研究人員發現在解決復雜數學問題時，通過在提示中展示 3～5 個帶有詳細推理過程的示例，可以大幅度提高模型正確率；而在專門針對數學或邏輯推理問題進行微調時，常見的做法是構建包含數千到上萬個示例的數據集。這些數據集幫助模型建立起「在解題過程中先明確中間狀態，再得出結論」的推理習慣。

舉例來說，假設我們希望模型學會解決微積分中的積分問題，數據集中可能包括了從建立積分公式、變量替換、積分分步計算、再到最后化簡的完整過程。

以一題簡單的不定積分為例，數據集示例可能這樣構造：

問題：計算 ∫ (2x * cos(x2)) dx  
推理過程：
  步驟1：注意到 x2 的導數是 2x，因此做變量替換設 u = x2；  
  步驟2：則 du = 2x dx，故原積分可寫為 ∫ cos(u) du；  
  步驟3：積分 ∫ cos(u) du = sin(u) + C；  
  步驟4：將 u = x2 代回，得 sin(x2) + C  
最終答案：sin(x2) + C

類似的，稍微復雜一點的例子，如計算如下定積分。

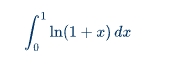
思維鏈示例如下：

推理過程：
 步驟 1：對積分采用分部積分法，設 u = ln(1+x)，dv = dx。
 步驟 2：則有 du = (1/(1+x)) dx，v = x。
 步驟 3：應用分部積分公式：∫ u dx = u·v - ∫ v du，
         得到：∫ ln(1+x) dx = x·ln(1+x) - ∫ [x/(1+x)] dx。
 步驟 4：注意到分式可以拆分：x/(1+x) = 1 - 1/(1+x)。
 步驟 5：因此 ∫ [x/(1+x)] dx = ∫ 1 dx - ∫ 1/(1+x) dx = x - ln|1+x| + C。
 步驟 6：綜合得：∫ ln(1+x) dx = x·ln(1+x) - x + ln|1+x| + C。
 步驟 7：將積分區間 0 到 1 帶入：
         當 x = 1 時：1·ln2 - 1 + ln2 = 2ln2 - 1；
         當 x = 0 時：0 - 0 + ln1 = 0。
 步驟 8：定積分結果為 (2ln2 - 1) - 0 = 2ln2 - 1。
最終答案：2ln2 - 1

構造像這樣的示例，如果多樣性和覆蓋面足夠，可能需要上千例才能讓模型全面掌握微積分問題的鏈式推理方法，但對于引導大型預訓練語言模型來說，再提供幾個樣例就能顯著激發它已有的能力。

對于像微積分這樣的復雜數學任務，若從零開始訓練讓模型形成清晰鏈式推理的能力，大規模的預訓練數據集中的「推理示例」可能達到數百萬 tokens，而在專門微調時數百到數千個高質量推理示例已足矣激發和穩固這項能力。

網絡規模與學習能力

這里有一點值得提一下，就是網絡規模在鏈式推理中扮演了重要角色。

小網絡的局限性：

• Token 級別關系：小型網絡受制于其參數數量和計算能力，往往只能捕捉到局部的、短程的 token 級別關系。它們擅長完成一些簡單的任務（如句子補全、短文本分類等），但在處理需要復雜邏輯推理和多步推導的問題時顯得力不從心。
• 上下文局限：小網絡在處理長文本時，可能會因為模型的容量限制，無法很好地記住或理解上下文關系。這導致其在多步驟推理過程中容易丟失重要信息或產生錯誤。

大網絡的優勢：

• 命題級別關系：大規模模型擁有更大的參數空間和更強的表示能力，可以捕捉到更復雜、長程的關系。這使得它們能夠更好地理解和生成鏈式推理中的中間步驟，類似于「命題級別」的邏輯推導。
• 增強的上下文理解：大網絡具備更強的上下文捕捉能力，可以在較長文本中保持一致性和連貫性。它們能在解決復雜問題時，保持對多步推理過程的記憶和邏輯鏈條的清晰展示。

具體示例對比

假設有一個復雜的數學問題，需要多個步驟才能求解：

小網絡可能生成的內容：

問題：計算 ∫ (2x * cos(x2)) dx
答案：這是一個復雜的積分問題，需要做變量替換。

• 缺陷：小網絡可能停留在簡單的描述上，無法具體展示變量替換和逐步積分的過程。

大網絡生成的內容：

問題：計算 ∫ (2x * cos(x2)) dx
步驟1：注意到 x2 的導數是 2x，因此做變量替換設 u = x2。
步驟2：則 du = 2x dx，故原積分可寫為 ∫ cos(u) du。
步驟3：積分 ∫ cos(u) du = sin(u) + C。
步驟4：將 u = x2 代回，得 sin(x2) + C。
答案：sin(x2) + C

• 優勢：大網絡能夠詳細展示每個中間步驟，邏輯清晰，確保問題求解過程透明且可驗證。

理論支持：在諸多研究中，比如 OpenAI 發表的關于 GPT-3 的論文，他們發現隨著網絡規模的增大，模型在復雜任務上的表現顯著提升。這不僅包括語言理解和生成，還涵蓋了邏輯推理和數學問題求解。大規模模型通過大量預訓練數據，學會了從簡單的 token 關系推導出更高階的邏輯模式，這正是鏈式推理得以實現的基礎。

思維鏈的有效訓練確實依賴于足夠大的網絡規模。小型網絡在學習和表現復雜邏輯鏈條方面存在天然的限制，而大規模網絡具備更強的表示能力和上下文理解力，可以在多步驟推理中展現出更好的性能。這個過程不僅需要龐大的模型參數，還依賴于大量高質量、多樣化的數據來強化和檢驗模型的推理能力。

3、總結

思維鏈技術正是利用了大模型生成下一個 token 的自回歸機制，讓模型在每一步輸出時都顯式地展示其「中間思考過程」。這意味著，當模型面對一個復雜問題時，它不再試圖一口氣生成最終答案，而是在生成過程中逐步展開邏輯步驟，類似于我們人類在思考問題時寫下草稿、一步步推理的過程。

這種機制的核心在于：

• 逐步展開:模型按順序生成中間步驟，每個步驟都為后續步驟提供了「上下文」，確保最終結論更具條理性和邏輯性。
• 透明推理:通過生成中間 tokens，思維鏈不僅提高了答案的準確性，也讓用戶可以看到模型的推理過程，從而增強了答案的可信度。
• 自我校驗:如果某個步驟出現邏輯漏洞，整個鏈條可能會暴露問題，使得模型有機會在后續生成中自我糾正。

總之，思維鏈技術利用 token 生成機制，讓大模型具備「按步驟解決問題」能力，也是為何在當前的很多復雜任務（比如數學題、邏輯推理）中，鏈式思維表現出了卓越的效果。

怎么樣，現在再去跟 DeepSeek-R1 之類的 AI 聊天，是不是心里更有底啦。

本文主要通過舉例子揭開思維鏈的神秘面紗，至于之后發展出來的更多衍生技術，如零樣本 CoT、自動 CoT 以及多模態 CoT 等，不在本文涉及范圍。

4、附錄

最后，為了加深對 LLM 的了解，我們再來舉例更多的數學相關的思維鏈數據集中的具體例子，結合了公開數據集中的典型問題和實際應用場景。

1）數列推理問題

問題：給定數列 1，2，6，24，120，? ，... 問號處的數字是多少？這個數列有什么數學意義？思維鏈：

• 步驟1：觀察數列的遞增規律：1 → 2（×2），2 → 6（×3），6 → 24（×4），24 → 120（×5）。
• 步驟2：發現每個數字是前一個數字乘以遞增的整數（2, 3, 4, 5…），因此下一個數應為 120×6 = 720。
• 步驟3：識別數列的數學意義：這是階乘數列（n!），即1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, 6! = 720。答案：720，數列為階乘數列。

2）多步驟數學應用題

問題：一個人有 16 個球，其中一半是高爾夫球，而高爾夫球中又有一半是藍色的。問有多少個藍色高爾夫球？思維鏈：

• 步驟 1：總高爾夫球數 = 16×? = 8 個。
• 步驟 2：藍色高爾夫球數 = 8×? = 4 個。答案：4 個藍色高爾夫球。

3）代數問題

問題：將 100 根火柴分成 10 堆，每堆數量為單數，且相鄰兩堆相差 2 根。如何分配？思維鏈：

• 步驟1：單數序列可從 1 開始，每次加 2，即 1,3,5,…,19。
• 步驟2：驗證總和：1+3+5+…+19 = (10 項等差數列求和) = 102 = 100。
• 步驟3：分配方案為 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 根。

4）視覺誤導下的數學驗證

問題：下圖中的兩個怪物看起來大小不同，但實際上是否相同？（需結合圖像）思維鏈：

• 步驟1：使用測量工具對比高度和寬度。
• 步驟2：分析視覺錯覺來源（如背景線條或透視效果）。
• 步驟3：確認兩者實際尺寸相同。答案：大小相同，視覺誤差由背景設計引起。

5）復雜數學推理（GSM8K 數據集示例）

問題：簡給媽媽 2 朵花后剩下 10 朵，接著給爸爸 3 朵，爸爸現在有多少朵花？思維鏈：

• 步驟1：簡最初有花數 = 10+2 = 12 朵。
• 步驟2：給媽媽后剩余 10 朵，再給爸爸 3 朵，則爸爸有 3 朵。
• 步驟3：注意問題中的“給爸爸后他會有多少朵”，而非簡剩余多少。答案：3 朵。

6）數值比較與符號推理

問題：為什么大模型可能錯誤認為 9.11 大于 9.9？思維鏈：

• 步驟1：模型將 “9.11” 切分為 “9”、“.”、“11”，而 “9.9” 切分為 “9”、“.”、“9”。
• 步驟2：模型誤將 “11” 與 “9” 直接比較，導致錯誤結論。
• 步驟3：通過 CoT 提示，模型需逐步比較小數點后位數：9.11 = 9 + 0.11，9.9 = 9+0.9→0.9 > 0.11。答案：9.9 更大。

7）字母計數任務

問題：單詞 “strawberrrrry” 中有多少個字母 “r”？思維鏈：

• 步驟1：逐個字母拆分：s-t-r-a-w-b-e-r-r-r-r-r-y。
• 步驟2：標記每個 “r” 的位置（第 3、7、8、9、10、11 位）。答案：6 個 “r”。

本文轉載自機器學習與數學，作者： 大師兄