解析從堆到優(yōu)先隊(duì)列的實(shí)現(xiàn)
優(yōu)先隊(duì)列,顧名思義,就是一種根據(jù)一定優(yōu)先級(jí)存儲(chǔ)和取出數(shù)據(jù)的隊(duì)列。它可以說是隊(duì)列和排序的***結(jié)合體,不僅可以存儲(chǔ)數(shù)據(jù),還可以將這些數(shù)據(jù)按照我們?cè)O(shè)定的規(guī)則進(jìn)行排序。
先說說優(yōu)先隊(duì)列的實(shí)現(xiàn)吧。有一點(diǎn)需要澄清,很多人一直以為Priority Queue就是一個(gè)Priority Heap,這種說法當(dāng)然是片面的。既然優(yōu)先隊(duì)列只是存儲(chǔ)數(shù)據(jù)和排序的結(jié)合,那么根據(jù)我們學(xué)過的知識(shí),可以列出以下的實(shí)現(xiàn)方法:無序數(shù)組、無序鏈表、有序數(shù)組、有序鏈表以及二叉查找樹,當(dāng)然還有堆。這些方法在實(shí)現(xiàn)中當(dāng)然也有優(yōu)先級(jí),下表就是一些方法的實(shí)現(xiàn)基本操作的時(shí)間性能對(duì)比:
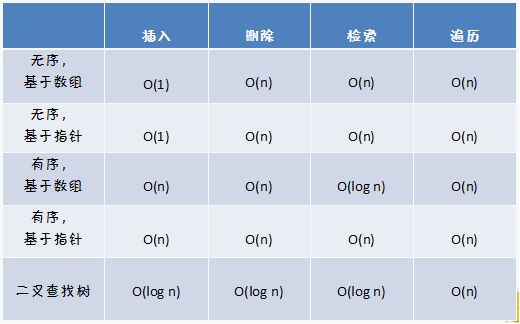
圖1 一些優(yōu)先隊(duì)列的實(shí)現(xiàn)方案的時(shí)間性能對(duì)比
從這張表里我們可以按照時(shí)間復(fù)雜度這個(gè)優(yōu)先級(jí)來進(jìn)行一次排序,當(dāng)然,你會(huì)選用***一種二叉查找樹作為實(shí)現(xiàn)優(yōu)先隊(duì)列的方案,但是實(shí)際上我們采用的是堆。堆,就是一種二叉樹,堆和二叉查找樹是類似的,但是也有些許不同:從形狀來看,二叉查找樹可以有不同的形狀,而堆只能是完全二叉樹;在時(shí)間性能上,二者并無明顯的區(qū)別。堆也是有序的,我們一般將其分為大頂堆和小頂堆。小頂堆,顧名思義,就是這個(gè)堆的子結(jié)點(diǎn)的值小于父結(jié)點(diǎn)的值;相反的,大頂堆就是堆的子結(jié)點(diǎn)的值都大于父結(jié)點(diǎn)的值。
在實(shí)現(xiàn)的時(shí)候,我們常常使用基于數(shù)組的堆,即堆中的元素保存在一個(gè)數(shù)組中,而這個(gè)數(shù)組元素的保存也是按照一定規(guī)律的:如果父結(jié)點(diǎn)的位置為n,那么,其對(duì)應(yīng)的左右子結(jié)點(diǎn)的位置分別是2n+1和2n+2。也就是說,我們?cè)谝曈X上(如果用畫圖形象化表示堆的話)和本質(zhì)上將堆打扮成兩種東西,這樣既便于理解,也利于實(shí)現(xiàn),本質(zhì)的實(shí)現(xiàn)是用數(shù)組是因?yàn)榭紤]到數(shù)組的一些性能。
堆有兩個(gè)很基本的操作:增加、刪除。先來說說增加元素,假設(shè)有下面這樣一個(gè)堆:
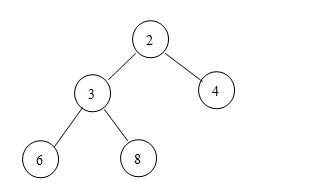
這時(shí)候,有一個(gè)元素1要添加進(jìn)來,這時(shí)候應(yīng)該怎么辦呢?***步,將元素添加到堆的***一個(gè)位置:
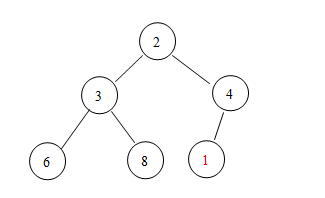
第二步,將新加入的元素與其父結(jié)點(diǎn)的值進(jìn)行比較,若新結(jié)點(diǎn)的值比其父結(jié)點(diǎn)的值要小(就像這個(gè)例子一樣),那么,交換兩個(gè)結(jié)點(diǎn)的值,重復(fù)第二步,直到形成一個(gè)小頂堆:
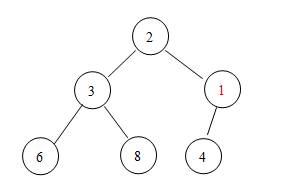
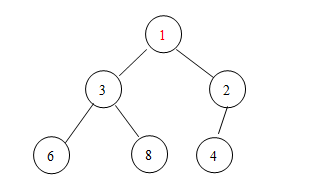
這樣,一個(gè)新的小頂堆誕生了!
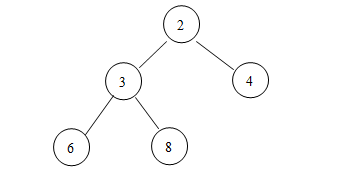
然后就是從堆中刪除一個(gè)元素了,假設(shè)在這個(gè)新的小頂堆中,我們打算刪除值為1的那個(gè)結(jié)點(diǎn):
***步,將這個(gè)1刪掉,假設(shè)其結(jié)點(diǎn)上當(dāng)前沒有值:
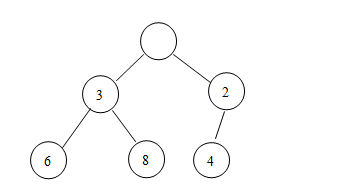
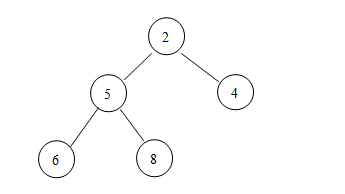
第二步,比較該刪除結(jié)點(diǎn)(當(dāng)前是最上面的那個(gè))的兩個(gè)子結(jié)點(diǎn),看誰的值小,交換其中較小值和這個(gè)空結(jié)點(diǎn)的值(假設(shè)是null),然后重復(fù)這一步,直到該空值到最小面一行:
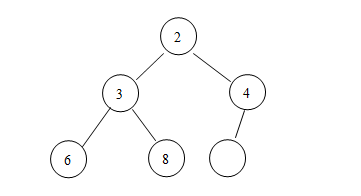
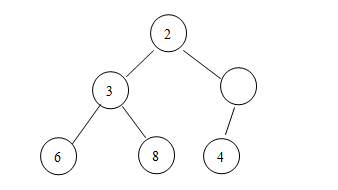
第三步,就是將這個(gè)空的結(jié)點(diǎn)從視線中移除了,這樣,刪除的過程就告一段落了(好吧,這個(gè)堆又回到解放前了)!
知道了這些基本的原理,對(duì)數(shù)據(jù)量更大的增加和刪除也應(yīng)該是觸類旁通了吧。
有人會(huì)質(zhì)疑堆中除堆頂元素之外的其他元素的順序問題:
比如這里為什么4會(huì)放在5的右邊兄弟結(jié)點(diǎn)上,這明顯是受了二叉查找樹的影響,因?yàn)槎褜?duì)我們來說,一般只有堆頂元素有用,因此只要保證堆頂元素是最小的就行了(對(duì)小頂堆)。
下面,簡(jiǎn)單介紹一下sun提供的PriorityQueue的一些基本的方法,以此來較為深入地理解優(yōu)先隊(duì)列的實(shí)現(xiàn)機(jī)制:
1.下面是PriorityQueue的聲明的***句話:
![]()
這句話表明:sun提供的優(yōu)先隊(duì)列是基于優(yōu)先堆實(shí)現(xiàn)的;
2.下面是聲明一個(gè)Object數(shù)組時(shí)的注釋:

由此可知,堆中的元素在數(shù)組中的保存方案;并且隊(duì)列中的優(yōu)先級(jí)最小的元素總是保存在queue[0]中,前提是該優(yōu)先隊(duì)列不為空。
下面是往PriorityQueue中上濾的方法:

這段代碼中,k代表當(dāng)前加入元素的位置,即***一個(gè)位置+1,x表示要添加的元素。首先得到父結(jié)點(diǎn)的值,然后將x的值和父結(jié)點(diǎn)的值進(jìn)行比較,如果子結(jié)點(diǎn)的值大于父結(jié)點(diǎn)值,不作更改,否則交換兩者的值。這個(gè)方法主要用于添加元素的時(shí)候。與之相對(duì)應(yīng)的有一個(gè)下濾方法siftDownComparable(),其功能是向下比較,用在刪除元素的實(shí)現(xiàn)中;
接下來就講添加元素的實(shí)現(xiàn):

這里可以看到用到了siftUp方法,其實(shí),siftUp中分情況調(diào)用了 siftUpUsingComparator()、siftUpComparable()。這在剛才已經(jīng)介紹了上濾的實(shí)現(xiàn)了。這里的添加元素就是上濾的過程。
當(dāng)然,我們?cè)谑褂脮r(shí),一般使用的方法是這三種:add、poll以及peek,add用以添加元素,其內(nèi)部是用offer方法實(shí)現(xiàn)的,peek用來得到堆頂元素,但是不刪除,而poll在返回堆頂元素之后,將堆頂元素刪除。
以上只是對(duì)優(yōu)先隊(duì)列的簡(jiǎn)要介紹,作為一個(gè)應(yīng)用比較廣泛的數(shù)據(jù)結(jié)構(gòu),優(yōu)先隊(duì)列還有許許多多奇妙的地方,它們都等著你去發(fā)現(xiàn)。
原文鏈接:http://februus.iteye.com/blog/1288305
【編輯推薦】






































