0x00 前言

慕容在生活和工作中常常會遇到一些十分迷信機(jī)器的人，他們之中很多人都相信機(jī)器是最理智的，沒有任何感情，是真正的鐵面無私，因此機(jī)器的運算所給出 的答案總是正確的，如果答案錯誤，那么一定是操作機(jī)器的人的問題。但機(jī)器的運算就一定是正確的嗎？事實上，機(jī)器出現(xiàn)運算錯誤并不是一個罕見的情況，一個典 型的例子便是小數(shù)運算。下面就讓我們來聊一個相關(guān)的話題，在機(jī)器或者具體的說在C#語言中小數(shù)是如何被處理的？

[[153323]]

0x01 先從一個“錯誤”的答案說起

 既然要聊一聊機(jī)器是怎么把算術(shù)題做錯的，那么我們自然要先來看一個機(jī)器運算錯誤的小例子。

#include <stdio.h> 
 
void main(){ 
    float num; 
    int i ; 
    num = 0; 
    for(i = 0; i < 100; i++) 
    { 
        num += 0.1; 
    } 
    printf("%f\n", num); 
} 

這是一份C語言寫成的小程序，邏輯十分簡單易懂，所要實現(xiàn)的結(jié)果無非是將0.1相加100次之后再輸出。我想不需要計算機(jī)來計算，我們自己心算就能立刻得出答案——10。那么計算機(jī)會交給我們一份什么樣的答案呢？下面我們將這份C代碼編譯并且運行一下。

答案一輸出，就讓人大吃一驚。怎么計算機(jī)還不如人的心算嗎？如果按照慕容在前言中提到的那些朋友這時可能就開始糾結(jié)是否是代碼寫錯了，亦或者是慕容 的電腦出現(xiàn)了什么問題。但事實上代碼是正確的，機(jī)器也是運行如常的。那么究竟是為什么計算機(jī)的運算輸給了人的心算呢？這就引出了下一個問題，計算機(jī)是如何 處理小數(shù)的呢？如果我們了解一下計算機(jī)處理小數(shù)的機(jī)制，那么這一切的迷就能夠解開了。（當(dāng)然如果有朋友用C#來對0.1加100次，之后的結(jié)果是10。但 那是C#在幕后為我們做的一些隱藏工作，在計算機(jī)處理小數(shù)的問題上，本質(zhì)是一樣的）。

0x02 數(shù)字的格式

一個程序可以看做是現(xiàn)實世界的一個數(shù)字化的模型。現(xiàn)實世界中的一切都可以轉(zhuǎn)化為數(shù)字在計算機(jī)的世界中重新復(fù)活。因此，一個不得不解決的問題就是數(shù)字是如何在計算機(jī)中表達(dá)的。這也是數(shù)字格式出現(xiàn)的意義。

眾所周知，機(jī)器語言全部都是數(shù)字，但是本文自然不會關(guān)心全部的二進(jìn)制格式。這里我們只關(guān)心現(xiàn)實中有意義的數(shù)字是如何在計算機(jī)中被表示的。簡單而言，有意義的數(shù)字大體可以分為以下三種格式。

整數(shù)格式

我們在開發(fā)的過程中遇到的大部分的數(shù)字其實都是整數(shù)。而整數(shù)在計算機(jī)中也是最容易表示的一種。我們遇到的整數(shù)都可以使用32位有符號整數(shù)來表示（Int32)。當(dāng)然，如果需要，還有有符號 64 位整數(shù)數(shù)據(jù)類型（Int64）可供選擇。至于和整數(shù)相對應(yīng)的便是小數(shù)，而小數(shù)主要有兩種表示方式。

定點格式

所謂定點格式，即約定機(jī)器中所有數(shù)據(jù)的小數(shù)點位置是固定不變的。而定點小數(shù)的最常見的例子是SQL Server中的money類型。事實上定點小數(shù)已經(jīng)很不錯了，它顯然能夠適合很多需要處理小數(shù)的情況。但是它有一個與生俱來的缺點，那就是由于小數(shù)點的 位置固定，因此它能表示范圍是受限的。因此下面我們本文的主角就要出場了。

浮點格式

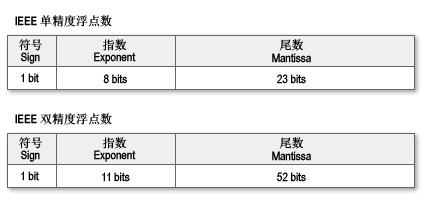
解決定點格式先天問題的方案便是浮點格式的出現(xiàn)。而浮點格式的組成則包括符號、尾數(shù)、基數(shù)和指數(shù)，通過這四部分來表示一個小數(shù)。由于計算機(jī)內(nèi)部是二 進(jìn)制的，因此基數(shù)自然而然是2（就如十進(jìn)制的基數(shù)是10一樣）。因此計算機(jī)在數(shù)據(jù)中往往無需記錄基數(shù)（因為總是2），而是只用符號、尾數(shù)、指數(shù)這三部分來 表示。很多編程語言都至少提供了兩種使用浮點格式表示小數(shù)的數(shù)據(jù)類型，即我們常常能見到的雙精度浮點數(shù)double和單精度浮點數(shù)float。同樣，在我 們的C#語言中也存在著這兩種使用了浮點格式表示小數(shù)的數(shù)據(jù)類型——按照C#語言標(biāo)準(zhǔn)雙精度浮點數(shù)和單精度浮點數(shù)在C#中對應(yīng)的是 System.Double和System.Single。但是事實上在C#語言中還存在著第三種使用了浮點格式表示小數(shù)的數(shù)據(jù)類型，那就是 decimal類型——System.Decimal。需要注意的是，浮點格式的表示形式有很多，而在C#中遵循的是IEEE 754標(biāo)準(zhǔn)：

• float單精度浮點數(shù)為32位。32位的構(gòu)造為：符號部分1bit、指數(shù)部分8bit以及尾數(shù)部分23bit。

• double雙精度浮點數(shù)為64位。64位的構(gòu)造為：符號部分1bit、指數(shù)部分11bit以及尾數(shù)部分52bit。

0x03 表示范圍、精度和準(zhǔn)確度

既然聊完了數(shù)字在計算機(jī)中的幾種表示形式，那么接下來我們就不得不提一下在選擇數(shù)字格式時的一些指標(biāo)。最常見的無非是這幾點：表示范圍、精度、準(zhǔn)確度。

數(shù)字格式的表示范圍

顧名思義，數(shù)字格式的表示范圍指的就是這種數(shù)字格式所能表示的最小的值到***的值的范圍。 例如一個16位有符號整數(shù)的表示范圍是從-32768到32767。如果要被表示的數(shù)字的值超出了這個范圍，那么使用這種數(shù)字格式就不能正確的表示這個數(shù) 字了。當(dāng)然在這個范圍內(nèi)的數(shù)字也有可能無法被正確的表示，例如16位有符號整數(shù)是無法準(zhǔn)確表示一個小數(shù)的，但是總有一個接近的值是可以用16為有符號整數(shù) 格式來表示的。

數(shù)字格式的精度

實話實說，精度和準(zhǔn)確度讓很多人都有一種十分模糊的感覺，似乎是一樣的卻又有區(qū)別。但慕容需要提醒各位注意的是，精度和準(zhǔn)確度是兩個有巨大差距的概念。

通俗的來講，數(shù)字格式的精度可以認(rèn)為是該格式有多少信息用來表示一個數(shù)字。更高的精度通常意味著能夠表示更多的數(shù)字，一個最明顯的例子便是精度越高 那么這種格式所能表示的數(shù)字就越接近真實的數(shù)字。例如我們知道1/3如果換算成小數(shù)0.3333....是無窮盡的，那么它在五位精度的情況下可以寫成 0.3333，而在七位的情況下就又變成了0.333333（當(dāng)然，如果用七位表示五位，那么就是0.333300)。

數(shù)字格式的精度還會影響到計算的過程。舉一個簡單的例子，如果在計算中我們使用的是一位精度。那么整個計算可能就變成了下面的這種情況：

0.5 * 0.5 + 0.5 * 0.5 = 0.25 + 0.25 
 
                                = 0.2 + 0.2 
 
                                =0.4 

而如果我們使用的是兩位精度，那么計算過程又會變成下面的情況。

0.5 * 0.5 + 0.5*0.5 = 0.25 + 0.25 
 
　　　　　　　　　　 =0.5 

對比兩種精度情況下的計算結(jié)果，一位精度情況下的計算結(jié)果和正確的結(jié)果差了0.1。而使用了兩位精度的情況則正常的計算出了結(jié)果。因此可以發(fā)現(xiàn)在計算的過程中保證精度是一件多么有意義的事情。

數(shù)字格式的準(zhǔn)確度

數(shù)字格式的表示范圍、精度都已經(jīng)介紹完了，那么接下來我們就來介紹一下數(shù)字格式的準(zhǔn)確度。剛剛已經(jīng)說過了，準(zhǔn)確度和精度是一對經(jīng)常讓人混淆的概念。

那么我們再通俗的給準(zhǔn)確度來個注釋，簡單的說它表示的是該數(shù)字格式（特定環(huán)境）所表示的數(shù)字和真實數(shù)字的誤差。準(zhǔn)確度越高，則意味著數(shù)字格式所表示的數(shù)字和真實數(shù)字的值之間的誤差越小。準(zhǔn)確度越低，則意味著數(shù)字格式所表示的數(shù)字和真實數(shù)字的值之間的誤差越大。

需要注意的一點是數(shù)字格式的精度和數(shù)字格式的準(zhǔn)確度并沒有直接的關(guān)系，這一點也是很多朋友在概念上常常會混淆的地方。使用低精度的數(shù)字格式表示的數(shù)字，并不一定要比使用高精度的數(shù)字格式所表示的數(shù)字的準(zhǔn)確度低。

舉一個簡單的例子：

Byte   num = 0x05; 
Int16  num1 = 0x0005; 
Int32  num2 = 0x00000005; 
Single num3 = 5.000000f; 
Double num4 = 5.000000000000000; 

此時，我們分別使用5種不同的數(shù)字格式表示同一個數(shù)字5，雖然數(shù)字格式的精度（從8位到64位）不同，但是通過數(shù)字格式所表示出來的數(shù)和真實的數(shù)是一樣的。也就是說對于數(shù)字5，這5種數(shù)字格式的準(zhǔn)確度相同。

0x04 取整誤差

了解了計算機(jī)中常見的幾種數(shù)字格式之后，現(xiàn)在我們再來聊一聊計算機(jī)是如何通過數(shù)字格式來表示現(xiàn)實世界中的數(shù)字的。眾所周知，計算機(jī)中使用的是0和 1，即二進(jìn)制，使用二進(jìn)制表示整數(shù)是十分容易的一件事情，不過在使用二進(jìn)制表示小數(shù)時，我們往往會產(chǎn)生一些疑問。例如二進(jìn)制小數(shù)1110.1101換算成 十進(jìn)制是多少呢？***眼看上去多了一個小數(shù)點，似乎讓人十分困惑。事實上它的處理和整數(shù)是一樣的，即將各個數(shù)位的數(shù)值和位權(quán)相乘結(jié)果求和。小數(shù)點前的位 權(quán)，大家都已經(jīng)十分熟悉了，從右向左分別是0次冪、1次冪、2次冪以此遞增，因此小數(shù)點前的二進(jìn)制換算為十進(jìn)制便是：

1 * 8 + 1 * 4 + 1 * 2 + 0 = 14 

而在小數(shù)點之后的位權(quán)，相應(yīng)的從左向右分別是-1次冪、-2次冪依次遞減。因此小數(shù)點之后的二進(jìn)制轉(zhuǎn)換為十進(jìn)制便是：

1 * 0.5 + 1 * 0.25 + 0 * 0.125 + 1 * 0.0625 = 0.8125 

因此1110.1101這個二進(jìn)制小數(shù)轉(zhuǎn)換為十進(jìn)制便是14.8125。

通過觀察小數(shù)點之后的二進(jìn)制轉(zhuǎn)換為十進(jìn)制的過程，各位看官是否發(fā)現(xiàn)了很有趣的一個事實呢？那就是小數(shù)點之后的二進(jìn)制并不能表示所有的十進(jìn)制數(shù)，換言 之有一些十進(jìn)制數(shù)是無法轉(zhuǎn)換成二進(jìn)制的。這個很好理解，因為小數(shù)點之后，二進(jìn)制的位權(quán)按照除以2的節(jié)奏遞減，而十進(jìn)制卻是按照除以10的節(jié)奏遞減。因此如 果小數(shù)點后4位用二進(jìn)制表示，即從.0000~.1111這個范圍內(nèi)連續(xù)的二進(jìn)制數(shù)值事實上對應(yīng)的十進(jìn)制數(shù)是不連續(xù)的，所有可能的結(jié)果也不過是各個位權(quán) （0.5、0.25、0.125以及0.0625）相加的組合而已。

因此，一個在十進(jìn)制中十分簡單的數(shù)字如果用二進(jìn)制來準(zhǔn)確無誤的表示，所使用的位數(shù)可能會十分長甚至是***的。一個很好的例子便是使用二進(jìn)制浮點數(shù)來表示十進(jìn)制中的0.1：

事實上變量x中所保存的值并不是真正的十進(jìn)制中的0.1，而是一個最接近十進(jìn)制0.1的二進(jìn)制浮點數(shù)。這是因為無論小數(shù)點之后有多少位二進(jìn)制的數(shù)，2的負(fù)數(shù)次冪都無法相加得到0.1這個結(jié)果，因此0.1這個十進(jìn)制數(shù)在二進(jìn)制中會變成一個***小數(shù)。

當(dāng)然二進(jìn)制有可能無法準(zhǔn)確的表示一個十進(jìn)制小數(shù)很好理解，因為這有點類似于在十進(jìn)制中我們同樣無法準(zhǔn)確表示1/3這樣的循環(huán)小數(shù)。

此時，我們便不得不和計算機(jī)妥協(xié)了。因為我們現(xiàn)在知道了在計算機(jī)中使用的數(shù)值可能并不等于真實世界中的數(shù)值，而是計算機(jī)使用某種數(shù)字格式表示的一個 十分接近原始數(shù)字的一個值。而在整個程序運行的過程中，我們的計算機(jī)就要一直使用這個僅僅是近似的數(shù)值來參與計算，我們假設(shè)真實的數(shù)值是n，而計算機(jī)事實 上會使用另一個數(shù)值n + e（當(dāng)然e是一個可正可負(fù)且十分小的數(shù)）來參與計算機(jī)中的運算。此時，這個數(shù)值e便是取整誤差。

而這還僅僅是一個數(shù)字在計算機(jī)中使用近似值來表示，如果該數(shù)值參與到計算中去，那么顯然會帶來更多誤差。這也是本文一開始那個c程序之所以計算錯誤 的原因，因為無法正確的表示參與計算的值，到***都變成了近似值。當(dāng)然C#語言相對而言要“高級”了很多，雖然在計算機(jī)中也是近似值，但是展示在大家眼前 的至少還是更加符合人們“預(yù)期”的值。不過在C#中，小數(shù)計算真的是不會出錯的嗎？畢竟，這一切似乎僅僅是障眼法。

0x05 取與舍，C#的小數(shù)

比比是否相等

不知道各位看官在使用一些關(guān)系運算符時，有沒有留意到直接使用等號比較兩個小數(shù)是否相等時是否會出現(xiàn)一些意想不到的問題。我身邊的朋友使用關(guān)系運算 符直接比較兩個小數(shù)大小的情況比較多，而直接比較兩個小數(shù)是否相等的情況卻不太多。同時我在此也想提醒各位***不要輕易比較兩個小數(shù)是否相等，即便在C# 這種高級語言中仍然可能得到讓人感覺“錯誤”的答案，這是因為我們事實上比較的是兩個小數(shù)是否“接近”于相等，而不是兩個數(shù)是否是真正的相等。下面這個例 子可能會更好的說明這一點：

using System; 
 
class Test 
{    
    static void Main() 
    { 
        double f = Sum (0.1d, 0.2d); 
        double g = 0.3d; 
        Console.WriteLine (f); 
        Console.WriteLine (f==g); 
    } 
    
    static double Sum (double f1, double f2) 
    { 
        return f1+f2; 
    } 
} 

我們編譯并且運行這段代碼，可以看到輸出了如下的內(nèi)容：

比較這兩個小數(shù)的結(jié)果并不是true，這和我們的預(yù)期并不一樣。

浮點數(shù)的真模樣

我們知道，像上文中的那個二進(jìn)制小數(shù)1110.1101事實上也是按照人類習(xí)慣表達(dá)出來的，但是計算機(jī)可是不能識別這種帶小數(shù)點的東西的哦。所以計 算機(jī)會使用之前介紹的數(shù)字格式來表示這樣一個數(shù)字，那么一個二進(jìn)制浮點數(shù)在計算機(jī)中到底是如何表現(xiàn)的呢？其實在上文介紹數(shù)字格式的部分已經(jīng)介紹過了，但是 沒有實際看一眼終究是不能有一個直觀的認(rèn)識，那在本文的***，我們就來看一個二進(jìn)制浮點數(shù)的在計算機(jī)中真實的樣子。

0100000001000111101101101101001001001000010101110011000100100011

這是一個64位的二進(jìn)制數(shù)。如果把它作為一個雙精度浮點數(shù)，那么它的各部分都分別表示了什么呢？

按照上文介紹浮點數(shù)的部分，我們可以將它分成如下幾部分：

符號：0

指數(shù)部分：10000000100（二進(jìn)制，可以轉(zhuǎn)換為十進(jìn)制的1028）

尾數(shù)部分：0111101101101101001001001000010101110011000100100011

因此，將它轉(zhuǎn)換為一個用二進(jìn)制表示的小數(shù)，則是：

(-1)^0 * 1.0111101101101101001001001000010101110011000100100011  x 2^(1028-1023)

= 1.0111101101101101001001001000010101110011000100100011  x 2^5

= 101111.01101101101001001001000010101110011000100100011

如果各位讀者觀察足夠仔細(xì)的話，是否發(fā)現(xiàn)了有趣的一點呢？那就是在這個在計算機(jī)中用來表示雙精度浮點數(shù)的64位數(shù)中，尾數(shù)部分的幾位數(shù)字是：0111101101101101001001001000010101110011000100100011

但是經(jīng)過從計算機(jī)中的形式轉(zhuǎn)化成人類使用二進(jìn)制表示小數(shù)的形式之后，數(shù)字卻變成了1.0111101101101101001001001000010101110011000100100011x 2^5，小數(shù)點之前為什么會多出了一個1呢？

這是因為在尾數(shù)部分，為了將表現(xiàn)形式多樣的浮點數(shù)統(tǒng)一為同一種表示方式而規(guī)定要將小數(shù)點前的值固定為1。由于小數(shù)點前的數(shù)永遠(yuǎn)是1，因此為了節(jié)省一個數(shù)據(jù)位，這個1在計算機(jī)中并不需要被保存。

那么應(yīng)該如何保證一個二進(jìn)制小數(shù)的小數(shù)點前的值是1呢？這就需要對二進(jìn)制小數(shù)進(jìn)行邏輯移位了，通過左移或右移若干次后，將整數(shù)部分變?yōu)?。例如上文中的這個二進(jìn)制小數(shù)：1110.1101，我們就來試試如何把它變成計算機(jī)可以識別的浮點數(shù)的尾數(shù)吧。

1110.1101（原始數(shù)據(jù)）——>0001.1101101（通過右移將整數(shù)部分變?yōu)?）—— >0001.11011010000000000000....（拓展位數(shù)，使之符合數(shù)字格式的規(guī)定）—— >11011010000000000000....（去掉整數(shù)部分，僅保留小數(shù)部分）

好了，到此關(guān)于C#或者計算機(jī)中的小數(shù)計算就寫得差不多了。歡迎各位交流。