深入理解CPU的分支預測(Branch Prediction)模型
說明: 本文以stackoverflow上Why is it faster to process a sorted array than an unsorted array?為原型,翻譯了問題和高票回答并加入了大量補充說明,方便讀者理解。
背景
先來看段c++代碼,我們用256的模數(shù)隨機填充一個固定大小的大數(shù)組,然后對數(shù)組的一半元素求和:
- #include <algorithm>
- #include <ctime>
- #include <iostream>
- int main()
- {
- // 隨機產生整數(shù),用分區(qū)函數(shù)填充,以避免出現(xiàn)分桶不均
- const unsigned arraySize = 32768;
- int data[arraySize];
- for (unsigned c = 0; c < arraySize; ++c)
- data[c] = std::rand() % 256;
- // !!! 排序后下面的Loop運行將更快
- std::sort(data, data + arraySize);
- // 測試部分
- clock_t start = clock();
- long long sum = 0;
- for (unsigned i = 0; i < 100000; ++i)
- {
- // 主要計算部分,選一半元素參與計算
- for (unsigned c = 0; c < arraySize; ++c)
- {
- if (data[c] >= 128)
- sum += data[c];
- }
- }
- double elapsedTime = static_cast<double>(clock() - start) / CLOCKS_PER_SEC;
- std::cout << elapsedTime << std::endl;
- std::cout << "sum = " << sum << std::endl;
- }
編譯并運行:
- g++ branch_prediction.cpp
- ./a.out
在我的macbook air上運行結果:
- # 1. 取消std::sort(data, data + arraySize);的注釋,即先排序后計算
- 10.218
- sum = 312426300000
- # 2. 注釋掉std::sort(data, data + arraySize);即不排序,直接計算
- 29.6809
- sum = 312426300000
由此可見,先排序后計算,運行效率有進3倍的提高。
為保證結論的可靠性, 我們再用java來測一遍:
- import java.util.Arrays;
- import java.util.Random;
- public class Main
- {
- public static void main(String[] args)
- {
- // Generate data
- int arraySize = 32768;
- int data[] = new int[arraySize];
- Random rnd = new Random(0);
- for (int c = 0; c < arraySize; ++c)
- data[c] = rnd.nextInt() % 256;
- // !!! With this, the next loop runs faster
- Arrays.sort(data);
- // Test
- long start = System.nanoTime();
- long sum = 0;
- for (int i = 0; i < 100000; ++i)
- {
- // Primary loop
- for (int c = 0; c < arraySize; ++c)
- {
- if (data[c] >= 128)
- sum += data[c];
- }
- }
- System.out.println((System.nanoTime() - start) / 1000000000.0);
- System.out.println("sum = " + sum);
- }
- }
在intellij idea中運行結果:
- # 1. 先排序后計算
- 5.549553
- sum = 155184200000
- # 2. 不排序直接結算
- 15.527867
- sum = 155184200000
也有三倍左右的差距。且java版要比c++版整體快近乎1倍?這應該是編譯時用了默認選項,gcc優(yōu)化不夠的原因,后續(xù)再調查這個問題。
問題的提出
以上代碼在數(shù)組填充時已經加入了分區(qū)函數(shù),充分保證填充值的隨機性,計算時也是按一半的元素來求和,所以不存在特例情況。而且,計算也完全不涉及到數(shù)據(jù)的有序性,即數(shù)組是否有序理論上對計算不會產生任何作用。在這樣的前提下,為什么排序后的數(shù)組要比未排序數(shù)組運行快3倍以上?
分析
想象一個鐵路分叉道口。
為了論證此問題,讓我們回到19世紀,那個遠距離無線通信還未普及的年代。你是鐵路交叉口的扳道工。當聽到火車快來了的時候,你無法猜測它應該朝哪個方向走。于是你叫停了火車,上前去問火車司機該朝哪個方向走,以便你能正確地切換鐵軌。
要知道,火車是非常龐大的,切急速行駛時有巨大的慣性。為了完成上述停車-問詢-切軌的一系列動作,火車需耗費大量時間減速,停車,重新開啟。
既然上述過車非常耗時,那是否有更好的方法?當然有!當火車即將行駛過來前,你可以猜測火車該朝哪個方向走。
- 如果猜對了,它直接通過,繼續(xù)前行。
- 如果猜錯了,車頭將停止,倒回去,你將鐵軌扳至反方向,火車重新啟動,駛過道口。
如果你不幸每次都猜錯了,那么火車將耗費大量時間停車-倒回-重啟。如果你很幸運,每次都猜對了呢?火車將從不停車,持續(xù)前行!
上述比喻可應用于處理器級別的分支跳轉指令里:
原程序:
- if (data[c] >= 128)
- sum += data[c];
匯編碼:
- cmp edx, 128
- jl SHORT $LN3@main
- add rbx, rdx
- $LN3@main:
讓我們回到文章開頭的問題。現(xiàn)在假設你是處理器,當看到上述分支時,當你并不能決定該如何往下走,該如何做?只能暫停運行,等待之前的指令運行結束。然后才能繼續(xù)沿著正確地路徑往下走。
要知道,現(xiàn)代編譯器是非常復雜的,運行時有著非常長的pipelines, 減速和熱啟動將耗費巨量的時間。
那么,有沒有好的辦法可以節(jié)省這些狀態(tài)切換的時間呢?你可以猜測分支的下一步走向!
如果猜錯了,處理器要flush掉pipelines, 回滾到之前的分支,然后重新熱啟動,選擇另一條路徑。
如果猜對了,處理器不需要暫停,繼續(xù)往下執(zhí)行。
如果每次都猜錯了,處理器將耗費大量時間在停止-回滾-熱啟動這一周期性過程里。如果僥幸每次都猜對了,那么處理器將從不暫停,一直運行至結束。
上述過程就是分支預測(branch prediction)。雖然在現(xiàn)實的道口鐵軌切換中,可以通過一個小旗子作為信號來判斷火車的走向,但是處理器卻無法像火車那樣去預知分支的走向--除非最后一次指令運行完畢。
那么處理器該采用怎樣的策略來用最小的次數(shù)來盡量猜對指令分支的下一步走向呢?答案就是分析歷史運行記錄: 如果火車過去90%的時間都是走左邊的鐵軌,本次軌道切換,你就可以猜測方向為左,反之,則為右。如果在某個方向上走過了3次,接下來你也可以猜測火車將繼續(xù)在這個方向上運行...
換句話說,你試圖通過歷史記錄,識別出一種隱含的模式并嘗試在后續(xù)鐵道切換的抉擇中繼續(xù)應用它。這和處理器的分支預測原理或多或少有點相似。
大多數(shù)應用都具有狀態(tài)良好的(well-behaved)分支,所以現(xiàn)代化的分支預測器一般具有超過90%的命中率。但是面對無法預測的分支,且沒有識別出可應用的的模式時,分支預測器就無用武之地了。
關于分支預測期,可參考維基百科相關詞條"Branch predictor" article on Wikipedia..
文首導致非排序數(shù)組相加耗時顯著增加的罪魁禍首便是if邏輯:
- if (data[c] >= 128)
- sum += data[c];
注意到data數(shù)組里的元素是按照0-255的值被均勻存儲的(類似均勻的分桶)。數(shù)組data有序時,前面一半元素的迭代將不會進入if-statement, 超過一半時,元素迭代將全部進入if-statement.
這樣的持續(xù)朝同一個方向切換的迭代對分支預測器來說是非常友好的,前半部分元素迭代完之后,后續(xù)迭代分支預測器對分支方向的切換預測將全部正確。
簡單地分析一下:有序數(shù)組的分支預測流程:
- T = 分支命中
- N = 分支沒有命中
- data[] = 0, 1, 2, 3, 4, ... 126, 127, 128, 129, 130, ... 250, 251, 252, ...
- branch = N N N N N ... N N T T T ... T T T ...
- = NNNNNNNNNNNN ... NNNNNNNTTTTTTTTT ... TTTTTTTTTT (非常容易預測)
無序數(shù)組的分支預測流程:
- data[] = 226, 185, 125, 158, 198, 144, 217, 79, 202, 118, 14, 150, 177, 182, 133, ...
- branch = T, T, N, T, T, T, T, N, T, N, N, T, T, T, N ...
- = TTNTTTTNTNNTTTN ... (完全隨機--無法預測)
在本例中,由于data數(shù)組元素填充的特殊性,決定了分支預測器在未排序數(shù)組迭代過程中將有50%的錯誤命中率,因而執(zhí)行完整個sum操作將會耗時更多。
優(yōu)化
利用位運算取消分支跳轉。基本知識:
- |x| >> 31 = 0 # 非負數(shù)右移31為一定為0
- ~(|x| >> 31) = -1 # 0取反為-1
- -|x| >> 31 = -1 # 負數(shù)右移31為一定為0xffff = -1
- ~(-|x| >> 31) = 0 # -1取反為0
- -1 = 0xffff
- -1 & x = x # 以-1為mask和任何數(shù)求與,值不變
故分支判斷可優(yōu)化為:
- int t = (data[c] - 128) >> 31; # statement 1
- sum += ~t & data[c]; # statement 2
分析:
- data[c] < 128, 則statement 1值為: 0xffff = -1, statement 2等號右側值為: 0 & data[c] == 0;
- data[c] >= 128, 則statement 1值為: 0, statement 2等號右側值為: ~0 & data[c] == -1 & data[c] == 0xffff & data[c] == data[c];
故上述位運算實現(xiàn)的sum邏輯完全等價于if-statement, 更多的位運算hack操作請參見bithacks.
若想避免移位操作,可以使用如下方式:
- int t=-((data[c]>=128)); # generate the mask
- sum += ~t & data[c]; # bitwise AND
結論
- 使用分支預測: 是否排序嚴重影響performance
- 使用bithack: 是否排序對performance無顯著影響
這個例子告訴給我們啟示: 在大規(guī)模循環(huán)邏輯中要盡量避免數(shù)據(jù)強依賴的分支(data-dependent branching).
補充知識
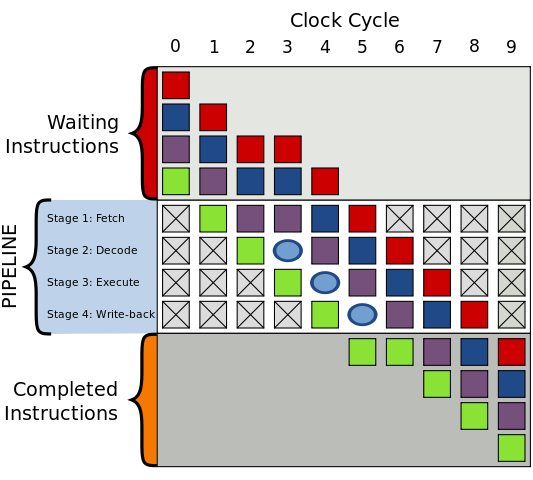
Pipeline
先簡單說明一下CPU的instruction pipeline(指令流水線),以下簡稱pipeline。 Pipieline假設程序運行時有一連串指令要被運行,將程序運行劃分成幾個階段,按照一定的順序并行處理之,這樣便能夠加速指令的通過速度。
絕大多數(shù)pipeline都由時鐘頻率(clock)控制,在數(shù)字電路中,clock控制邏輯門電路(logical cicuit)和觸發(fā)器(trigger), 當受到時鐘頻率觸發(fā)時,觸發(fā)器得到新的數(shù)值,并且邏輯門需要一段時間來解析出新的數(shù)值,而當受到下一個時鐘頻率觸發(fā)時觸發(fā)器又得到新的數(shù)值,以此類推。
而借由邏輯門分散成很多小區(qū)塊,再讓觸發(fā)器鏈接這些小區(qū)塊組,使邏輯門輸出正確數(shù)值的時間延遲得以減少,這樣一來就可以減少指令運行所需要的周期。 這對應Pipeline中的各個stages。
一般的pipeline有四個執(zhí)行階段(execuate stage): 讀取指令(Fetch) -> 指令解碼(Decode) -> 運行指令(Execute) -> 寫回運行結果(Write-back).
分支預測器
分支預測器是一種數(shù)字電路,在分支指令執(zhí)行前,猜測哪一個分支會被執(zhí)行,能顯著提高pipelines的性能。
條件分支通常有兩路后續(xù)執(zhí)行分支,not token時,跳過接下來的JMP指令,繼續(xù)執(zhí)行, token時,執(zhí)行JMP指令,跳轉到另一塊程序內存去執(zhí)行。
為了說明這個問題,我們先考慮如下問題。
沒有分支預測器會怎樣?
加入沒有分支預測器,處理器會等待分支指令通過了pipeline的執(zhí)行階段(execuate stage)才能把下一條指令送入pipeline的fetch stage。
這會造成流水線停頓(stalled)或流水線冒泡(bubbling)或流水線打嗝(hiccup),即在流水線中生成一個沒有實效的氣泡, 如下圖所示:
圖中一個氣泡在編號為3的始終頻率中產生,指令運行被延遲。
Stream hiccup現(xiàn)象在早期的RISC體系結構處理器中常見。
有分支預測期的pipeline
我們來看分支預測器在條件分支跳轉中的應用。條件分支通常有兩路后續(xù)執(zhí)行分支,not token時,跳過接下來的JMP指令,繼續(xù)執(zhí)行, token時,執(zhí)行JMP指令,跳轉到另一塊程序內存去執(zhí)行。
加入分支預測器后,為避免pipeline停頓(stream stalled),其會猜測兩路分支哪一路最有可能執(zhí)行,然后投機執(zhí)行,如果猜錯,則流水線中投機執(zhí)行中間結果全部拋棄,重新獲取正確分支路線上的指令執(zhí)行。可見,錯誤的預測會導致程序執(zhí)行的延遲。
由前面可知,Pipeline執(zhí)行主要涉及Fetch, Decode, Execute, Write-back幾個stages, 分支預測失敗會浪費Write-back之前的流水線級數(shù)。現(xiàn)代CPU流水線級數(shù)非常長,分支預測失敗可能會損失20個左右的時鐘周期,因此對于復雜的流水線,好的分支預測器非常重要。
常見的分支預測器
- 靜態(tài)分支預測器
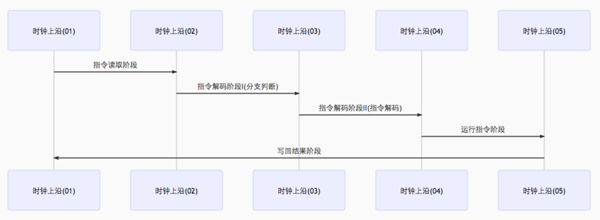
靜態(tài)分支預測器有兩個解碼周期,分別評價分支,解碼。即在分支指令執(zhí)行前共經歷三個時鐘周期。詳情見圖:
- 雙模態(tài)預測器(bimodal predictor)
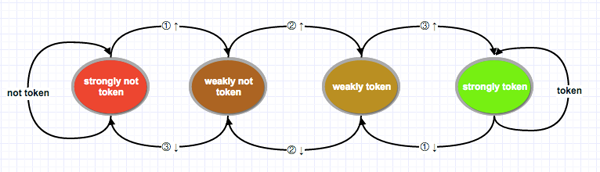
也叫飽和計數(shù)器,是一個四狀態(tài)狀態(tài)機. 四個狀態(tài)對應兩個選擇: token, not token, 每個選擇有兩個狀態(tài)區(qū)分強弱:strongly,weakly。分別是Strongly not taken,Weakly not taken, Weakly taken, Strongly taken。
狀態(tài)機工作原理圖如下:
圖左邊兩個狀態(tài)為不采納(not token),右邊兩個為采納(token)。由not token到token中間有兩個漸變狀態(tài)。由紅色到綠色翻轉需要連續(xù)兩次分支選擇。
技術實現(xiàn)上可用兩個二進制位來表示,00, 01, 10, 11分別對應strongly not token, weakly not token, weakly token, strongly token。 一個判斷兩個分支預測規(guī)則是否改變的簡單方法便是判斷這個二級制狀態(tài)高位是否跳變。高位從0變?yōu)?, 強狀態(tài)發(fā)生翻轉,則下一個分支指令預測從not token變?yōu)閠oken,反之亦然。
據(jù)評測,雙模態(tài)預測器的正確率可達到93.5%。預測期一般在分支指令解碼前起作用。
其它常見分支預測器如兩級自適應預測器,局部/全局分支預測器,融合分支預測器,Agree預測期,神經分支預測器等。