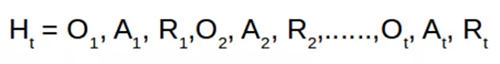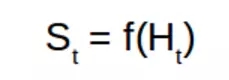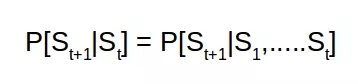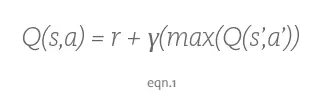從強化學習基本概念到Q學習的實現,打造自己的迷宮智能體
近年以來,強化學習在人工智能所充當的角色越來越重要了,很多研究機構和大學都將強化學習與深度學習相結合打造高性能的系統。因此,本文注重描述強化學習的基本概念與實現,希望能為讀者介紹這一機器學習分支的巨大魅力。
強化學習其實也是機器學習的一個分支,但是它與我們常見監督學習和無監督學習又不太一樣。強化學習旨在選擇***決策,它講究在一系列的情景之下,通過多步恰當的決策來達到一個目標,是一種序列多步決策的問題。該學習算法能幫助我們公式化表達生物體以獎勵為動機(reward-motivated)的行為。比如說,讓一個孩子坐下來安靜地為考試而復習是十分困難的,但如果你在他每次學完一章時獎勵一塊巧克力,那么他就會明白只有保持學習才能獲得獎勵,因此也就有動力復習備考。而現在,如果這個孩子在備考時沒有明確的方法,他可能會花大量時間學習一個章節而不能及時完成課程大綱。所以我們需要小孩有效率地學,因此如果小孩在一小時內完成某章節,那么就獎勵大塊巧克力,而超過 1 小時那就只獎勵小塊巧克力。現在他不僅會學習,同時大腦會思考設計出更快完成章節學習的方法。
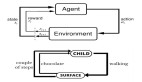
在這個例子中,孩子就是代表著訓練實體(Agent :與環境交互的對象)。獎勵系統和考試就代表著環境(Environment)。而章節就可以類比為強化學習的狀態(States)。所以孩子們就需要決定哪些章節更重要(即計算每一個章節的值),這也就是價值函數(Value-Function)所做的事。并且小孩每次從一個狀態到另一個狀態就能收到獎勵,而他隨時間完成章節的方式就是策略(Policy)。
強化學習和其他機器學習范式有什么不同:
- 沒有大量標注數據進行監督,所以也就不能由樣本數據告訴系統什么是最可能的動作,訓練主體只能從每一步動作得出獎勵。因此系統是不能立即得到標記的,而只能得到一個反饋,也可以說強化學習是一種標記延遲的監督學習。
- 時間序列的重要性,強化學習不像其他接受隨機輸入的學習方法,其更注重序列型數據,并且下一步的輸入經常依賴于前一狀態的輸入。
- 延遲獎勵的概念,系統可能不會在每步動作上都獲得獎勵,而只有當完成整個任務時才會獲得獎勵。
- 訓練實體的動作影響下一個輸入。如你可以選擇向左走或向右走,那么當選擇的方向不同時,下一個時間步的輸入也會不同。即選擇不同的動作進入不同的狀態后,當前可選的動作又不一樣。
總的來說,強化學習的目標就是要尋找一個能使得我們獲得***累積獎賞的策略。因此,強化學習實際上和我們人類與環境的交互方式類似,是一套非常通用的框架,可以用來解決各種各樣的人工智能的問題。
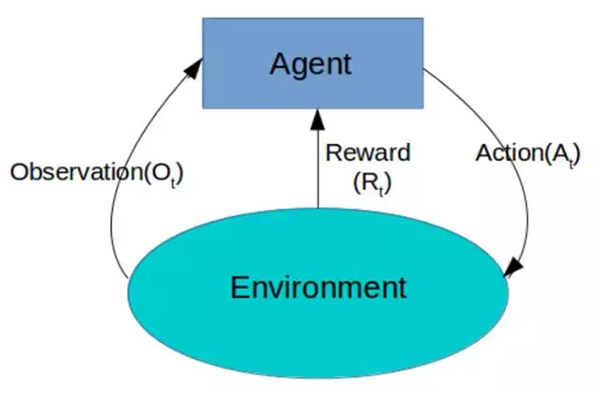
如上所示,在任何時間步(t),訓練實體會得到一個環境的觀察值(實例)。然后它會從所有可行動作中采取一種,并獲得環境的獎勵和下一個觀察值。所以我們需要為訓練實體提供算法,其所作出的決策應該是以***化提升結束時的全部獎勵為目的。
一、歷史與狀態
歷史(History)是描述在環境和訓練實體之間發生的所有事件的變量集合。
訓練實體必須將歷史映射到一個確切的動作中。對于環境,其必須將歷史映射到需要發送的下一組觀察值。因此,訓練實體必須持續保持并儲存大量的信息,這將占用大量的儲存空間和處理時間。
所以,我們想創建歷史的抽象表征,它可以儲存足夠的信息以便我們可以選擇下一步動作,這也就是狀態的概念。所以基本上系統的輸出就取決于我們怎樣定義狀態。
在上式中,S 表征狀態、f 表征一種能對時間步「t」的歷史求和的函數。
上述表達式中,前一個代表訓練實體的內部表征,其可以對歷史求和并允許在以后采取動作。而后一個代表環境的內部表征,其允許發送下一個觀察值。
1. 馬爾可夫狀態(Markov State)
馬爾可夫狀態使用抽象形式儲存過去所有的信息。所以如果訓練實體預測未來的動作,其并不會使用全部的歷史,而是使用馬爾可夫狀態。本質上來說,馬爾可夫狀態儲存的信息并不比歷史少。
所以在給定狀態 St 的情況下求未來狀態 St+1 的概率和給定前面所有狀態求 St+1 的概率相同。這是因為狀態 St 已經將前面所有狀態的信息都嵌入了其中。
2. 序列的游戲
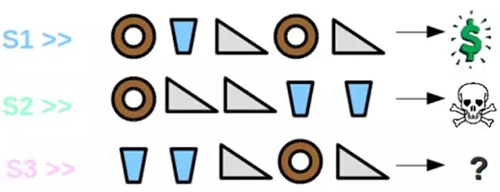
現在假設有個游戲發生在餐廳里,餐廳提供三種食物:甜甜圈、飲料和三明治。現在顧客要求服務員帶五樣食品,且服務員會按順序依次提供這五樣食品。如果顧客喜歡這些食物的順序,那么服務員將得到獎勵,否則就會得到懲罰。現在服務員***次提供食物的順序如 S1 所示,他得到了獎勵。
然而,當下一次服務員又以另一個順序帶來五份食品(S2)時,他得到了懲罰。那么現在第三個序列 S3 的輸出是什么,獎勵還是懲罰?
這里的解決方案取決于先前狀態的定義。如果說狀態的定義僅僅只是采用食物序列***三項的順序,那么根據 S1 ***三項的結果,S3 序列能獲得獎勵。然而如果根據每個食物出現的數量來定義,那么 S3 最有可能得到懲罰,因為 S2 和 S3 每一份食物的數量都相同。所以本質上系統的輸出是依賴于狀態的定義。
二、環境
如果你在電腦上玩自己編寫的象棋,那么你就很清楚計算機是如何分析怎樣下棋。所以基本上你知道在給定的行動下電腦確定的是哪一步棋。這是一種完全可觀察的環境(Fully Observable Environment)。
現在如果你在玩由其他人編寫的象棋游戲,你并不知道電腦下一步會怎么下。所以現在你能做的就是在下一步棋后觀察電腦的下棋。這是一種部分可觀察環境(Partially Observable Environment)。在這種情況下,你能做的就是預測游戲的內部動態,并期望能對其內部狀態能有一個足夠好的預測。
另外,根據周志華的《機器學習》,我們需注意「機器」與「環境」的界限。例如在種西瓜任務中,環境是西瓜生長的自然世界;在下棋對弈中,環境是棋盤與對手;在機器人控制中,環境是機器人的軀體與物理世界。總之,在環境中狀態的轉移、獎賞的返回是不受機器控制的,機器只能通過選擇要執行的動作來影響環境,也只能通過觀察轉移后的狀態和返回的獎賞來感知環境。
***總結一下強化學習的概念,強化學習的輸入 是:
- 狀態 (States) = 環境,例如迷宮的每一格就是一個狀態
- 動作 (Actions) = 在每個狀態下,有什么行動是容許的
- 獎勵 (Rewards) = 進入每個狀態時,能帶來正面或負面的價值 (utility)
而輸出就是:
- 策略 (Policy) = 在每個狀態下,你會選擇哪個行動?
如上圖所示,強化學習的思想主要:即訓練實體 (Agent) 不斷地采取動作 (action), 之后轉到下一個狀態 (State), 并且獲得一個獎勵 (reward), 從而進一步更新訓練實體。
在了解了強化學習的基本概念后,我們就可以進一步理解 Q 學習(Q-Learning)的原理和實現。
下面我們將從迷宮尋寶游戲開始了解 Q 學習的基本概念。該游戲規則如下:
該游戲從一個給定的位置開始,即初始狀態(starting state)。在每一個狀態下訓練實體都可以保留原地或選擇向上、下、左、右移動,但不能穿越迷宮的邊界。每個動作都將使得訓練實體進入不同的單元格(即不同的狀態)。現在在某個單元格有一個寶箱(即目標狀態)。此外,迷宮的某些位置/狀態有蛇。因此訓練實體的目標就是通過尋找一條沒有蛇的路徑從起始狀態走到目標狀態。
現在當我們在網格中(即環境中)放置一個訓練實體,它首先會開始探索。它最開始不知道蛇是什么,也不知道什么是寶箱或寶箱在哪。所以我們需要給定訓練主體蛇和寶箱的概念,并在每一步動作后給予一定的獎勵。對于每一塊有蛇的單元格(狀態),我們給予-10 的獎勵,而對于寶藏,我們給予+10 的獎勵。現在我們希望訓練實體盡快完成任務(采取最短路徑),因此我們給予其他狀態-1 的獎勵。***我們給定訓練實體的目標就是***化***累積得分。隨著訓練實體的探索,它會知道蛇是有害的,寶藏是有益的,并且它需要盡可能快地得到寶箱。上圖中「-」就表示從起始狀態到目標狀態最短的路徑。
Q 學習(Q-Learning)就嘗試在給定狀態下學習當前值,并采取特定的動作。
現在我們設計一張表格,其中每行是訓練實體的狀態,而每列是訓練實體可能采取的動作。所以上例有 16×5 種可能的狀態-行動對,其中每種狀態都是迷宮中的一個單元格。
首先我們初始化矩陣(上文所述的 16×5 表格)為零矩陣,然后根據不同動作所獲得的獎勵更新矩陣的元素。當然,更新該矩陣的方法為計算貝爾曼方程(Bellman Equation):
「S」代表當前狀態,「a」代表訓練實體在當前狀態下所采取的動作,「S'」代表采取該動作所產生的狀態,「r'」是采取該動作所得到的獎勵。貼現系數(discount factor)「γ」決定了訓練實體對未來獎勵的重視程度,γ越大,訓練實體就會越重視以往經驗,而γ越小,訓練實體只重視眼前的利益。如果說訓練實體向遠離目標狀態的狀態運動,而該狀態遇到蛇的概率減少,那么實時獎勵將減少,未來獎勵將增加,訓練實體更注重未來的獎勵。
我們將每次迭代(訓練主體的嘗試動作)作為一個 episode。對于每一次 episode,訓練主體將嘗試到達目標狀態,并且對于每一次動作,Q 矩陣元素都會進行一次更新。
現在讓我們了解一下 Q 矩陣是如何計算的(為了更簡潔,我們采用更小的 2×2 迷宮):
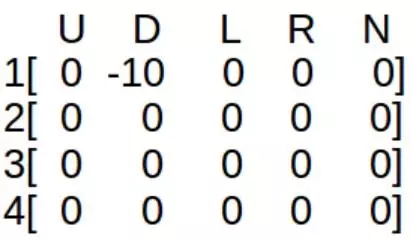
Q 矩陣的初始狀態如下(每行代表一個狀態,每列代表一個動作):
U—向上走, D—向下走, L—向左走, R—向右走
獎勵矩陣如下所示:
其中 E 代表空值(NULL,訓練主體不能采取該動作)
算法:
- 初始化 Q 矩陣為零矩陣,設定「γ」值,完成獎勵矩陣。
- 對于每一 episode,選擇一個隨機起始狀態(在這個案例中,我們嚴格限制起始狀態為-1)。
- 在當前狀態(S)的所有可能動作中選擇一個。
- 作為該動作(a)的結果,訓練主體移往下一個狀態(S')。
- 對于狀態(S')產生的所有可能動作,選擇 Q 值***的動作。
- 使用貝爾曼方程(Bellman Equation)更新 Q 矩陣。
- 將下一個狀態設置為當前狀態。
- 如果到達目標狀態,結束算法。
我們可以從以下一段偽代碼進一步理解:
現在假設訓練主體從狀態 1 開始,其可以采取動作 D 或 R。如果采取了動作 D,那么訓練主體到達狀態 3(蛇),并可以采取動作 U 或 R。現在取值γ = 0.8,那么方程有:
- Q(1,D) = R(1,D) + γ*[max(Q(3,U) & Q(3,R))]
- Q(1,D) = -10 + 0.8*0 = -10
其中,因為 Q 矩陣還沒有更新,max(Q(3,U) & Q(3,R)) = 0。設定設定踩上蛇的獎勵為-10。現在新的 Q 矩陣的值就如下所示:
現在,狀態 3 為當前狀態,從狀態 3 采取了動作 R。訓練主體就到達狀態 4,并其可以采取動作 U 或 L。
- Q(3,R) = R(3,R) + 0.8*[max(Q(4,U) & Q(4,L))]
- Q(3,R) = 10 + 0.8*0 = 10
再一次更新 Q 矩陣的值:
所以,現在訓練主體到達目標狀態 4。接下來終止該進程,并進行更多的訓練直到訓練主體理解了所有狀態和動作,且所有的 Q 矩陣元素成為常數。這也就意味為訓練主體已經嘗試了所有的狀態-動作對。
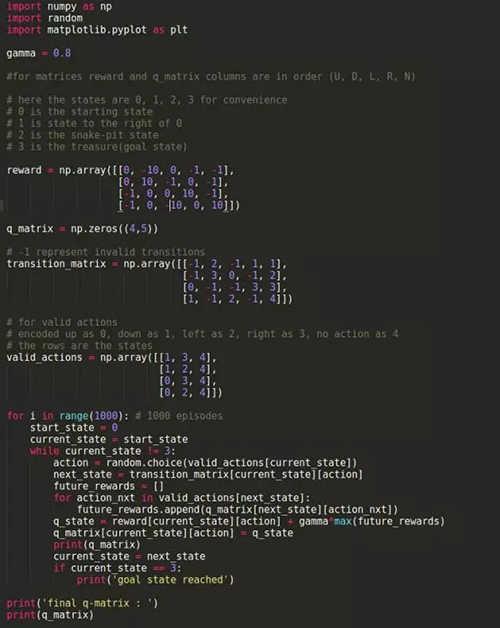
這一過程的 Python 實現:
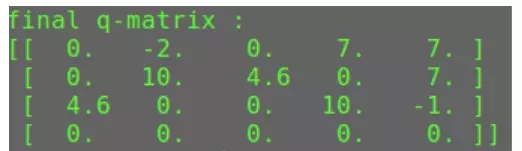
*** Q 矩陣的輸出:
原文:
https://medium.com/becoming-human/the-very-basics-of-reinforcement-learning-154f28a79071
【本文是51CTO專欄機構機器之心的原創譯文,微信公眾號“機器之心( id: almosthuman2014)”】