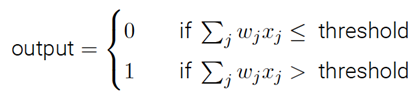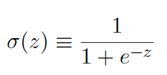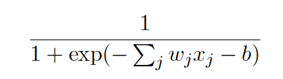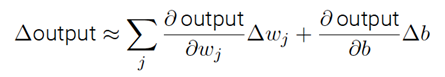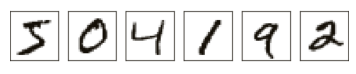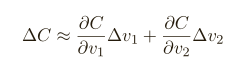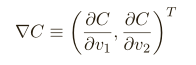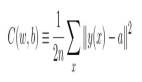理解深度學習的鑰匙 –啟蒙篇
神經網絡是有史以來發明的最優美的編程范式之⼀。在傳統的編程⽅法中,我們告訴計算機做什么,把⼤問題分成許多小的、精確定義的任務,計算機可以很容易地執行。相比之下,在神經網絡中,我們不告訴計算機如何解決我們的問題。相反,它從觀測數據中學習,找出它自己的解決問題的辦法。
從數據中自動學習,聽上去很有前途。然而,直到 2006 年,除了用于一些特殊的問題,我們仍然不知道如何訓練神經⽹絡去超越傳統的⽅法。2006 年,被稱為 “深度神經網絡” 的學習技術的發現引起了變化。這些技術現在被稱為 “深度學習”。它們已被進⼀步發展,今天深度神經網絡和深度學習在計算機視覺、語音識別、自然語言處理等許多重要問題上都取得了顯著的性能。
筆者從一年前接觸深度學習,驚嘆于AlphaGo所取得的成績,任何雄心于建模領域的數據管理者,不管你現在是否還在自己建模,或者正領導著一只團隊向前走,都有必要去理解一下深度學習到底是什么,如果你還敢說自己是數據方面的專業人士的話,但任何媒體上的關于深度學習的介紹,其深度都是及其有限的,幾乎可以說,對一個數據管理者的學識提升沒有什么幫助。
即使你已經知道了TensorFlow這類引擎,甚至已經安排開始安裝這里引擎,依樣畫葫蘆的去完成一個深度學習的過程,也僅僅是術上的一個追求,如果你想要了解今后⼏年都不會過時的原理,那么只是學習些熱⻔的程序庫是不夠的,你需要領悟讓神經⽹絡⼯作的原理。技術來來去去,但原理是永恒的。
筆者曾經寫過一篇《我如何理解深度學習?》的微信公眾號文章,那個是及其簡單的一個淺層次理解,對于構建一個真正的深度學習神經網絡沒有指導作用,因為神經網絡本質上屬于機器學習的一類,其難點在于如何構建一個可用的多層神經網絡,而不是說深度神經網絡是個什么東西,那個其實沒有啥秘密可言。
牛逼的深度學習專家肯定是網絡架構、參數調優的高手,而不是簡單的反復說深度學習是啥東西,筆者一直沒勇氣去深入的理解神經網絡最核心的東西-參數,導致我一直游離在這門實踐學科之外,這次斗膽看了些書,網上找了些文章,多了點理解,對于神經網絡的參數有了一些基本的概念,這些都是打造一個深度學習價值網絡的基礎。
團隊的同事最近自己在研究深度學習,說出來的結果比SVM差很多,我想,肯定是不懂參數和調試的方法吧。
筆者數學并不好,極大降低了學習的效率,我想很多人應該跟我一樣,也不可能再有機會去重讀一次高等數學,這是一個數學上的殘疾人理解的深度學習,我能做的,就是當個知識的搬運工,用最通俗易懂的方式闡述我所理解的東西,讓很多看似深奧的東西盡量平民化一點,從“道”的角度去理解一個深度網絡,也許,還能有些生活的感悟呢。
由于理解深度學習的前提是理解神經網絡,因此,筆者會試著寫三篇文章,分別是啟蒙篇,參數篇及總結篇,深入淺出的給出我的理解,所有的資料都來自網上電子書《Neural Networks and Deep Learning》,這本書寫得實在太好了,我只是剪輯了下,吸出了其中的精髓,希望你堅持看完。
Part 1
感知器
這一節你能理解什么是感知器以及為什么要用S型(邏輯)感知器。
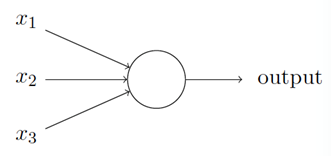
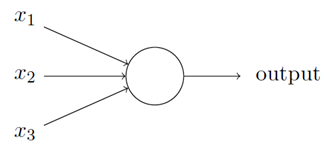
什么是神經網絡?一開始,我將解釋⼀種被稱為“感知器”的人工神經元,感知器是如何⼯作的呢?⼀個感知器接受⼏個⼆進制輸⼊,x1; x2;x3,并產⽣⼀個⼆進制輸出:
⽰例中的感知器有三個輸⼊,x1; x2; x3。通常可以有更多或更少輸⼊。Rosenblatt 提議⼀個簡單的規則來計算輸出。他引⼊權重,w1;w2……,表示相應輸⼊對于輸出重要性的實數。神經元的輸出,0 或者1,則由分配權重后的總和Σj wjxj ⼩于或者⼤于⼀些閾值決定。和權重⼀樣,閾值是⼀個實數,⼀個神經元的參數,⽤更精確的代數形式:
這是基本的數學模型。你可以將感知器看作依據權重來作出決定的設備。讓我舉個例⼦。這不是⾮常真實的例⼦,但是容易理解,⽽且很快我們會有根多實際的例⼦。假設這個周末就要來了,你聽說你所在的城市有個奶酪節,你喜歡奶酪,正試著決定是否去參加。你也許會通過給三個因素設置權重來作出決定:
1. 天氣好嗎?
2. 你的男朋友或者⼥朋友會不會陪你去?
3. 這個節⽇舉辦的地點是否靠近交通站點?(你沒有⻋)
你可以把這三個因素對應地⽤⼆進制變量x1; x2 和x3 來表⽰。例如,如果天⽓好,我們把x1 = 1,如果不好,x1 = 0。類似地,如果你的男朋友或⼥朋友同去,x2 = 1,否則x2 = 0。x3也類似地表⽰交通情況。
現在,假設你是個嗜好奶酪的吃貨,以⾄于即使你的男朋友或⼥朋友不感興趣,也不管路有多難⾛都樂意去。但是也許你確實厭惡糟糕的天⽓,⽽且如果天⽓太糟你也沒法出⻔。你可以使⽤感知器來給這種決策建⽴數學模型。⼀種⽅式是給天⽓權重選擇為w1 = 6 ,其它條件為w2 = 2 和w3 = 2。w1 被賦予更⼤的值,表⽰天⽓對你很重要,⽐你的男朋友或⼥朋友陪你,或者最近的交通站重要的多。最后,假設你將感知器的閾值設為5。這樣,感知器實現了期望的決策模型,只要天⽓好就輸出1,天⽓不好則為0。對于你的男朋友或⼥朋友是否想去,或者附近是否有公共交通站,其輸出則沒有差別。隨著權重和閾值的變化,你可以得到不同的決策模型。例如,假設我們把閾值改為3 。那么感知器會按照天⽓好壞,或者結合交通情況和你男朋友或⼥朋友同⾏的意愿,來得出結果。換句話說,它變成了另⼀個不同的決策模型。降低閾值則表⽰你更愿意去。
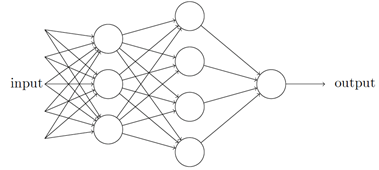
這個例⼦說明了⼀個感知器如何能權衡不同的依據來決策,這看上去也可以⼤致解釋⼀個感知器⽹絡能夠做出微妙的決定:
在這個⽹絡中,第⼀列感知器—— 我們稱其為第⼀層感知器—— 通過權衡輸⼊依據做出三個⾮常簡單的決定。那第⼆層的感知器呢?每⼀個都在權衡第⼀層的決策結果并做出決定。以這種⽅式,⼀個第⼆層中的感知器可以⽐第⼀層中的做出更復雜和抽象的決策。在第三層中的感知器甚⾄能進⾏更復雜的決策。以這種⽅式,⼀個多層的感知器⽹絡可以從事復雜巧妙的決策。
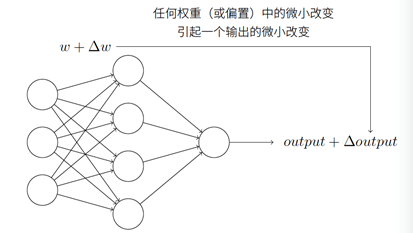
假設我們有⼀個感知器⽹絡,想要⽤它來解決⼀些問題。例如,⽹絡的輸⼊可以是⼀幅⼿寫數字的掃描圖像。我們想要⽹絡能學習權重和偏置,這樣⽹絡的輸出能正確分類這些數字。為了看清學習是怎樣⼯作的,假設我們把⽹絡中的權重(或者偏置)做些微⼩的改動,就像我們⻢上會看到的,這⼀屬性會讓學習變得可能,這⾥簡要⽰意我們想要的。
如果對權重(或者偏置)的微⼩的改動真的能夠僅僅引起輸出的微⼩變化,那我們可以利⽤這⼀事實來修改權重和偏置,讓我們的⽹絡能夠表現得像我們想要的那樣。例如,假設⽹絡錯誤地把⼀個“9”的圖像分類為“8”。我們能夠計算出怎么對權重和偏置做些⼩的改動,這樣⽹絡能夠接近于把圖像分類為“9”。然后我們要重復這個⼯作,反復改動權重和偏置來產⽣更好的輸出,這時⽹絡就在學習。
問題在于當我們的⽹絡包含感知器時這不會發⽣,實際上,⽹絡中單個感知器上⼀個權重或偏置的微⼩改動有時候會引起那個感知器的輸出完全翻轉,如0 變到1,那樣的翻轉可能接下來引起其余⽹絡的⾏為以極其復雜的⽅式完全改變。因此,雖然你的“9”可能被正確分類,⽹絡在其它圖像上的⾏為很可能以⼀些很難控制的⽅式被完全改變,這使得逐步修改權重和偏置來讓⽹絡接近期望⾏為變得困難,也許有其它聰明的⽅式來解決這個問題。但是這不是顯⽽易⻅地能讓⼀個感知器⽹絡去學習。
我們可以引⼊⼀種稱為S 型神經元的新的⼈⼯神經元來克服這個問題,S 型神經元和感知器類似,但是被修改為權重和偏置的微⼩改動只引起輸出的微⼩變化。這對于讓神經元⽹絡學習起來是很關鍵的。
我們⽤描繪感知器的相同⽅式來描繪S 型神經元:
正如⼀個感知器,S 型神經元有多個輸⼊,x1; x2; ……。但是這些輸⼊可以取0 和1 中的任意值,⽽不僅僅是0 或1。例如,0:638 是⼀個S 型神經元的有效輸⼊,同樣,S 型神經元對每個輸⼊有權重,w1;w2……,和⼀個總的偏置b。但是輸出不是0 或1。相反,它現在是σ (w x+b),這⾥σ被稱為S 型函數,有時被稱為邏輯函數,⽽這種新的神經元類型被稱為邏輯神經元,定義為:
把它們放在⼀起來更清楚地說明,⼀個具有輸⼊x1; x2;……,權重w1;w2; …..,和偏置b 的S型神經元的輸出是:
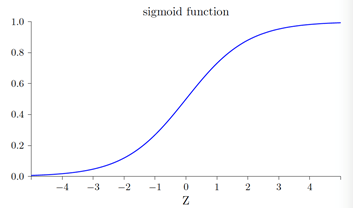
σ(z)圖形如下所示:
σ的平滑意味著權重和偏置的微⼩變化,即Δwj 和Δb,會從神經元產⽣⼀個微⼩的輸出變化Δoutput。實際上,微積分告訴我們Δoutput 可以很好地近似表⽰為:
上⾯全部⽤偏導數的表達式看上去很復雜,實際上它的意思⾮常簡單(這可是個好消息):Δoutput 是⼀個反映權重和偏置變化即Δwj 和Δb的線性函數。
Part 2
神經網絡的架構
這一節告訴你神經網絡長什么模樣?
下面這個⽹絡中最左邊的稱為輸⼊層,其中的神經元稱為輸⼊神經元,最右邊的,即輸出層包含有輸出神經元,在本例中,輸出層只有⼀個神經元,中間層,既然這層中的神經元既不是輸⼊也不是輸出,則被稱為隱藏層。
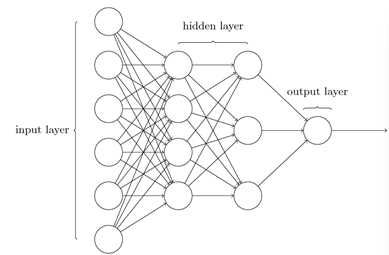
假設我們嘗試確定⼀張⼿寫數字的圖像上是否寫的是“9”,很⾃然地,我們可以將圖⽚像素的強度進⾏編碼作為輸⼊神經元來設計⽹絡,如果圖像是⼀個64 * 64 的灰度圖像,那么我們會需要4096 = 64 * 64 個輸⼊神經元,每個強度取0 和1 之間合適的值。輸出層只需要包含⼀個神經元,當輸出值⼩于0.5 時表⽰“輸⼊圖像不是⼀個9”,⼤于0.5 的值表⽰“輸⼊圖像是⼀個9”。
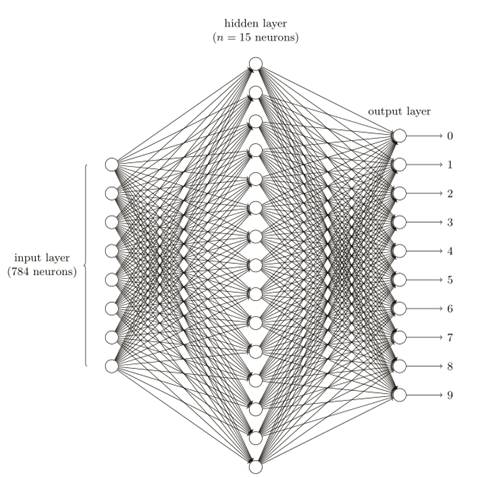
定義神經⽹絡后,讓我們回到⼿寫識別上來,我們將使⽤⼀個三層神經⽹絡來識別單個數字:
⽹絡的輸⼊層包含給輸⼊像素的值進⾏編碼的神經元,我們給⽹絡的訓練數據會有很多掃描得到的 28×28 的⼿寫數字的圖像組成,所有輸⼊層包含有 784 = 28×28個神經元。為了簡化,上圖中我已經忽略了 784 中⼤部分的輸⼊神經元。輸⼊像素是灰度級的,值為 0.0 表⽰⽩⾊,值為 1.0 表⽰⿊⾊,中間數值表⽰逐漸暗淡的灰⾊。
⽹絡的第⼆層是⼀個隱藏層,我們⽤ n 來表⽰神經元的數量,⽰例中⽤⼀個⼩的隱藏層來說明,僅僅包含 n = 15 個神經元,⽹絡的輸出層包含有 10 個神經元。如果第⼀個神經元激活,即輸出 ≈ 1,那么表明⽹絡認為數字是⼀個 0。如果第⼆個神經元激活,就表明⽹絡認為數字是⼀個 1。依此類推。更確切地說,我們把輸出神經元的輸出賦予編號 0 到 9,并計算出那個神經元有最⾼的激活值。⽐如,如果編號為 6 的神經元激活,那么我們的⽹絡會猜到輸⼊的數字是 6。
為什么我們⽤ 10 個輸出神經元,畢竟我們的任務是能讓神經⽹絡告訴我們哪個數字(0,1,2,...,9 )能和輸⼊圖⽚匹配。⼀個看起來更⾃然的⽅式就是使⽤ 4 個輸出神經元,這樣做難道效率不低嗎?最終的判斷是基于經驗主義的:我們可以實驗兩種不同的⽹絡設計,結果證明對于這個特定的問題⽽⾔,10 個輸出神經元的神經⽹絡⽐ 4 個的識別效果更好。
為了理解為什么我們這么做,我們需要從根本原理上理解神經⽹絡究竟在做些什么。⾸先考慮有 10 個神經元的情況。我們⾸先考慮第⼀個輸出神經元,它告訴我們⼀個數字是不是 0,它能那么做是因為可以權衡從隱藏層來的信息。隱藏層的神經元在做什么呢?假設隱藏層的第⼀個神經元只是⽤于檢測如下的圖像是否存在:
為了達到這個⽬的,它通過對此圖像對應部分的像素賦予較⼤權重,對其它部分賦予較⼩的權重,同理,我們可以假設隱藏層的第⼆,第三,第四個神經元是為檢測下列圖⽚是否存在:
就像你能猜到的,這四幅圖像組合在⼀起構成了前⾯顯⽰的⼀⾏數字圖像中的 0:
如果所有隱藏層的這四個神經元被激活那么我們就可以推斷出這個數字是 0,當然,這不是我們推斷出 0 的唯⼀⽅式,假設神經⽹絡以上述⽅式運⾏,我們可以給出⼀個貌似合理的理由去解釋為什么⽤ 10 個輸出⽽不是 4 個,如果我們有 4 個輸出,那么第⼀個輸出神經元將會盡⼒去判斷數字的最⾼有效位是什么,把數字的最⾼有效位和數字的形狀聯系起來并不是⼀個簡單的問題,很難想象出有什么恰當的歷史原因,⼀個數字的形狀要素會和⼀個數字的最⾼有效位有什么緊密聯系。
這個啟發性的⽅法通常很有效,它會節省你⼤量時間去設計⼀個好的神經⽹絡結構,筆者很喜歡這種試圖從道的層面解釋神經網絡的方法,它讓我們對于神經網絡的認識能更深一點,而不是人云亦云。
Part 3
使⽤梯度下降算法進⾏學習
這一節你能理解神經網絡到底要計算什么?為什么要這么計算?
現在我們有了神經⽹絡的設計,它怎樣可以學習識別數字呢?我們需要的第⼀樣東西是⼀個⽤來學習的數據集 —— 稱為訓練數據集。我們將使⽤ MNIST 數據集,其包含有數以萬計的連帶著正確分類器的⼿寫數字的掃描圖像,MNIST 數據分為兩個部分。第⼀部分包含 60,000 幅⽤于訓練數據的圖像。這些圖像掃描⾃250 ⼈的⼿寫樣本,他們中⼀半⼈是美國⼈⼝普查局的員⼯,⼀半⼈是⾼校學⽣,這些圖像是28 × 28 ⼤⼩的灰度圖像,第⼆部分是 10,000 幅⽤于測試數據的圖像,同樣是 28 × 28 的灰度圖像,我們將⽤這些測試數據來評估我們的神經⽹絡學會識別數字有多好。
我們將⽤符號 x 來表⽰⼀個訓練輸⼊。為了⽅便,把每個訓練輸⼊ x 看作⼀個 28×28 = 784維的向量,每個向量中的項⽬代表圖像中單個像素的灰度值。我們⽤ y = y(x) 表⽰對應的期望輸出,這⾥ y 是⼀個 10 維的向量。例如,如果有⼀個特定的畫成 6 的訓練圖像,x,那么y(x) = (0,0,0,0,0,0,1,0,0,0) T 則是⽹絡的期望輸出。注意這⾥ T 是轉置操作,把⼀個⾏向量轉換成⼀個列向量。
我們希望有⼀個算法,能讓我們找到權重和偏置,以⾄于⽹絡的輸出 y(x) 能夠擬合所有的訓練輸⼊ x。為了量化我們如何實現這個⽬標,我們定義⼀個代價函數,也叫損失函數或目標函數:
這⾥ w 表⽰所有的⽹絡中權重的集合,b 是所有的偏置,n 是訓練輸⼊數據的個數,a 是表⽰當輸⼊為 x 時輸出的向量,求和則是在總的訓練輸⼊ x 上進⾏的。當然,輸出 a 取決于 x, w和 b。
我們把 C 稱為⼆次代價函數;有時也稱被稱為均⽅誤差或者 MSE。觀察⼆次代價函數的形式我們可以看到 C(w,b) 是⾮負的,因為求和公式中的每⼀項都是⾮負的。此外,代價函數 C(w,b)的值相當⼩,即 C(w,b) ≈ 0,精確地說,是當對于所有的訓練輸⼊ x,y(x) 接近于輸出 a 時,因此如果我們的學習算法能找到合適的權重和偏置,使得 C(w,b) ≈ 0,它就能很好地⼯作,因此我們的訓練算法的⽬的,是最⼩化權重和偏置的代價函數 C(w,b),換句話說,我們想要找到⼀系列能讓代價盡可能⼩的權重和偏置,我們將采⽤稱為梯度下降的算法來達到這個⽬的。
為什么要介紹⼆次代價呢?畢竟我們最初感興趣的內容不是能正確分類的圖像數量嗎?為什么不試著直接最⼤化這個數量,⽽是去最⼩化⼀個類似⼆次代價的間接評量呢?這么做是因為在神經⽹絡中,被正確分類的圖像數量所關于權重和偏置的函數并不是⼀個平滑的函數,⼤多數情況下,對權重和偏置做出的微⼩變動完全不會影響被正確分類的圖像的數量,這會導致我們很難去解決如何改變權重和偏置來取得改進的性能,⽽⽤⼀個類似⼆次代價的平滑代價函數則能更好地去解決如何⽤權重和偏置中的微⼩的改變來取得更好的效。
這就是選擇MSE的原因,我們又有了一些悟道。
我們訓練神經⽹絡的⽬的是找到能最⼩化⼆次代價函數 C(w,b) 的權重和偏置,但是現在它有很多讓我們分散精⼒的結構 —— 對權重 w 和偏置 b 的解釋,晦澀不清的 σ 函數,神經⽹絡結構的選擇,MNIST 等等,事實證明我們可以忽略結構中⼤部分,把精⼒集中在最⼩化⽅⾯來理解它。
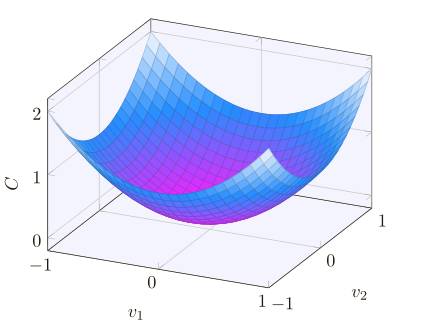
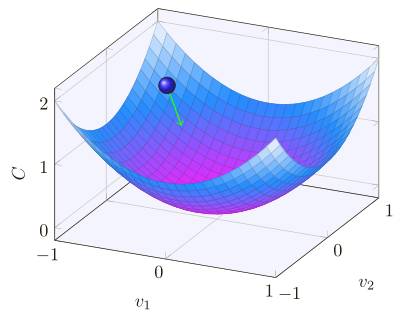
好了,假設我們要最⼩化某些函數,C(v),它可以是任意的多元實值函數,v = v 1 ,v 2 ,...。注意我們⽤ v 代替了 w 和 b 以強調它可能是任意的函數 —— 我們現在先不局限于神經⽹絡的環境。為了最⼩化 C(v),想象 C 是⼀個只有兩個變量 v1 和 v2 的函數:
我們想要的是找到 C 的全局最⼩值,當然,對于上圖的函數,我們⼀眼就能找到最⼩值,那意味著,也許我展⽰的函數過于簡單了!通常函數 C 可能是⼀個復雜的多元函數,看⼀下就能找到最⼩值可是不可能的。
找到最⼩值可是不可能的。⼀種解決這個問題的⽅式是⽤微積分來解析最⼩值。我們可以計算導數去尋找 C 的極值點。運⽓好的話,C 是⼀個只有⼀個或少數⼏個變量的函數,但是變量過多的話那就是噩夢,⽽且神經⽹絡中我們經常需要⼤量的變量—最⼤的神經⽹絡有依賴數億權重和偏置的代價函數,極其復雜,⽤微積分來計算最⼩值已經不可⾏了。
微積分是不能⽤了。幸運的是,有⼀個漂亮的推導法暗⽰有⼀種算法能得到很好的效果。⾸先把我們的函數想象成⼀個⼭⾕,只要瞄⼀眼上⾯的繪圖就不難理解,我們想象有⼀個⼩球從⼭⾕的斜坡滾落下來。我們的⽇常經驗告訴我們這個球最終會滾到⾕底。也許我們可以⽤這⼀想法來找到函數的最⼩值?我們會為⼀個(假想的)球體隨機選擇⼀個起始位置,然后模擬球體滾落到⾕底的運動。我們可以通過計算 C 的導數(或者⼆階導數)來簡單模擬——這些導數會告訴我們⼭⾕中局部“形狀”的⼀切,由此知道我們的球將怎樣滾動。
注意,知道我們的球將怎樣滾動這是核心。
為了更精確地描述這個問題,讓我們思考⼀下,當我們在 v1 和 v2 ⽅向分別將球體移動⼀個很⼩的量,即 ∆v1 和 ∆v2 時,球體將會發⽣什么情況,微積分告訴我們 C 將會有如下變化:
我們要尋找⼀種選擇 ∆v 1 和 ∆v 2 的⽅法使得 ∆C 為負;即,我們選擇它們是為了讓球體滾落,為了弄明⽩如何選擇,需要定義 ∆v 為 v 變化的向量,∆v ≡ (∆v1 ,∆v2 ) T ,T 是轉置符號,我們也定義 C 的梯度為偏導數的向量,⽤ ∇C 來表⽰梯度向量,即:
有了這些定義,∆C 的表達式可以被重寫為:
這個表達式解釋了為什么 ∇C 被稱為梯度向量:∇C 把 v 的變化關聯為 C 的變化,正如我們期望的⽤梯度來表⽰,但是這個⽅程真正讓我們興奮的是它讓我們看到了如何選取 ∆v 才能讓∆C 為負數,假設我們選取:
這⾥的η 是個很⼩的正數(稱為學習速率,注意以后會經常見到它),我們看到
這樣保證了∆C ≤ 0,即如果我們按照∆v方程這個規則去改變 v,那么 C 會⼀直減⼩,不會增加,這正是我們想要的特性,因此我們把∆v方程⽤于定義球體在梯度下降算法下的“運動定律”,也就是說我們⽤∆v方程計算∆v,來移動球體的位置 v:
然后我們⽤它再次更新規則來計算下⼀次移動。如果我們反復持續這樣做,我們將持續減⼩C 直到—— 正如我們希望的 —— 獲得⼀個全局的最⼩值。
總結⼀下,梯度下降算法⼯作的⽅式就是重復計算梯度 ∇C,然后沿著相反的⽅向移動,沿著⼭⾕“滾落”。我們可以想象它像這樣:
你可以把這個更新規則看做定義梯度下降算法。這給我們提供了⼀種⽅式去通過重復改變 v來找到函數 C 的最⼩值。這個規則并不總是有效的 —— 有⼏件事能導致錯誤,讓我們⽆法從梯度下降來求得函數 C 的全局最⼩值,這個觀點我們會在后⾯的去探討。但在實踐中,梯度下降算法通常⼯作地⾮常好,在神經⽹絡中這是⼀種⾮常有效的⽅式去求代價函數的最⼩值,進⽽促進⽹絡⾃⾝的學習。