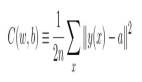神經網絡優化本質上是非凸的，但簡單的基于梯度的方法似乎總是能解決這樣的問題。這一現象是深度學習的核心支柱之一，并且也是我們很多理論學家試圖揭示的謎題。這篇文章將總結一些試圖攻克這一問題的近期研究，***還將討論我與 Sanjeev Arora、Noah Golowich 和 Wei Hu 合作的一篇新論文(arXiv：1810.02281)。該論文研究了深度線性神經網絡上梯度下降的情況，能保證以線性速率收斂到全局最小值。

[[249965]]

圖景(landscape)方法及其局限性

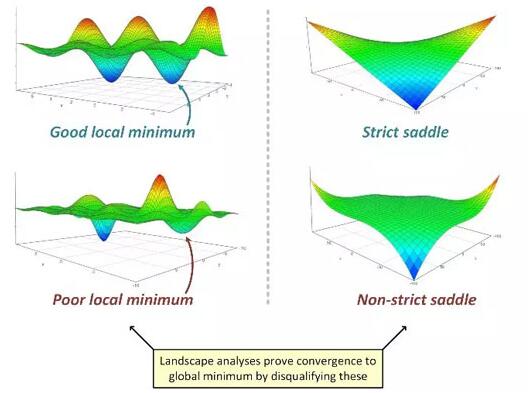
很多有關深度學習優化的論文都隱含地假設：在建立了損失圖景(尤其是臨界點的損失圖景，臨界點是指梯度消失的點)的幾何性質之后，就會得到對其的嚴格理解。舉個例子，通過類比凝聚態物理學的球形自旋玻璃模型，Choromanska et al. 2015 的論證變成了深度學習領域的一個猜想：

針對多種不同的涉及淺(兩層)模型的簡單問題的損失圖景，這一猜想的強形式已經得到了證明。這些簡單問題包括矩陣感知、矩陣完成、正交張量分解、相位恢復和具有二次激活的神經網絡。也有研究者在探究當圖景猜想成立時實現梯度下降到全局最小值的收斂，Rong Ge、Ben Recht、Chi Jin 和 Michael Jordan 的博客已經給出了很好的描述：

• http://www.offconvex.org/2016/03/22/saddlepoints/
• http://www.offconvex.org/2016/03/24/saddles-again/
• http://www.offconvex.org/2016/03/24/saddles-again/

他們描述了梯度下降可以如何通過逃避所有的嚴格鞍點來達到二階局部最小值(Hessian 為正半定的臨界點)，并還描述了當將擾動加入到該算法時這個過程是如何有效的。注意這是在圖景猜想下，即當沒有糟糕的局部最小值和非嚴格鞍點時，二階局部最小值可能也是全局最小值。

但是，很顯然，圖景方法(和圖景猜想)不能以這種方式應用于深度(三層或更多層)網絡。有多個原因。***，深度網絡通常會引入非嚴格鞍點(比如，在所有權重都為零的點，參見 Kawaguchi 2016)。第二，圖景角度很大程度上忽視了算法方面，而在實踐中算法方面對深度網絡的收斂有很大的影響——比如初始化或批歸一化的類型。***，正如我在之前的文章中談到的，基于 Sanjeev Arora 和 Elad Hazan 的研究，為經典線性模型添加(冗余的)線性層有時能為基于梯度的優化帶來加速，而不會給模型的表現力帶來任何增益，但是卻會為之前的凸問題引入非凸性。任何僅依靠臨界點性質的圖景分析都難以解釋這一現象，因為通過這樣的方法，因為優化一個具有單個臨界點且該臨界點是全局最小值的凸目標是最困難的。

解決方案?

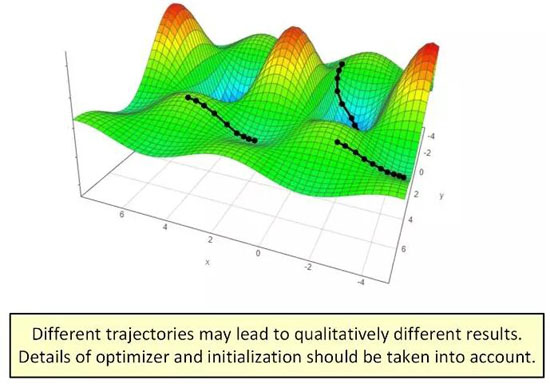
圖景方法在分析深度學習優化上的局限性說明它可能拋棄了太多重要細節。比起「圖景方法是否優雅」，也許更相關的問題是「來自特定初始化的特定優化器軌跡(trajectory)具有怎樣的行為?」

盡管基于軌跡的方法看起來比圖景方法繁重得多，但它已經帶來了可觀的進展。近期一些論文(比如 Brutzkus and Globerson 2017、Li and Yuan 2017、Zhong et al. 2017、Tian 2017、Brutzkus et al. 2018、Li et al. 2018、Du et al. 2018、Liao et al. 2018)已經采用了這一策略，并成功分析了不同類型的淺模型。此外，基于軌跡的分析也正開始涉足圖景方法之外的領域——對于線性神經網絡情況，他們已經成功確立在任意深度下梯度下降到全局最小值的收斂性。

對深度線性神經網絡的基于軌跡的分析

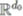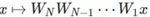線性神經網絡是使用線性激活或不使用激活的全連接神經網絡。具體來說，一個輸入維度為 d_0，輸出維度為 d_N 且隱藏維度為 d_1,d_2...d_{N-1} 的深度為 N 的線性網絡是到的線性映射，該映射被參數化為，其中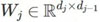是第 j 層的權重矩陣。盡管這樣表示看起來很簡單普通，但線性神經網絡在優化方面在某種程度上復雜得讓人驚訝——它們會導致具有多個最小值和鞍點的非凸訓練問題。被視為深度學習中優化的替代理論，基于梯度的算法在線性神經網絡上的應用在這段時間收到了極大的關注。

就我所知，Saxe et al. 2014 是***為深度(三或更多層)線性網絡執行了基于軌跡的分析，在白化的數據上處理最小化 ℓ2 損失的梯度流(學習率極小的梯度下降)。盡管這個分析有很重要的貢獻，但卻并未正式確立到全局最小值的收斂性，也沒有考慮計算復雜性方面(收斂所需的迭代次數)。近期研究 Bartlett et al. 2018 在填補這些空白上取得了進展，應用了基于軌跡的方法來分析用于線性殘差網絡特定案例的梯度下降，即所有層都有統一寬度(d_0=d_1=...=d_N)且同等初始化(W_j=I, ∀j)的線性網絡。考慮到數據-標簽分布各有不同(他們稱之為「targets」)，Bartlett 等人展示了可證明梯度下降以線性速率收斂到全局最小值的案例——在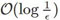次迭代后與***的損失小于 ϵ>0;還展示了無法收斂的情況。

在我與 Sanjeev Arora、Noah Golowich 和 Wei Hu 合作的一篇新論文中，我們在使用基于軌跡的方法方面又向前邁進了一步。具體而言，我們分析了任意不包含「瓶頸層」的線性神經網絡的梯度下降軌跡，瓶頸層是指其隱藏維度不小于輸入和輸出維度之間的最小值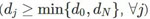;還證明了以線性速率到全局最小值的收斂性。但初始化需要滿足下面兩個條件：(1)近似平衡度(approximate balancedness)——;(2)缺值余量(deficiency margin)——初始損失小于任意秩缺失解的損失。我們證明這兩個條件都是必需的，違反其中任意一個都可能導致軌跡不收斂。在線性殘差網絡的特殊案例中，初始化時的近似平衡度很容易滿足，而且對于以零為中心的小隨機擾動進行初始化的自定義設置也同樣容易滿足。后者也會導致出現具有正概率的缺值余量。對于 d_N=1 的情況(即標量回歸)，我們提供了一個隨機初始化方案，能同時滿足這兩個條件，因此能以恒定概率以線性速率收斂到全局最小值。

我們分析的關鍵是觀察權重是否初始化到了近似平衡，它們會在梯度下降的整個迭代中一直這樣保持。換句話說，優化方法所采取的軌跡遵循一個特殊的特征：

其意思是在整個時間線中，所有層都有(接近)一樣的奇異值集合，而且每層的左側奇異值向量都與其后一層的右側奇異值向量(接近)一致。我們表明這種規律性意味著梯度下降能穩定運行，從而證明即使是在損失圖景整體很復雜的案例中(包括很多非嚴格鞍點)，它也可能會在優化器所取的特定軌跡周圍表現得特別良好。

總結

通過圖景方法解決深度學習中優化的問題在概念上很吸引人，即分析與訓練所用算法無關的目標的幾何性質。但是這一策略存在固有的局限性，主要是因為它要求整個目標都要優雅，這似乎是一個過于嚴格的要求。替代方法是將優化器及其初始化納入考量，并且僅沿所得到的軌跡關注其圖景。這種替代方法正得到越來越多的關注。圖景分析目前僅限于淺(兩層)模型，而基于軌跡的方法最近已經處理了任意深度的模型，證明了梯度下降能以線性速率收斂到全局最小值。但是，這一成功僅包含了線性神經網絡，還仍有很多工作有待完成。我預計基于軌跡的方法也將成為我們正式理解深度非線性網絡的基于梯度的優化的關鍵。

原文鏈接：http://www.offconvex.org/2018/11/07/optimization-beyond-landscape/

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文