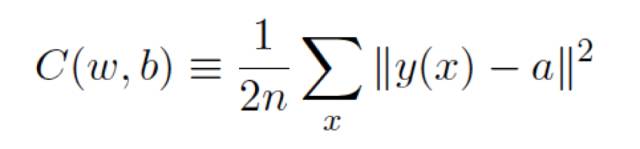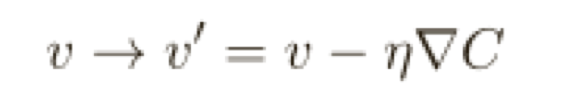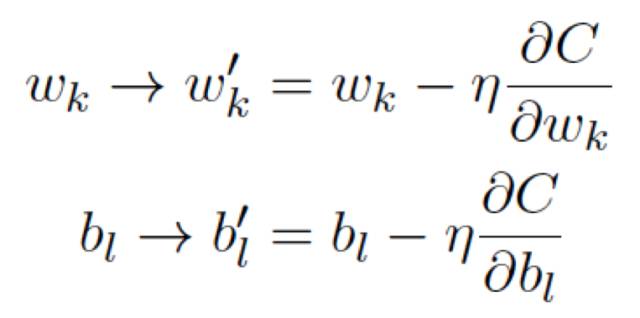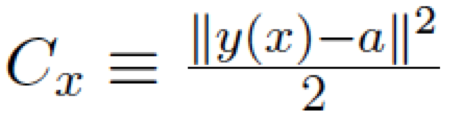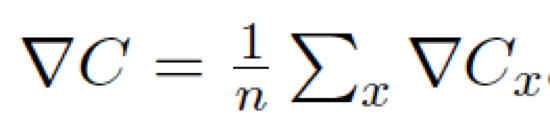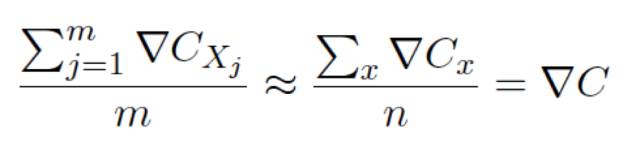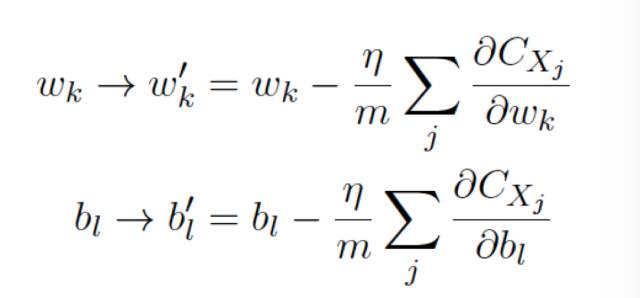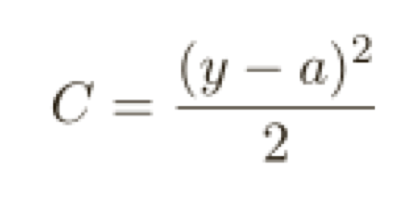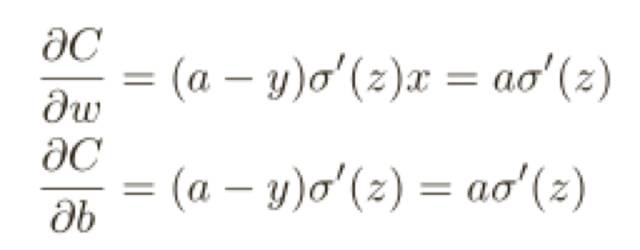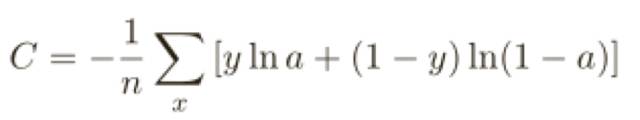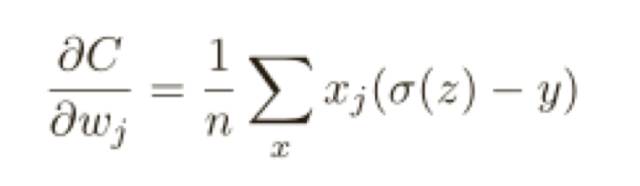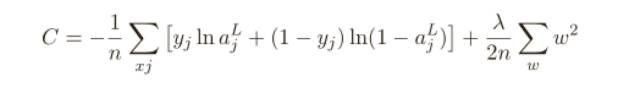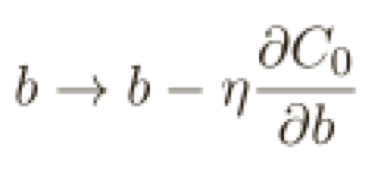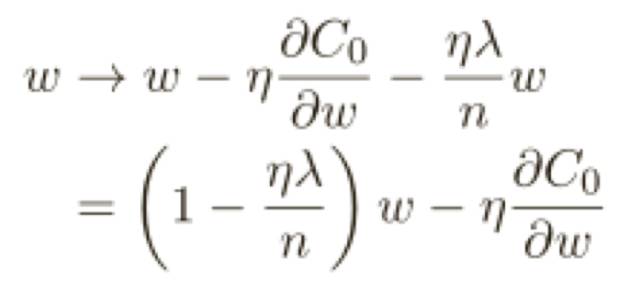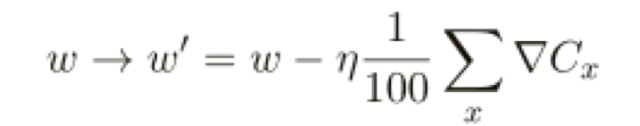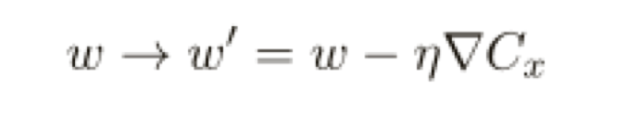這是你所有看到的有關(guān)神經(jīng)網(wǎng)絡(luò)參數(shù)的理解中最通俗易懂的一個(gè)了，公式也減到了最少，神經(jīng)網(wǎng)絡(luò)的專業(yè)人士繞道哦。

在上一篇《理解深度學(xué)習(xí)的鑰匙 –啟蒙篇》，我們提到定義⼀個(gè)二次代價(jià)函數(shù)，也叫損失函數(shù)或目標(biāo)函數(shù)：  

 

這⾥ w 表⽰所有的⽹絡(luò)中權(quán)重的集合，b 是所有的偏置，n 是訓(xùn)練輸⼊數(shù)據(jù)的個(gè)數(shù)，a 是表⽰當(dāng)輸⼊為 x 時(shí)輸出的向量，y(x)是實(shí)際輸出的向量，求和則是在總的訓(xùn)練輸⼊ x 上進(jìn)⾏的。

參考《理解深度學(xué)習(xí)的鑰匙 –啟蒙篇》文章C(v)中v的計(jì)算過(guò)程，∇C 來(lái)表示梯度向量：  

 

現(xiàn)在有兩個(gè)分量組成w 和b，⽽梯度向量∇C 則有相應(yīng)的分量∂C/∂w 和 ∂C/∂b，⽤這些分量來(lái)寫梯度下降的更新規(guī)則，我們得到： 

 

通過(guò)重復(fù)應(yīng)⽤這⼀更新規(guī)則我們就能“讓球體滾下⼭”，并且有望能找到代價(jià)函數(shù)的最⼩值，換句話說(shuō)，這是⼀個(gè)能讓神經(jīng)⽹絡(luò)學(xué)習(xí)的規(guī)則。

注意這個(gè)代價(jià)函數(shù)是遍及每個(gè)訓(xùn)練樣本的，x表示某一個(gè)樣本： 

 

 

在實(shí)踐中，為了計(jì)算梯度∇C，我們需要為每個(gè)訓(xùn)練輸⼊x 單獨(dú)地計(jì)算梯度值∇Cx，然后求平均值：  

 

 

不幸的是，當(dāng)訓(xùn)練輸⼊的數(shù)量過(guò)⼤時(shí)會(huì)花費(fèi)很⻓時(shí)間，這樣會(huì)使學(xué)習(xí)變得相當(dāng)緩慢。

1、隨機(jī)梯度下降

這一節(jié)你將了解具體的一個(gè)訓(xùn)練過(guò)程，了解什么叫作⼩批量數(shù)據(jù)(mini-batch)，什么叫作訓(xùn)練迭代期(epoch)。

有種叫做隨機(jī)梯度下降的算法能夠加速學(xué)習(xí)，其思想就是通過(guò)隨機(jī)選取⼩量訓(xùn)練輸⼊樣本來(lái)計(jì)算∇Cx，進(jìn)⽽估算梯度∇C，通過(guò)計(jì)算少量樣本的平均值我們可以快速得到⼀個(gè)對(duì)于實(shí)際梯度∇C 的很好的估算，這有助于加速梯度下降，進(jìn)⽽加速學(xué)習(xí)過(guò)程。

更準(zhǔn)確地說(shuō)，隨機(jī)梯度下降通過(guò)隨機(jī)選取⼩量的m 個(gè)訓(xùn)練輸⼊來(lái)⼯作，我們將這些隨機(jī)的訓(xùn)練輸⼊標(biāo)記為X1;X2… Xm，并把它們稱為⼀個(gè)⼩批量數(shù)據(jù)(mini-batch)。假設(shè)樣本數(shù)量m ⾜夠⼤，我們期望∇Cxj 的平均值⼤致相等于整個(gè)∇Cx 的平均值，即：  

 

 

可以推導(dǎo)得到：  

 

然后我們?cè)偬暨x另⼀隨機(jī)選定的⼩批量數(shù)據(jù)去訓(xùn)練，直到我們⽤完了所有的訓(xùn)練輸⼊，這被稱為完成了⼀個(gè)訓(xùn)練迭代期(epoch)。然后我們就會(huì)開(kāi)始⼀個(gè)新的訓(xùn)練迭代期。

我們可以把隨機(jī)梯度下降想象成⼀次⺠意調(diào)查：在⼀個(gè)⼩批量數(shù)據(jù)上采樣⽐對(duì)⼀個(gè)完整數(shù)據(jù)集進(jìn)⾏梯度下降分析要容易得多，正如進(jìn)⾏⼀次⺠意調(diào)查⽐舉⾏⼀次全⺠選舉要更容易。例如，如果我們有⼀個(gè)規(guī)模為n = 60000 的訓(xùn)練集，就像MNIST，并選取⼩批量數(shù)據(jù)⼤⼩為m=10，這意味著在估算梯度過(guò)程中加速了6000 倍。

現(xiàn)在讓我們寫⼀個(gè)學(xué)習(xí)如何識(shí)別⼿寫數(shù)字的程序，使⽤隨機(jī)梯度下降算法和MNIST

訓(xùn)練數(shù)據(jù)，除了MNIST 數(shù)據(jù)，我們還需要⼀個(gè)叫做Numpy 的Python 庫(kù)，⽤來(lái)做快速線性代數(shù)，不要怕，筆者不會(huì)貼代碼，只是示意一下，大家理解函數(shù)調(diào)用的方式即可：

在加載完MNIST 數(shù)據(jù)之后，我們將設(shè)置⼀個(gè)有784個(gè)像素輸入、30 個(gè)隱藏層神經(jīng)元、10個(gè)輸出的Network：  

 

我們將使⽤隨機(jī)梯度下降來(lái)從MNIST training_data 學(xué)習(xí)超過(guò)30 次迭代期，⼩批量數(shù)據(jù)⼤⼩為10，學(xué)習(xí)速率η=3.0:  

 

打印內(nèi)容顯⽰了在每輪訓(xùn)練期后神經(jīng)⽹絡(luò)能正確識(shí)別測(cè)試圖像的數(shù)量。正如你所⻅到，在僅僅⼀次迭代期后，達(dá)到了10,000 中選中的9,129 個(gè),⽽且數(shù)⽬還在持續(xù)增⻓，經(jīng)過(guò)訓(xùn)練的⽹絡(luò)給出的識(shí)別率約為95%:  

 

讓我們重新運(yùn)⾏上⾯的實(shí)驗(yàn)，將隱藏神經(jīng)元數(shù)量改到100:  

 

果然，它將結(jié)果提升⾄96.59%，⾄少在這種情況下，使⽤更多的隱藏神經(jīng)元幫助我們得到了更好的結(jié)果。

當(dāng)然，為了獲得這些準(zhǔn)確性，我不得不對(duì)訓(xùn)練的迭代期數(shù)量(epoch)，⼩批量數(shù)據(jù)⼤⼩(minbatch)和學(xué)習(xí)速率η做特別的選擇,正如我上⾯所提到的，這些在我們的神經(jīng)⽹絡(luò)中被稱為超參數(shù)，以區(qū)別于通過(guò)我們的學(xué)習(xí)算法所學(xué)到的參數(shù)(權(quán)重和偏置),如果我們選擇了糟糕的超參數(shù)，我們會(huì)得到較差的結(jié)果。

假如我們選定學(xué)習(xí)速率為η= 0.001：  

 

結(jié)果則不太令人鼓舞了： 

 

然⽽，你可以看到⽹絡(luò)的性能隨著時(shí)間的推移慢慢地變好了，這表明應(yīng)該增⼤學(xué)習(xí)速率，例如η= 0.01，如果我們那樣做了，我們會(huì)得到更好的結(jié)果，這表明我們應(yīng)該再次增加學(xué)習(xí)速率。(如果改變能夠改善⼀些事情，試著做更多!)如果我們這樣做⼏次，我們最終會(huì)得到⼀個(gè)像η=1.0 的學(xué)習(xí)速率(或者調(diào)整到3.0)，這跟我們之前的實(shí)驗(yàn)很接近。因此即使我們最初選擇了糟糕的超參數(shù)，我們⾄少獲得了⾜夠的信息來(lái)幫助我們改善對(duì)于超參數(shù)的選擇。

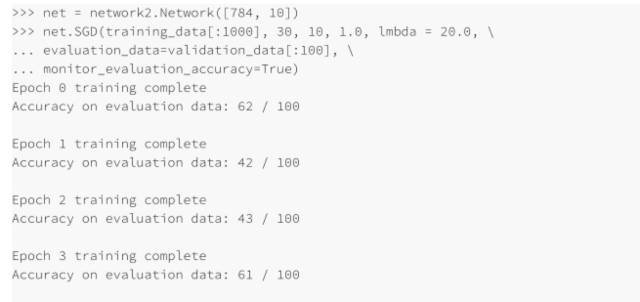
通常，調(diào)試⼀個(gè)神經(jīng)⽹絡(luò)是具有挑戰(zhàn)性的，尤其是當(dāng)初始的超參數(shù)的選擇產(chǎn)⽣的結(jié)果還不如隨機(jī)噪點(diǎn)的時(shí)候。假如我們?cè)?#12132;之前成功的具有30 個(gè)隱藏神經(jīng)元的⽹絡(luò)結(jié)構(gòu)，但是學(xué)習(xí)速率改為η= 100，在這點(diǎn)上，我們實(shí)際⾛的太遠(yuǎn)，學(xué)習(xí)速率太⾼了：  

 

我們可能不僅關(guān)⼼學(xué)習(xí)速率，還要關(guān)⼼我們的神經(jīng)⽹絡(luò)中的其它每⼀個(gè)部分，我們可能想知道是否⽤了讓⽹絡(luò)很難學(xué)習(xí)的初始權(quán)重和偏置?或者可能我們沒(méi)有⾜夠的訓(xùn)練數(shù)據(jù)來(lái)獲得有意義的學(xué)習(xí)?或者我們沒(méi)有進(jìn)⾏⾜夠的迭代期?或者可能對(duì)于具有這種結(jié)構(gòu)的神經(jīng)⽹絡(luò)，學(xué)習(xí)識(shí)別⼿寫數(shù)字是不可能的?可能學(xué)習(xí)速率太低?或者可能學(xué)習(xí)速率太⾼?當(dāng)你第⼀次遇到問(wèn)題，你不總是能有把握。

就像常規(guī)編程那樣，它是⼀⻔藝術(shù)，你需要學(xué)習(xí)調(diào)試的藝術(shù)來(lái)獲得神經(jīng)⽹絡(luò)更好的結(jié)果，更普通的是，我們需要啟發(fā)式⽅法來(lái)選擇好的超參數(shù)和好的結(jié)構(gòu)，后面將討論怎么樣選擇超參數(shù)。

2、邁向深度學(xué)習(xí)

這一節(jié)你將了解神經(jīng)網(wǎng)絡(luò)是如何過(guò)渡到深度學(xué)習(xí)的。

雖然我們的神經(jīng)網(wǎng)絡(luò)給出了令⼈印象深刻的表現(xiàn)，但這樣的表現(xiàn)帶有⼏分神秘，⽹絡(luò)中的權(quán)重和偏置是被⾃動(dòng)發(fā)現(xiàn)的，這意味著我們不能⽴即解釋⽹絡(luò)怎么做的、做了什么，我們能否找到⼀些方法來(lái)理解我們的⽹絡(luò)通過(guò)什么原理分類⼿寫數(shù)字?并且，在知道了這些原理后，我們能做得更好嗎?

為了讓這些問(wèn)題更具體，我們假設(shè)數(shù)⼗年后神經(jīng)⽹絡(luò)引發(fā)了⼈工智能(AI)。到那個(gè)時(shí)候，我們能明⽩這種智能⽹絡(luò)的⼯作機(jī)制嗎?或許，因?yàn)橛兄?#12163;動(dòng)學(xué)習(xí)得到的權(quán)重和偏置，這些是我們⽆法理解的，這樣的神經(jīng)⽹絡(luò)對(duì)我們來(lái)說(shuō)是不透明的。在⼈⼯智能的早期研究階段，⼈們希望在構(gòu)建⼈⼯智能的努⼒過(guò)程中，也同時(shí)能夠幫助我們理解智能背后的機(jī)制，以及⼈類⼤腦的運(yùn)轉(zhuǎn)⽅式，但結(jié)果可能是我們既不能夠理解⼤腦的機(jī)制，也不能夠理解⼈⼯智能的機(jī)制。

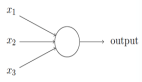
為解決這些問(wèn)題，讓我們重新思考⼀下我在本章開(kāi)始時(shí)所給的⼈⼯神經(jīng)元的解釋，作為⼀種衡量證據(jù)的方法，假設(shè)我們要確定⼀幅圖像是否顯⽰有⼈臉 ：  

[[188909]] 

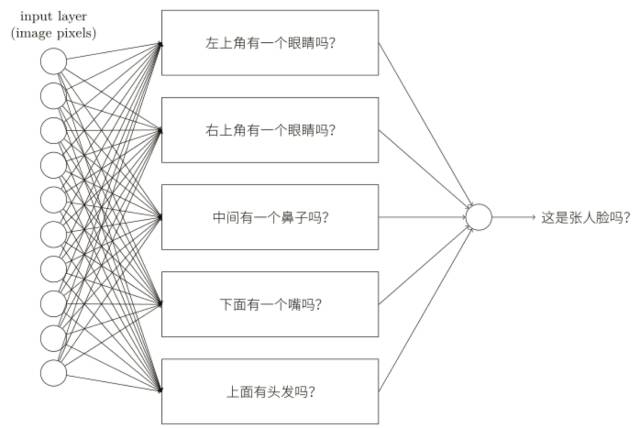
我們可以用解決⼿寫識(shí)別問(wèn)題的相同⽅式來(lái)攻克這個(gè)問(wèn)題 —— ⽹絡(luò)的輸⼊是圖像中的像素，⽹絡(luò)的輸出是⼀個(gè)單個(gè)的神經(jīng)元⽤于表明“是的，這是⼀張臉”或“不，這不是⼀張臉”，假設(shè)我們就采取了這個(gè)⽅法，但接下來(lái)我們先不去使⽤⼀個(gè)學(xué)習(xí)算法，⽽是去嘗試親⼿設(shè)計(jì)⼀個(gè)⽹絡(luò)，并為它選擇合適的權(quán)重和偏置。我們要怎樣做呢?暫時(shí)先忘掉神經(jīng)⽹絡(luò)，我們受到啟發(fā)的⼀個(gè)想法是將這個(gè)問(wèn)題分解成⼦問(wèn)題：圖像的左上⻆有⼀個(gè)眼睛嗎?右上⻆有⼀個(gè)眼睛嗎?中間有⼀個(gè)⿐⼦嗎?下⾯中央有⼀個(gè)嘴嗎?上⾯有頭發(fā)嗎?諸如此類，如果⼀些問(wèn)題的回答是“是”，或者甚⾄僅僅是“可能是”，那么我們可以作出結(jié)論這個(gè)圖像可能是⼀張臉，相反地，如果⼤多數(shù)這些問(wèn)題的答案是“不是”，那么這張圖像可能不是⼀張臉。

這個(gè)想法表明了如果我們能夠使用神經(jīng)⽹絡(luò)來(lái)解決這些⼦問(wèn)題，那么我們也許可以通過(guò)將這些解決⼦問(wèn)題的⽹絡(luò)結(jié)合起來(lái)，構(gòu)成⼀個(gè)⼈臉檢測(cè)的神經(jīng)⽹絡(luò)，下圖是⼀個(gè)可能的結(jié)構(gòu)，其中的⽅框表⽰⼦⽹絡(luò)，注意，這不是⼀個(gè)⼈臉檢測(cè)問(wèn)題的現(xiàn)實(shí)的解決⽅法，⽽是為了幫助我們構(gòu)建起⽹絡(luò)如何運(yùn)轉(zhuǎn)的直觀感受。  

 

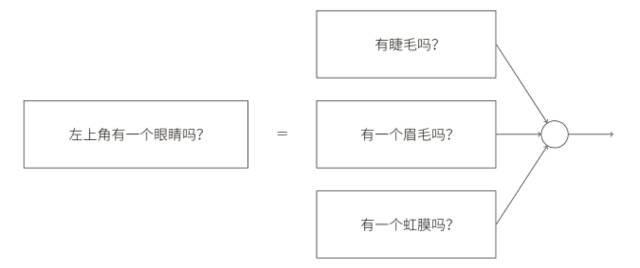
子網(wǎng)絡(luò)也可以被繼續(xù)分解，這看上去很合理，假設(shè)我們考慮這個(gè)問(wèn)題：“左上⻆有⼀個(gè)眼睛嗎?”這個(gè)問(wèn)題可以被分解成這些⼦問(wèn)題：“有⼀個(gè)眉⽑嗎?”，“有睫⽑嗎?”，“有虹膜嗎?”等等，當(dāng)然這些問(wèn)題也應(yīng)該包含關(guān)于位置的信息 —— 諸如“在左上⻆有眉⽑，上⾯有虹膜嗎?”——但是讓我們先保持簡(jiǎn)單，回答問(wèn)題“左上⻆有⼀個(gè)眼睛嗎?”的⽹絡(luò)能夠被分解成：  

 

這些子問(wèn)題也同樣可以繼續(xù)被分解，并通過(guò)多個(gè)⽹絡(luò)層傳遞得越來(lái)越遠(yuǎn)，最終，我們的⼦⽹絡(luò)可以回答那些只包含若⼲個(gè)像素點(diǎn)的簡(jiǎn)單問(wèn)題。舉例來(lái)說(shuō)，這些簡(jiǎn)單的問(wèn)題可能是詢問(wèn)圖像中的⼏個(gè)像素是否構(gòu)成⾮常簡(jiǎn)單的形狀，這些問(wèn)題就可以被那些與圖像中原始像素點(diǎn)相連的單個(gè)神經(jīng)元所回答，最終的結(jié)果是，我們?cè)O(shè)計(jì)出了⼀個(gè)⽹絡(luò)，它將⼀個(gè)⾮常復(fù)雜的問(wèn)題 —— 這張圖像是否有⼀張⼈臉 —— 分解成在單像素層⾯上就可回答的⾮常簡(jiǎn)單的問(wèn)題，它通過(guò)⼀系列多層結(jié)構(gòu)來(lái)完成，在前⾯的⽹絡(luò)層，它回答關(guān)于輸⼊圖像⾮常簡(jiǎn)單明確的問(wèn)題，在后⾯的⽹絡(luò)層，它建⽴了⼀個(gè)更加復(fù)雜和抽象的層級(jí)結(jié)構(gòu)，包含這種多層結(jié)構(gòu) —— 兩層或更多隱藏層 —— 的⽹絡(luò)被稱為深度神經(jīng)網(wǎng)絡(luò)。

⾃ 2006 年以來(lái)，⼈們已經(jīng)開(kāi)發(fā)了⼀系列技術(shù)使深度神經(jīng)網(wǎng)絡(luò)能夠?qū)W習(xí)，這些深度學(xué)習(xí)技術(shù)基于隨機(jī)梯度下降和反向傳播，并引進(jìn)了新的想法，這些技術(shù)已經(jīng)使更深(更⼤)的⽹絡(luò)能夠被訓(xùn)練 —— 現(xiàn)在訓(xùn)練⼀個(gè)有 5 到 10 層隱藏層的⽹絡(luò)都是很常⻅的，⽽且事實(shí)證明，在許多問(wèn)題上，它們⽐那些淺層神經(jīng)⽹絡(luò)，例如僅有⼀個(gè)隱藏層的⽹絡(luò)，表現(xiàn)的更加出⾊，當(dāng)然，原因是深度⽹絡(luò)能夠構(gòu)建起⼀個(gè)復(fù)雜的概念的層次結(jié)構(gòu)。

3、交叉熵代價(jià)函數(shù)

這一節(jié)你將了解神經(jīng)網(wǎng)絡(luò)訓(xùn)練速度太慢的原因，為什么要用交叉熵代價(jià)函數(shù)替代MSE或二次代價(jià)函數(shù)。

我們希望和期待神經(jīng)網(wǎng)絡(luò)可以從錯(cuò)誤中快速地學(xué)習(xí)，在實(shí)踐中，這種情況經(jīng)常出現(xiàn)嗎?為了回答這個(gè)問(wèn)題，讓我們看看⼀個(gè)⼩例⼦，這個(gè)例⼦包含⼀個(gè)只有⼀個(gè)輸入的神經(jīng)元：  

 

我們會(huì)訓(xùn)練這個(gè)神經(jīng)元來(lái)做⼀件非常簡(jiǎn)單的事：讓輸⼊ 1 轉(zhuǎn)化為 0。當(dāng)然，這很簡(jiǎn)單了，⼿⼯找到合適的權(quán)重和偏置就可以了，然⽽，看起來(lái)使⽤梯度下降的⽅式來(lái)學(xué)習(xí)權(quán)重和偏置是很有啟發(fā)的，所以，我們來(lái)看看神經(jīng)元如何學(xué)習(xí)。

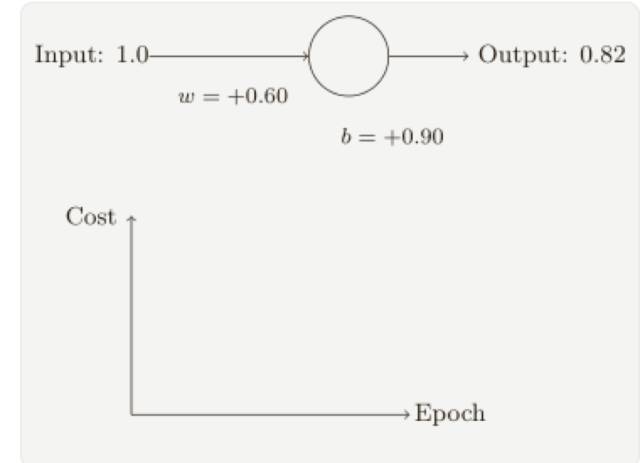
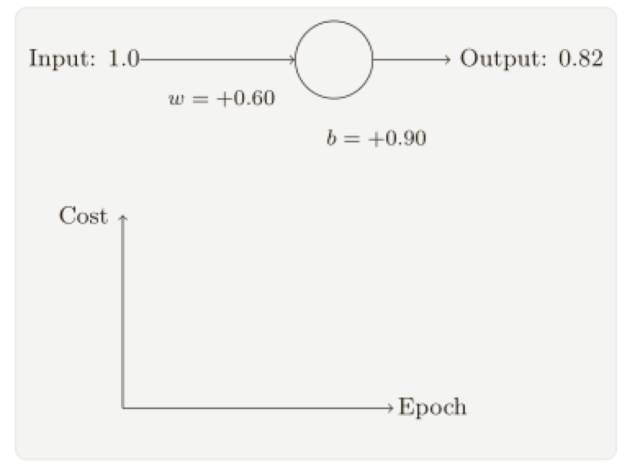
為了讓這個(gè)例⼦更明確，我會(huì)⾸先將權(quán)重和偏置初始化為 0.6 和 0.9。這些就是⼀般的開(kāi)始學(xué)習(xí)的選擇，并沒(méi)有任何刻意的想法。⼀開(kāi)始的神經(jīng)元的輸出是 0.82，所以這離我們的⽬標(biāo)輸出0.0 還差得很遠(yuǎn)，從下圖來(lái)看看神經(jīng)元如何學(xué)習(xí)到讓輸出接近 0.0 的，注意這些圖像實(shí)際上是正在進(jìn)⾏梯度的計(jì)算，然后使⽤梯度更新來(lái)對(duì)權(quán)重和偏置進(jìn)⾏更新，并且展⽰結(jié)果，設(shè)置學(xué)習(xí)速率 η = 0.15 進(jìn)行學(xué)習(xí)⼀⽅⾯⾜夠慢的讓我們跟隨學(xué)習(xí)的過(guò)程，另⼀⽅⾯也保證了學(xué)習(xí)的時(shí)間不會(huì)太久，⼏秒鐘應(yīng)該就⾜夠了，代價(jià)函數(shù)就是MSE，C。  

 

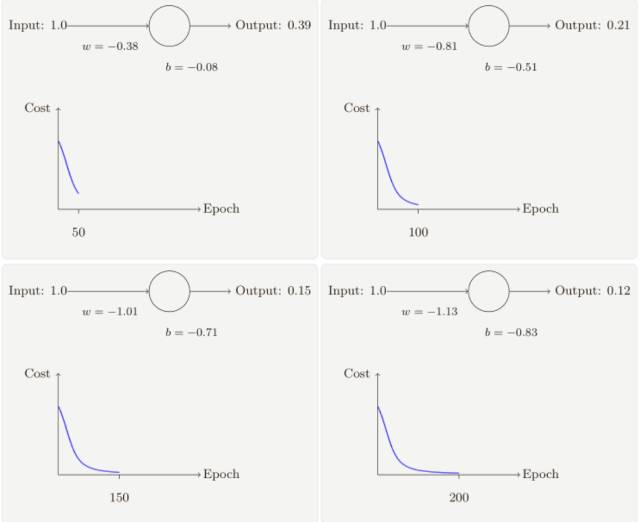
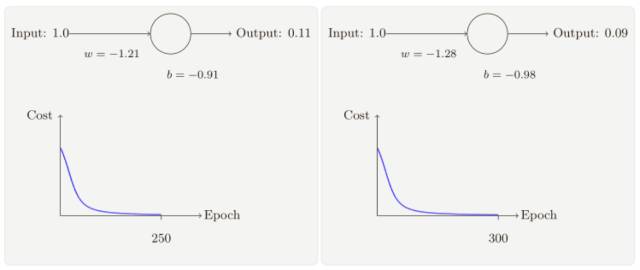
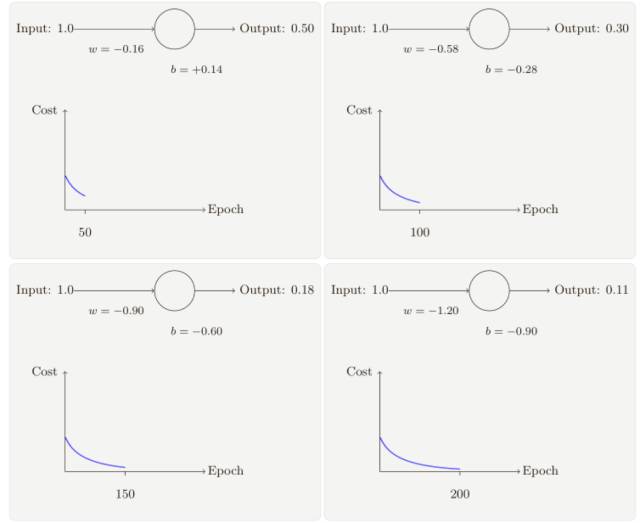
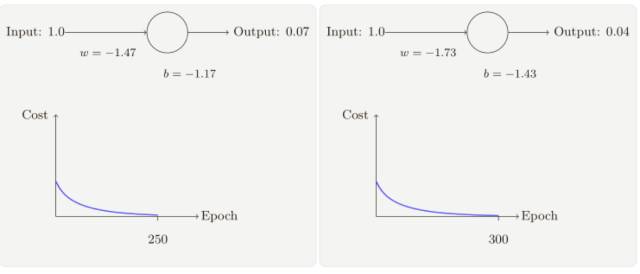
隨著迭代期的增加，神經(jīng)元的輸出、權(quán)重、偏置和代價(jià)的變化如下⾯⼀系列圖形所⽰：  

  

 

正如你所⻅，神經(jīng)元快速地學(xué)到了使得代價(jià)函數(shù)下降的權(quán)重和偏置，給出了最終的輸出為0.09，這雖然不是我們的目標(biāo)輸出 0.0，但是已經(jīng)挺好了。

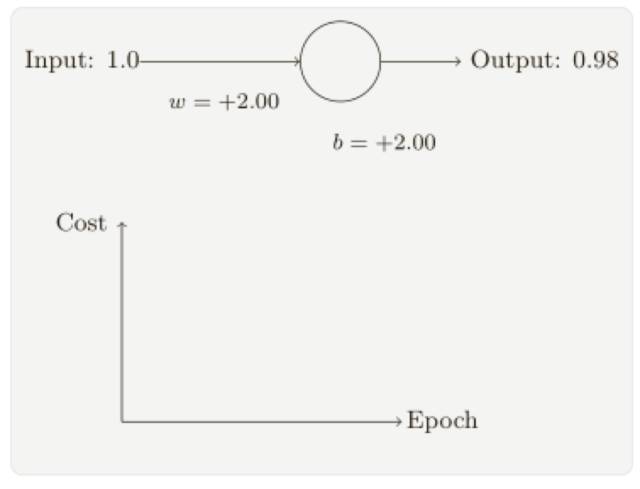
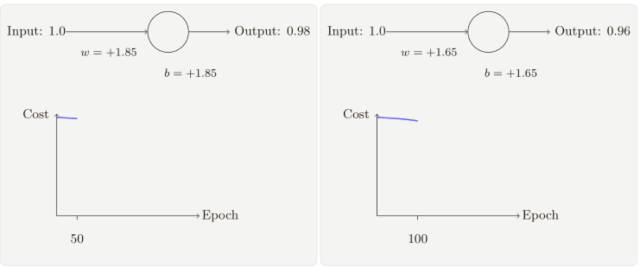
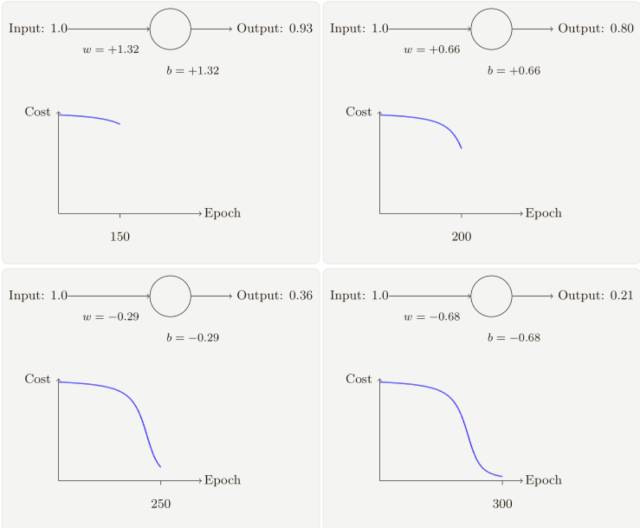
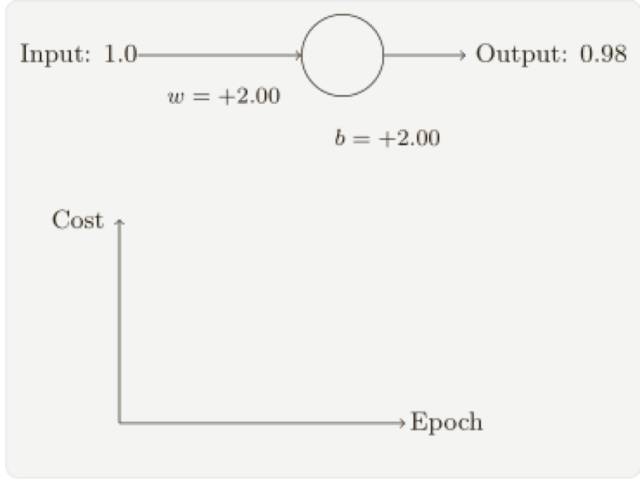
假設(shè)我們現(xiàn)在將初始權(quán)重和偏置都設(shè)置為 2.0，此時(shí)初始輸出為 0.98，這是和目標(biāo)值的差距相當(dāng)⼤的，現(xiàn)在看看神經(jīng)元學(xué)習(xí)的過(guò)程。  

 

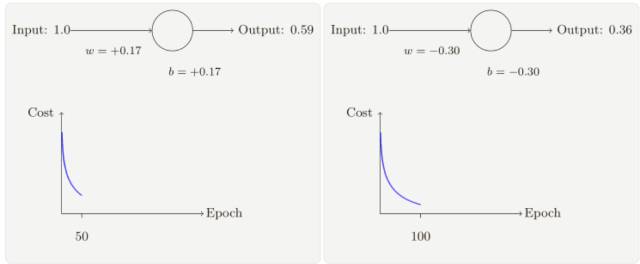
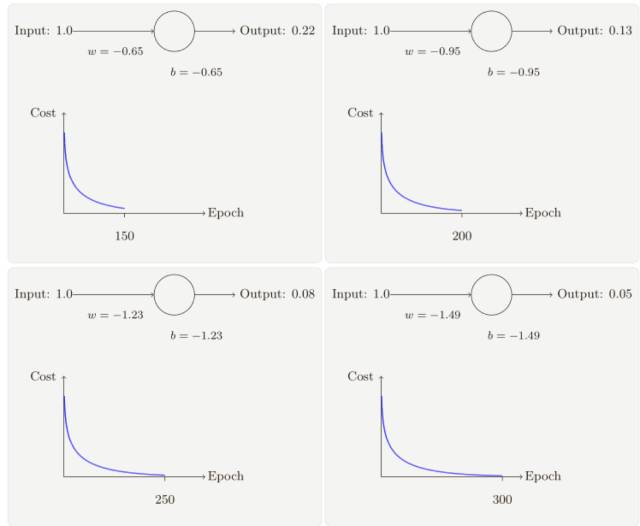
你將看到如下的⼀系列變化：  

  

 

雖然這個(gè)例⼦使用了同樣的學(xué)習(xí)速率(η = 0.15)，我們可以看到剛開(kāi)始的學(xué)習(xí)速度是⽐較緩慢的，對(duì)前 150 左右的學(xué)習(xí)次數(shù)，權(quán)重和偏置并沒(méi)有發(fā)⽣太⼤的變化，隨后學(xué)習(xí)速度加快，與上⼀個(gè)例⼦中類似了，神經(jīng)⽹絡(luò)的輸出也迅速接近 0.0。

這種行為看起來(lái)和⼈類學(xué)習(xí)⾏為差異很，我們通常是在犯錯(cuò)⽐較明顯的時(shí)候?qū)W習(xí)的速度最快，但是我們已經(jīng)看到了⼈⼯神經(jīng)元在其犯錯(cuò)較⼤的情況下其實(shí)學(xué)習(xí)很有難度，⽽且，這種現(xiàn)象不僅僅是在這個(gè)⼩例⼦中出現(xiàn)，也會(huì)在更加⼀般的神經(jīng)⽹絡(luò)中出現(xiàn)，為何學(xué)習(xí)如此緩慢?我們能夠找到避免這種情況的方法嗎?

為了理解這個(gè)問(wèn)題的源頭，想想我們的神經(jīng)元是通過(guò)改變權(quán)重和偏置，并以⼀個(gè)代價(jià)函數(shù)的偏導(dǎo)數(shù)(∂C/∂w 和 ∂C/∂b)決定的速度學(xué)習(xí)，所以，我們?cè)谡f(shuō)“學(xué)習(xí)緩慢”時(shí)，實(shí)際上就是說(shuō)這些偏導(dǎo)數(shù)很⼩，理解他們?yōu)楹芜@么⼩就是我們⾯臨的挑戰(zhàn)，為了理解這些，讓我們計(jì)算偏導(dǎo)數(shù)看看，我們⼀直在⽤的是⼆次代價(jià)函數(shù)，定義如下： 

 

其中 a 是神經(jīng)元的輸出，訓(xùn)練輸⼊為 x = 1，y = 0 則是⽬標(biāo)輸出,顯式地使⽤權(quán)重和偏置來(lái)表達(dá)這個(gè)，我們有 a = σ(z)，其中 z = wx + b，使用鏈?zhǔn)椒▌t來(lái)求權(quán)重和偏置的偏導(dǎo)數(shù)就有：  

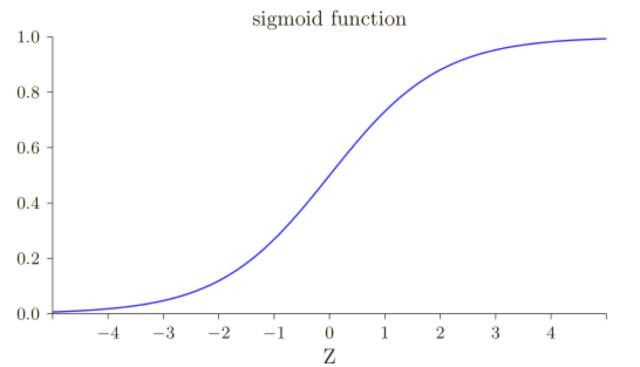
 其中我已經(jīng)將 x = 1 和 y = 0 代⼊了。為了理解這些表達(dá)式的行為，讓我們仔細(xì)看 σ ′ (z) 這⼀項(xiàng)，⾸先回憶⼀下 σ 函數(shù)圖像： 

 

 

我們可以從這幅圖看出，當(dāng)神經(jīng)元的輸出接近 1 的時(shí)候，曲線變得相當(dāng)平，所以 σ ′ (z) 就很⼩了，也即∂C/∂w 和 ∂C/∂b 會(huì)⾮常⼩，這其實(shí)就是學(xué)習(xí)緩慢的原因所在，⽽且，我們后面也會(huì)提到，這種學(xué)習(xí)速度下降的原因?qū)嶋H上也是更加⼀般的神經(jīng)⽹絡(luò)學(xué)習(xí)緩慢的原因，并不僅僅是在這個(gè)特例中特有的。

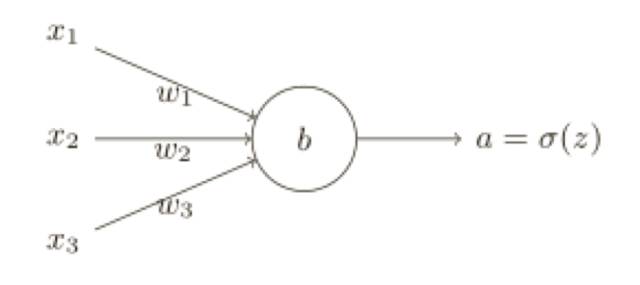
研究表明，我們可以通過(guò)使用交叉熵代價(jià)函數(shù)來(lái)替換⼆次代價(jià)函數(shù)，為了理解什么是交叉熵，我們稍微改變⼀下之前的簡(jiǎn)單例⼦，假設(shè)，我們現(xiàn)在要訓(xùn)練⼀個(gè)包含若⼲輸⼊變量的的神經(jīng)元，x1 ,x2 ,... 對(duì)應(yīng)的權(quán)重為 w1 ,w2 ,... 和偏置 b：  

 

神經(jīng)元的輸出就是 a = σ(z)，其中 z =∑j W j X j+ b 是輸⼊的帶權(quán)和，我們?nèi)缦露x這個(gè)神經(jīng)元的交叉熵代價(jià)函數(shù)：  

 

其中 n 是訓(xùn)練數(shù)據(jù)的總數(shù)，求和是在所有的訓(xùn)練輸⼊ x 上進(jìn)⾏的，y 是對(duì)應(yīng)的⽬標(biāo)輸出，在解決學(xué)習(xí)緩慢前，我們來(lái)看看交叉熵為何能夠解釋成⼀個(gè)代價(jià)函數(shù)。

如果對(duì)于所有的訓(xùn)練輸⼊ x，神經(jīng)元實(shí)際的輸出接近⽬標(biāo)值，那么交叉熵將接近 0，假設(shè)在這個(gè)例⼦中，y = 0 ⽽ a ≈ 0，交叉熵接近于0，反之，y = 1 ⽽ a ≈ 1，交叉熵也接近于0，綜上所述，交叉熵是⾮負(fù)的，在神經(jīng)元達(dá)到很好的正確率的時(shí)候會(huì)接近 0，這些其實(shí)就是我們想要的代價(jià)函數(shù)的特性，其實(shí)這些特性也是⼆次代價(jià)函數(shù)具備的，所以，交叉熵就是很好的選擇了。

但是交叉熵代價(jià)函數(shù)有⼀個(gè)⽐二次代價(jià)函數(shù)更好的特性就是它避免了學(xué)習(xí)速度下降的問(wèn)題，為了弄清楚這個(gè)情況，我們來(lái)算算交叉熵函數(shù)關(guān)于權(quán)重的偏導(dǎo)數(shù)，只列出結(jié)果：  

 

這是⼀個(gè)優(yōu)美的公式，它告訴我們權(quán)重學(xué)習(xí)的速度受到 σ(z) − y，也就是輸出中的誤差的控制，更大的誤差，更快的學(xué)習(xí)速度，這是我們直覺(jué)上期待的結(jié)果。特別地，這個(gè)代價(jià)函數(shù)還避免了像在⼆次代價(jià)函數(shù)中類似⽅程中 σ ′ (z) 導(dǎo)致的學(xué)習(xí)緩慢。

讓我們重回最原初的例⼦，來(lái)看看換成了交叉熵之后的學(xué)習(xí)過(guò)程，現(xiàn)在仍然按照前⾯的參數(shù)配置來(lái)初始化⽹絡(luò)，開(kāi)始權(quán)重為 0.6，而偏置為 0.9。  

 

看看在換成交叉熵之后⽹絡(luò)的學(xué)習(xí)情況，你將看到如下變化的曲線：  

 

 

毫不奇怪，在這個(gè)例子中，神經(jīng)元學(xué)習(xí)得相當(dāng)出⾊，跟之前差不多，現(xiàn)在我們?cè)倏纯粗俺鰡?wèn)題的那個(gè)例⼦(鏈接)，權(quán)重和偏置都初始化為 2.0：  

 

你將看到如下變化的曲線： 

 

 

 

 

成功了!這次神經(jīng)元的學(xué)習(xí)速度相當(dāng)快，跟我們預(yù)期的那樣，如果你觀測(cè)的⾜夠仔細(xì)，你可以發(fā)現(xiàn)代價(jià)函數(shù)曲線要⽐二次代價(jià)函數(shù)訓(xùn)練前⾯部分要陡很多，那個(gè)交叉熵導(dǎo)致的陡度讓我們⾼興，這正是我們期待的當(dāng)神經(jīng)元開(kāi)始出現(xiàn)嚴(yán)重錯(cuò)誤時(shí)能以最快速度學(xué)習(xí)。

4、過(guò)度擬合

這一節(jié)你將了解過(guò)度擬合的一般原因和解決策略。

諾貝爾獎(jiǎng)獲得者，物理學(xué)家恩⾥科·費(fèi)⽶有⼀次被問(wèn)到他對(duì)⼀些同僚提出的⼀個(gè)數(shù)學(xué)模型的意⻅，這個(gè)數(shù)學(xué)模型嘗試解決⼀個(gè)重要的未解決的物理難題。模型和實(shí)驗(yàn)⾮常匹配，但是費(fèi)⽶卻對(duì)其產(chǎn)⽣了懷疑。他問(wèn)模型中需要設(shè)置的⾃由參數(shù)有多少個(gè)。答案是“4”。費(fèi)⽶回答道 6 ：“我記得我的朋友約翰·馮·諾伊曼過(guò)去常說(shuō)，有四個(gè)參數(shù)，我可以模擬⼀頭⼤象，⽽有五個(gè)參數(shù)，我還能讓他卷鼻⼦。”

這⾥，其實(shí)是說(shuō)擁有大量的⾃由參數(shù)的模型能夠描述特別神奇的現(xiàn)象。即使這樣的模型能夠很好的擬合已有的數(shù)據(jù)，但并不表⽰是⼀個(gè)好模型。因?yàn)檫@可能只是因?yàn)槟Ｐ椭?#12188;夠的⾃由度使得它可以描述⼏乎所有給定⼤⼩的數(shù)據(jù)集，⽽不需要真正洞察現(xiàn)象的本質(zhì)。所以發(fā)⽣這種情形時(shí)，模型對(duì)已有的數(shù)據(jù)會(huì)表現(xiàn)的很好，但是對(duì)新的數(shù)據(jù)很難泛化，對(duì)⼀個(gè)模型真正的測(cè)驗(yàn)就是它對(duì)沒(méi)有⻅過(guò)的場(chǎng)景的預(yù)測(cè)能⼒。

費(fèi)米和馮·諾伊曼對(duì)有四個(gè)參數(shù)的模型就開(kāi)始懷疑了，我們⽤來(lái)對(duì) MNIST 數(shù)字分類的 30 個(gè)隱藏神經(jīng)元神經(jīng)⽹絡(luò)擁有將近 24,000 個(gè)參數(shù)!當(dāng)然很多，我們有 100 個(gè)隱藏元的⽹絡(luò)擁有將近80,000 個(gè)參數(shù)，⽽⽬前最先進(jìn)的深度神經(jīng)⽹絡(luò)包含百萬(wàn)級(jí)或者⼗億級(jí)的參數(shù)。我們應(yīng)當(dāng)信賴這些結(jié)果么?

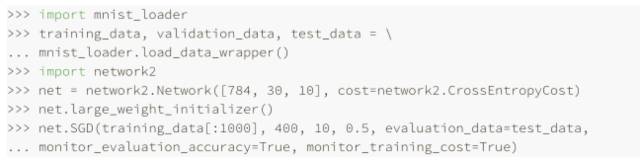
讓我們通過(guò)構(gòu)造⼀個(gè)網(wǎng)絡(luò)泛華能⼒很差的例⼦使這個(gè)問(wèn)題更清晰。我們的⽹絡(luò)有 30 個(gè)隱藏神經(jīng)元，共 23,860 個(gè)參數(shù)，但是我們不會(huì)使⽤所有 50,000 幅 MNIST 訓(xùn)練圖像，相反，我們只使⽤前 1,000 幅圖像。使⽤這個(gè)受限的集合，會(huì)讓泛化的問(wèn)題突顯。我們按照之前同樣的⽅式，使⽤交叉熵代價(jià)函數(shù)，學(xué)習(xí)速率設(shè)置為 η = 0.5 ⽽⼩批量數(shù)據(jù)⼤⼩設(shè)置為 10，不過(guò)這⾥我們要訓(xùn)練 400 個(gè)迭代期，⽐前⾯的要多⼀些，因?yàn)槲覀冎?#12132;了少量的訓(xùn)練樣本。 

 

 

 

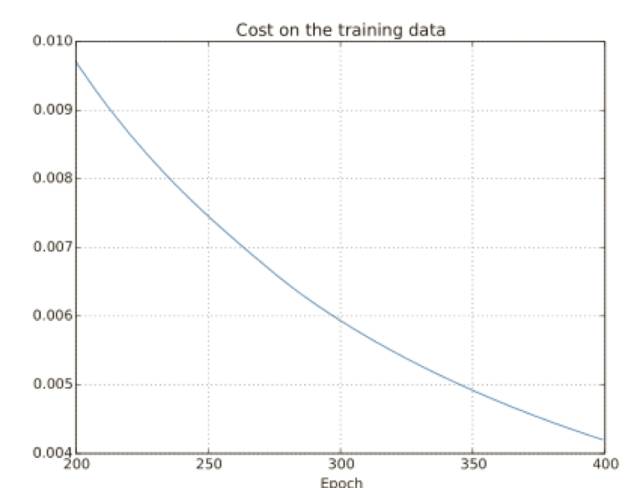
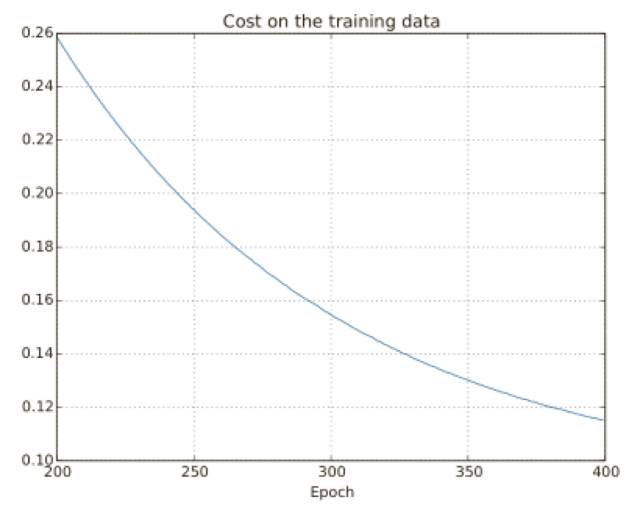
使⽤上面的結(jié)果，我們可以畫出當(dāng)⽹絡(luò)學(xué)習(xí)時(shí)代價(jià)變化的情況：

 

 

這看起來(lái)令人振奮，因?yàn)榇鷥r(jià)函數(shù)有⼀個(gè)光滑的下降，跟我們預(yù)期⼀致。注意，我只是展⽰了 200 到 399 迭代期的情況。

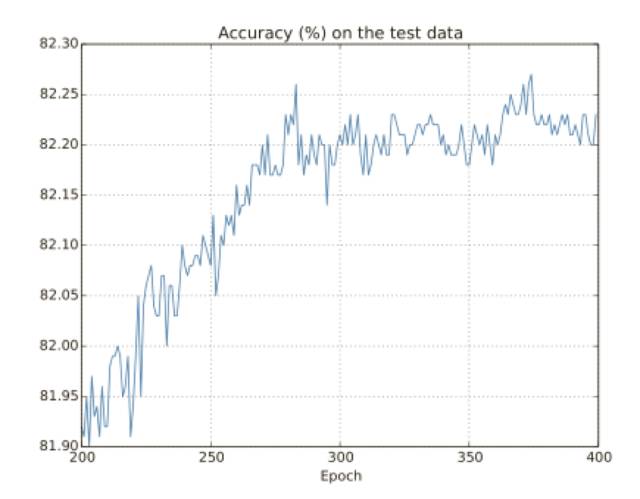
讓我們看看分類準(zhǔn)確率在測(cè)試集上的表現(xiàn)： 

 

 

 

這里我還是聚焦到了后⾯的過(guò)程。在前 200 迭代期(圖中沒(méi)有顯⽰)中準(zhǔn)確率提升到了 82%。然后學(xué)習(xí)逐漸變緩，最終，在 280 迭代期左右分類準(zhǔn)確率就停⽌了增⻓，后⾯的迭代期，僅僅看到了在 280 迭代期準(zhǔn)確率周圍隨機(jī)的⼩波動(dòng)，將這幅圖和前⾯的圖進(jìn)⾏對(duì)⽐，前⾯的圖中和訓(xùn)練數(shù)據(jù)相關(guān)的代價(jià)持續(xù)平滑下降，如果我們只看那個(gè)代價(jià)，會(huì)發(fā)現(xiàn)我們模型的表現(xiàn)變得“更好”，但是測(cè)試準(zhǔn)確率展⽰了提升只是⼀種假象，就像費(fèi)⽶不⼤喜歡的那個(gè)模型⼀樣，我們的⽹絡(luò)在 280 迭代期后就不在能夠推⼴到測(cè)試數(shù)據(jù)上，所以這不是有⽤的學(xué)習(xí)，我們說(shuō)⽹絡(luò)在 280迭代期后就過(guò)度擬合(overfitting)或者過(guò)度訓(xùn)練(overtraining)了。

所以我們的網(wǎng)絡(luò)實(shí)際上在學(xué)習(xí)訓(xùn)練數(shù)據(jù)集的特例，⽽不是能夠⼀般地進(jìn)⾏識(shí)別，我們的⽹絡(luò)⼏乎是在單純記憶訓(xùn)練集合，⽽沒(méi)有對(duì)數(shù)字本質(zhì)進(jìn)⾏理解能夠泛化到測(cè)試數(shù)據(jù)集上。

過(guò)度擬合是神經(jīng)網(wǎng)絡(luò)的⼀個(gè)主要問(wèn)題。這在現(xiàn)代⽹絡(luò)中特別正常，因?yàn)?#12153;絡(luò)權(quán)重和偏置數(shù)量巨⼤，為了⾼效地訓(xùn)練，我們需要⼀種檢測(cè)過(guò)度擬合是不是發(fā)⽣的技術(shù)，這樣我們不會(huì)過(guò)度訓(xùn)練，并且我們也想要找到⼀些技術(shù)來(lái)降低過(guò)度擬合的影響。

檢測(cè)過(guò)度擬合的明顯方法是使⽤上⾯的⽅法 —— 跟蹤測(cè)試數(shù)據(jù)集合上的準(zhǔn)確率隨訓(xùn)練變化情況，如果我們看到測(cè)試數(shù)據(jù)上的準(zhǔn)確率不再提升，那么我們就停⽌訓(xùn)練。當(dāng)然，嚴(yán)格地說(shuō)，這其實(shí)并⾮是過(guò)度擬合的⼀個(gè)必要現(xiàn)象，因?yàn)闇y(cè)試集和訓(xùn)練集上的準(zhǔn)確率可能會(huì)同時(shí)停⽌提升，當(dāng)然，采⽤這樣的策略是可以阻⽌過(guò)度擬合的。

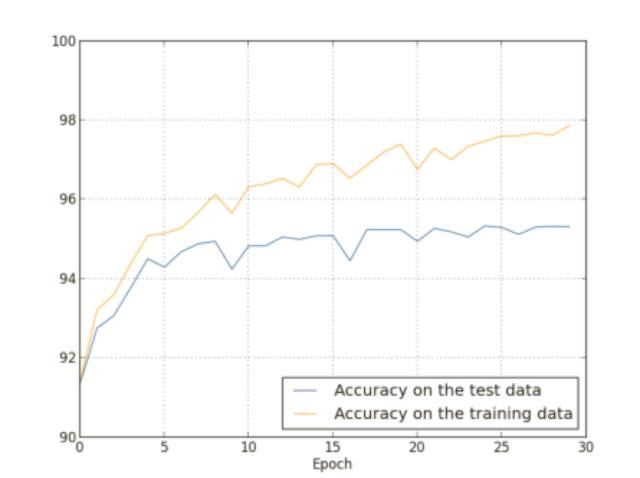
我們已經(jīng)研究了只使⽤ 1,000 幅訓(xùn)練圖像時(shí)的過(guò)度擬合問(wèn)題。那么如果我們使⽤所有的50,000 幅圖像的訓(xùn)練數(shù)據(jù)會(huì)發(fā)⽣什么?我們會(huì)保留所有其它的參數(shù)都⼀樣(30 個(gè)隱藏元，學(xué)習(xí)速率 0.5，小批量數(shù)據(jù)規(guī)模為 10)，但是迭代期為 30 次，下圖展⽰了分類準(zhǔn)確率在訓(xùn)練和測(cè)試集上的變化情況。 

 

 

如你所⻅，測(cè)試集和訓(xùn)練集上的準(zhǔn)確率相⽐我們使⽤ 1,000 個(gè)訓(xùn)練數(shù)據(jù)時(shí)相差更小。特別地，在訓(xùn)練數(shù)據(jù)上的最佳的分類準(zhǔn)確率 97.86% 只⽐測(cè)試集上的 95.33% 準(zhǔn)確率⾼了 1.53%。⽽之前的例⼦中，這個(gè)差距是 17.73%!過(guò)度擬合仍然發(fā)⽣了，但是已經(jīng)減輕了不少，我們的⽹絡(luò)從訓(xùn)練數(shù)據(jù)上更好地泛化到了測(cè)試數(shù)據(jù)上，⼀般來(lái)說(shuō)，最好的降低過(guò)度擬合的⽅式之⼀就是增加訓(xùn)練樣本的量，有了⾜夠的訓(xùn)練數(shù)據(jù)，就算是⼀個(gè)規(guī)模⾮常⼤的⽹絡(luò)也不⼤容易過(guò)度擬合，不幸的是，訓(xùn)練數(shù)據(jù)其實(shí)是很難或者很昂貴的資源，所以這不是⼀種太切實(shí)際的選擇。

5、規(guī)范化

這一節(jié)你將了解用規(guī)范化方法來(lái)防止過(guò)度擬合的方法，但無(wú)法給出科學(xué)的解釋。

增加訓(xùn)練樣本的數(shù)量是⼀種減輕過(guò)度擬合的方法，還有其他的⼀下⽅法能夠減輕過(guò)度擬合的程度嗎?⼀種可⾏的⽅式就是降低⽹絡(luò)的規(guī)模。然⽽，⼤的⽹絡(luò)擁有⼀種⽐⼩⽹絡(luò)更強(qiáng)的潛⼒，所以這⾥存在⼀種應(yīng)⽤冗余性的選項(xiàng)，幸運(yùn)的是，還有其他的技術(shù)能夠緩解過(guò)度擬合，即使我們只有⼀個(gè)固定的⽹絡(luò)和固定的訓(xùn)練集合，這種技術(shù)就是規(guī)范化。

本節(jié)，我會(huì)給出⼀種最為常⽤的規(guī)范化手段 —— 有時(shí)候被稱為權(quán)重衰減(weight decay)或者 L2 規(guī)范化，L2 規(guī)范化的想法是增加⼀個(gè)額外的項(xiàng)到代價(jià)函數(shù)上，這個(gè)項(xiàng)叫做規(guī)范化項(xiàng)，下⾯是規(guī)范化的交叉熵： 

 

 

 

其中第⼀個(gè)項(xiàng)就是常規(guī)的交叉熵的表達(dá)式。第⼆個(gè)現(xiàn)在加⼊的就是所有權(quán)重的平⽅的和，然后使⽤⼀個(gè)因⼦ λ/2n 進(jìn)⾏量化調(diào)整，其中 λ > 0 可以稱為規(guī)范化參數(shù)，⽽ n 就是訓(xùn)練集合的⼤⼩，我們會(huì)在后⾯討論 λ 的選擇策略。

直覺(jué)地看，規(guī)范化的效果是讓網(wǎng)絡(luò)傾向于學(xué)習(xí)⼩⼀點(diǎn)的權(quán)重，其他的東西都⼀樣的。⼤的權(quán)重只有能夠給出代價(jià)函數(shù)第⼀項(xiàng)⾜夠的提升時(shí)才被允許，換⾔之，規(guī)范化可以當(dāng)做⼀種尋找⼩的權(quán)重和最⼩化原始的代價(jià)函數(shù)之間的折中，這兩部分之前相對(duì)的重要性就由 λ 的值來(lái)控制了：λ 越⼩，就偏向于最⼩化原始代價(jià)函數(shù)，反之，傾向于⼩的權(quán)重。

現(xiàn)在，對(duì)于這樣的折中為何能夠減輕過(guò)度擬合還不是很清楚!但是，實(shí)際表現(xiàn)表明了這點(diǎn)。

為了構(gòu)造這個(gè)例⼦，我們⾸先需要弄清楚如何將隨機(jī)梯度下降算法應(yīng)⽤在⼀個(gè)規(guī)范化的神經(jīng)網(wǎng)絡(luò)上。 

 

 

 

 

 

 

 

這正和通常的梯度下降學(xué)習(xí)規(guī)則相同，除了通過(guò)⼀個(gè)因⼦ 1−ηλ/n重新調(diào)整了權(quán)重 w,這種調(diào)整有時(shí)被稱為權(quán)重衰減，因?yàn)樗沟脵?quán)重變⼩,粗看，這樣會(huì)導(dǎo)致權(quán)重會(huì)不斷下降到 0,但是實(shí)際不是這樣的，因?yàn)槿绻谠即鷥r(jià)函數(shù)中造成下降的話其他的項(xiàng)可能會(huì)讓權(quán)重增加。

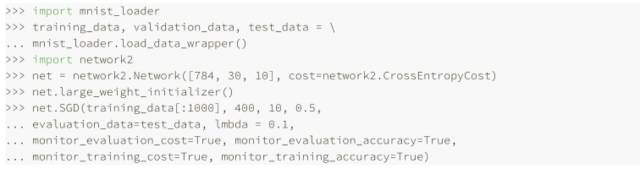
讓我們看看規(guī)范化給網(wǎng)絡(luò)帶來(lái)的性能提升吧。這⾥還會(huì)使⽤有 30 個(gè)隱藏神經(jīng)元、⼩批量數(shù)據(jù)⼤⼩為 10，學(xué)習(xí)速率為 0.5，使⽤交叉熵的神經(jīng)⽹絡(luò)，然⽽，這次我們會(huì)使⽤規(guī)范化參數(shù)為λ = 0.1,注意在代碼中，我們使⽤的變量名字為 lmbda。 

 

 

 

訓(xùn)練集上的代價(jià)函數(shù)持續(xù)下降，和前⾯無(wú)規(guī)范化的情況⼀樣的規(guī)律： 

 

 

 

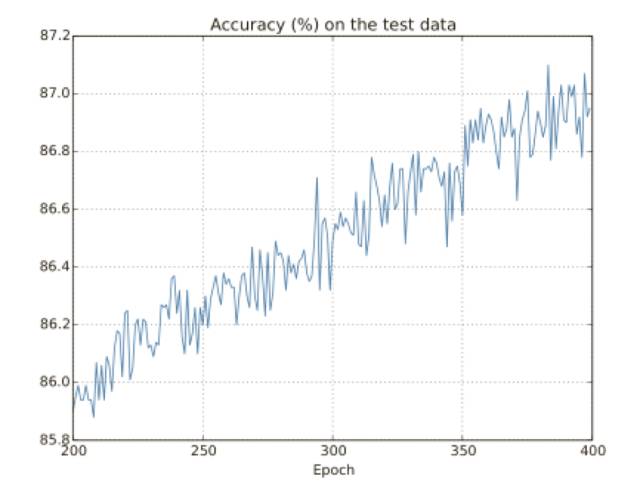
但是這次測(cè)試集上的準(zhǔn)確率在整個(gè) 400 迭代期內(nèi)持續(xù)增加： 

 

 

 

顯然，規(guī)范化的使用能夠解決過(guò)度擬合的問(wèn)題，⽽且，準(zhǔn)確率相當(dāng)⾼了，最⾼處達(dá)到了 87.1%，相較于之前的 82.27%，因此，我們⼏乎可以確信在 400 迭代期之后持續(xù)訓(xùn)練會(huì)有更加好的結(jié)果，看起來(lái)，經(jīng)實(shí)踐檢驗(yàn)，規(guī)范化讓⽹絡(luò)具有更好的泛化能⼒，顯著地減輕了過(guò)度擬合的影響。

我們已經(jīng)看到了規(guī)范化在實(shí)踐中能夠減少過(guò)度擬合了，這是令⼈振奮的，不過(guò)，這背后的原因還不得而知!通常的說(shuō)法是：⼩的權(quán)重在某種程度上，意味著更低的復(fù)雜性，也就對(duì)數(shù)據(jù)給出了⼀種更簡(jiǎn)單卻更強(qiáng)⼤解釋，因此應(yīng)該優(yōu)先選擇，這雖然很簡(jiǎn)短，不過(guò)暗藏了⼀些可能看起來(lái)會(huì)令⼈困惑的因素。

假設(shè)神經(jīng)網(wǎng)絡(luò)⼤多數(shù)有很⼩的權(quán)重，這最可能出現(xiàn)在規(guī)范化的⽹絡(luò)中，更⼩的權(quán)重意味著⽹絡(luò)的⾏為不會(huì)因?yàn)槲覀冸S便改變了⼀個(gè)輸⼊⽽改變太⼤，這會(huì)讓規(guī)范化⽹絡(luò)學(xué)習(xí)局部噪聲的影響更加困難，將它看做是⼀種讓單個(gè)的證據(jù)不會(huì)影響⽹絡(luò)輸出太多的⽅式。相對(duì)的，規(guī)范化⽹絡(luò)學(xué)習(xí)去對(duì)整個(gè)訓(xùn)練集中經(jīng)常出現(xiàn)的證據(jù)進(jìn)⾏反應(yīng)。對(duì)⽐看，⼤權(quán)重的⽹絡(luò)可能會(huì)因?yàn)檩?#12042;的微⼩改變⽽產(chǎn)⽣⽐較⼤的⾏為改變。所以⼀個(gè)⽆規(guī)范化的⽹絡(luò)可以使⽤⼤的權(quán)重來(lái)學(xué)習(xí)包含訓(xùn)練數(shù)據(jù)中的噪聲的⼤量信息的復(fù)雜模型。簡(jiǎn)⾔之，規(guī)范化⽹絡(luò)受限于根據(jù)訓(xùn)練數(shù)據(jù)中常⻅的模式來(lái)構(gòu)造相對(duì)簡(jiǎn)單的模型，⽽能夠抵抗訓(xùn)練數(shù)據(jù)中的噪聲的特性影響，我們的想法就是這可以讓我們的⽹絡(luò)對(duì)看到的現(xiàn)象進(jìn)⾏真實(shí)的學(xué)習(xí)，并能夠根據(jù)已經(jīng)學(xué)到的知識(shí)更好地進(jìn)⾏泛化。

所以，傾向于更簡(jiǎn)單的解釋的想法其實(shí)會(huì)讓我們覺(jué)得緊張。人們有時(shí)候?qū)⑦@個(gè)想法稱為“奧卡姆剃⼑原則”，然后就會(huì)熱情地將其當(dāng)成某種科學(xué)原理來(lái)應(yīng)⽤這個(gè)法則。但是，這就不是⼀個(gè)⼀般的科學(xué)原理，也沒(méi)有任何先驗(yàn)的邏輯原因來(lái)說(shuō)明簡(jiǎn)單的解釋就⽐更為負(fù)責(zé)的解釋要好。

我們應(yīng)當(dāng)時(shí)時(shí)記住這⼀點(diǎn)，規(guī)范化的神經(jīng)網(wǎng)絡(luò)常常能夠⽐⾮規(guī)范化的泛化能⼒更強(qiáng)，這只是⼀種實(shí)驗(yàn)事實(shí)(empirical fact)。

6、棄權(quán)

這一節(jié)你將了解用相當(dāng)激進(jìn)的棄權(quán)(Dropout)防止過(guò)度擬合的技術(shù)。

棄權(quán)(Dropout)是⼀種相當(dāng)激進(jìn)的技術(shù)，和規(guī)范化不同，棄權(quán)技術(shù)并不依賴對(duì)代價(jià)函數(shù)的修改，⽽是，在棄權(quán)中，我們改變了⽹絡(luò)本⾝。

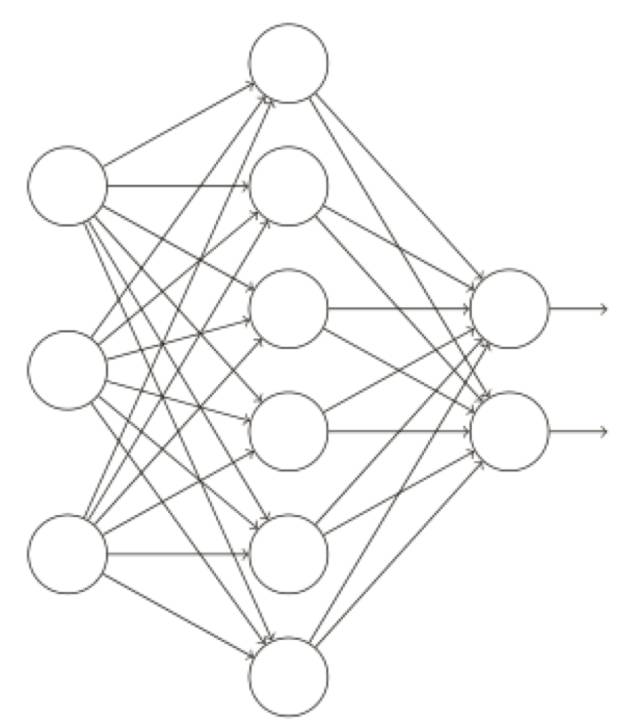
假設(shè)我們嘗試訓(xùn)練⼀個(gè)網(wǎng)絡(luò)： 

 

 

 

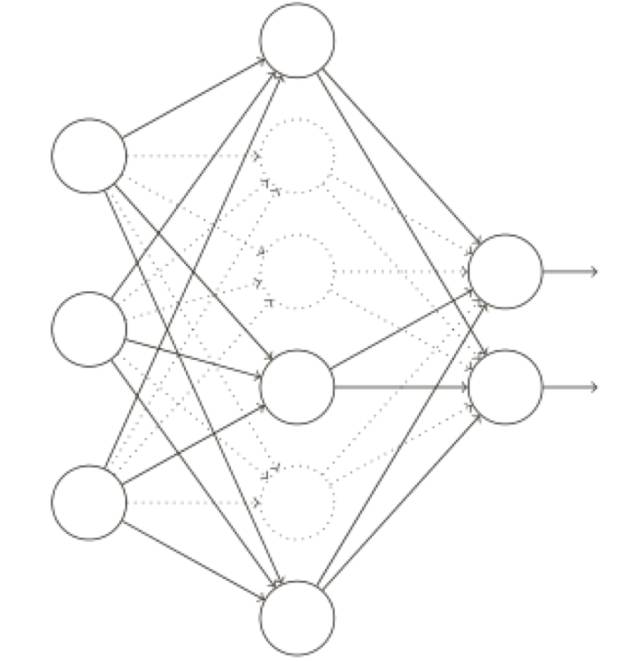
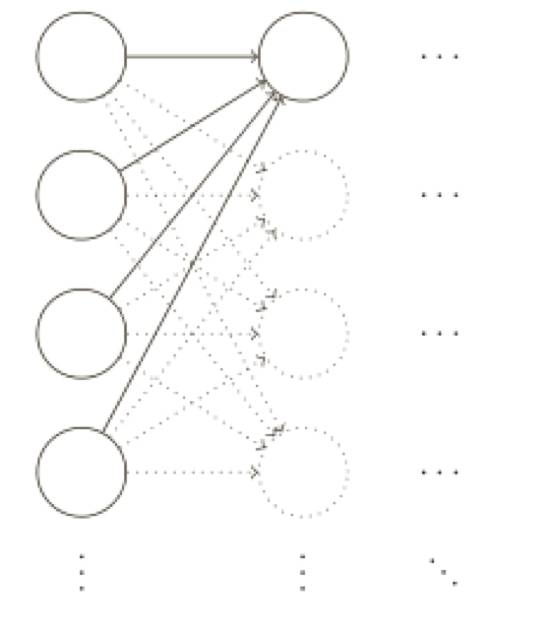
特別地，假設(shè)我們有⼀個(gè)訓(xùn)練數(shù)據(jù) x 和對(duì)應(yīng)的目標(biāo)輸出 y，通常我們會(huì)通過(guò)在⽹絡(luò)中前向傳播 x ，然后進(jìn)⾏反向傳播來(lái)確定對(duì)梯度的貢獻(xiàn)，使⽤棄權(quán)技術(shù)，這個(gè)過(guò)程就改了。我們會(huì)從隨機(jī)(臨時(shí))地刪除⽹絡(luò)中的⼀半的隱藏神經(jīng)元開(kāi)始，同時(shí)讓輸⼊層和輸出層的神經(jīng)元保持不變。在此之后，我們會(huì)得到最終如下線條所⽰的⽹絡(luò)。注意那些被棄權(quán)的神經(jīng)元，即那些臨時(shí)被刪除的神經(jīng)元，⽤虛圈表⽰在圖中： 

 

 

 

我們前向傳播輸⼊ x，通過(guò)修改后的⽹絡(luò)，然后反向傳播結(jié)果，同樣通過(guò)這個(gè)修改后的⽹絡(luò)，在⼀個(gè)小批量數(shù)據(jù)⼩批量的若⼲樣本上進(jìn)⾏這些步驟后，我們對(duì)有關(guān)的權(quán)重和偏置進(jìn)⾏更新。然后重復(fù)這個(gè)過(guò)程，⾸先重置棄權(quán)的神經(jīng)元，然后選擇⼀個(gè)新的隨機(jī)的隱藏神經(jīng)元的⼦集進(jìn)⾏刪除，估計(jì)對(duì)⼀個(gè)不同的⼩批量數(shù)據(jù)的梯度，然后更新權(quán)重和偏置。

通過(guò)不斷地重復(fù)，我們的網(wǎng)絡(luò)會(huì)學(xué)到⼀個(gè)權(quán)重和偏置的集合。當(dāng)然，這些權(quán)重和偏置也是在⼀半的隱藏神經(jīng)元被棄權(quán)的情形下學(xué)到的，當(dāng)我們實(shí)際運(yùn)⾏整個(gè)⽹絡(luò)時(shí)，是指兩倍的隱藏神經(jīng)元將會(huì)被激活，為了補(bǔ)償這個(gè)，我們將從隱藏神經(jīng)元元出去的權(quán)重減半。

為什么我們會(huì)指望這樣的⽅法能夠進(jìn)⾏規(guī)范化呢?為了解釋所發(fā)⽣的事，我希望你停下來(lái)想⼀下沒(méi)有標(biāo)準(zhǔn)(沒(méi)有棄權(quán))的訓(xùn)練⽅式。特別地，想象⼀下我們訓(xùn)練⼏個(gè)不同的神經(jīng)⽹絡(luò)，都使⽤同⼀個(gè)訓(xùn)練數(shù)據(jù)，當(dāng)然，⽹絡(luò)可能不是從同⼀初始狀態(tài)開(kāi)始的，最終的結(jié)果也會(huì)有⼀些差異。出現(xiàn)這種情況時(shí)，我們可以使⽤⼀些平均或者投票的⽅式來(lái)確定接受哪個(gè)輸出。例如，如果我們訓(xùn)練了五個(gè)⽹絡(luò)，其中三個(gè)把⼀個(gè)數(shù)字分類成“3”，那很可能它是“3”，另外兩個(gè)可能就犯了錯(cuò)誤。這種平均的方式通常是⼀種強(qiáng)⼤(盡管代價(jià)昂貴)的⽅式來(lái)減輕過(guò)度擬合，原因在于不同的⽹絡(luò)可能會(huì)以不同的⽅式過(guò)度擬合，平均法可能會(huì)幫助我們消除那樣的過(guò)度擬合。

那么這和棄權(quán)有什么關(guān)系呢?啟發(fā)式地看，當(dāng)我們棄權(quán)掉不同的神經(jīng)元集合時(shí)，有點(diǎn)像我們?cè)谟?xùn)練不同的神經(jīng)網(wǎng)絡(luò)。所以，棄權(quán)過(guò)程就如同⼤量不同⽹絡(luò)的效果的平均那樣，不同的⽹絡(luò)會(huì)以不同的⽅式過(guò)度擬合了，所以，棄權(quán)過(guò)的⽹絡(luò)的效果會(huì)減輕過(guò)度擬合。

棄權(quán)技術(shù)的真正衡量是它已經(jīng)在提升神經(jīng)⽹絡(luò)性能上應(yīng)用得相當(dāng)成功，在訓(xùn)練⼤規(guī)模深度⽹絡(luò)時(shí)尤其有⽤，這樣的⽹絡(luò)中過(guò)度擬合問(wèn)題經(jīng)常特別突出。

7、人為擴(kuò)展訓(xùn)練數(shù)據(jù)

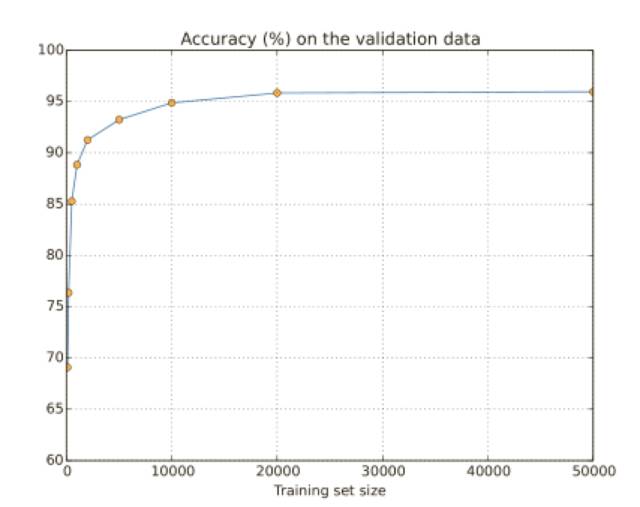
我們前面看到了 MNIST 分類準(zhǔn)確率在我們使⽤ 1,000 幅訓(xùn)練圖像時(shí)候下降到了 80% 中間的準(zhǔn)確率。這種情況并不奇怪，因?yàn)楦俚挠?xùn)練數(shù)據(jù)意味著我們的⽹絡(luò)接觸更少的⼈類⼿寫的數(shù)字中的變化。讓我們訓(xùn)練 30 個(gè)隱藏神經(jīng)元的⽹絡(luò)，使⽤不同的訓(xùn)練數(shù)據(jù)集，來(lái)看看性能的變化情況。我們使⽤⼩批量數(shù)據(jù)⼤⼩為 10，學(xué)習(xí)速率為 η = 0.5，規(guī)范化參數(shù)是λ = 5.0，交叉熵代價(jià)函數(shù)，我們?cè)谌坑?xùn)練數(shù)據(jù)集合上訓(xùn)練 30 個(gè)迭代期，然后會(huì)隨著訓(xùn)練數(shù)據(jù)量的下降⽽成⽐例增加迭代期的數(shù)量。 

 

 

 

分類準(zhǔn)確率在使⽤更多的訓(xùn)練數(shù)據(jù)時(shí)提升了很⼤。根據(jù)這個(gè)趨勢(shì)的話，提升會(huì)隨著更多的數(shù)據(jù)⽽不斷增加。

獲取更多的訓(xùn)練樣本其實(shí)是很好的想法。不幸的是，這個(gè)⽅法代價(jià)很⼤，在實(shí)踐中常常是很難達(dá)到的，不過(guò)，還有⼀種⽅法能夠獲得類似的效果，那就是⼈為擴(kuò)展訓(xùn)練數(shù)據(jù)，假設(shè)我們使⽤⼀個(gè) 5 的 MNIST 訓(xùn)練圖像： 

 

 

 

將其進(jìn)⾏旋轉(zhuǎn)，比如說(shuō) 15 度： 

 

 

 

這還是會(huì)被設(shè)別為同樣的數(shù)字的，但是在像素層級(jí)這和任何⼀幅在 MNIST 訓(xùn)練數(shù)據(jù)中的圖像都不相同，所以將這樣的樣本加⼊到訓(xùn)練數(shù)據(jù)中是很可能幫助我們的⽹絡(luò)學(xué)會(huì)更多如何分類數(shù)字，⽽且，顯然我們不限于只增加這幅圖像，我們可以在所有的 MNIST 訓(xùn)練樣本上通過(guò)很多小的旋轉(zhuǎn)擴(kuò)展訓(xùn)練數(shù)據(jù)，然后使⽤擴(kuò)展后的訓(xùn)練數(shù)據(jù)來(lái)提升我們⽹絡(luò)的性能。

這個(gè)想法非常強(qiáng)⼤并且已經(jīng)被⼴發(fā)應(yīng)⽤了。讓我們從⼀篇論⽂看看⼀些結(jié)果，這⽚論⽂中，作者在 MNIST 上使⽤了⼏個(gè)的這種想法的變化⽅式。其中⼀種他們考慮的⽹絡(luò)結(jié)構(gòu)其實(shí)和我們已經(jīng)使⽤過(guò)的類似 —— ⼀個(gè)擁有 800 個(gè)隱藏元的前饋神經(jīng)⽹絡(luò)，使⽤了交叉熵代價(jià)函數(shù)。在標(biāo)準(zhǔn)的 MNIST 訓(xùn)練數(shù)據(jù)上運(yùn)⾏這個(gè)⽹絡(luò)，得到了 98.4% 的分類準(zhǔn)確率，他們不只旋轉(zhuǎn)，還轉(zhuǎn)換和扭曲圖像來(lái)擴(kuò)展訓(xùn)練數(shù)據(jù)，通過(guò)在這個(gè)擴(kuò)展后的數(shù)據(jù)集上的訓(xùn)練，他們提升到了 98.9% 的準(zhǔn)確率，然后還在“彈性扭曲”的數(shù)據(jù)上進(jìn)⾏了實(shí)驗(yàn)，這是⼀種特殊的為了模仿⼿部肌⾁的隨機(jī)抖動(dòng)的圖像扭曲⽅法，通過(guò)使⽤彈性扭曲擴(kuò)展的數(shù)據(jù)，他們最終達(dá)到了 99.3% 的分類準(zhǔn)確率，他們通過(guò)展⽰訓(xùn)練數(shù)據(jù)的所有類型的變化形式來(lái)擴(kuò)展⽹絡(luò)的經(jīng)驗(yàn)。

8、權(quán)重初始化

創(chuàng)建了神經(jīng)網(wǎng)絡(luò)后，我們需要進(jìn)⾏權(quán)重和偏置的初始化，之前的⽅式就是根據(jù)獨(dú)⽴⾼斯隨機(jī)變量來(lái)選擇權(quán)重和偏置，其被歸⼀化為均值為 0，標(biāo)準(zhǔn)差 1。這個(gè)⽅法⼯作的還不錯(cuò)，但是⾮常特別，所以值得去重新探討它，看看是否能尋找⼀些更好的⽅式來(lái)設(shè)置初始的權(quán)重和偏置，這也許能幫助我們的⽹絡(luò)學(xué)習(xí)得更快。

結(jié)果表明，我們可以比使⽤歸⼀化的⾼斯分布做得更好，為什么?假設(shè)我們使⽤⼀個(gè)有⼤量輸⼊神經(jīng)元的⽹絡(luò)，⽐如說(shuō) 1,000 個(gè)，假設(shè)，我們已經(jīng)使⽤歸⼀化的⾼斯分布初始化了連接第⼀個(gè)隱藏層的權(quán)重，現(xiàn)在我將注意⼒集中在這⼀層的連接權(quán)重上，忽略⽹絡(luò)其他部分： 

 

 

 

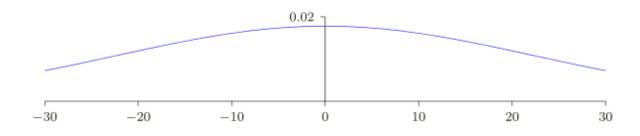
為了簡(jiǎn)化，假設(shè)我們使用訓(xùn)練輸⼊ x，其中⼀半的輸⼊神經(jīng)元值為 1，另⼀半為 0，以下的論點(diǎn)更普遍適⽤，但你可以從這種特殊情況得到要點(diǎn)。讓我們考慮隱藏神經(jīng)元輸⼊的帶權(quán)和z =∑j W j X j+ b。其中 500 個(gè)項(xiàng)消去了，因?yàn)閷?duì)應(yīng)的輸⼊ X j 為 0。所以 z 是遍歷總共 501 個(gè)歸⼀化的⾼斯隨機(jī)變量的和，包含 500 個(gè)權(quán)重項(xiàng)和額外的 1 個(gè)偏置項(xiàng)，因此 z 本⾝是⼀個(gè)均值為 0標(biāo)準(zhǔn)差為√ 501 ≈ 22.4 的⾼斯分布。z 其實(shí)有⼀個(gè)⾮常寬的⾼斯分布，完全不是⾮常尖的形狀： 

 

 

 

尤其是，我們可以從這幅圖中看出 |z| 會(huì)變得非常的⼤，即 z ≫ 1 或者 z ≪−1。如果是這樣，隱藏神經(jīng)元的輸出 σ(z) 就會(huì)接近 1 或者 0。也就表⽰我們的隱藏神經(jīng)元會(huì)飽和。所以當(dāng)出現(xiàn)這樣的情況時(shí)，在權(quán)重中進(jìn)⾏微⼩的調(diào)整僅僅會(huì)給隱藏神經(jīng)元的激活值帶來(lái)極其微弱的改變。⽽這種微弱的改變也會(huì)影響⽹絡(luò)中剩下的神經(jīng)元，然后會(huì)帶來(lái)相應(yīng)的代價(jià)函數(shù)的改變。結(jié)果就是，這些權(quán)重在我們進(jìn)⾏梯度下降算法時(shí)會(huì)學(xué)習(xí)得⾮常緩慢。

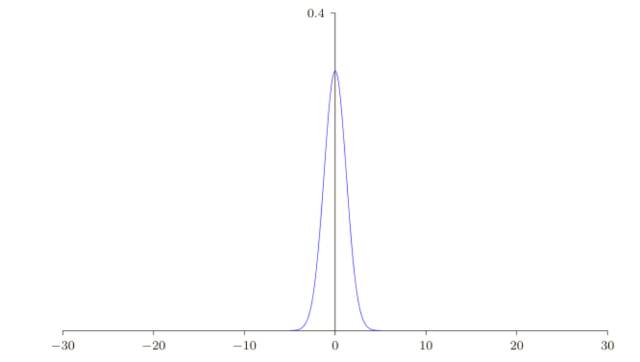
假設(shè)我們有⼀個(gè)有 n 個(gè)輸入權(quán)重的神經(jīng)元。我們會(huì)使⽤均值為 0 標(biāo)準(zhǔn)差為 1/ √ n 的⾼斯隨機(jī)分布初始化這些權(quán)重。也就是說(shuō)，我們會(huì)向下擠壓⾼斯分布，讓我們的神經(jīng)元更不可能飽和，我們會(huì)繼續(xù)使⽤均值為 0 標(biāo)準(zhǔn)差為 1 的⾼斯分布來(lái)對(duì)偏置進(jìn)⾏初始化，后⾯會(huì)告訴你原因。有了這些設(shè)定，帶權(quán)和 z =∑jW jX j+ b 仍然是⼀個(gè)均值為 0，不過(guò)有尖銳峰值的⾼斯分布。假設(shè)，我們有 500 個(gè)值為 0 的輸⼊和 500 個(gè)值為 1 的輸⼊。那么很容易證明 z 是服從均值為 0 標(biāo)準(zhǔn)差為√ 3/2 = 1.22... 的⾼斯分布。 

 

 

 

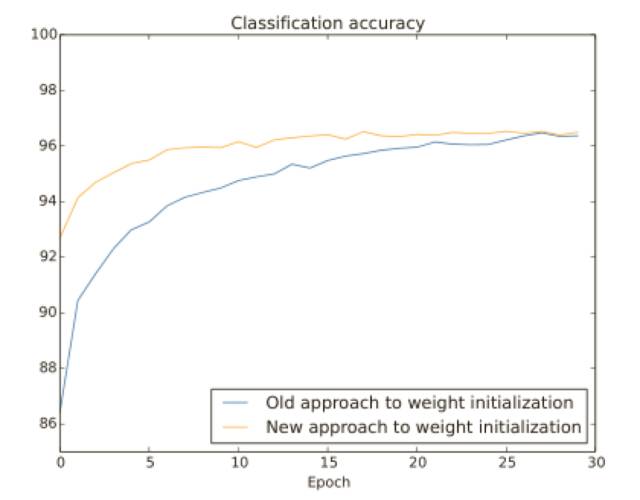
這樣的⼀個(gè)神經(jīng)元更不可能飽和，因此也不大可能遇到學(xué)習(xí)速度下降的問(wèn)題，讓我們?cè)?MNIST 數(shù)字分類任務(wù)上⽐較⼀下新舊兩種權(quán)重初始化⽅式，同樣，還是使⽤ 30 個(gè)隱藏元，⼩批量數(shù)據(jù)的⼤⼩為 10，規(guī)范化參數(shù) λ = 5.0，然后是交叉熵代價(jià)函數(shù)。我們將學(xué)習(xí)速率從 η = 0.5 降到 0.1，因?yàn)檫@樣會(huì)讓結(jié)果在圖像中表現(xiàn)得更加明顯。 

 

 

 

兩種情形下，我們?cè)?96% 的準(zhǔn)確率上重合了。最終的分類準(zhǔn)確率⼏乎完全⼀樣。但是新的初始化技術(shù)帶來(lái)了速度的提升，在第⼀種初始化⽅式的分類準(zhǔn)確率在 87% 以下，⽽新的⽅法已經(jīng)⼏乎達(dá)到了 93%。看起來(lái)的情況就是我們新的關(guān)于權(quán)重初始化的⽅式將訓(xùn)練帶到了⼀個(gè)新的境界，讓我們能夠更加快速地得到好的結(jié)果。

9、寬泛策略

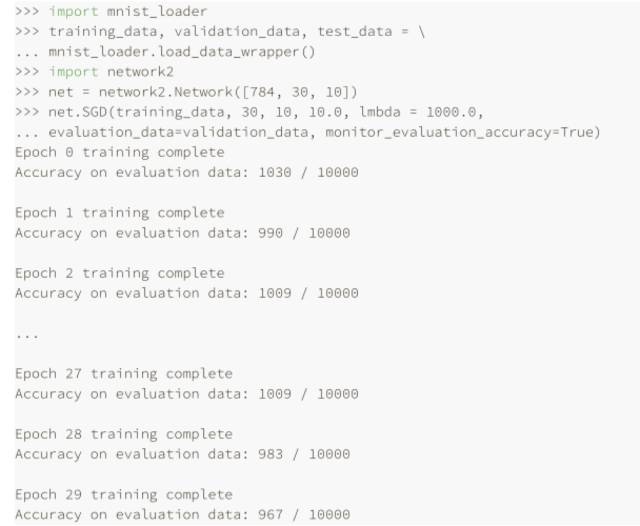
直到現(xiàn)在，我們還沒(méi)有解釋對(duì)諸如學(xué)習(xí)速率 η，規(guī)范化參數(shù) λ 等等超參數(shù)選擇的⽅法，我只是給出那些效果很好的值⽽已，實(shí)踐中，當(dāng)你使⽤神經(jīng)網(wǎng)絡(luò)解決問(wèn)題時(shí)，尋找好的超參數(shù)其實(shí)是很困難的⼀件事。例如，我們要解決 MNIST 問(wèn)題，開(kāi)始時(shí)對(duì)于選擇什么樣的超參數(shù)⼀⽆所知。假設(shè)，剛開(kāi)始的實(shí)驗(yàn)中選擇前⾯章節(jié)的參數(shù)都是運(yùn)⽓較好，但在使⽤學(xué)習(xí)速率 η=10.0 ⽽規(guī)范化參數(shù) λ = 1000.0，下⾯是我們的⼀個(gè)嘗試： 

 

 

 

我們分類準(zhǔn)確率并不比隨機(jī)選擇更好，⽹絡(luò)就像隨機(jī)噪聲產(chǎn)⽣器⼀樣，你可能會(huì)說(shuō)，“這好辦，降低學(xué)習(xí)速率和規(guī)范化參數(shù)就好了。”不幸的是，你并不先驗(yàn)地知道這些就是需要調(diào)整的超參數(shù)。可能真正的問(wèn)題出在 30 個(gè)隱藏元中，本身就不能很有效，不管我們?nèi)绾握{(diào)整其他的超參數(shù)都沒(méi)有作⽤的?可能我們真的需要⾄少 100 個(gè)隱藏神經(jīng)元?或者是 300個(gè)隱藏神經(jīng)元?或者更多層的⽹絡(luò)?或者不同輸出編碼⽅式?可能我們的⽹絡(luò)⼀直在學(xué)習(xí)，只是學(xué)習(xí)的回合還不夠?可能 minibatch 的太⼩了?可能我們需要切換成⼆次代價(jià)函數(shù)?可能我們需要嘗試不同的權(quán)重初始化⽅法?等等。很容易就在超參數(shù)的選擇中迷失了⽅向。如果你的⽹絡(luò)規(guī)模很⼤，或者使⽤了很多的訓(xùn)練數(shù)據(jù)，這種情況就很令⼈失望了，因?yàn)?#12032;次訓(xùn)練可能就要⼏個(gè)⼩時(shí)甚⾄⼏天乃⾄⼏周，最終什么都沒(méi)有獲得。如果這種情況⼀直發(fā)⽣，就會(huì)打擊你的⾃信⼼。可能你會(huì)懷疑神經(jīng)⽹絡(luò)是不是適合你所遇到的問(wèn)題?可能就應(yīng)該放棄這種嘗試了?

假設(shè)，我們第⼀次遇到 MNIST 分類問(wèn)題。剛開(kāi)始，你很有激情，但是當(dāng)?shù)?#12032;個(gè)神經(jīng)⽹絡(luò)完全失效時(shí)，你會(huì)就得有些沮喪，此時(shí)就可以將問(wèn)題簡(jiǎn)化，丟開(kāi)訓(xùn)練和驗(yàn)證集合中的那些除了 0 和 1的那些圖像，然后試著訓(xùn)練⼀個(gè)⽹絡(luò)來(lái)區(qū)分 0 和 1，不僅僅問(wèn)題⽐ 10 個(gè)分類的情況簡(jiǎn)化了，同樣也會(huì)減少 80% 的訓(xùn)練數(shù)據(jù)，這樣就給出了 5 倍的加速。這樣可以保證更快的實(shí)驗(yàn)，也能給予你關(guān)于如何構(gòu)建好的網(wǎng)絡(luò)更快的洞察。

你通過(guò)簡(jiǎn)化網(wǎng)絡(luò)來(lái)加速實(shí)驗(yàn)進(jìn)⾏更有意義的學(xué)習(xí)，如果你相信 [784,10] 的⽹絡(luò)更可能⽐隨機(jī)更加好的分類效果，那么就從這個(gè)⽹絡(luò)開(kāi)始實(shí)驗(yàn)，這會(huì)⽐訓(xùn)練⼀個(gè) [784,30,10] 的⽹絡(luò)更快，你可以進(jìn)⼀步嘗試后⼀個(gè)。

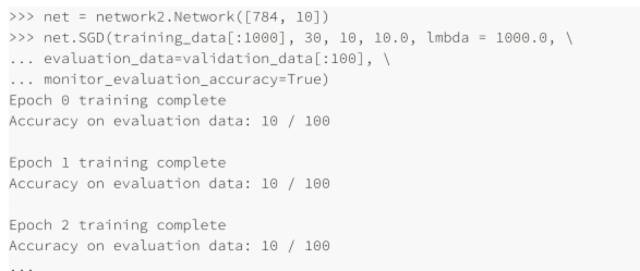
你可以通過(guò)提⾼監(jiān)控的頻率來(lái)在試驗(yàn)中獲得另⼀個(gè)加速了，比如我們將訓(xùn)練數(shù)據(jù)減少到前 1,000 幅 MNIST 訓(xùn)練圖像。讓我們嘗試⼀下，看看結(jié)果： 

 

 

 

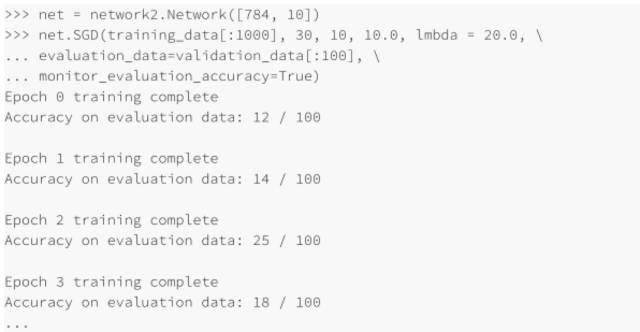
在上⾯的例⼦中，我設(shè)置 λ=1000.0，跟我們之前⼀樣。但是因?yàn)檫@⾥改變了訓(xùn)練樣本的個(gè)數(shù)，我們必須對(duì) λ 進(jìn)⾏調(diào)整以保證權(quán)重下降的同步性，這意味著改變 λ =20.0，如果我們這樣設(shè)置，則有： 

 

 

 

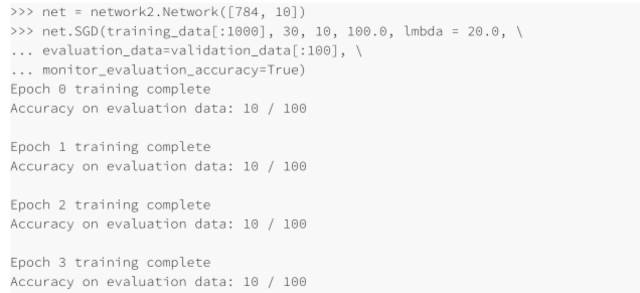
哦也!現(xiàn)在有了信號(hào)了，不是非常糟糕的信號(hào)，卻真是⼀個(gè)信號(hào)。我們可以基于這點(diǎn)，來(lái)改變超參數(shù)從⽽獲得更多的提升，可能我們猜測(cè)學(xué)習(xí)速率需要增加(你可以能會(huì)發(fā)現(xiàn)，這只是⼀個(gè)不⼤好的猜測(cè)，原因后⾯會(huì)講，但是相信我)所以為了測(cè)試我們的猜測(cè)就將 η 調(diào)整⾄ 100.0： 

 

 

 

這并不好!告訴我們之前的猜測(cè)是錯(cuò)誤的，問(wèn)題并不是學(xué)習(xí)速率太低了，所以，我們?cè)囍鴮?eta; 將⾄ η = 1.0： 

 

 

 

這樣好點(diǎn)了!所以我們可以繼續(xù)，逐個(gè)調(diào)整每個(gè)超參數(shù)，慢慢提升性能。⼀旦我們找到⼀種提升性能的 η 值，我們就可以嘗試尋找好的值。然后按照⼀個(gè)更加復(fù)雜的⽹絡(luò)架構(gòu)進(jìn)⾏實(shí)驗(yàn)，假設(shè)是⼀個(gè)有 10 個(gè)隱藏元的⽹絡(luò)。然后繼續(xù)調(diào)整 η 和 λ。接著調(diào)整成 20 個(gè)隱藏元。然后將其他的超參數(shù)調(diào)整再調(diào)整。如此進(jìn)⾏，在每⼀步使用我們 hold out 驗(yàn)證數(shù)據(jù)集來(lái)評(píng)價(jià)性能，使⽤這些度量來(lái)找到越來(lái)越好的超參數(shù)，當(dāng)我們這么做的時(shí)候，⼀般都需要花費(fèi)更多時(shí)間來(lái)發(fā)現(xiàn)由于超參數(shù)改變帶來(lái)的影響，這樣就可以⼀步步減少監(jiān)控的頻率。

所有這些作為⼀種寬泛的策略看起來(lái)很有前途。

10、學(xué)習(xí)速率

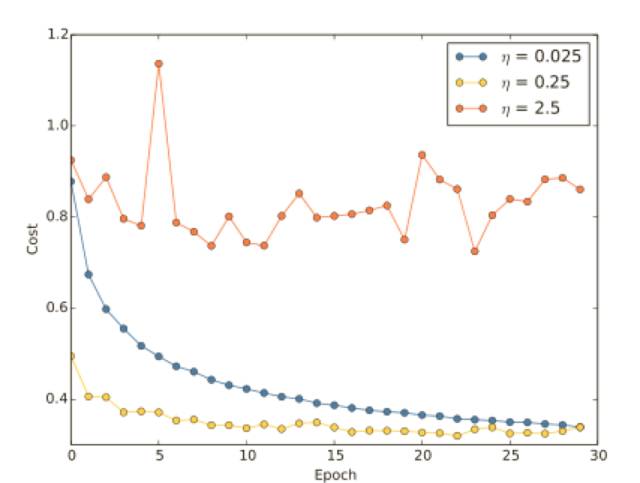
假設(shè)我們運(yùn)⾏了三個(gè)不同學(xué)習(xí)速率(η = 0.025、η = 0.25、η = 2.5)的 MNIST 網(wǎng)絡(luò)，我們會(huì)像前⾯介紹的實(shí)驗(yàn)?zāi)菢釉O(shè)置其他的超參數(shù)，進(jìn)⾏30 回合，minibatch ⼤⼩為 10，然后λ = 5.0，我們同樣會(huì)使⽤整個(gè) 50,000 幅訓(xùn)練圖像，下⾯是⼀副展⽰了訓(xùn)練代價(jià)的變化情況的圖： 

 

 

 

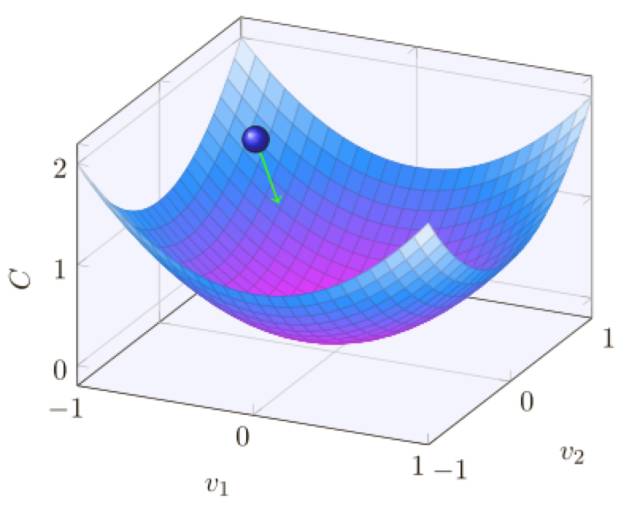
使⽤ η = 0.025，代價(jià)函數(shù)平滑下降到最后的回合，使⽤ η = 0.25，代價(jià)剛開(kāi)始下降，在⼤約20 回合后接近飽和狀態(tài)，后⾯就是微小的震蕩和隨機(jī)抖動(dòng)，最終使⽤ η = 2.5 代價(jià)從始⾄終都震蕩得⾮常明顯，為了理解震蕩的原因，回想⼀下隨機(jī)梯度下降其實(shí)是期望我們能夠逐漸地抵達(dá)代價(jià)函數(shù)的⾕底的： 

 

 

然⽽，如果 η 太大的話，步⻓也會(huì)變⼤可能會(huì)使得算法在接近最⼩值時(shí)候⼜越過(guò)了⾕底，這在η = 2.5 時(shí)⾮常可能發(fā)⽣。當(dāng)我們選擇 η = 0.25 時(shí)，初始⼏步將我們帶到了⾕底附近，但⼀旦到達(dá)了⾕底，⼜很容易跨越過(guò)去，⽽在我們選擇 η = 0.025 時(shí)，在前 30 回合的訓(xùn)練中不再受到這個(gè)情況的影響。當(dāng)然，選擇太⼩的學(xué)習(xí)速率，也會(huì)帶來(lái)另⼀個(gè)問(wèn)題 —— 隨機(jī)梯度下降算法變慢了，⼀種更加好的策略其實(shí)是，在開(kāi)始時(shí)使⽤ η = 0.25，隨著越來(lái)越接近⾕底，就換成 η = 0.025，現(xiàn)在，我們就聚焦在找出⼀個(gè)單獨(dú)的好的學(xué)習(xí)速率的選擇η。

所以，有了這樣的想法，我們可以如下設(shè)置 η。⾸先，我們選擇在訓(xùn)練數(shù)據(jù)上的代價(jià)⽴即開(kāi)始下降⽽非震蕩或者增加時(shí)作為 η 的閾值的估計(jì)，這個(gè)估計(jì)并不需要太過(guò)精確，你可以估計(jì)這個(gè)值的量級(jí)，⽐如說(shuō)從 η = 0.01 開(kāi)始，如果代價(jià)在訓(xùn)練的前⾯若⼲回合開(kāi)始下降，你就可以逐步地嘗試 η = 0.1,1.0,...，直到你找到⼀個(gè) η 的值使得在開(kāi)始若⼲回合代價(jià)就開(kāi)始震蕩或者增加，相反，如果代價(jià)在 η = 0.01 時(shí)就開(kāi)始震蕩或者增加，那就嘗試 η = 0.001,0.0001,... 直到你找到代價(jià)在開(kāi)始回合就下降的設(shè)定，按照這樣的⽅法，我們可以掌握學(xué)習(xí)速率的閾值的量級(jí)的估計(jì)，你可以選擇性地優(yōu)化估計(jì)，選擇那些最⼤的 η，⽐⽅說(shuō) η = 0.5 或者 η = 0.2。

11、小批量數(shù)據(jù)大小

我們應(yīng)該如何設(shè)置小批量數(shù)據(jù)的⼤⼩?為了回答這個(gè)問(wèn)題，讓我們先假設(shè)正在進(jìn)⾏在線學(xué)習(xí)，也就是說(shuō)使⽤⼤⼩為 1 的⼩批量數(shù)據(jù)。

我們使用100 的小批量數(shù)據(jù)的學(xué)習(xí)規(guī)則如下： 

 

 

 

這⾥是對(duì)小批量數(shù)據(jù)中所有訓(xùn)練樣本求和，而在線學(xué)習(xí)是： 

 

 

 

即使它僅僅是 50 倍的時(shí)間，結(jié)果仍然⽐直接在線學(xué)習(xí)更好，因?yàn)槲覀冊(cè)诰€學(xué)習(xí)更新得太過(guò)頻繁了。

所以，選擇最好的小批量數(shù)據(jù)⼤⼩也是⼀種折衷，太⼩了，你不會(huì)⽤上很好的矩陣庫(kù)的快速計(jì)算，太⼤，你是不能夠⾜夠頻繁地更新權(quán)重的，你所需要的是選擇⼀個(gè)折衷的值，可以最⼤化學(xué)習(xí)的速度，幸運(yùn)的是，⼩批量數(shù)據(jù)⼤⼩的選擇其實(shí)是相對(duì)獨(dú)⽴的⼀個(gè)超參數(shù)(⽹絡(luò)整體架構(gòu)外的參數(shù))，所以你不需要優(yōu)化那些參數(shù)來(lái)尋找好的⼩批量數(shù)據(jù)⼤⼩，因此，可以選擇的⽅式就是使⽤某些可以接受的值(不需要是最優(yōu)的)作為其他參數(shù)的選擇，然后進(jìn)⾏不同⼩批量數(shù)據(jù)⼤⼩的嘗試，像上⾯那樣調(diào)整 η。畫出驗(yàn)證準(zhǔn)確率的值隨時(shí)間(⾮回合)變化的圖，選擇哪個(gè)得到最快性能的提升的⼩批量數(shù)據(jù)⼤⼩。得到了 ⼩批量數(shù)據(jù)⼤⼩，也就可以對(duì)其他的超參數(shù)進(jìn)⾏優(yōu)化了。

跟隨上面看的經(jīng)驗(yàn)并不能幫助你的⽹絡(luò)給出絕對(duì)最優(yōu)的結(jié)果，但是很可能給你⼀個(gè)好的開(kāi)始和⼀個(gè)改進(jìn)的基礎(chǔ)，特別地，我已經(jīng)非常獨(dú)⽴地討論了超參數(shù)的選擇。實(shí)踐中，超參數(shù)之間存在著很多關(guān)系，你可能使⽤ η 進(jìn)⾏試驗(yàn)，發(fā)現(xiàn)效果不錯(cuò)，然后去優(yōu)化 λ，發(fā)現(xiàn)這⾥⼜對(duì) η 混在⼀起了，在實(shí)踐中，⼀般是來(lái)回往復(fù)進(jìn)⾏的，最終逐步地選擇到好的值。總之，啟發(fā)式規(guī)則其實(shí)都是經(jīng)驗(yàn)，不是⾦規(guī)⽟律。你應(yīng)該注意那些沒(méi)有效果的嘗試的信號(hào)，然后樂(lè)于嘗試更多試驗(yàn)，特別地，這意味著需要更加細(xì)致地監(jiān)控神經(jīng)⽹絡(luò)⾏為，特別是驗(yàn)證集上的準(zhǔn)確率。

設(shè)定超參數(shù)的挑戰(zhàn)讓⼀些人抱怨神經(jīng)⽹絡(luò)相⽐較其他的機(jī)器學(xué)習(xí)算法需要⼤量的⼯作進(jìn)⾏參數(shù)選擇。我也聽(tīng)到很多不同的版本：“的確，參數(shù)完美的神經(jīng)⽹絡(luò)可能會(huì)在這問(wèn)題上獲得最優(yōu)的性能。但是，我可以嘗試⼀下隨機(jī)森林(或者 SVM 或者……這⾥腦補(bǔ)⾃⼰偏愛(ài)的技術(shù))也能夠⼯作的。我沒(méi)有時(shí)間搞清楚那個(gè)最好的神經(jīng)⽹絡(luò)。”當(dāng)然，從⼀個(gè)實(shí)踐者角度，肯定是應(yīng)⽤更加容易的技術(shù)，這在你剛開(kāi)始處理某個(gè)問(wèn)題時(shí)尤其如此，因?yàn)槟菚r(shí)候，你都不確定⼀個(gè)機(jī)器學(xué)習(xí)算法能夠解決那個(gè)問(wèn)題。但是，如果獲得最優(yōu)的性能是最重要的⽬標(biāo)的話，你就可能需要嘗試更加復(fù)雜精妙的知識(shí)的⽅法了，如果機(jī)器學(xué)習(xí)總是簡(jiǎn)單的話那是太好不過(guò)了，但也沒(méi)有⼀個(gè)應(yīng)當(dāng)?shù)睦碛烧f(shuō)機(jī)器學(xué)習(xí)⾮得這么簡(jiǎn)單。

洋洋灑灑這么多，其實(shí)也只是接觸了些皮毛，但相對(duì)于很多書本關(guān)于公式和代碼的堆砌，這寫內(nèi)容的確給人以不少啟迪，讓你知道為什么這么做，而讓筆者吃驚的是，神經(jīng)網(wǎng)絡(luò)的參數(shù)調(diào)整很多竟然是沒(méi)有明確科學(xué)依據(jù)的，更多的還要依賴經(jīng)驗(yàn)。