[[191744]]

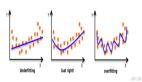
批歸一化技術(Batch Normalization)是深度學習中最近出現(xiàn)的一個有效的技術，已經(jīng)被廣泛證明其有效性，并很快應用于研究和應用中去。這篇文章假設讀者知道什么是批歸一化，并對批歸一化有一定程度的了解，知道它是如何工作的。如果你是剛剛接觸這個概念，或者需要復習一下，您可以在后面的鏈接地址找到批歸一化的簡要概述(http://blog.csdn.net/malefactor/article/details/51476961)。

本文使用兩種不同方法實現(xiàn)了一種神經(jīng)網(wǎng)絡。每一步都輸入相同的數(shù)據(jù)。網(wǎng)絡具有完全相同的損失函數(shù)、完全相同的超參數(shù)和完全相同的優(yōu)化器。然后在完全相同數(shù)量的 GPU 上進行訓練。結果是其中一個版本的分類準確度比另一種低2%，并且這種性能的下降表現(xiàn)地很穩(wěn)定。

我們拿一個簡單的 MNIST 和 SVHN 的分類問題為例。

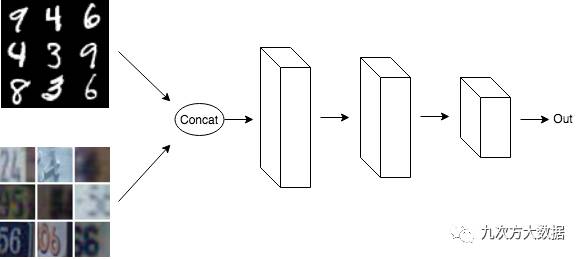
在***種實現(xiàn)中，抽取一批 MNIST 數(shù)據(jù)和一批 SVHN 數(shù)據(jù)，將它們合并到一起，然后將其輸入網(wǎng)絡。

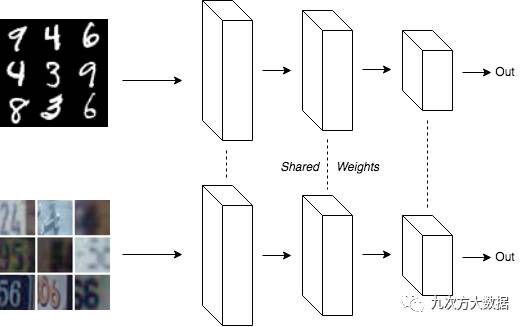
在第二種實現(xiàn)中，創(chuàng)建兩個副本的網(wǎng)絡，并共享權重。一個副本輸入 MNIST 數(shù)據(jù)，另一個副本輸入 SVHN 數(shù)據(jù)。

請注意，在這兩種實現(xiàn)里，一半的數(shù)據(jù)是 MNIST，另一半是 SVHN。另外由于第二種實現(xiàn)共享權重，使得兩個模型的參數(shù)數(shù)量相同，且其更新方式也相同。

簡單地想一下，這兩個模型的訓練過程中梯度應該是相同的。事實也是如此。但是在加入批歸一化之后情況就不同了。在***種實現(xiàn)中，同一批數(shù)據(jù)中同時包含 MNIST 數(shù)據(jù)和 SVHN 數(shù)據(jù)。而在第二種方法中，該模型分兩批進行訓練，一批只訓練 MNIST 數(shù)據(jù)，另一批只訓練 SVHN 數(shù)據(jù)。

導致這個問題的原因就是：在訓練的時候，在兩個網(wǎng)絡共享參數(shù)的同時，其數(shù)據(jù)集均值和方差的移動平均也是被共享的。這個參數(shù)的更新也是應用在兩套數(shù)據(jù)集上的。在第二種方法中，圖中上方的網(wǎng)絡用來自 MNIST 數(shù)據(jù)的平均值和方差的估計值進行訓練，而下方的網(wǎng)絡用 SVHN 數(shù)據(jù)平均值和方差的估計值進行訓練。但是由于移動平均在兩個網(wǎng)絡之間共享，所以移動平均收斂到 MNIST 和 SVHN 數(shù)據(jù)的平均值。

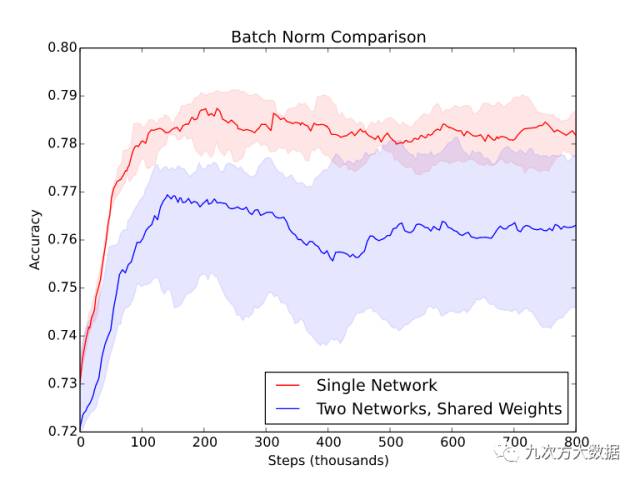
因此，在測試時，測試集使用的批歸一化的縮放和平移(某一種數(shù)據(jù)集的平均值)與模型預期的(兩種數(shù)據(jù)集的平均值)是不同的。當測試的歸一化與訓練的歸一化不同時，模型會得到如下結果。

該圖是在另一個相似數(shù)據(jù)集上(不是例子中的 MNIST 或 SVHN)用五個隨機種子的得到的***、中間和最差的模型的性能。當使用兩個共享權重的網(wǎng)絡時，不僅性能下降明顯，而且輸出結果的方差也增加。

每當單個小批次(minibatch)的數(shù)據(jù)不能代表整個數(shù)據(jù)的分布時，都會遇到這樣的問題。這就意味著忘記將輸入隨機打亂順序的情況下使用批歸一化是很危險的。這在最近流行的生成對抗網(wǎng)絡(GAN)里也是非常重要的。GAN中的判別器通常是對假數(shù)據(jù)和真實數(shù)據(jù)的混合進行訓練。如果在判別器中使用了批歸一化，在純假數(shù)據(jù)的批次或純真實數(shù)據(jù)批次之間進行交替是不正確的。每個小批次需要是兩者的均勻混合(各 50%)。

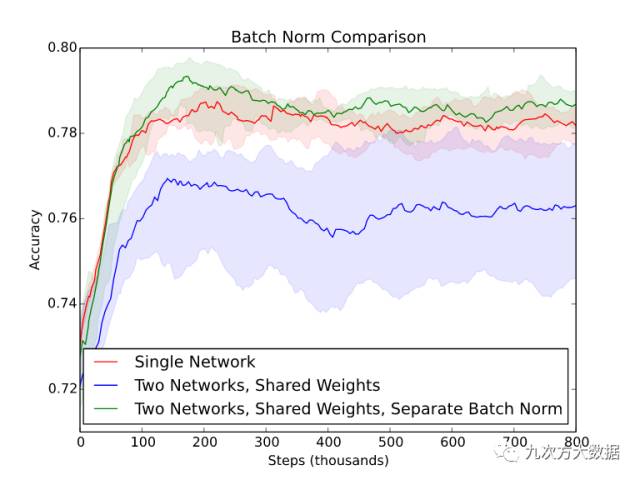
值得一提的是，在實踐中，使用分離批歸一化變量而共享其他變量的網(wǎng)絡結構得到了***的結果。雖然這樣實現(xiàn)起來比較復雜，但的確是比其他方法有效的(見下圖)。

批歸一化:萬惡之源 

縱觀上述問題，作者得出了能不用就不用批歸一化的結論。

這個結論是從工程的角度來分析的。

大體來講，當代碼出問題的時候，原因往往不外乎下面兩個:

1. 很明顯的錯誤。比如變量名輸錯了，或忘記調用某個函數(shù)。
2. 代碼對與其交互的其他代碼的行為有沒有寫明的依賴條件，并且的確有些條件沒有滿足。這些錯誤往往更加有害，因為一般需要花很長時間來弄清楚代碼依賴什么樣的條件。

這兩個錯誤都是不可避免的。第二類錯誤可以依靠使用更簡單的方法和重用已有代碼來減少。

批歸一化的方法有兩個基本的性質：

1. 在訓練時，單個輸入 xi 的輸出受制于小批次中的其他 xj 。
2. 在測試時，模型的計算路徑發(fā)生了變化。因為現(xiàn)在它使用移動平均值而不是小批次平均值來進行歸一化。

幾乎沒有其他優(yōu)化方法有這些性質。這樣的話，對于實現(xiàn)批歸一化代碼的人，很容易假設以下的前提：輸入的小批次內是不相關的，或者訓練時與測試時做的事情是一樣的。沒有人會質疑這種做法。

當然，你可以將批歸一化看作***歸一化黑盒，而且還挺好用的。但是在實踐中，抽象泄漏總是存在的，批歸一化也不例外，而且其特性使它更容易泄漏。

為什么大家還不放棄批歸一化? 

計算機學界有一封著名的文章： Dijkstra 的“ GoTo 語句是有害的”。在其中，Dijkstra 認為應該避免使用 goto 語句，因為它使得代碼更難閱讀，任何使用 goto 的程序都可以換種不用 goto 語句的方法重寫。

作者想要聲明“批歸一化是有害的”的觀點，但無奈找不到太好的理由，畢竟批歸一化實在太有用了。

沒錯，批歸一化的確存在問題。但當你做的一切都正確時，模型的確訓練地快的多。批歸一化的論文有超過 1400 次的引用不是白來的。

批歸一化有很多的替代方法，但它們也有自己的不足。層歸一化(Layer Normalization)與 RNN 合用才更有效，而且用于卷積層有時會有問題。權重歸一化(Weight Normalization)和余弦歸一化(Cosine Normalization)都是比較新型的歸一化方法。權重歸一化文章中表示，權重歸一化能夠適用于一些批歸一化不起作用的問題上。但是這些方法迄今為止并沒有太多應用，或許這只是個時間問題。層歸一化，權重歸一化和余弦歸一化都解決了上述批歸一化的問題。如果你在做一個新問題而且想冒點險的話，推薦試一下這些歸一化方法。畢竟不論用哪一種方法，都需要做超參數(shù)調整。調整好后，各種方法之間的區(qū)別應該是不大的。

(如果你足夠勇敢的話，甚至可以嘗試批重歸一化(Batch Renormalization)，不過它仍然只在測試時使用移動平均值。 )

使用批歸一化可以看作是深度學習中的“魔鬼的契約”。換來的是高效的訓練，失去的是可能的不正常的結果(insanity)。每個人都在簽著這個契約。

譯者注

作者關于”批歸一化是有害的“，以及“盡可能不使用批歸一化”的觀點不免有些偏激。但文中提到的批歸一化的陷阱的確是不得不防的。因為批歸一化的有效性，很多深度學習的研究者的確將其當作是“魔法黑箱”，將其應用到每一個可以用的地方。因為這種簡單粗暴的方法對于訓練速度的提高是很有效的。但大家很難將準確率的降低歸咎于批歸一化，畢竟從沒有見人提到過批歸一化會降低訓練準確率。

但這種訓練測試時數(shù)據(jù)集不一致的情況的確是很常見的。譯者做的人工模擬訓練數(shù)據(jù)集的方法中就會遇到這種問題。建議大家在使用批歸一化之前仔細考慮這樣幾個問題：

1. 我的訓練數(shù)據(jù)集的每批樣本是否平均?
2. 我的訓練數(shù)據(jù)集的每批均值是否和測試時的移動平均一致?

否則的話，就有必要使用下面中的一種或幾種方法來避免文中的問題：

1. 隨機采樣訓練數(shù)據(jù)集來確保批次平均;
2. 像文中的例子一樣修改模型來避免上述問題;
3. 使用層歸一化，權重歸一化或者余弦歸一化來替代批歸一化;
4. 不使用歸一化方法。