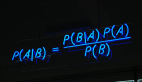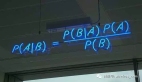相對于「 基于詞典的分析 」，「 基于機器學習 」的就不需要大量標注的詞典，但是需要大量標記的數據，比如：

還是下面這句話，如果它的標簽是：

服務質量 - 中 （共有三個級別，好、中、差）

╮(╯-╰)╭，其是機器學習，通過大量已經標簽的數據訓練出一個模型，

然后你在輸入一條評論，來判斷標簽級別

寧馨的點評 國慶活動，用62開頭的信用卡可以6.2元買一個印有銀聯卡標記的冰淇淋，
有香草，巧克力和抹茶三種口味可選，我選的是香草口味，味道很濃郁。
另外任意消費都可以10元買兩個馬卡龍，個頭雖不是很大，但很好吃，不是很甜的那種，不會覺得膩。
標簽：服務質量 - 中

  樸素貝葉斯

1、貝葉斯定理

假設對于某個數據集，隨機變量C表示樣本為C類的概率，F1表示測試樣本某特征出現的概率，套用基本貝葉斯公式，則如下所示：

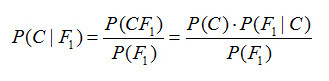
上式表示對于某個樣本，特征F1出現時，該樣本被分為C類的條件概率。那么如何用上式來對測試樣本分類呢？

舉例來說，有個測試樣本，其特征F1出現了（F1=1），那么就計算P(C=0|F1=1)和P(C=1|F1=1)的概率值。前者大，則該樣本被認為是0類；后者大，則分為1類。

對該公示，有幾個概念需要熟知：

先驗概率（Prior）。P(C)是C的先驗概率，可以從已有的訓練集中計算分為C類的樣本占所有樣本的比重得出。

證據（Evidence）。即上式P(F1)，表示對于某測試樣本，特征F1出現的概率。同樣可以從訓練集中F1特征對應樣本所占總樣本的比例得出。

似然（likelihood）。即上式P(F1|C)，表示如果知道一個樣本分為C類，那么他的特征為F1的概率是多少。

對于多個特征而言，貝葉斯公式可以擴展如下：

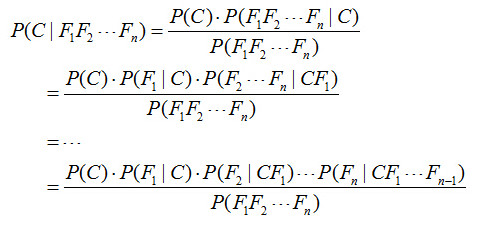
分子中存在一大串似然值。當特征很多的時候，這些似然值的計算是極其痛苦的。現在該怎么辦？

2、樸素的概念

為了簡化計算，樸素貝葉斯算法做了一假設：“樸素的認為各個特征相互獨立”。這么一來，上式的分子就簡化成了：

P(C)P(F1|C)P(F2|C)...P(Fn|C)。

這樣簡化過后，計算起來就方便多了。

這個假設是認為各個特征之間是獨立的，看上去確實是個很不科學的假設。因為很多情況下，各個特征之間是緊密聯系的。然而在樸素貝葉斯的大量應用實踐實際表明其工作的相當好。

其次，由于樸素貝葉斯的工作原理是計算P(C=0|F1...Fn)和P(C=1|F1...Fn)，并取最大值的那個作為其分類。而二者的分母是一模一樣的。因此，我們又可以省略分母計算，從而進一步簡化計算過程。

另外，貝葉斯公式推導能夠成立有個重要前期，就是各個證據（evidence）不能為0。也即對于任意特征Fx，P(Fx)不能為0。而顯示某些特征未出現在測試集中的情況是可以發生的。因此實現上通常要做一些小的處理，例如把所有計數進行+1（加法平滑 additive smoothing，又叫拉普拉斯平滑 Laplace smothing）。而如果通過增加一個大于 0 的可調參數 alpha 進行平滑，就叫 Lidstone 平滑。

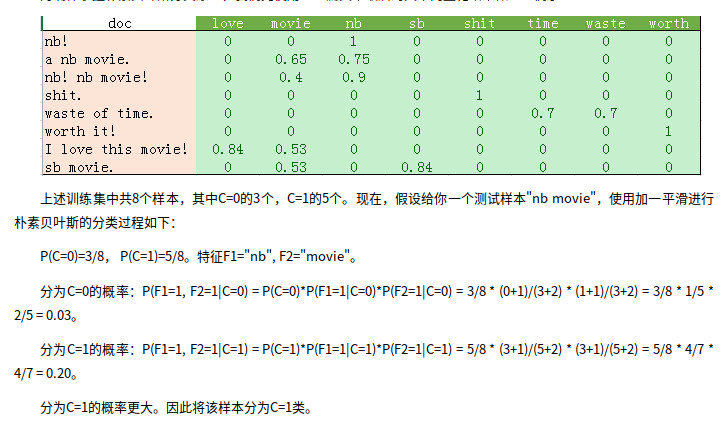
  基于樸素貝葉斯的情感分類

原始數據集，只抽了10條

讀數據

讀取excel文件，用的pandas庫的DataFrame的數據類型

分詞

對每個評論分詞，分詞的同時去除停用詞，得到如下詞表

每個列表是與評論一一對應的

統計

這里統計什么呢？統計兩種數據

1. 評論級別的次數

這里有三個級別分別對應
c0 → 好 2
c1 → 中 3
c2 → 差 5

2. 每個詞在句子中出現的次數

得到一個字典數據
evalation [2, 5, 3]
半價 [0, 5, 0]
劃算 [1, 1, 0]
不錯 [0, 2, 0]
·········
不滿 [0, 1, 0]
重要 [0, 1, 0]
清楚 [0, 1, 0]
具體 [0, 1, 0]
每個詞(特征)后的 list坐標位：0，1，2分別對應好，中，差

以上工作完成之后，就是把模型訓練好了，只不過數據越多越準確

測試

比如輸入一個句子

世紀聯華(百聯西郊購物中心店)的點評 一個號稱國際大都市，收銀處的人服務態度差到極點。銀聯活動30-10，還不可以連單。

得到結果

c2-差