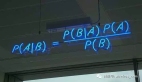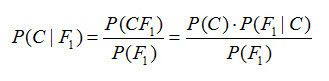在概率論的發展歷史上，先后出現過三種定義：經典定義、頻率定義和主觀定義。

前兩種我們在先前文章中有提到，而主觀主義指的就是今天這篇文章中要講的貝葉斯概率。

貝葉斯概率是以發明人的名字命名的。貝葉斯本人是一名牧師，于1761年去世，但貝葉斯定理的正式提出和公開討論是在1763年，是由貝葉斯的同事代為發表的。

提起貝葉斯概率，在基于統計的機器學習崛起后，它的名字可謂響當當。而且它在概率論三定義中出現又是最晚，有后發優勢。

因此，許多同學可能會覺得貝葉斯概率真是含著金鑰匙出生、一路順風順水的天賜之選啊。

然而，真正了解貝葉斯概率跌宕起伏的經歷之后，可能會發出驚嘆，算法也如人生啊，人生要經歷的磨難算法那里一點也不遜色。

在本篇文章中，我們先簡要一下貝葉斯概率的公式，然后列舉一個典型的通過貝葉斯概率來解決的郵件分類案例。

接下來，我們再來看一下歷史上貝葉斯概率所經歷的從悲劇到喜劇的坎坷歷程，以及探討背后的深層次原因。

最后，我們將探討一下貝葉斯概率在AI中的廣泛應用。

1.貝葉斯概率公式

我們先看一下貝葉斯概率的公式：

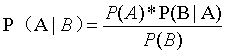
這個公式中包含4項，下面分別說明一下：

先驗概率P(A)

主觀概率，指的是基于人們主觀判斷和信念而得出的關于某個隨機事件發生可能性大小的估計值。

值得一提的是，貝葉斯概率最開始的悲慘命運，其實主要與P（A）體現出來的主觀有關系。

后驗概率P(A|B)

后驗概率是在觀察到某些證據或數據后，對某一事件發生概率的重新評估。

似然函數P(B|A)

似然函數確切來說不是概率，因為是根據已經發生的結果數據來計算。

全（邊緣）概率P(B)

全概率公式提供了一種方法，將一個復雜事件的總概率分解為若干個更簡單事件的概率的加權和。

似乎每一個都很難懂的樣子！先驗概率p(A)反而是看著最容易容易的一個。

后驗概率P(A|B)和似然函數P(B|A)其實都是條件概率，只是在貝葉斯中所處的位置和作用不同，因此在概念上區分開。

條件概率是指一個事件在另一個事件已經發生的條件下發生的概率。以P(A|B)為例，它表示“在B發生的情況下A發生的概率”。

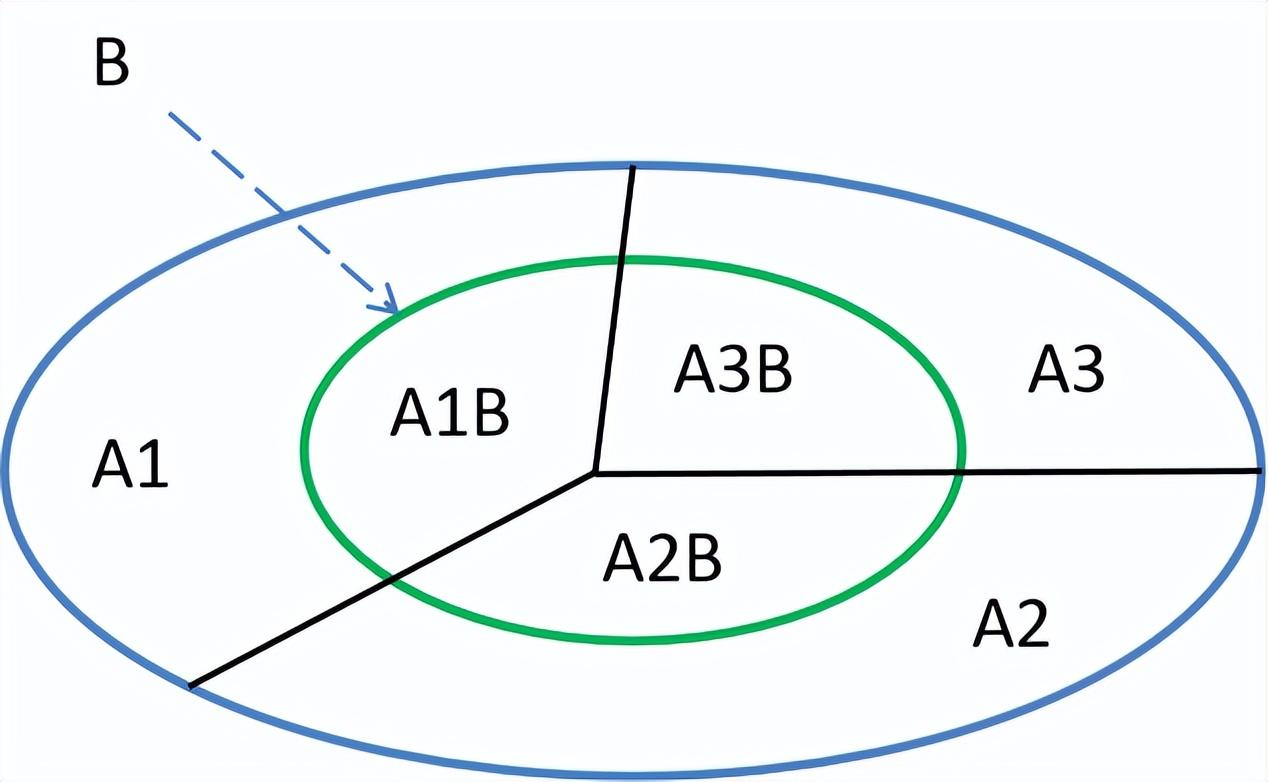
以下面幾何圖形為例，條件概率計算時，將得到的部分再次設定為整體，并排除掉沒有可能性的各個事件之后，重新計算出的比率，如下所示。

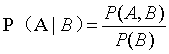
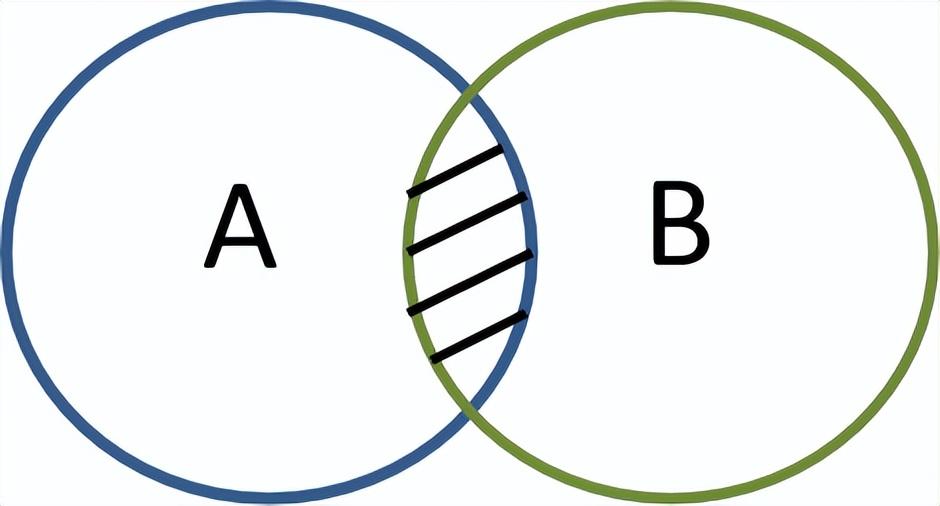
最后，再來看一下全概率或邊緣概率，如下幾何圖形所示。將樣本空間B分解為一系列互不相交的事件，并計算這些事件發生的概率之和等于1，計算公式如下。

P(B) = P(A1)*P(B|A1) + P(A2)*P(B|A2) + P(A3)*P(B|A3)

在現實中，全概率往往是最難求解的一項，因為促使樣本空間分解的因素往往列不全。

2.垃圾郵件過濾的典型案例

看完上面的數學公式部分之后，相信許多同學記不住。這不能怪你們自己，純粹的抽象數學公式就是比較反人性的。

有兩種方式可以幫忙大家更好地理解貝葉斯概率。一是了解貝葉斯概率的背景和真正目的；另一個是通過具體案例。

先來說第一個。貝葉斯當時為什么要提出這種概率出來呢？他想要解決的問題是什么呢？

實際上，貝葉斯的目的很明確，他想要解決的是逆概率問題。

下面是當時他要求解的問題：“想象一張桌子，上面均勻隨機地放著一個白球，而貝葉斯本人背向桌子，對白球位置一無所知。然后，貝葉斯必須從白球位置引出的結果出發，判斷這個位置，或者至少給出對應的可能性”。

當然，貝葉斯這個例子不好理解，后面在拉普拉斯那篇文章中，將給出一個更直觀的例子。

然而，既然我們知道貝葉斯概率是希望求解逆概率問題。那么，我們可以將上面的數學公式替換一下，這樣能幫助大家更好的理解。

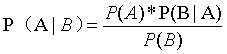
相當于

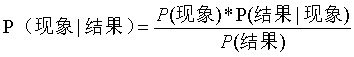
因為，正概率說的是先有現象，然后去推測結果發生的概率。

那么，所謂的逆概率，就是在知道結果的情況下去反推現象（也可以理解成原因）出現的概率。

接下來，我們再通過一個垃圾郵件分類的例子，讓大家直觀地感受一下貝葉斯概率的應用。

構建郵件數據集

構建一個簡化的貝葉斯垃圾郵件過濾數據集。

郵件特征

只考慮兩個特征，即郵件中是否包含“免費”、“中獎”這兩個詞

郵件類別

郵件分為兩類，垃圾郵件（Spam）和非垃圾郵件（Not Spam）

先驗概率

假設我們從歷史數據中得知，垃圾郵件占所有郵件的30%，非垃圾郵件占70%

P(Spam) = 0.3

P(Not Spam) = 0.7

條件概率

假設在垃圾郵件中，包含“免費”的概率是80%，包含“中獎”的概率是70%

P(免費|Spam) = 0.8

P(中獎|Spam) = 0.7

在非垃圾郵件中，包含“免費”的概率是10%，包含“中獎”的概率是5%

P(免費|Not Spam) = 0.1

P(中獎|Not Spam) = 0.05

新郵件特征

假設我們收到一封新郵件，它同時包含“免費”和“中獎”兩個詞

使用貝葉斯定理計算后驗概率

我們需要計算這封郵件是垃圾郵件的概率P(Spam|免費，中獎)和不是垃圾郵件的概率P(Not Spam|免費，中獎)

使用貝葉斯定理，我們可以得到

由于我們假設免費和中獎是獨立的，我們可以得到垃圾郵件中的聯合概率

P(免費，中獎|Spam) = P(免費|Spam)* P(中獎|Spam) = 0.8*0.7 = 0.56

P(免費，中獎|Not Spam) = P(免費|Not Spam)* P(中獎|Not Spam) = 0.1*0.05 = 0.005

決策

因此，該封郵件是垃圾郵件的概率更大一些。

3.貝葉斯概率從悲劇到喜劇的三段經歷

貝葉斯概率從誕生到AI時代的火熱，大致經歷了以下三個階段。

第一階段：從出現到確立

核心事件1：1763年，托馬斯貝葉提出貝葉斯定理，求解逆概率問題；

核心事件2：1774年，拉普拉斯發表《論事件原因存在概率》，綜合了正、逆概率，貝葉斯正式作為逆概率的標準。

第二階段：從寒冬到曙光

核心事件1：拉普拉斯方法中的主觀置信度（即貝葉斯概率部分）受到強烈批評，如哲學家密爾形容為“心智失常”，“自稱是科學，其實是無知”，統計學家費希爾“謬誤的垃圾”；

核心事件2：20世紀初，數理統計學科出現，主流統計學將貝葉斯概率排斥之外；

核心事件3：1933年，安德烈.柯爾莫洛夫，提出概率公理，柯爾莫洛本人是頻率學派。

第三階段：從認可到爆發

核心事件1：20世紀50年代，薩維奇發布《統計學基礎》，提出貝葉斯公式是唯一的推理工具；

核心事件2：20世紀60年代，雷所羅門諾夫將圖靈的可計算性理論與貝葉斯公式結合起來，這就是人工智能一般性框架的前身；

核心事件3：20世紀80年代，蒙特卡洛模擬方法的出現，特別是馬爾科夫鏈蒙特卡洛方法（MAMC），給貝葉斯公式的實際應用帶來了革命。

4.貝葉斯概率坎坷歷程的原因剖析

從上面貝爾斯概率的經歷中，可以發現貝葉斯概率在歷史上大部分時間之內，都處于一種邊緣、受排斥的位置上。

它只是一種數學方法而已，原因到底為何呢？

一是計算復雜性，古代沒有計算機，計算器也沒有.而在貝葉斯定理中，計算后驗概率通常需要對所有可能的參數值進行積分，這在數學計算上是比較復雜的。

在計算技術不發達的時代，這種計算上的困難限制了貝葉斯方法的廣泛應用。但是，顯然這個原因頂多會導致不使用，不至于受排斥。

二是主觀性問題，貝葉斯定理依賴于先驗概率，即在觀察數據之前對事件發生概率的估計。

這種先驗概率的設定被認為帶有主觀性，因為不同的人可能會基于不同的信息或信念設定不同的先驗概率。

在科學界，尤其是頻率學派的統計學家看來，這種主觀性是不可接受的，他們更傾向于基于數據本身來估計概率，而不依賴于任何先驗信息。

在我們看來，主觀或者客觀更多的是的一種認識和利用世界的手段而已，顯然還有更深層次的原因。

三是秩序性問題，這才是貝葉斯定律在歷史上遭遇冷遇的根本原因。在哲學的理性主義時代，人們普遍認為真理是客觀存在的，這種秩序觀強調世界的運行遵循固定的、可預測的規律，而這些規律是獨立于人的主觀意識的。

換句話說，社會中的分層、權威等也是客觀決定的，不決定于人主觀的意識，否則社會只會變得混亂。

接著，我們再來探討一下，歷史上又是那些因素最終拯救了貝葉斯概率呢？

首先，計算機與馬爾科夫鏈蒙特卡洛（MCMC）方法的出現，從根本上解決了貝葉斯方法在算力和積分計算上的瓶頸。

當然，這不是主要原因，因為如果人們的認知不發生改變的話，再好的工具放在手里都起不到應有的作用。

其次，實用主義哲學的興起，為貝葉斯概率理論提供了堅實的哲學基礎，解決了主觀與客觀之間的長期爭論。

實用主義強調“好不好用”，而不刻意追求所謂的“正不正確”。在這一哲學背景下，貝葉斯方法中先驗概率的主觀性不再是障礙。

這一觀念的轉變，最終使得貝葉斯概率理論從邊緣走向主流，被廣泛接受為處理不確定性問題的有效工具。

5.貝葉斯概率在AI中的應用

貝葉斯概率理論作為統計學與人工智能領域的一顆璀璨明珠，其影響力深遠，構成了貝葉斯學習、貝葉斯推理、貝葉斯網絡、貝葉斯決策以及貝葉斯優化等一系列核心理論的基石。

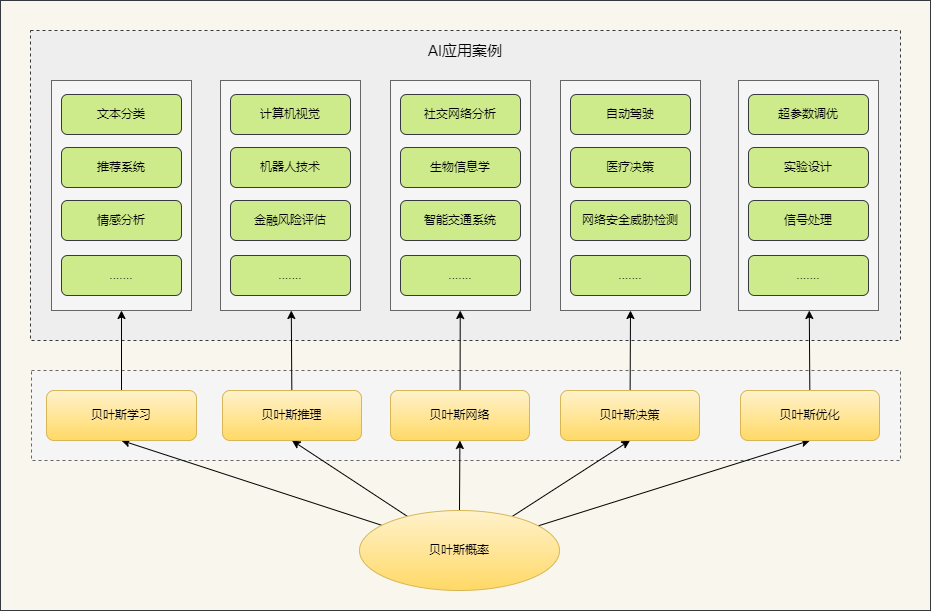
一是貝葉斯學習。它的優勢在于其獨特的增量學習能力，它允許模型在訓練過程中不斷更新參數的概率分布。

這種動態調整的能力使得模型能夠適應不斷變化的數據環境，實現自我優化和提升，特別適合在處理變化數據和在線學習場景中。

二是貝葉斯推理。它作為一種基于貝葉斯定理的統計推理方法，不僅能夠提供參數的點估計，更重要的是，它能夠提供參數的分布信息，這為理解和量化模型的不確定性提供了有力工具。

在AI領域，貝葉斯推理被廣泛應用于不確定性量化、模型選擇和模型比較，為決策提供更全面、更可靠的依據。

三是貝葉斯網絡。作為一種概率圖模型，通過有向無環圖（DAG）巧妙地表示變量之間的條件依賴關系，為處理復雜不確定性問題提供了強大的工具。

在知識表示、推理、預測和決策支持系統中，貝葉斯網絡的應用無處不在，它能夠幫助我們理解和預測復雜系統的動態行為，為決策提供科學依據。

四是貝葉斯決策。它將貝葉斯概率與決策理論完美結合，為在不確定性下做出最優決策提供了系統性的解決方案。

它考慮了決策的后果和不確定性，通過最小化預期損失或最大化預期效用，可以幫助我們在復雜多變的環境中做出更適合的選擇。

五是貝葉斯優化。通過構建目標函數的概率模型，貝葉斯優化能夠高效地搜索最優解，尤其適用于高維、非凸或計算成本高的優化問題，如超參數調優、神經架構搜索和實驗設計等。

6.小結

人生就像是一個大戲臺，不同的人在舞臺上扮演著不同的角色。同樣，算法的世界也是一方廣闊的舞臺，不同的算法的命運也各不相同。

像貝葉斯算法，盡管生不逢時，但正如金子早晚會發光，貝葉斯算法也在人類文明逐步走向數字化、智能化的路途中，發展成為一個舉足輕重的算法。

并且，貝葉斯概率，如今也已經超越了其最初的數學領域，成為了一種理解和解釋世界的哲學。