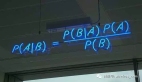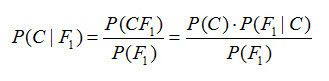貝葉斯機器學習:經典模型與代碼實現!
貝葉斯定理是概率模型中最著名的理論之一,在機器學習中也有著廣泛的應用。基于貝葉斯理論常用的機器學習概率模型包括樸素貝葉斯和貝葉斯網絡。本文在對貝葉斯理論進行簡介的基礎上,分別對樸素貝葉斯和貝葉斯網絡理論進行詳細的推導并給出相應的代碼實現,針對樸素貝葉斯模型,本文給出其NumPy和sklearn的實現方法,而貝葉斯網絡的實現則是借助于pgmpy。
貝葉斯理論簡介
自從Thomas Bayes于1763年發表了那篇著名的《論有關機遇問題的求解》一文后,以貝葉斯公式為核心的貝葉斯理論自此發展起來。貝葉斯理論認為任意未知量都可以看作為一個隨機變量,對該未知量的描述可以用一個概率分布來概括,這是貝葉斯學派最基本的觀點。當這個概率分布在進行現場試驗或者抽樣前就已確定,便可將該分布稱之為先驗分布,再結合由給定數據集 X 計算樣本的似然函數后,即可應用貝葉斯公式計算該未知量的后驗概率分布。經典的貝葉斯公式表達如下:
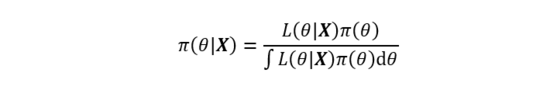
上式左邊為后驗分布,右邊分母為邊緣分布,其排除了任何有關未知量的信息,因此貝葉斯公式的等價形式可以寫作為:
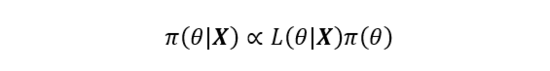
上式可以歸納出貝葉斯公式的本質就是基于先驗分布和似然函數的統計推斷。其中先驗分布的選擇與后驗分布的推斷是貝葉斯領域的兩個核心問題。先驗分布的選擇目前并沒有統一的標準,不同的先驗分布對后驗計算的準確度有很大的影響,這也是貝葉斯領域的研究熱門之一;后驗分布曾因復雜的數學形式和高維數值積分使得后驗推斷十分困難,而后隨著計算機技術的發展,基于計算機軟件的數值技術使得這些問題得以解決,貝葉斯理論又重新煥發活力。
與機器學習的結合正是貝葉斯理論的主要應用方向。樸素貝葉斯理論是一種基于貝葉斯理論的概率分類模型,而貝葉斯網絡是一種將貝葉斯理論應用到概率圖中的分類模型。
樸素貝葉斯
樸素貝葉斯原理與推導
樸素貝葉斯是基于貝葉斯定理和特征條件獨立假設的分類算法。具體而言,對于給定的訓練數據,樸素貝葉斯先基于特征條件獨立假設學習輸入和輸出的聯合概率分布,然后對于新的實例,利用貝葉斯定理計算出最大的后驗概率。樸素貝葉斯不會直接學習輸入輸出的聯合概率分布,而是通過學習類的先驗概率和類條件概率來完成。樸素貝葉斯的概率計算公式如圖1所示。
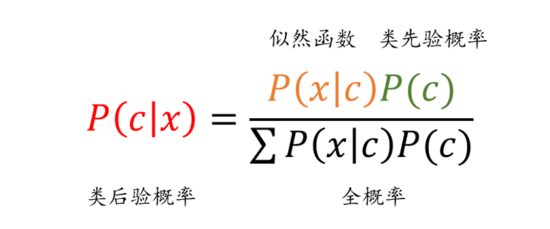
圖1 樸素貝葉斯基本公式
樸素貝葉斯中樸素的含義,即特征條件獨立假設,條件獨立假設就是說用于分類的特征在類確定的條件下都是條件獨立的,這一假設使得樸素貝葉斯的學習成為可能。假設輸入特征向量為X,輸出為類標記隨便變量Y,P(X,Y)為X和Y的聯合概率分布,T為給定訓練數據集。樸素貝葉斯基于訓練數據集來學習聯合概率分布 P(X,Y ) 。具體地,通過學習類先驗概率分布和類條件概率分布來實現。
樸素貝葉斯學習步驟如下。先計算類先驗概率分布:
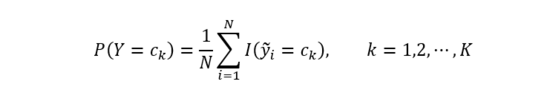
其中Ck表示第k個類別,yi表示第i個樣本的類標記。類先驗概率分布可以通過極大似然估計得到。
然后計算類條件概率分布:
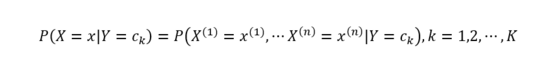
直接 對P(X=x|Y=Ck) 進行估計不太可行,因為參數量太大。 但是樸素貝葉斯的一個最重要的假設就是條件獨立性假設,即:
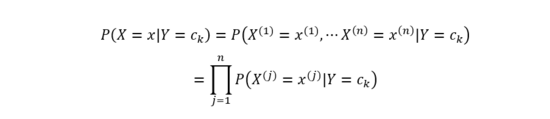
有了條件獨立性假設之后,便可基于極大似然估計計算類條件概率。
類先驗概率分布和類條件概率分布都計算得到之后,基于貝葉斯公式即可計算類后驗概率:
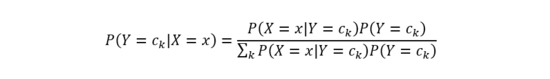
代入類條件計算公式,有:
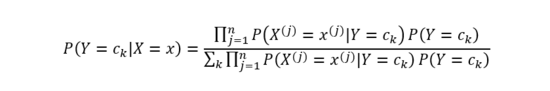
基于上式即可學習一個樸素貝葉斯分類模型。給定新的數據樣本時,計算其最大后驗概率即可:
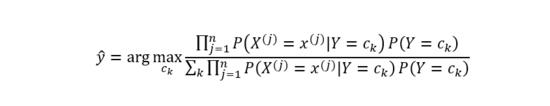
其中,分母 對于所有的 都是一樣的,所以上式 可進一步簡化為:
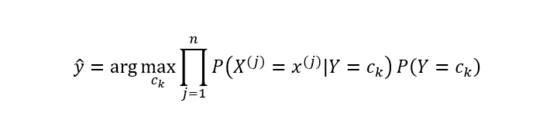
以上就是樸素貝葉斯分類模型的簡單推導過程。
基于NumPy的樸素貝葉斯實現
本節我們基于NumPy來實現一個簡單樸素貝葉斯分類器。樸素貝葉斯因為條件獨立性假設變得簡化,所以實現思路也較為簡單,這里我們就不給出實現的思維導圖了。根據前述推導,關鍵在于使用極大似然估計方法計算類先驗概率分布和類條件概率分布。
我們直接定義樸素貝葉斯模型訓練過程,如代碼1所示。
- def nb_fit(X, y):
- classes = y[y.columns[0]].unique()
- class_count = y[y.columns[0]].value_counts()
- class_prior = class_count/len(y)
- prior = dict()
- for col in X.columns:
- for j in classes:
- p_x_y = X[(y==j).values][col].value_counts()
- for i in p_x_y.index:
- prior[(col, i, j)] = p_x_y[i]/class_count[j]
- return classes, class_prior, prior
在代碼1中,給定數據輸入和輸出均為Pandas數據框格式,先對標簽類別數量進行統計,并以此基于極大似然估計計算類先驗分布。然后對數據特征和類別進行循環遍歷,計算類條件概率。
式(10)作為樸素貝葉斯的核心公式,接下來我們需要基于式(10)和nb_fit函數返回的類先驗概率和類條件概率來編寫樸素貝葉斯的預測函數。樸素貝葉斯的預測函數如代碼2所示。
- def predict(X_test):
- res = []
- for c in classes:
- p_y = class_prior[c]
- p_x_y = 1
- for i in X_test.items():
- p_x_y *= prior[tuple(list(i)+[c])]
- res.append(p_y*p_x_y)
- return classes[np.argmax(res)]
代碼2中定義了樸素貝葉斯的預測函數。以測試樣本X_test作為輸入,初始化結果列表并獲取當前類的先驗概率,對測試樣本字典進行遍歷,先計算類條件概率的連乘,然后計算先驗概率與類條件概率的乘積。最后按照式(21.10)取argmax獲得最大后驗概率所屬的類別。
最后,我們使用數據樣例對編寫的樸素貝葉斯代碼進行測試。手動創建一個二分類的示例數據 ,并對其使用nb_fit進行訓練,如代碼3所示。
- ### 創建數據集并訓練
- # 特征X1
- x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3]
- # 特征X2
- x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L']
- # 標簽列表
- y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1]
- # 形成一個pandas數據框
- df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})
- # 獲取訓練輸入和輸出
- X, y = df[['x1', 'x2']], df[['y']]
- # 樸素貝葉斯模型訓練
- classes, class_prior, prior_condition_prob = nb_fit(X, y)
- print(classes, class_prior, prior_condition_prob)
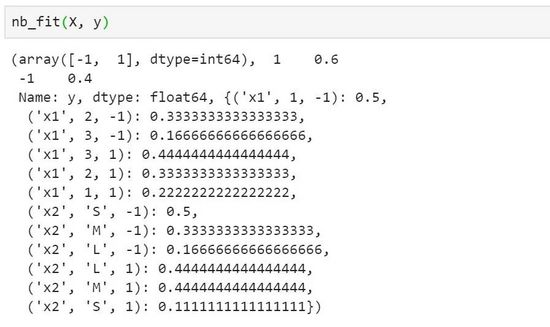
圖2 代碼21-3輸出截圖
在代碼3中,我們基于列表構建了Pandas數據框格式的數據集,獲取訓練輸入和輸出并傳入樸素貝葉斯訓練函數中,輸出結果如圖21.2所示。可以看到,數據標簽包括是1/-1的二分類數據集,類先驗概率分布為{1:0.6,-1:0.4},各類條件概率如圖中所示。
最后,我們創建一個測試樣本,并基于nb_predict函數對其進行類別預測,如下所示。
- ### 樸素貝葉斯模型預測
- X_test = {'x1': 2, 'x2': 'S'}
- print('測試數據預測類別為:', nb_predict(X_test))
輸出:
- 測試數據預測類別為:-1
最后模型將該測試樣本預測為負類。
基于sklearn的樸素貝葉斯實現
sklearn也提供了樸素貝葉斯的算法實現方式,sklearn為我們提供了不同似然函數分布的樸素貝葉斯算法實現方式。比如高斯樸素貝葉斯、伯努利樸素貝葉斯、多項式樸素貝葉斯等。我們以高斯樸素貝葉斯為例,高斯樸素貝葉斯即假設似然函數為正態分布的樸素貝葉斯模型。高斯樸素貝葉斯的似然函數如下式所示。
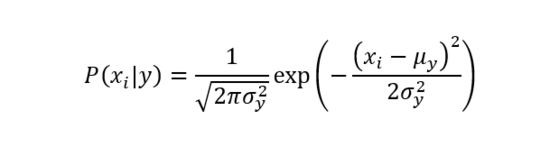
sklearn中高斯樸素貝葉斯的調用接口為sklearn.naive_bayes.GaussianNB,以iris數據集為例給出調用示例,如代碼4所示。
- ### sklearn高斯樸素貝葉斯示例
- # 導入相關庫
- from sklearn.datasets import load_iris
- from sklearn.model_selection import train_test_split
- from sklearn.naive_bayes import GaussianNB
- from sklearn.metrics import accuracy_score
- # 導入數據集
- X, y = load_iris(return_X_y=True)
- # 數據集劃分
- X_train, X_test, y_train, y_test =
- train_test_split(X, y, test_size=0.5, random_state=0)
- # 創建高斯樸素貝葉斯實例
- gnb = GaussianNB()
- # 模型擬合并預測
- y_pred = gnb.fit(X_train, y_train).predict(X_test)
- print("Accuracy of GaussianNB in iris data test:", accuracy_score(y_test, y_pred))
輸出:
- Accuracy of GaussianNB in iris data test:0.9466666666666667
在代碼4中,先導入sklearn中樸素貝葉斯相關模塊,導入iris數據集并進行訓練測試劃分。 然后創建高斯樸素貝葉斯模型實例,基于訓練集進行擬合并對測試集進行預測,最后準確率為0.947。
貝葉斯網絡
貝葉斯網絡原理與推導
樸素貝葉斯的最大的特點就是特征的條件獨立假設,但在現實情況下,條件獨立這個假設通常過于嚴格,在實際中很難成立。特征之間的相關性限制了樸素貝葉斯的性能,所以本節我們將繼續介紹一種放寬了條件獨立假設的貝葉斯算法,即貝葉斯網絡(bayesian network)。
我們先以一個例子進行引入。假設我們需要通過頭像真實性、粉絲數量和動態更新頻率來判斷一個微博賬號是否為真實賬號。各特征屬性之間的關系如圖3所示。
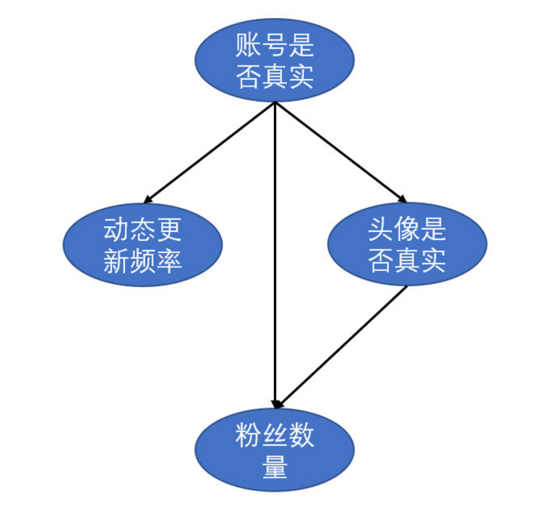
圖3 微博賬號屬性關系
圖3是一個有向無環圖(directed acyclic graph,DAG),每個節點表示一個特征或者隨機變量,特征之間的關系則是用箭頭連線來表示,比如說動態的更新頻率、粉絲數量和頭像真實性都會對一個微博賬號的真實性有影響,而頭像真實性又對粉絲數量有一定影響。但僅有各特征之間的關系還不足以進行貝葉斯分析。除此之外,貝葉斯網絡中每個節點還有一個與之對應的概率表。假設賬號是否真實和頭像是否真實有如下概率表:
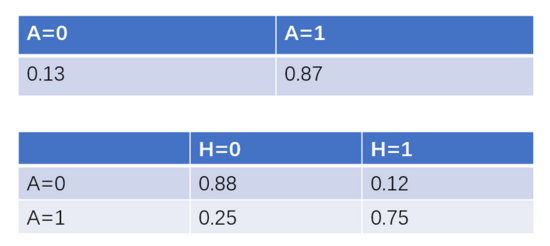
圖4 貝葉斯網絡概率表
圖4是體現頭像和賬號是否真實的概率表。第一張概率表表示的是賬號是否真實,因為該節點沒有父節點,可以直接用先驗概率來表示,表示賬號真實與否的概率。第二張概率表表示的是賬號真實性對于頭像真實性的條件概率。比如說在頭像為真實頭像的條件下,賬號為真的概率為0.88。在有了DAG和概率表之后,我們便可以利用貝葉斯公式進行定量的因果關系推斷。假設我們已知某微博賬號使用了虛假頭像,那么其賬號為虛假賬號的概率可以推斷為:
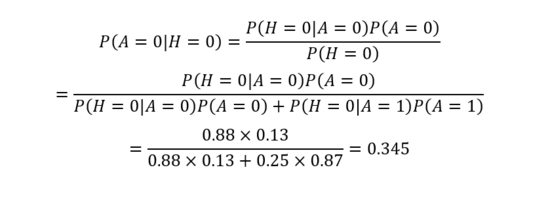
利用貝葉斯公式,我們可知在虛假頭像的情況下其賬號為虛假賬號的概率為0.345。
通過上面的例子我們直觀的感受到貝葉斯網絡的用法。一個貝葉斯網絡通常由有向無環圖和節點對應的概率表組成。其中DAG由節點(node)和有向邊(edge)組成,節點表示特征屬性或隨機變量,有向邊表示各變量之間的依賴關系。貝葉斯網絡的一個重要性質是:當一個節點的父節點概率分布確定之后,該節點條件獨立于其所有的非直接父節點。這個性質方便于我們計算變量之間的聯合概率分布。
一般來說,多變量非獨立隨機變量的聯合概率分布計算公式如下:
有了節點條件獨立性質之后,上式可以簡化為:
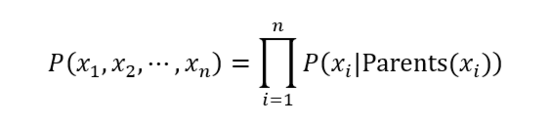
當由DAG表示節點關系和概率表確定后,相關的先驗概率分布、條件概率分布就能夠確定,然后基于貝葉斯公式,我們就可以使用貝葉斯網絡進行推斷。
借助于pgmpy的貝葉斯網絡實現
本小節基于pgmpy來構造貝葉斯網絡和進行建模訓練。pgmpy是一款基于Python的概率圖模型包,主要包括貝葉斯網絡和馬爾可夫蒙特卡洛等常見概率圖模型的實現以及推斷方法。
我們以學生獲得的推薦信質量的例子來進行貝葉斯網絡的構造。相關特征之間的DAG和概率表如圖5所示。
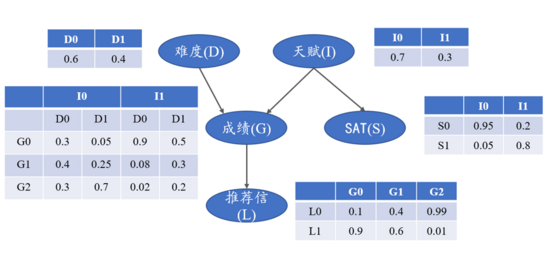
圖5 推薦信質量的DAG和概率表
由圖5可知,考試難度、個人聰明與否都會影響到個人成績,另外個人天賦高低也會影響到SAT分數,而個人成績好壞會直接影響到推薦信的質量。下面我們直接來用pgmpy實現上述貝葉斯網絡模型。
(1)構建模型框架,指定各變量之間的關系。如代碼5所示。
- # 導入pgmpy相關模塊
- from pgmpy.factors.discrete import TabularCPD
- from pgmpy.models import BayesianModel
- letter_model = BayesianModel([('D', 'G'),
- ('I', 'G'),
- ('G', 'L'),
- ('I', 'S')])
(2)構建各個節點的條件概率分布,需要指定相關參數和傳入概率表,如代碼6所示。
- # 學生成績的條件概率分布
- grade_cpd = TabularCPD(
- variable='G', # 節點名稱
- variable_card=3, # 節點取值個數
- values=[[0.3, 0.05, 0.9, 0.5], # 該節點的概率表
- [0.4, 0.25, 0.08, 0.3],
- [0.3, 0.7, 0.02, 0.2]],
- evidence=['I', 'D'], # 該節點的依賴節點
- evidence_card=[2, 2] # 依賴節點的取值個數
- )
- # 考試難度的條件概率分布
- difficulty_cpd = TabularCPD(
- variable='D',
- variable_card=2,
- values=[[0.6], [0.4]]
- )
- # 個人天賦的條件概率分布
- intel_cpd = TabularCPD(
- variable='I',
- variable_card=2,
- values=[[0.7], [0.3]]
- )
- # 推薦信質量的條件概率分布
- letter_cpd = TabularCPD(
- variable='L',
- variable_card=2,
- values=[[0.1, 0.4, 0.99],
- [0.9, 0.6, 0.01]],
- evidence=['G'],
- evidence_card=[3]
- )
- # SAT考試分數的條件概率分布
- sat_cpd = TabularCPD(
- variable='S',
- variable_card=2,
- values=[[0.95, 0.2],
- [0.05, 0.8]],
- evidence=['I'],
- evidence_card=[2]
- )
(3)將各個節點添加到模型中,構建貝葉斯網絡。如代碼7所示。
- # 將各節點添加到模型中,構建貝葉斯網絡
- letter_model.add_cpds(
- grade_cpd,
- difficulty_cpd,
- intel_cpd,
- letter_cpd,
- sat_cpd
- )
- # 導入pgmpy貝葉斯推斷模塊
- from pgmpy.inference import VariableElimination
- # 貝葉斯網絡推斷
- letter_infer = VariableElimination(letter_model)
- # 天賦較好且考試不難的情況下推斷該學生獲得推薦信質量的好壞
- prob_G = letter_infer.query(
- variables=['G'],
- evidence={'I': 1, 'D': 0})
- print(prob_G)
輸出如圖6所示。
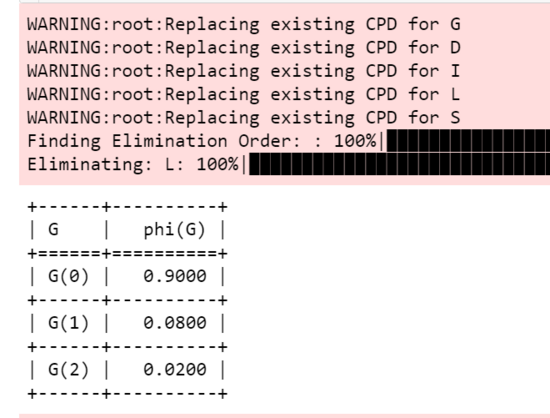
從圖6的輸出結果可以看到,當聰明的學生碰上較簡單的考試時,獲得第一等成績的概率高達90%。
小結
貝葉斯定理是經典的概率模型之一,基于先驗信息和數據觀測得到目標變量的后驗分布的方式,是貝葉斯的核心理論。貝葉斯理論在機器學習領域也有廣泛的應用,最常用的貝葉斯機器學習模型包括樸素貝葉斯模型和貝葉斯網絡模型。
樸素貝葉斯模型是一種生成學習方法,通過數據學習聯合概率分布的方式來計算后驗概率分布。之所以取名為樸素貝葉斯,是因為特征的條件獨立性假設,能夠大大簡化樸素貝葉斯算法的學習和預測過程,但也會帶來一定的精度損失。
進一步地,將樸素貝葉斯的條件獨立假設放寬,認為特征之間是存在相關性的貝葉斯模型就是貝葉斯網絡模型。貝葉斯網絡是一種概率無向圖模型,通過有向圖和概率表的方式來構建貝葉斯概率模型。當由有向圖表示節點關系和概率表確定后,相關的先驗概率分布、條件概率分布就能夠確定,然后基于貝葉斯公式,就可以使用貝葉斯網絡進行概率推斷。
本文參考代碼地址:
https://github.com/luwill/Machine_Learning_Code_Implementation/tree/master/charpter21_Bayesian_models