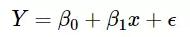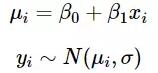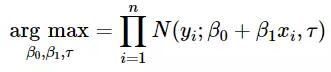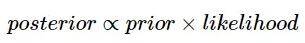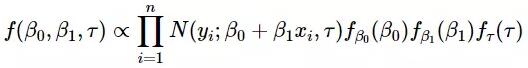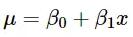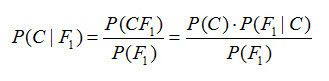不想去健身房的我,最后被貝葉斯分析說服了...
大數據文摘出品
編譯:Zhifu、JonyKai、湯圓、夏雅薇
可能經常你會聽到一些很主觀的評價比如“你太瘦了”或者“你怎么那么高”,但這里瘦或者高都是基于評價者的主觀判斷和視覺記憶做出的評述,并沒有嚴格的參照。
作者從小被人說體型瘦小,于是他用了貝葉斯分析最終得出了自己的體重確實低于本國平均水平的結論。沒有比直白的數字更有說服力了,想要說服自己健身的小伙伴不妨也試試作者的統計學暴擊法!
這篇文章將敘述一個在線性回歸理論中應用貝葉斯分析的有趣試驗(一個小秘密:我在這篇文章中使用了公制計量單位呦)。
如文章標題所述,我將會對自己的體格進行一番科學的研究。
在開始之前,我希望大家多了解我一些:我在越南出生,在新加坡上高中,現在在美國上大學。我經常因為身形瘦小被人們取笑,說我應該多去健身房鍛煉增肌,擁有更強壯的體魄。這些評價我一般都一笑置之。對于一個身高169厘米(5尺6寸),體重58公斤(127磅)的人來說,我的BMI指數(20.3)幾近***。
仔細一想,大家可能沒說錯:我比一般的越南男性要高,但卻只有平均體重(維基百科里越南男性的平均體重是58公斤,平均身高是162厘米),“看起來”可能是要稍微瘦一些。
這里“看起來”是關鍵:背后的邏輯很清楚,不是嗎?如果你把自己抻長一些,體重不變,那確實應該看起來苗條一些。我把這個看作是嚴肅的科學問題,并準備深入研究。
對于一個169厘米高的越南男性來說,我到底輕了多少呢?
我們需要一種有理有據的方式來研究這個問題。有個好方法是盡可能多地找到越南男子身高和體重的數據,來判斷我在這個樣本中的位置。
越南人口數據
在瀏覽各種網頁后,我找到了一份調查研究數據,包含超過10,000名越南人的人口統計信息。將抽樣條件設置為年齡18-29歲的越南男性,從而得到數量為383的樣本,這個樣本足以用來進行接下來的分析啦。
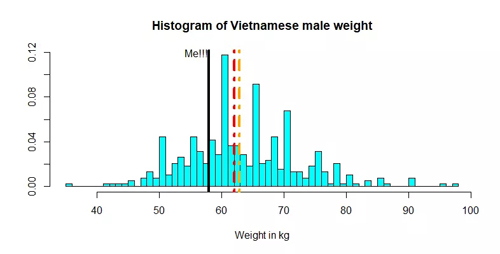
首先,通過人口體重的直方圖,看看我在年輕越南男性中的體重分布位置。
紅線表示樣本的中位數,而橙色線表示平均值
這張直方圖表明我的體重略低于383名年輕越南男子的體重平均值和中位數。看起來是與我們要研究的相關呀!然而問題并不在于我的體重與這個樣本本身的比較,是假設這383個人可以代表越南男性,在身高169厘米的情況下,我的體重與整個越南人口相比處于一個什么位置。為此,我們需要進行回歸分析。
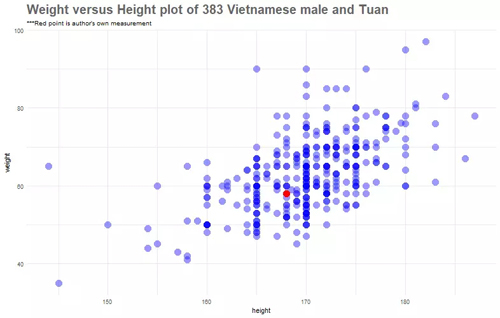
首先繪制一個身高和體重的二維散點圖
好吧,看起來我處在平均水平。但是如果我們只看身高169厘米的數據(想象一條垂直x軸于169厘米這個刻度并穿過紅點的直線),我的體重在他們之中處于下游。
另一個重要的發現是越南男性身高和體重呈正相關。我們將進行定量分析來進一步了解這種關系。
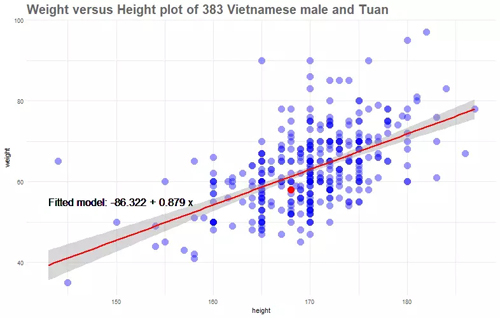
首先,讓我們快速添加“普通最小二乘”線。我稍后會詳細介紹這一點,現在先在圖上展示出來。
最小二乘線可以表示為y = -86.32 + 0.889x,這表明通常情況下,我這個年齡的越南男性,每增加1厘米的身高,體重會增加0.88千克。
但是,這并沒有解決我們的問題;身高169厘米,體重58公斤到底是太沉,太輕還是剛剛好呢?要以定量的方式進一步解釋這個問題,如果有所有身高1米68的人的體重分布,那么我的體重排在前25%,50%或75%的幾率是多少?要弄清這一點,我們需要深入學習并理解回歸背后的理論。
線性回歸理論
在線性回歸模型中,Y變量(在我們的例子中,是人的體重)是x(身高)的線性函數。在這個線性關系中截距和斜率分別為β0和β1;也就是說,假設E(Y | X = x)=β0+β1x。我們不知道β0和β1是多少,所以將它們視為未知參數。
在大多數標準線性回歸模型中,我們進一步假設給定X = x的情況下,Y的條件分布是正態分布的。
這就是基本的線性回歸模型:
可以被改寫成:
注意,在許多模型中,我們可以用精度參數τ替換方差參數σ,其中τ= 1 /σ。
總結:因變量Y遵循由平均數μi和精度參數τ決定的正態分布。μi是由β0和β1決定的X的線性函數。
***,我們還需假設未知方差不依賴于x;這種假設稱為同方差性。
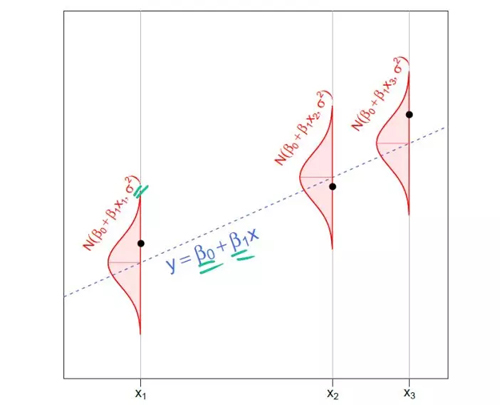
涉及的內容很多,都涵括在下面這張圖里啦。
圖像來源:Joseph Chang(耶魯大學)
在實際的數據分析問題中,我們掌握的只是黑點 - 數據。使用這些數據,我們的目標是推斷不知道的事情,包括β0,β1(在圖片中的藍色虛線)和σ(它決定了在給定一個y值的時候,紅色正態分布密度的寬度)。注意,每個黑點周圍的正態分布看起來完全相同。這是同方差性的本質。
估算參數
現在,有幾種方法可以估算β0和β1。如果你使用普通最小二乘估計這樣的模型,你不必擔心概率公式,因為你正在尋找β0和β1的***值,而這是通過最小化擬合值與預測值的平方誤差得到的。
另一方面,你可以使用***似然估計(MLE)來估計此類模型:通過***化似然函數來尋找參數的***值。
注意:一個有趣的結果(我沒有放上具體的數學證明)是,如果我們假設誤差項也屬于正態分布的話,那么最小二乘估計的結果也是***似然估計的結果。
貝葉斯方法的線性回歸
不同于***化似然函數,貝葉斯方法會假設參數服從一個先驗分布。根據貝葉斯公式計算出參數后驗概率:
貝葉斯方法的似然函數同上面的類似,不同之處在于加入了對估計參數β0,β1,τ的先驗分布:
等等,什么是先驗分布,為什么這會讓公式看上去更加復雜?
請相信我,先驗分布雖然看上去很奇怪,但實際上很直觀。事實上,我們對未知的參數(例子中的β0,β1,τ)分配一個看上去很隨意的先驗分布,這里存在著很強的哲學緣由。
先驗分布能夠反映出在沒看見數據之前我們對數據的假設理解。在觀察過一些數據之后,我們應用貝葉斯公式,就得到了同時考慮到了先驗和數據的未知參數后驗分布。根據后驗分布,我們就能預測出未來的數據的分布。
最終的參數估計雖然取決于數據和先驗分布,但是如果數據中包含的信息越多,那先驗的影響就越小。
那么我該如何選擇先驗分布
這是個好問題,因為這里存在著無數種可能。理論上只有存在一個正確的先驗能夠能夠反應出你的先驗假設。但是在實際中,先驗分布的選取是相當的主觀,甚至有時可以是任意的。
我們可以選擇一個有著較大標準方差(意味著精度很低)的正態分布先驗。比如,我們假設參數β0和β1是服從均值為0標準方差為10000的正態分布。這種分布是毫無信息的分布,因為分布十分平坦(這意味著,參數在任意區間的取值概率幾乎相同)。
如果選取了這種類型的先驗分布,那么我們就不用考慮在這類分布中哪種分布更好,因為分布幾乎都很平坦,在每個地方的概率都可以忽略不計。此外,后驗分布不會受這種分布的影響。
同樣,對于精度τ,因為其必須是非負的,所以需要選取一個取值限定在非負范圍的分布。比如,在這里可以選取一個帶有較小形狀和尺度參數的伽馬分布。
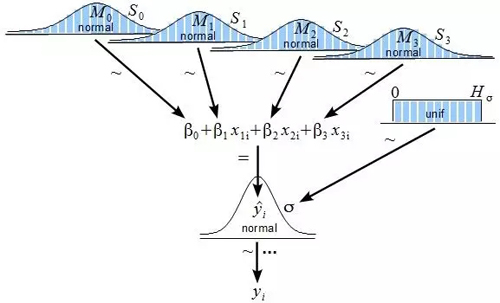
另外一種很有用的不附帶信息的分布是均勻分布。如果對 σ 或 τ選擇了均勻分布,那么你最終將會得到這樣的模型。如下圖所示,由John K. Kruschke繪制。
John K. Kruschke繪制的模型
用R語言和JAGS模擬數據
到目前為止,我們仍只停留在理論階段。大多數情況下。后驗分布并不能直接得到(想想正態分布和伽馬分布有多復雜,然后還要再將他們乘起來)。Markov Chain Monte Carlo方法常常用來估計模型的參數。利用JAGS就能幫我們完成。
“等一下!!!這個工具真能夠幫我們解決這些復雜的公式么?”
JAGS模型是一個基于Markov Chain Monte Carlo(MCMC)的仿真過程,它能夠生成出參數空間θ=(β0;β1;τ)的許多次迭代。由參數空間中每個參數生成的樣本分布會估計出參數最有可能的分布
為什們是這樣呢?這個解釋起來十分復雜,已經超出了本篇介紹的范圍。直接來說就是:MCMC通過構建一個馬爾可夫鏈產生了服從后驗分布的樣本,這個馬爾可夫鏈有著同樣的目標后驗分布!?
這個過程很沒意思。最快的方法就是:不去解等式(2),因為通常不可能得到解析解。我們能做的就是聰明的采樣,而在數學上證明了這些樣本確實服從以β0,β1,τ為參數的分布。
那么揮別了數學之后,我該怎么使用JAGS?
我們按下面的步驟在R語言中運行JAGS
首先以文本的形式寫下模型
然后,我們讓JAGS執行仿真模擬。這里我使用JAGs對參數空間θ進行10000次模擬
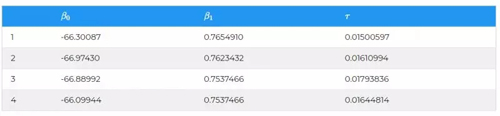
抽樣之后,我們就得到了θ=(β0;β1;τ)的抽樣數據,如下表所示:
“看上去好酷,那又怎樣呢?”
現在我們對參數空間θ進行10000次迭代,根據等式
這就意味著,如果用x=169cm替代每個迭代值,我們將會得到10000個體重值,也就是身高169cm情況下體重的分布。
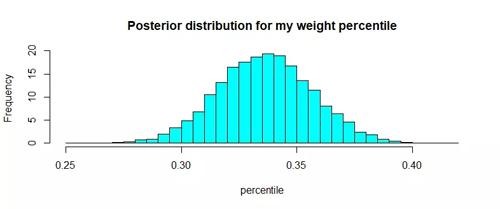
我們都對以我身高為條件下體重的百分比分布很感興趣。為了達到這個目的,需要找到基于我身高的體重分布。
上面這張圖表明我的體重(給定169的身高)最有可能在模擬越南人口中的后30%左右。
比如,我們能發現我的體重在前40%甚至更少的位置
因此大量證據表明,在身高169的條件下,體重58kg會讓我處于越南人口的較低百分比處。我確實需要去健身房鍛煉并增加些體重了。畢竟如果你不信詳盡的貝葉斯統計分析,還能相信什么呢?
我有一份包含了美國8169名年輕男性和女性身高體重的數據(國家壽命調查1997),你能做同樣的分析么,看看你會得到什么樣的結論?
相關報道:
https://towardsdatascience.com/how-bayesian-statistics-convinced-me-to-hit-the-gym-fa737b0a7ac
【本文是51CTO專欄機構大數據文摘的原創譯文,微信公眾號“大數據文摘( id: BigDataDigest)”】