ML之梯度下降算法 機器學習初學者的梯度下降算法
基本概念
本節嘗試獨立于機器學習算法, 單純地來講梯度下降算法 [Gradient Descent, GD], 以使梯度下降更具一般性。
開始之前, 先放 2 個基本概念, 帶著這 2 個認識, 在幾乎不具備機器學習知識的前提下, 應該也能很好地讀懂本節內容:
- 機器學習的主要任務之一, 就是通過訓練, 習得一組最優的參數. 常以成本函數 [Cost Function] 作為參數估計的函數, 因此, 機器學習的任務就轉變為了最小化成本函數.
- 優化是機器學習算法非常重要的組成部分, 幾乎每個機器學習算法都有一個優化算法.
梯度下降算法就是一個被廣泛使用的優化算法, 它可以用于尋找最小化成本函數的參數值. 用中學數學的語言來描述梯度下降, 是這樣的: 當函數 _ 取得最小值時, 求所對應的自變量 的過程_ 此處, 就是機器要學習的參數, 就是用于參數估計的成本函數, 是關于 的函數. 因此, 基本上具備中學數學知識的, 都能理解梯度下降算法.
梯度下降的基本步驟是:
- 對成本函數進行微分, 得到其在給定點的梯度. 梯度的正負指示了成本函數值的上升或下降:
- 選擇使成本函數值減小的方向, 即梯度負方向, 乘以以學習率 計算得參數的更新量, 并更新參數:
- 重復以上步驟, 直到取得最小的成本
以上就是梯度下降算法最基礎也是最核心的概念, 很簡單吧.
下面講講梯度下降算法的幾個變種, 包括: 批量梯度下降 [Batch Gradient Descent, BGD], 隨機梯度下降 [Stochastic Gradient Descent, SGD], 小批量梯度下降 [Mini-Batch Gradient Descent, MBGD]
算法簡介
BGD
BGD 是梯度下降算法最原始的形式, 其特點是每次更新參數 時, 都使用整個訓練集的數據.
BGD 的具體實現是這樣的:
- 設假設函數為:
- 所謂假設函數, 就是用于將輸入映射為輸出的工具, 其返回值也稱為估計值
- 設成本函數為:
- 注意, 才是函數自變量, 是模型輸入, 是輸入對應的真實值
- 該成本函數中, 真正有效的部分是 , 前面的 是為后續計算方便添加的
- 對成本函數求導, 需要對每一個參數 分別求偏導, 得到它們各自的梯度:
- 機器學習模型通常不止一個參數. 成本函數作為參數估計的工具, 要估計每個參數的最優值, 因此需要對每一個參數分別求偏導數
- 每個參數都按梯度負方向進行更新:
因此, BGD 的偽代碼形式可以簡單地寫成:
- repeat {
- (for every j = 0, 1, .. n)
- }
上式中的求和部分 就體現了每一次迭代, 都以整個訓練集為對象進行梯度計算.
BGD 得到的是全局最優解, 因為它總是以整個訓練集來計算梯度, 這是 BGD 的優點. 但也因此帶來了巨大的計算量, 計算迭代速度很很慢.
SGD
SGD 每次以一個樣本, 而不是整個數據集來計算梯度. 因此, SGD 從成本函數開始, 就不必再求和了, 針對單個樣例的成本函數可以寫成: (此處的 同樣是為了后續計算方便設置的)
于是, SGD 的參數更新規則就可以寫成:
SGD 的偽代碼形式如下:
- repeat {
- for i = 1, .., m {
- (for every j = 0, 1, .. n)
- }
- }
SGD 的關鍵點在于以隨機順序選取樣本. 因為 SGD 存在局部最優困境, 若每次都以相同的順序選取樣本, 其有很大的可能會在相同的地方陷入局部困境, 或者收斂減緩. 因此, 欲使 SGD 發揮更好的效果, 應充分利用隨機化 [Randomise] 帶來的優勢: 可以在每次迭代之前 (偽代碼中最外圍循環), 對訓練集進行隨機排列.
因為每次只取一個樣本來進行梯度下降, SGD 的訓練速度很快, 但會引入噪聲, 使準確度下降. 這意味著并不是每次迭代都向著全局最優而去, 即并不是每次迭代都能使成本函數值降低. 不過換個思路的話, 噪聲在一定程度上以使算法避免了局部最優.
SGD 的另一個好處是, 可以使用在線學習 [online learning]. 也就是說, 在模型訓練好之后, 只要有新的數據到來, 模型都可以利用新的數據進行再學習, 更新參數,以適應新的變化.
MBGD
MBGD 是為解決 BGD 與 SGD 各自缺點而發明的折中算法, 或者說它利用了 BGD 和 SGD 各自優點. 其基本思想是: 每次更新參數時, 使用 n 個樣本, 既不是全部, 也不是 1. (SGD 可以看成是 n=1 的 MBGD 的一個特例)
此處就不再給出 MBGD 的成本函數或其求導公式或參數更新規則公式了, 基本同 BGD, 見上.
MBGD 的偽代碼如下:
- say b=10, m=1000,
- repeat {
- for i = 1, 11, 21, .., 991 {
- (for every j = 0, 1, .. n)
- }
- }
總結一下以上 3 個梯度下降算法的優缺點:
| 梯度下降算法 | 優點 | 缺點 |
|---|---|---|
| BGD | 全局最優解 | 計算量大, 迭代速度慢, 訓練速度慢 |
| SGD | 1.訓練速度快 2. 支持在線學習 |
準確度下降, 有噪聲, 非全局最優解 |
| MBGD | 1. 訓練速度較快, 取決于小批量的數目 2. 支持在線學習 |
準確度不如 BGD, 仍然有噪聲, 非全局最優解 |
Tips
下面將介紹一些梯度下降算法的使用技巧:
- 挑選合適的學習率 . 最好的選擇方法就是監測目標函數值 (本文中就是成本函數值) 隨時間的學習曲線.
- 繪制成本-時間的曲線, 觀察成本隨迭代的變化情況, 即梯度的變化情況. 若成本沒有隨著迭代而下降, 說明學習率過大了 (發散了).
- 學習率通常是一個很小的實值, 比如 0.1, 0.001, 0.0001. 學習率如果過大, 成本函數可能無法收斂, 一直處于發散狀態.
- 學習算法之前, 進行特征縮放能夠改善梯度下降. (親測! 原來使用較大學習率, 成本函數無法收斂; 使用特征縮放之后, 收斂了)
- 使用 MBGD 時, 在學習過程中, 可以逐漸增大小批量的大小, 更好地綜合發揮 BGD 與 SGD 的優勢.
進階
以下內容有點深奧, 筆者對一些概念也不甚熟悉, 僅僅是做個記錄
我注意到 Keras 實現的 SGD 提供了 3 個關鍵字參數: decay, momentum, nestrov:
- decay – 衰減的意思, 表示每一次迭代, 學習率 的衰減量.
- momentum – 動量的意思, 旨在加速學習, 稍后介紹.
- nesterov – 算法名, 表示是否使用 Nesterov 動量算法.
使用 BGD 達到極小值時, 整個成本函數的真實梯度會變得很小, 最終減小為 0, 因此 BGD 可以使用固定的學習率; 然而, SGD 中梯度估計引入的噪聲源不會在極小點處消失, 因此有必要隨著時間的推移逐漸降低學習率, 以保證 SGD 收斂.
實踐中, 一般讓學習率線性衰減, 直到第 次迭代:
其中, 表示第 k 次迭代, 表示第 次迭代, .
上式中, 需要設置的量包括: 初始學習率 , 最終學習率 以及 終止迭代次數 . 通常取幾百的大小, 則設為 的 . 因此, 剩下的主要問題就是選擇一個合適的 : 取值太大, 學習曲線會劇烈抖動, 成本會明顯增加; 取值太小, 學習過程會變得很緩慢.
上面提到, 在梯度下降中引入動量的概念, 是為了加速學習, 特別是對于處理高曲率 (曲率: 曲線偏離直線的程度), 小但一致的梯度, 或者帶噪聲的梯度, 有明顯的加速效果. 因為動量算法積累了之前梯度指數級衰減的移動平均 (移動平均: 分析時間序列數據的有效工具), 能夠繼續沿該方向移動, 從而使成本持續減小.
從形式上看, 動量算法引入了 充當速度的角色, 代表參數在參數空間移動的方向和速率. 被設為負梯度的指數衰減平均, 其更新規則如下:
從上式可以得出的一個結論是: 相對于 , 越大, 之前梯度對現在方向的影響就越大.
在引入動量的概念之前, 的更新步長只是梯度范數乘以學習率, 引入動量之后則取決于梯度序列的大小和排列. 當許多連續的梯度指向相同時, 步長最大
Nesterov 動量算法是標準動量算法的變種, 其更新規則如下:
Nesterov 動量算法與標準動量算法的區別在于梯度的計算, 其梯度計算是在施加了當前速度之后, 可以解釋為向標準動量方法中添加了一個校正因子.
題外話
研究優化算法的收斂率時, 一般會衡量額外誤差: , 即當前成本超出最低可能成本的量. SGD 應用于凸問題 (研究定義于凸集中的凸函數最小化的問題)時, k 步迭代的額外誤差量級是 , 在強凸情況下是 . 除非假定額外條件, 否則不能進一步改進.
Cramer-Rao 界限指出, 泛化誤差的下降速度不會快于 . Bottou and Bousquet 因此認為機器學習任務, 不值得探尋收斂快于 的優化算法, 因為:
更快的收斂可能對應過擬合
樣例代碼
以下是 BGD, SGD, MBGD 的 Python 代碼實現, 暫時不包括進階部分提到的高級內容.
- import numpy as np
- import pylab
- from sklearn.datasets.samples_generator import make_regression
- def bgd(alpha, x, y, numIterations):
- """Copied from Internet"""
- m = x.shape[0] # number of samples
- theta = np.ones(2)
- J_list = []
- x_transpose = x.transpose()
- for iter in range(0, numIterations):
- hypothesis = np.dot(x, theta)
- loss = y - hypothesis
- J = np.sum(loss ** 2) / (2 * m) # cost
- J_list.append(J)
- print("iter %s | J: %.3f" % (iter, J))
- gradient = np.dot(x_transpose, loss) / m
- theta += alpha * gradient # update
- pylab.plot(range(numIterations), J_list, "k-")
- return theta
- def sgd(alpha, x, y, num_iter):
- """Writtern by kissg"""
- m = x.shape[0] # number of samples
- theta = np.ones(2)
- J_list = []
- # 隨機化序列
- idx = np.random.permutation(y.shape[0])
- x, y = x[idx], y[idx]
- for j in range(num_iter):
- for i in idx:
- single_hypothesis = np.dot(x[i], theta)
- single_loss = y[i] - single_hypothesis
- gradient = np.dot(x[i].transpose(), single_loss)
- theta += alpha * gradient # update
- hypothesis = np.dot(x, theta)
- loss = y - hypothesis
- J = np.sum(loss ** 2) / (2 * m) # cost
- J_list.append(J)
- print("iter %s | J: %.3f" % (j, J))
- pylab.plot(range(num_iter), J_list, "r-")
- return theta
- def mbgd(alpha, x, y, num_iter, minibatches):
- """Writtern by kissg"""
- m = x.shape[0] # number of samples
- theta = np.ones(2)
- J_list = []
- for j in range(num_iter):
- idx = np.random.permutation(y.shape[0])
- x, y = x[idx], y[idx]
- mini = np.array_split(range(y.shape[0]), minibatches)
- for i in mini:
- mb_hypothesis = np.dot(x[i], theta)
- mb_loss = y[i] - mb_hypothesis
- gradient = np.dot(x[i].transpose(), mb_loss) / minibatches
- theta += alpha * gradient # update
- hypothesis = np.dot(x, theta)
- loss = y - hypothesis
- J = np.sum(loss ** 2) / (2 * m) # cost
- J_list.append(J)
- print("iter %s | J: %.3f" % (j, J))
- pylab.plot(range(num_iter), J_list, "y-")
- return theta
- if __name__ == '__main__':
- x, y = make_regression(n_samples=100, n_features=1, n_informative=1,
- random_state=0, noise=35)
- m, n = np.shape(x)
- x = np.c_[np.ones(m), x] # insert column, bias
- alpha = 0.01 # learning rate
- pylab.plot(x[:, 1], y, 'o')
- print("\n#***BGD***#\n")
- theta_bgd = bgd(alpha, x, y, 800)
- for i in range(x.shape[1]):
- y_bgd_predict = theta_bgd * x
- pylab.plot(x, y_bgd_predict, 'k--')
- print("\n#***SGD***#\n")
- theta_sgd = sgd(alpha, x, y, 10)
- for i in range(x.shape[1]):
- y_sgd_predict = theta_sgd * x
- pylab.plot(x, y_sgd_predict, 'r--')
- print("\n#***MBGD***#\n")
- theta_mbgd = mbgd(alpha, x, y, 50, 10)
- for i in range(x.shape[1]):
- y_mbgd_predict = theta_mbgd * x
- pylab.plot(x, y_mbgd_predict, 'y--')
- pylab.show()
- print("Done!")
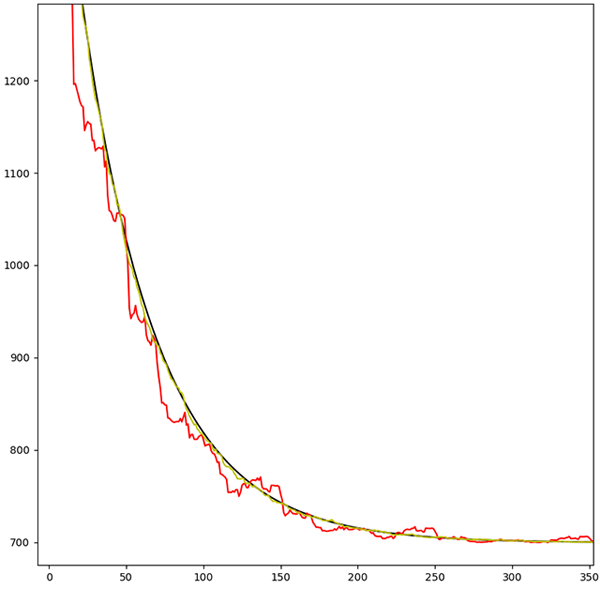
執行以上代碼, 得到 3 類梯度下降算法的函數圖像如下圖所示.
- 黑色是 BGD 的圖像, 是一條光滑的曲線, 因為 BGD 每一次迭代求得的都是全局最優解;
- 紅色是 SGD 的圖像, 可見抖動很劇烈, 有不少局部最優解;
- 黃色是 MBGD 的圖像, 相對 SGD 的成本-時間曲線平滑許多, 但仔細看, 仍然有抖動.