Java關于數據結構的實現:樹
文章目錄`
一 樹的概念與應用場景
1.1 二叉查找樹
1.2 AVL樹
1.3 紅黑樹
1.4 B樹
二 樹的操作與源碼實現
2.1 TreeMap/TreeSet實現原理
寫在前面
之前在網上看到過很多關于Java集合框架實現原理文章,但大都在講接口的作用與各類集合的實現,對其中數據結構的闡述的不多,例如紅黑樹的染色和旋轉是怎么進行的等等,本篇文章從 數據結構的基本原理出發,逐步去分析Java集合里數據結構的應用與實現。
一 樹的概念與應用場景
樹是一種抽象數據類型(ADT)或是實作這種抽象數據類型的數據結構,用來模擬具有樹狀結構性質的數據集合。它是由n(n>0)個有限節點組成一個具有層次關系的集合。把 它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
樹有以下特點:
每個節點有零個或多個子節點;
沒有父節點的節點稱為根節點;
每一個非根節點有且只有一個父節點;
除了根節點外,每個子節點可以分為多個不相交的子樹;
與樹相關的概念
節點的度:一個節點含有的子樹的個數稱為該節點的度;
樹的度:一棵樹中,最大的節點的度稱為樹的度;
葉節點或終端節點:度為零的節點;
非終端節點或分支節點:度不為零的節點;
父親節點或父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點;
孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點;
兄弟節點:具有相同父節點的節點互稱為兄弟節點;
節點的層次:從根開始定義起,根為第1層,根的子節點為第2層,以此類推;
深度:對于任意節點n, n的深度為從根到n的唯一路徑長,根的深度為0;
高度:對于任意節點n, n的高度為從n到一片樹葉的最長路徑長,所有樹葉的高度為0;
堂兄弟節點:父節點在同一層的節點互為堂兄弟;
節點的祖先:從根到該節點所經分支上的所有節點;
子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫。
森林:由m(m>=0)棵互不相交的樹的集合稱為森林;
注:參照親戚關系,這些概念很好理解,家族譜也是一種樹結構。:grinning:
樹的分類
無序樹:樹中任意節點的子節點之間沒有順序關系,這種樹稱為無序樹,也稱為自由樹;
有序樹:樹中任意節點的子節點之間有順序關系,這種樹稱為有序樹;
其中有序樹又分為:
二叉樹:每個節點最多含有兩個子樹的樹稱為二叉樹;
完全二叉樹:對于一顆二叉樹,假設其深度為d(d>1)。除了第d層外,其它各層的節點數目均已達最大值,且第d層所有節點從左向右連續地緊密排列,這樣的二叉樹被稱為完全二叉樹;
滿二叉樹:所有葉節點都在最底層的完全二叉樹;
AVL樹:當且僅當任何節點的兩棵子樹的高度差不大于1的二叉樹;
二叉查找樹:樹中的每個節點,它的左子樹中所有項小于X中的項,它的右子樹中的所有項大于X中的項。
霍夫曼樹:帶權路徑最短的二叉樹稱為哈夫曼樹或最優二叉樹;
B樹:一種對讀寫操作進行優化的自平衡的二叉查找樹,能夠保持數據有序,擁有多余兩個子樹。
1.1 二叉查找樹
二叉查找樹是一種有序二叉樹,它的查找、插入的時間復雜度為O(logN)
二叉查找是是一種有序二叉樹.
主要特點
若任意節點的左子樹不空,則左子樹上所有節點的值均小于它的根節點的值。
若任意節點的右子樹不空,則右子樹上所有節點的值均大于它的根節點的值。
任意節點的左右子樹葉為二叉查找樹
沒有鍵值相等的節點。
就就是說二叉查找樹上的節點是排好序的:左子樹 < 根節點 < 右子樹。
性能分析
在最壞的情況下,即當先后插入的關鍵字有序時,構造成的二叉查找樹蛻變為單支樹,輸的深度為n,其平均查找長度為(n+1)/2。
在最好的情況下,二叉查找樹的形態和折半查找的判定樹相同,其時間復雜度為O(log2(N))。
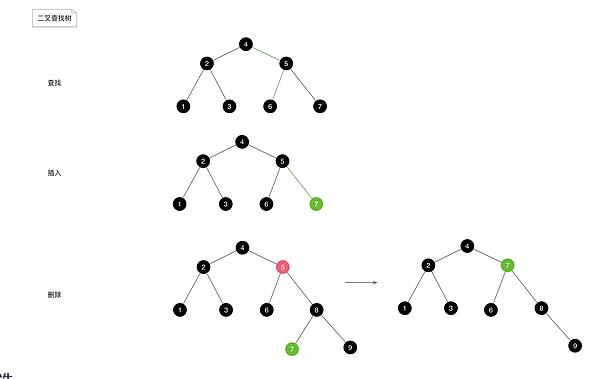
我們來看看二叉查找樹上的相關操作。
構造
當我們用一組數值構造一棵二叉查找樹時,就相當于對這組數值進行了排序,在最壞情況下,即該組數值是從小到達排好序的,構造出來的二叉樹的所有節點都 沒有左子樹,這種情況下的時間復雜度為O(N2)。(N的平方)
另外,樹排序的問題使得CPU Cache性能較差,特別是當節點是動態內存分配時。而堆排序的CPU Cache性能較好。另一方面,樹排序是最優的增量排序(incremental sorting)算法, 保持一個數值序列的有序性。
查找
由于二叉查找樹具有左子樹 < 根節點 < 右子樹的特點,因此在二叉查找樹b中查找x的過程如下:
若b是空樹,則查找失敗,否則:
若x等于根節點的值,則查找成功,否則:
若x小于b根節點的值,則查找左子樹,否則
若x大于b根節點的值,則查找右子樹。
整個流程是一個遞歸的過程。
插入
插入的過程也是查找的過程,在二叉查找樹中插入節點x的過程如下:
若b是空樹,則x作為根節點插入,否則:
若x的值等于根節點的值,則直接返回,否則:
若x的值小于根節點的值,則將x插入當該根節點的左子樹中,否則
將x插入該根節點的右子樹中。
這也是一個遞歸的過程,這里我們要關注兩點:
插入的過程也是查找的過程
二叉查找樹不允許有相同值的節點
刪除
在二叉查找樹上刪除一個節點,分為三種情況:
若刪除的是葉子節點,則不會破壞樹的結構,只需要修改其雙親節點的指針即可。
若刪除的節點只有一個孩子節點,則用它的孩子節點代替它的位置即可,如此也不會破壞紅黑樹的結構。
若刪除的節點有兩個孩子節點,這種情況復雜一下,我們通常會找到要刪除節點X的左子樹里的最大元素或者右子樹里的最小元素,然后用M替換掉X,再刪除節點,因為此時M最多只會有一個
節點(如果左子樹最大元素則沒有右子節點,若是右子樹最小元素則沒有左子節點),若M沒有孩子節點,直接進入情況1處理,若M只有一個孩子,則直接進入情況2處理。
另外,如果刪除的次數不多,可以采用 懶惰刪除 的方式,即當一個元素刪除時,它仍然留在樹中,只是被比較為已刪除,這種方式在有重復項是特別有用, 另外如果刪除的元素又重新插入,這種方式可以避免新單元的創建開銷。
1.2 AVL樹
AVL樹是帶有平衡條件的二叉查找樹。
主要特點
AVL樹中的任何階段的兩棵子樹高度最大差別為1.
AVL樹還有個平衡因子的概念,平衡因子 = 左子樹高度 - 右子樹高度,因此平衡因子為-1,0,1的為平衡二叉樹,其他的都是不平衡的。
另外,把一棵不平衡的二叉查找樹變成一棵平衡二叉樹,我們稱之為 AVL旋轉 。
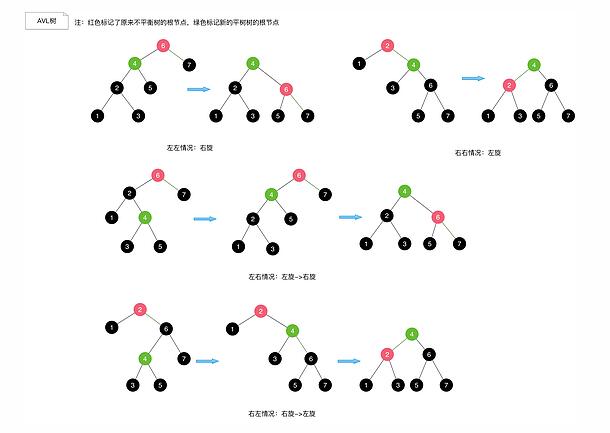
我們來看看不同情況下AVL旋轉如何進行。
左左情況:右旋
右右情況:左旋
左右情況:先左旋,再右旋
右左情況:先右旋,再左旋
注:所謂左左指的是左邊的左子樹多了一個,其他的依此類推。
具體操作如下所示,我們可以看到左左情況和右右情況只需要單旋轉就可以完成,左右情況與右左情況需要先把它們變成左左情況與右右情況 再進行旋轉,因此這兩種情況需要雙旋轉才能完成。
性能分析
查找、插入與刪除在平均和最壞的情況下的時間復雜度為O(logN)。
AVL樹也是二叉查找樹的一種,它的很多操作都可以向我們上面描述的二叉查找樹的操作那樣進行。刪除操作有點例外,我們在進行刪除操作
時可以把要刪除的節點向下旋轉形成一個葉子節點,然后直接刪除這個葉子節點,因為旋轉成葉子節點期間,做多有logN個節點被旋轉,每次 AVL旋轉花費的事件固定,所以刪除操作的時間復雜度是O(logN)。
1.3 紅黑樹
紅黑樹是平衡二叉樹的變種,它的操作的時間復雜度是O(logN).
紅黑樹是一種具有著色性質的樹,具有以下特點:
每個節點被著成紅色或者黑色
根是黑色的
葉子節點都是黑色的,葉子節點指的是NULL節點,有些紅黑樹圖中可能沒有標記出來。
如果一個節點是紅色的,那么他額子節點必須是黑色的,也就是不會存在兩個紅色節點毗鄰。
從一個節點到一個葉子節點(NULL節點)的每一條路徑必須包含相同數目的黑色節點。
紅黑樹也是一種二叉查找樹,查找操作與二叉查找樹相同,插入與刪除操作有所不同。
1.4 B樹
B樹是一種自平衡的樹,能夠保持數據有序,B樹為系統大塊數據的讀寫操作做了優化,通常用在數據庫與文件系統的實現上。
我們前面講解了二叉查找樹、AVL樹,紅黑樹,這三種都是典型的二叉查找樹結構,其查找的事件復雜度O(logN)與樹的深度有關,考慮這么一種情況,如果有 大量的數據,而節點存儲的數據有限,這種情況下,我們只能去擴充樹的深度,就會導致查找效率低下。
怎么解決這種問題,一個簡單的想法就是:二叉變多叉。
這里我們想象一下常見的文件系統,它也是一種樹結構,在查找文件時,樹的深度就決定了查找的效率。因此B樹就是為了減少數的深度從而提高查找效率的一種 數據結構。
主要特點
一個階為M的B樹具有以下特點:
注:M階指的是M叉查找樹,例如M = 2,則為二叉查找樹。
數據項存儲在樹葉上
非葉節點存儲直到M-1個關鍵字以指示搜索方向:關鍵字代表子樹i+1中最小的關鍵字
樹的根或者是一片樹葉,或者其兒子數都在2和M之間。
除根外,所有非樹葉節點的兒子樹在M/2與M之間。
所有的樹葉都在相同的深度上擁有的數據項都在L/2與L之間。
性能分析
B樹在查找、插入以及刪除等操作中,時間復雜度為O(logN)。
二 樹的操作與源碼實現
在文章 01Java關于數據結構的實現:表、棧與隊列 中我們 討論了ArrayList與LinkedList的實現,它們的瓶頸在于查找效率低下。因而Java集合設計了Set與Map接口,它們在插入、刪除與查找等基本操作都有良好的表現。
2.1 TreeMap/TreeSet實現原理
TreeSet實際上是基于TreeMap的NavigableSet的實現,它在功能上完全依賴于TreeMap,TreeMap是一個基于紅黑樹實現的Map,它在存儲時對元素進行排序。
因此只要理解了TreeMap實現即可,TreeSet在功能上完全依賴于TreeMap。
TreeMap具有以下特點:
TreeMap是一個有序的key-value集合,基于紅黑樹實現。
沒有實現同步
TreeMap實現以下接口:
NavigableMap:支持一系列導航方法,比如返回有序的key集合。
Cloneable:可以被克隆。
Serializable:支持序列化。
成員變量
//比較器
private final Comparator<? super K> comparator;
//根節點
private transient TreeMapEntry<K,V> root = null;
//集合大小
private transient int size = 0;
//修改次數
private transient int modCount = 0;
構造方法
public TreeMap() {
//默認比較器
comparator = null;
}
public TreeMap(Comparator<? super K> comparator) {
//指定比較器
this.comparator = comparator;
}
public TreeMap(Map<? extends K, ? extends V> m) {
//默認比較器
comparator = null;
putAll(m);
}
public TreeMap(SortedMap<K, ? extends V> m) {
//指定比較器
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
內部類
TreeMap里面定義了靜態內部類TreeMapEntry來描述節點信息。
static final class TreeMapEntry<K,V> implements Map.Entry<K,V> {
//鍵
K key;
//值
V value;
//指向左子樹的引用
TreeMapEntry<K,V> left = null;
//指向右子樹的引用
TreeMapEntry<K,V> right = null;
//指向父節點的引用
TreeMapEntry<K,V> parent;
//節點顏色,默認為黑色
boolean color = BLACK;
/**
* Make a new cell with given key, value, and parent, and with
* {@code null} child links, and BLACK color.
*/
TreeMapEntry(K key, V value, TreeMapEntry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* Returns the key.
*
* @return the key
*/
public K getKey() {
return key;
}
/**
* Returns the value associated with the key.
*
* @return the value associated with the key
*/
public V getValue() {
return value;
}
/**
* Replaces the value currently associated with the key with the given
* value.
*
* @return the value associated with the key before this method was
* called
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}
操作方法
在正式介紹TreeMap里的增、刪、改、查操作之前,我們先來看看TreeMop里關于節點染色,樹的旋轉等操作的實現,它們是TreeMap實現的基礎。
節點染色
在介紹染色規則之前,我們先來回顧一下紅黑樹的特點:
每個節點被著成紅色或者黑色
根是黑色的
葉子節點都是黑色的,葉子節點指的是NULL節點,有些紅黑樹圖中可能沒有標記出來。
如果一個節點是紅色的,那么他額子節點必須是黑色的,也就是不會存在兩個紅色節點毗鄰。
從一個節點到一個葉子節點(NULL節點)的每一條路徑必須包含相同數目的黑色節點。
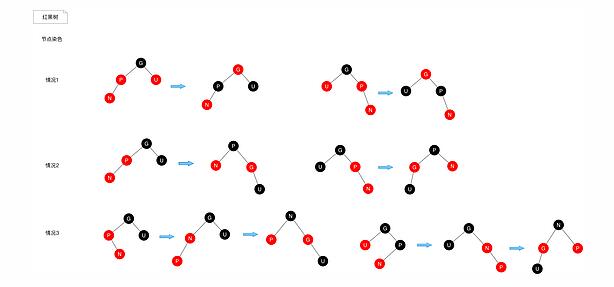
關于節點染色,我們有多種情況需要考慮。
首先說明
若新節點位于樹的根上,沒有父節點,直接將其染成黑色即可。這個在代碼中無需操作,因為節點默認就是黑色的。
若新節點的父節點是黑色,這個時候樹依然滿足紅黑樹的性質,并不需要額外的處理。
以上兩種情況無需額外的處理,我們再來考慮需要處理的情況。
情況1:如果新節點N的父節點P是紅色,且其叔父節點U也為紅色,我們可以將父節點P與叔父節點U染成黑色,祖父節點G染成紅色。
情況2:如果新節點N的父節點P是紅色,且其叔父節點U為黑色或者沒有叔父節點,P為其父節點P的右子節點,P為為其父節點G的左子節點。這種情況我們針對祖父節點G做一次右旋。并將P染成黑色,染成紅色
情況3:如果新節點N的父節點P是紅色,且其叔父節點U為黑色或者沒有叔父節點,P為其父節點P的右子節點,P為為其父節點G的左子節點。這種情況下我們對做一次左旋調換,調換P與N的位置,這樣情況3變成了 情況2,剩下的按照情況2處理即可。
我們來看看具體的源碼實現。
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable{
//染色
private void fixAfterInsertion(TreeMapEntry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
//新節點N(即x)在其祖父節點的左子樹上,叔父節點在左子樹上。
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
TreeMapEntry<K,V> y = rightOf(parentOf(parentOf(x)));
//情況1:如果新節點N的父節點P是紅色,且其叔父節點U也為紅色,我們可以將父節點P與叔父節點U染成黑色,祖父節點G染成紅色。
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//情況2:如果新節點N的父節點P是紅色,且其叔父節點U為黑色或者沒有叔父節點,P為其父節點P的右子節點,P為為其父節點G的左
//子節點。這種情況我們針對祖父節點G做一次右旋。并將P染成黑色,染成紅色
else {
//情況3:x為其父節點的右子節點,先對其父節點進行左旋,調換兩者的位置
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
}
//情況1:新節點N(即x)在其祖父節點的右子樹上,叔父節點在左子樹上,這種情況和在右子節點的情況相似,知識旋轉方向相反罷了。
else {
TreeMapEntry<K,V> y = leftOf(parentOf(parentOf(x)));
//如果新節點N的父節點P是紅色,且其叔父節點U也為紅色,我們可以將父節點P與叔父節點U染成黑色,祖父節點G染成紅色。
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
//情況2:如果新節點N的父節點P是紅色,且其叔父節點U為黑色或者沒有叔父節點,P為其父節點P的右子節點,P為為其父節點G的左
//子節點。這種情況我們針對祖父節點G做一次右旋。并將P染成黑色,染成紅色
else {
//情況3:x為其父節點的左子節點,先對其父節點進行右旋,調換兩者位置。
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
}
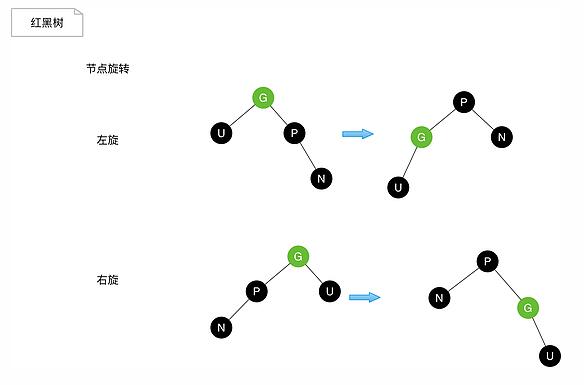
節點旋轉
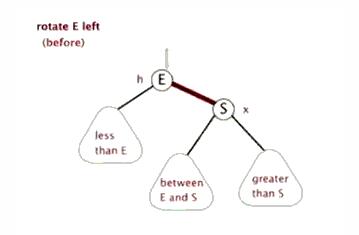
左旋
之前在網上看到一組關于左旋、右旋的動態圖,很形象,這里也貼出來。
找到要旋轉節點p的右節點r,然后將r的左子節點賦值給p的右子節點,如果r的左子節點為空,則直接將r節點設置為P的父節點。
將原來p的父節點設置成r的父節點,如果原來p的父節點為空,則直接接r設置成根節點,如果根節點不空且其做子節點為p,則將r設置為新的左子節點,如果根節點不空且其右子節點為p,則將r設置為新的右子節點,
再講r的左子節點設為p,p的父節點設置為r,左旋完成。
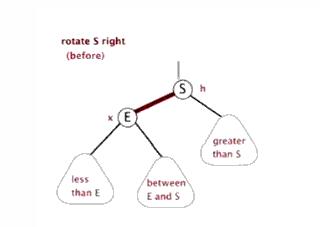
右旋
找到要旋轉節點p的左子節點l,然后將l的右子節點賦值給p的左子節點,如果l的右子節點為空,則直接將l節點設置為P的父節點。
將原來p的父節點設置成l的父節點,如果原來p的父節點為空,則直接接l設置成根節點,如果根節點不空且其做子節點為p,則將l設置為新的左子節點,如果根節點不空且其右子節點為p,則將l設置為新的右子節點,
再講l的右子節點設為p,p的父節點設置為l,右旋完成。
我們來看看具體的源碼實現。
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable{
//左旋
private void rotateLeft(TreeMapEntry<K,V> p) {
if (p != null) {
//找到要旋轉節點p的右節點r
TreeMapEntry<K,V> r = p.right;
//然后將r的左子節點賦值給p的右子節點
p.right = r.left;
//如果r的左子節點為空,則直接將r節點設置為P的父節點
if (r.left != null)
r.left.parent = p;
//將原來p的父節點設置成r的父節點
r.parent = p.parent;
//如果原來p的父節點為空,則直接接r設置成根節點
if (p.parent == null)
rroot = r;
//如果根節點不空且其做子節點為p,則將r設置為新的左子節點
else if (p.parent.left == p)
p.parent.left = r;
//如果根節點不空且其右子節點為p,則將r設置為新的右子節點
else
p.parent.right = r;
//再講r的左子節點設為p,p的父節點設置為r,左旋完成
r.left = p;
p.parent = r;
}
}
//右旋
private void rotateRight(TreeMapEntry<K,V> p) {
if (p != null) {
//找到要旋轉節點p的左子節點l
TreeMapEntry<K,V> l = p.left;
//然后將l的右子節點賦值給p的左子節點
p.left = l.right;
//如果l的右子節點為空,則直接將l節點設置為P的父節點
if (l.right != null) l.right.parent = p;
//將原來p的父節點設置成l的父節點
l.parent = p.parent;
//如果原來p的父節點為空,則直接接l設置成根節
if (p.parent == null)
root = l;
//如果根節點不空且其右子節點為p,則將l設置為新的右子節點
else if (p.parent.right == p)
p.parent.right = l;
//如果根節點不空且其做子節點為p,則將l設置為新的左子節點
else p.parent.left = l;
//再講l的右子節點設為p,p的父節點設置為l,右旋完成。
l.right = p;
p.parent = l;
}
}
}
put
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable{
public V put(K key, V value) {
//找到根節點
TreeMapEntry<K,V> t = root;
//如果根節點為空,則設置該元素為
if (t == null) {
if (comparator != null) {
if (key == null) {
comparator.compare(key, key);
}
} else {
if (key == null) {
throw new NullPointerException("key == null");
} else if (!(key instanceof Comparable)) {
throw new ClassCastException(
"Cannot cast" + key.getClass().getName() + " to Comparable.");
}
}
root = new TreeMapEntry<>(key, value, null);
//集合大小為1
size = 1;
//修改次數自增
modCount++;
return null;
}
int cmp;
TreeMapEntry<K,V> parent;
//獲取比較器
Comparator<? super K> cpr = comparator;
//如果比較器不空,則用指定的比較器進行比較
if (cpr != null) {
//循環遞歸,從根節點開始查找插入的位置,即查找的它的父節點,查找方式和我們上面講的二叉排序樹的查找方式相同
do {
parent = t;
cmp = cpr.compare(key, t.key);
//插入值小于當前節點,則繼續在左子樹上查詢
if (cmp < 0)
tt = t.left;
//插入值大于當前節點,則繼續在右子樹上查詢
else if (cmp > 0)
tt = t.right;
//如果相等,則替換當前的值
else
return t.setValue(value);
} while (t != null);
}
//如果比較器為坤寧宮,則使用默認的比較器
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
tt = t.left;
else if (cmp > 0)
tt = t.right;
else
return t.setValue(value);
} while (t != null);
}
//根據查找到的父節點,構造節點,并根據比結果將其插入到對應的位置
TreeMapEntry<K,V> e = new TreeMapEntry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
//給插入的節點染色
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
}
插入操作采用了二叉排序樹的查找算法,整個流程如下:
如果當前TreeMap沒有根節點,將當前節點作為根節點插入,否則,
根據提供的比較器(如果沒有提供則使用默認的比較器)進行查找比較,查找該節點的插入位置,即它的父節點的位置。
查找到父節點后,根據比較結果插入到對應位置,并進行染色處理。
remove
前面我們講了插入操作,刪除操作要比插入操作復雜一下,我們先來描述一下刪除操作的大概流程:
將紅黑樹當成一棵二叉查找樹,進行節點刪除。
通過旋轉和著色,使其重新變成一棵復合規則的紅黑樹。
二叉查找樹時怎么做刪除的。前面我們已經說過,在二叉查找樹上刪除一個節點,分為三種情況:
若刪除的是葉子節點,則不會破壞樹的結構,只需要修改其雙親節點的指針即可。
若刪除的節點只有一個孩子節點,則用它的孩子節點代替它的位置即可,如此也不會破壞紅黑樹的結構。
若刪除的節點有兩個孩子節點,這種情況復雜一下,我們通常會找到要刪除節點X的左子樹里的最大元素或者右子樹里的最小元素,然后用M替換掉X,再刪除節點,因為此時M最多只會有一個
節點(如果左子樹最大元素則沒有右子節點,若是右子樹最小元素則沒有左子節點),若M沒有孩子節點,直接進入情況1處理,若M只有一個孩子,則直接進入情況2處理。
注:這里的替換指的是值拷貝,值拷貝并不會破壞紅黑樹的性質。
這樣三種情況都可以當做第一種或者第二種情況處理。
在刪除節點時,我們有兩個問題需要注意:
如果刪除的額是紅色節點,不會違反紅黑樹的規則。
如果刪除的是黑色節點,那么這個路徑上就少了一個黑色節點,則違反了紅黑樹規則。
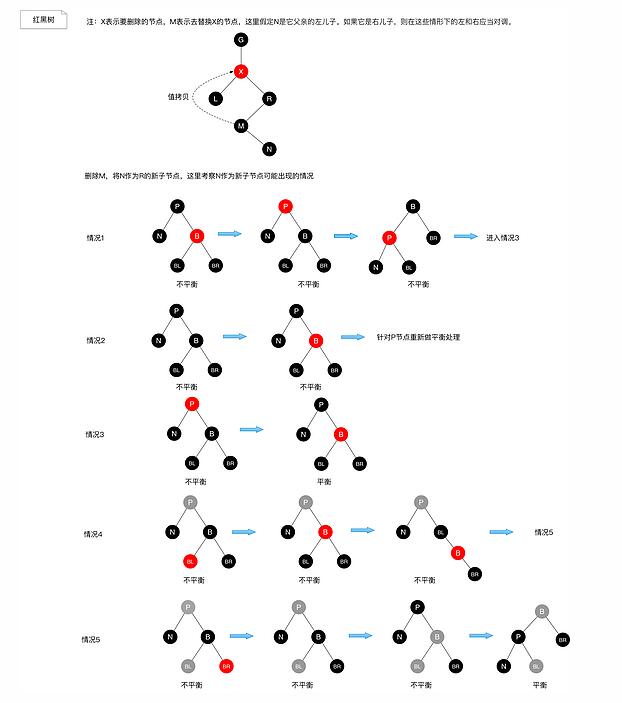
這樣我們可以得知只有在插入的節點是黑色的時候才需要我們進行處理,具體說來:
情況1:若刪除節點N的兄弟節點B是紅色,這種情況下,先對父節點P進行左旋操作,結合對換P與B的顏色。此時左子樹仍然少了一個黑色節點,此時進入情況3.
情況2:若刪除節點N的父親節點P,兄弟節點B以及B的兒子節點都是黑色,則將B染成紅色,這樣P到葉子節點的所有路徑都包含了相同的黑色節點,但是P的父節點G到葉子節點的路徑卻少了 一個黑色節點。這個時候我們要重新按照這套規則對P節點再進行一次平衡處理。
情況3:若刪除節點N的父親節點P是紅色,兄弟節點B是黑色,則交換P與B顏色,這樣在B所在路徑上增加了一個黑色節點,彌補了已經刪除的,樹重新達到平衡。
情況4: 若刪除節點N的兄弟節點B是黑澀,B的左孩子節點BL是紅色,B的右孩子節點BR是黑色,P為任意顏色。則減緩B與BL的顏色,右旋節點B。此時N所在路徑并沒有增加黑色節點,沒有達到平衡,進入情況5.
情況5:若刪除節點N的兄弟節點B是黑色,B的右孩子節點BR是紅色,B的左孩子節點BL為任意顏色,P為任意顏色。則BR染成黑色,P染成黑色,B染成原來P的顏色;左旋節點,這樣 N路徑上增加了一個黑色節點,B路徑上少了一個黑色節點B,又增加了一個黑色節點BR,剛好達到平衡。
以上的流程看起來比較復雜,本質上來說就是我們刪除了一個黑色節點,破壞了當前路徑黑色節點的個數,解決的方法要么為這條路徑再添加一個黑色節點,要么將其他路徑的黑色節點都去掉一個。
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable{
public V remove(Object key) {
TreeMapEntry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
private void deleteEntry(TreeMapEntry<K,V> p) {
//操作記錄自增
modCount++;
//集合大小自減
size--;
///如果要刪除的節點p的左右子節點都不為空,則查找其替代節點并進行節點替換
if (p.left != null && p.right != null) {
//查找其替代節點,替代節點為左子樹的最大元素或者右子樹的最小元素
TreeMapEntry<K,V> s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
} // p has 2 children
//查找替代節點的孩子節點,replacement指的是我們圖中說來的N節點,p指的是圖中的
TreeMapEntry<K,V> replacement = (p.left != null ? p.left : p.right);
//刪除p,并重新建立replacement節點的連接
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
pp.left = p.right = p.parent = null;
//如果刪除的黑色節點,則需要重新平衡樹
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
//查找其替代節點,替代節點為左子樹的最大元素或者右子樹的最小元素
static <K,V> TreeMapEntry<K,V> successor(TreeMapEntry<K,V> t) {
if (t == null)
return null;
//查找右子樹的最小元素,即最左孩子
else if (t.right != null) {
TreeMapEntry<K,V> p = t.right;
while (p.left != null)
pp = p.left;
return p;
}
//查找左子樹的最大元素,即最右孩子
else {
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
while (p != null && ch == p.right) {
ch = p;
pp = p.parent;
}
return p;
}
}
static <K,V> TreeMapEntry<K,V> predecessor(TreeMapEntry<K,V> t) {
if (t == null)
return null;
else if (t.left != null) {
TreeMapEntry<K,V> p = t.left;
while (p.right != null)
pp = p.right;
return p;
} else {
TreeMapEntry<K,V> p = t.parent;
TreeMapEntry<K,V> ch = t;
while (p != null && ch == p.left) {
ch = p;
pp = p.parent;s
}
return p;
}
}
}
我們再來看看deleteEntry()方法的實現流程:
如果要刪除的節點p的左右子節點都不為空,則查找其替代節點并進行節點替換。
查找替代節點的孩子節點,replacement指的是我們圖中說來的N節點,p指的是圖中的M,如果p是黑色節點,則刪除p后需要重新進行
樹的平衡處理。
get
public class TreeMap<K,V>
extends AbstractMap<K,V>
implements NavigableMap<K,V>, Cloneable, java.io.Serializable{
public V get(Object key) {
TreeMapEntry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
final TreeMapEntry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
TreeMapEntry<K,V> p = root;
//從根節點開始查找,根據比較結果決定從左子樹開始查找還是從右子樹開始查找
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
pp = p.left;
else if (cmp > 0)
pp = p.right;
else
return p;
}
return null;
}
}
TreeMap的查找流程和二叉查找樹的查找流程是一樣的,這里是從根節點開始查找,根據比較結果決定是下一步是從左子樹開始查找,還是從右子樹開始查找。