詳解數據結構二叉樹及其代碼實現
樹
樹是一種非常重要的非線性結構,本身具有遞歸的性質(在其后的編程中體現的淋漓盡致)。
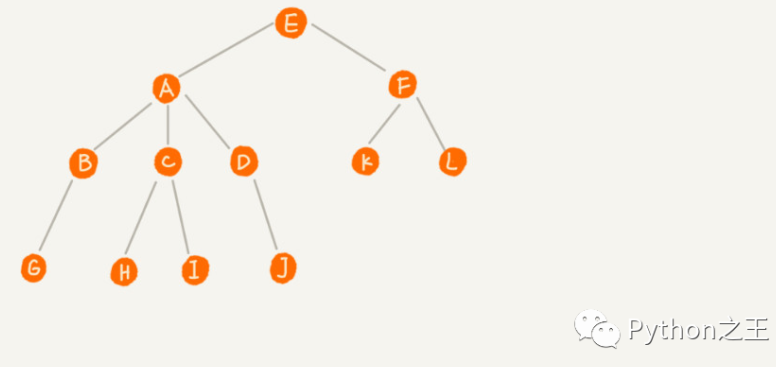
看下圖,A 節點就是 B 節點的父節點,B 節點是 A 節點的子節點。B、C、D 這三個節點的父節點是同一個節點A,沒有父節點的叫做根節點,也就是 E 。
沒有子節點的節點叫作葉子節點或者葉節點,圖中的G,H,I,J,K,L
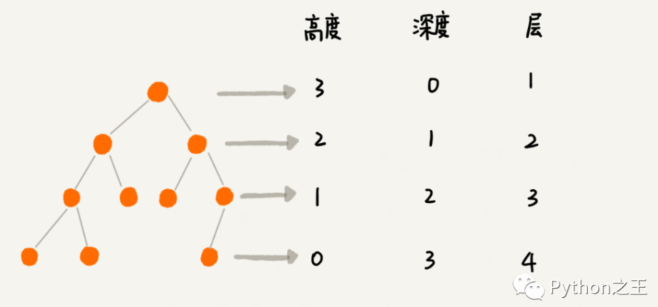
關于“樹”,還有三個比較相似的概念:高度(Height)、深度(Depth),層(level)
二叉樹(binary Tree)
二叉樹是n(n>=0)個結點的有限集合,該集合或者為空集(稱為空二叉樹),或者由一個根結點和兩棵互不相交的、分別稱為根結點的左子樹和右子樹組成。
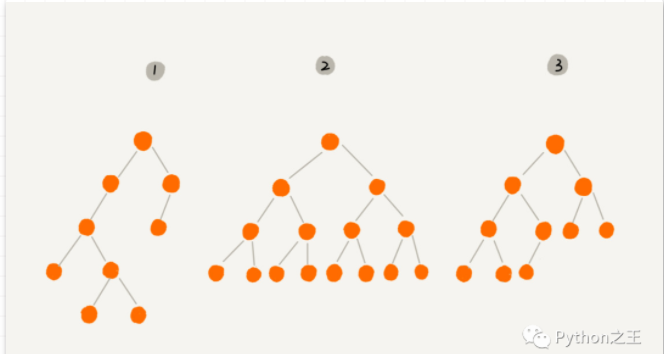
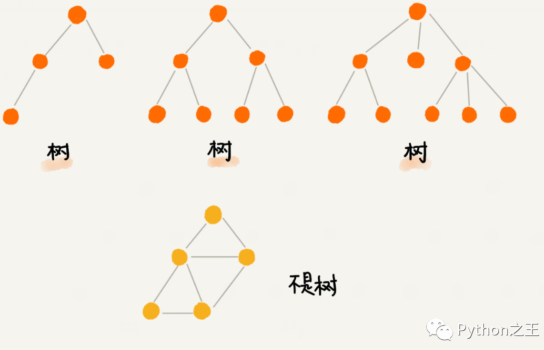
上圖中,編號1是普通二叉樹,編號2又是滿二叉樹,編號2又是完全二叉樹。
滿二叉樹:在一棵二叉樹中。如果所有分支結點都存在左子樹和右子樹,并且所有葉子都在同一層上,這樣的二叉樹稱為滿二叉樹。
滿二叉樹的特點有:
- 葉子只能出現在最下一層。出現在其它層就不可能達成平衡。
- 非葉子結點的度一定是2。
- 在同樣深度的二叉樹中,滿二叉樹的結點個數最多,葉子數最多。
編號3是完全二叉樹
「對一顆具有n個結點的二叉樹按層編號,如果編號為i(1<=i<=n)的結點與同樣深度的滿二叉樹中編號為i的結點在二叉樹中位置完全相同,則這棵二叉樹稱為完全二叉樹。」
就是保證葉子節點的上面層都要達到最大,最低下兩層,最后一層的葉子節點都靠左排列
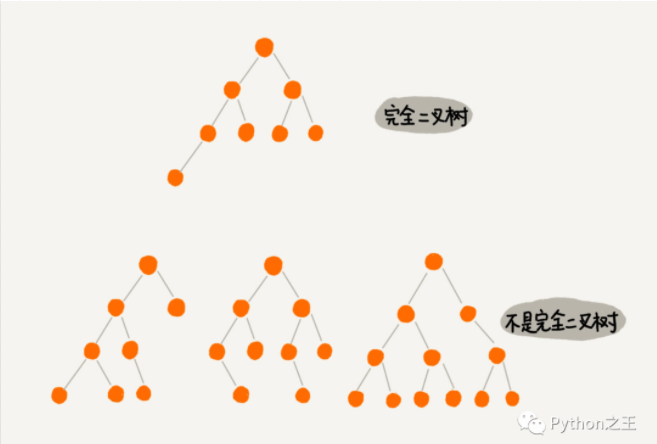
二叉樹具備以下數學性質:
在二叉樹的第i層上至多有2(i-1)個結點(i>0)
深度為k的二叉樹至多有2K-1個結點(k>0)
對于任意一棵二叉樹,如果其葉結點數為N0,而度數為2的結點總數為N2,則N0=N2+1;
具有n個結點的完全二叉樹的深度必為log2(n+1)
二叉樹的遍歷和節點的刪除
二叉樹的遍歷是指從二叉樹的根結點出發,按照某種次序依次訪問二叉樹中的所有結點,使得每個結點被訪問一次,且僅被訪問一次。
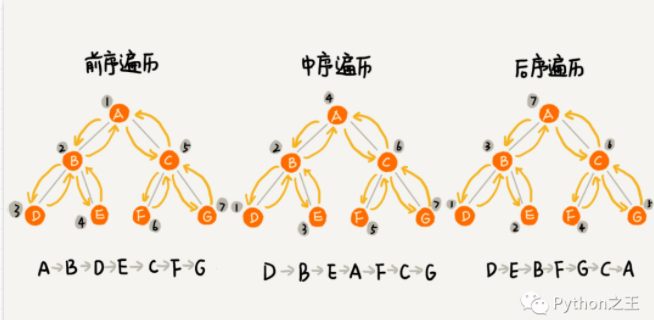
- 中序遍歷:先左子樹,再根節點,最后右子樹
- 前序遍歷:先根節點,再左子樹,最后右子樹
- 后序遍歷:先左子樹,再右子樹,最后根節點。
前序遍歷通俗的說就是從二叉樹的根結點出發,當第一次到達結點時就輸出結點數據,按照先向左在向右的方向訪問。
中序遍歷就是從二叉樹的根結點出發,當第二次到達結點時就輸出結點數據,按照先向左在向右的方向訪問。
后序遍歷就是從二叉樹的根結點出發,當第三次到達結點時就輸出結點數據,按照先向左在向右的方向訪問。
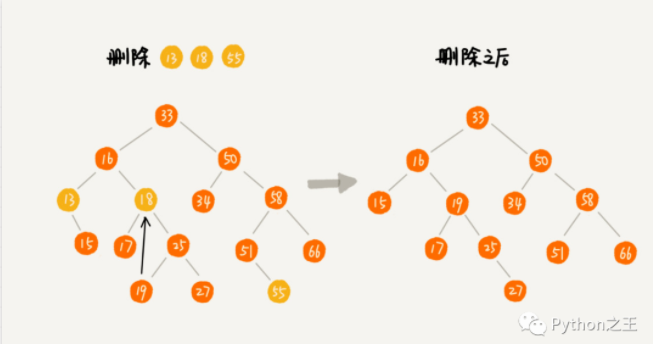
刪除共有三種情況
- 被刪除的節點是葉子節點,這時候只要把這個節點刪除,再把指向這個節點的父節點指針置為空就行
- 被刪除的節點有左子樹,或者有右子樹,而且只有其中一個,那么只要把當前刪除節點的父節點指向被刪除節點的左子樹或者右子樹就行。
- 如果要刪除的節點有兩個子節點,需要找到這個節點的右子樹的最小節點,把它替換到要刪除的節點上,然后再刪除掉這個最小節點,因為最小節點肯定沒有左子節點
代碼具體實現二叉樹
上面就是二叉樹全部內容,下面用Pytho代碼具體實現二叉樹。
按下來就是編程實現了,請動手自己實現一把。
先實現一個 node 節點類:
- class Node(object):
- def __init__(self, item):
- self.item = item
- self.left = None
- self.right = None
- def __str__(self):
- return str(self.item)
這里的 __str__ 方法是為了方便打印。在 print 一個 Node 類時會打印__str__的返回值,例如:print(Node(5)) 就會打印出字符串 5 。
實現一個二叉樹類:
- class Tree(object):
- def __init__(self):
- # 根節點定義為 root 永不刪除,做為哨兵使用。
- self.root = Node('root')
- # 添加節點操作
- def add(self, item):
- node = Node(item)
- if self.root is None:
- self.root = node
- else:
- q = [self.root]
- while True:
- pop_node = q.pop(0)
- if pop_node.left is None:
- pop_node.left = node
- return
- elif pop_node.right is None:
- pop_node.right = node
- return
- else:
- q.append(pop_node.left)
- q.append(pop_node.right)
- def get_parent(self, item):
- '''
- 找到 Item 的父節點
- '''
- if self.root.item == item:
- return None # 根節點沒有父節點
- tmp = [self.root]
- while tmp:
- pop_node = tmp.pop(0)
- if pop_node.left and pop_node.left.item == item:
- return pop_node
- if pop_node.right and pop_node.right.item == item:
- return pop_node
- if pop_node.left is not None:
- tmp.append(pop_node.left)
- if pop_node.right is not None:
- tmp.append(pop_node.right)
- return None
- def delete(self, item):
- '''
- 從二叉樹中刪除一個元素
- 先獲取 待刪除節點 item 的父節點
- 如果父節點不為空,
- 判斷 item 的左右子樹
- 如果左子樹為空,那么判斷 item 是父節點的左孩子,還是右孩子,如果是左孩子,將父節點的左指針指向 item 的右子樹,反之將父節點的右指針指向 item 的右子樹
- 如果右子樹為空,那么判斷 item 是父節點的左孩子,還是右孩子,如果是左孩子,將父節點的左指針指向 item 的左子樹,反之將父節點的右指針指向 item 的左子樹
- 如果左右子樹均不為空,尋找右子樹中的最左葉子節點 x ,將 x 替代要刪除的節點。
- 刪除成功,返回 True
- 刪除失敗, 返回 False
- '''
- if self.root is None: # 如果根為空,就什么也不做
- return False
- parent = self.get_parent(item)
- if parent:
- del_node = parent.left if parent.left.item == item else parent.right # 待刪除節點
- if del_node.left is None:
- if parent.left.item == item:
- parent.left = del_node.right
- else:
- parent.right = del_node.right
- del del_node
- return True
- elif del_node.right is None:
- if parent.left.item == item:
- parent.left = del_node.left
- else:
- parent.right = del_node.left
- del del_node
- return True
- else: # 左右子樹都不為空
- tmp_pre = del_node
- tmp_next = del_node.right
- if tmp_next.left is None:
- # 替代
- tmp_pre.right = tmp_next.right
- tmp_next.left = del_node.left
- tmp_next.right = del_node.right
- else:
- while tmp_next.left: # 讓tmp指向右子樹的最后一個葉子
- tmp_pre = tmp_next
- tmp_next = tmp_next.left
- # 替代
- tmp_pre.left = tmp_next.right
- tmp_next.left = del_node.left
- tmp_next.right = del_node.right
- if parent.left.item == item:
- parent.left = tmp_next
- else:
- parent.right = tmp_next
- del del_node
- return True
- else:
- return False
- def traverse(self): # 層次遍歷
- if self.root is None:
- return None
- q = [self.root]
- res = [self.root.item]
- while q != []:
- pop_node = q.pop(0)
- if pop_node.left is not None:
- q.append(pop_node.left)
- res.append(pop_node.left.item)
- if pop_node.right is not None:
- q.append(pop_node.right)
- res.append(pop_node.right.item)
- return res
- def preorder(self, root): # 先序遍歷
- if root is None:
- return []
- result = [root.item]
- left_item = self.preorder(root.left)
- right_item = self.preorder(root.right)
- return result + left_item + right_item
- def inorder(self, root): # 中序遍歷
- if root is None:
- return []
- result = [root.item]
- left_item = self.inorder(root.left)
- right_item = self.inorder(root.right)
- return left_item + result + right_item
- def postorder(self, root): # 后序遍歷
- if root is None:
- return []
- result = [root.item]
- left_item = self.postorder(root.left)
- right_item = self.postorder(root.right)
- return left_item + right_item + result
運行測試:
- if __name__ == '__main__':
- t = Tree()
- for i in range(10):
- t.add(i)
- print('層序遍歷:', t.traverse())
- print('先序遍歷:', t.preorder(t.root))
- print('中序遍歷:', t.inorder(t.root))
- print('后序遍歷:', t.postorder(t.root))
- for i in range(10):
- print(i, " 的父親", t.get_parent(i))
- for i in range(0, 15, 3):
- print(f"刪除 {i}", '成功' if t.delete(i) else '失敗')
- print('層序遍歷:', t.traverse())
- print('先序遍歷:', t.preorder(t.root))
- print('中序遍歷:', t.inorder(t.root))
- print('后序遍歷:', t.postorder(t.root))
執行結果如下:
- 層序遍歷: ['root', 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
- 先序遍歷: ['root', 0, 2, 6, 7, 3, 8, 9, 1, 4, 5]
- 中序遍歷: [6, 2, 7, 0, 8, 3, 9, 'root', 4, 1, 5]
- 后序遍歷: [6, 7, 2, 8, 9, 3, 0, 4, 5, 1, 'root']
- 0 的父親 root
- 1 的父親 root
- 2 的父親 0
- 3 的父親 0
- 4 的父親 1
- 5 的父親 1
- 6 的父親 2
- 7 的父親 2
- 8 的父親 3
- 9 的父親 3
- 刪除 0 成功
- 層序遍歷: ['root', 8, 1, 2, 3, 4, 5, 6, 7, 9]
- 先序遍歷: ['root', 8, 2, 6, 7, 3, 9, 1, 4, 5]
- 中序遍歷: [6, 2, 7, 8, 3, 9, 'root', 4, 1, 5]
- 后序遍歷: [6, 7, 2, 9, 3, 8, 4, 5, 1, 'root']
- 刪除 3 成功
- 層序遍歷: ['root', 8, 1, 2, 9, 4, 5, 6, 7]
- 先序遍歷: ['root', 8, 2, 6, 7, 9, 1, 4, 5]
- 中序遍歷: [6, 2, 7, 8, 9, 'root', 4, 1, 5]
- 后序遍歷: [6, 7, 2, 9, 8, 4, 5, 1, 'root']
- 刪除 6 成功
- 層序遍歷: ['root', 8, 1, 2, 9, 4, 5, 7]
- 先序遍歷: ['root', 8, 2, 7, 9, 1, 4, 5]
- 中序遍歷: [2, 7, 8, 9, 'root', 4, 1, 5]
- 后序遍歷: [7, 2, 9, 8, 4, 5, 1, 'root']
- 刪除 9 成功
- 層序遍歷: ['root', 8, 1, 2, 4, 5, 7]
- 先序遍歷: ['root', 8, 2, 7, 1, 4, 5]
- 中序遍歷: [2, 7, 8, 'root', 4, 1, 5]
- 后序遍歷: [7, 2, 8, 4, 5, 1, 'root']
- 刪除 12 失敗
- 層序遍歷: ['root', 8, 1, 2, 4, 5, 7]
- 先序遍歷: ['root', 8, 2, 7, 1, 4, 5]
- 中序遍歷: [2, 7, 8, 'root', 4, 1, 5]
- 后序遍歷: [7, 2, 8, 4, 5, 1, 'root']
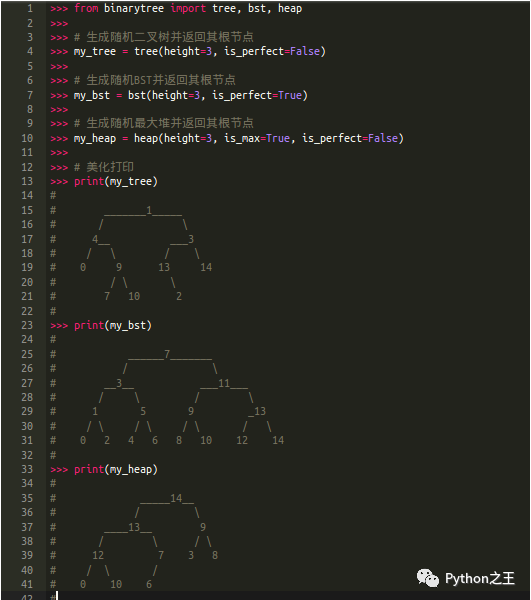
Binarytree是一個Python庫,它通過一個簡單的API生成二叉樹,可以進行檢查和操作。Github:https://github.com/joowani/binarytree/releases。
本文已收錄 GitHub https://github.com/MaoliRUNsen/runsenlearnpy100